跨坐式單軌彈性車體和轉向架耦合振動分析

成金娜，周勁松，王超冉

(同濟大學鐵道與城市軌道交通研究院，上海 201804)

跨坐式單軌具有造價低、彎道半徑小及車輛運行噪聲低等特點，已廣泛應用于國內外許多城市。對跨坐式單軌車輛車體進行輕量化設計，在降低車體承載結構質量的同時，導致車體剛度大幅下降。車體剛度過低會導致車體垂向彎曲，可能會引起車體與轉向架產生共振。隨著車體輕量化，在進行車輛穩定性和舒適性分析時必須考慮部件的彈性，這也成為國內外學者近年來研究的熱點。宮島等[1]對高速列車彈性車體和轉向架耦合振動進行了分析；李麗和王瑞卿等[2-3]建立了剛柔耦合動力學模型，對地鐵車輛的耦合振動進行了分析。也有一些學者研究了如何抑制車體彈性振動，宮島[4]、周勁松等[5～6]通過加裝吸振器、采用最優控制以及被動控制的方法，較好地抑制了車體一階彎曲模態的結構振動；黃彩虹等[7]研究了牽引拉桿縱向剛度對高速客車車體彈性振動的影響。以上研究針對的均是鐵道車輛彈性車體，尚未有學者對跨坐式單軌彈性車體和轉向架的耦合振動進行研究。跨坐式單軌采用膠輪走行，為改善彎道通過性能，部分車型采用單軸轉向架，其轉向架點頭和浮沉運動較為明顯。基于上述調研，本文建立了車體彈性振動的剛柔耦合系統動力學模型，研究了車體低階振動與轉向架耦合振動對車輛運行平穩性的影響，分析了彈性車體與轉向架的垂向耦合振動，探究跨坐式單軌車輛彈性共振的原因。

1 車輛運行平穩性指標

本文采用Sperling指標評價跨坐式單軌車輛的運行平穩性。根據GB/T 5599—1985標準，運行平穩性Sperling指標的計算式為：

(1)

式中：W為平穩性指標；A為振動加速度，g；f為振動頻率，Hz；F(f)為頻率修正系數。

根據平穩性指標確定車輛運行平穩性的等級，具體見表1，垂向和橫向采用相同的評定等級。

表1 客車Sperling運行平穩性指標

2 車輛系統模型

為了建立車體剛柔耦合動力學模型，運用HyperWorks建立車體有限元模型，計算生成包含車體結構及模態信息的fem文件，并將該文件通過相關接口導入動力學軟件Simpack中，完成彈性車體-剛性轉向架的剛柔耦合多體動力學模型的建立。

2.1 彈性車體縮聚

針對某跨坐式單軌拖車車體，運用有限元軟件Hypermesh劃分其模型網格，進行模態計算(如圖1)，然后將計算結果導入動力學軟件Simpack中。為了減少剛柔耦合系統運算量，同時盡可能保留原彈性車體信息，需要對彈性車體進行縮聚。Guyan[8]提出了在靜態結構分析中可以對研究對象的剛度矩陣進行縮減的理論，通過矩陣運算保留系統的主要自由度，消除[9]影響小的從自由度，從而減少計算量。縮聚是將彈性車體看作有限元模型節點的集合，列出節點坐標方程、動能矩陣T、勢能矩陣W及能量耗散矩陣Γ，應用拉格朗日方法得到該節點的動力學方程，通過矩陣組裝法得到整個彈性體的動力學方程：

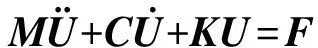
(2)

式中：U為節點狀態向量；F為載荷矩陣;M為質量矩陣；C為阻尼矩陣；K為剛度矩陣。

圖1 跨坐式單軌車體模態圖

車體縮聚后的模型如圖2所示，圖中的圓點是縮聚選用的重要節點。Guyan縮聚法可保留原模型車體的大部分信息，尤其是彈性變形信息。為了校核模型的準確性，對縮聚前后的模型進行模態對比分析，見表2。與車體平穩性關系最大的典型模態是垂向一階彎曲，由縮聚前后車體主要典型模態值可以看出，縮聚計算前后，典型振型的模態頻率相差較小，垂向一階彎曲模態頻率基本一致(誤差僅為0.43%)，表明縮聚后的模型是準確的。

圖2 車體縮聚后的模型

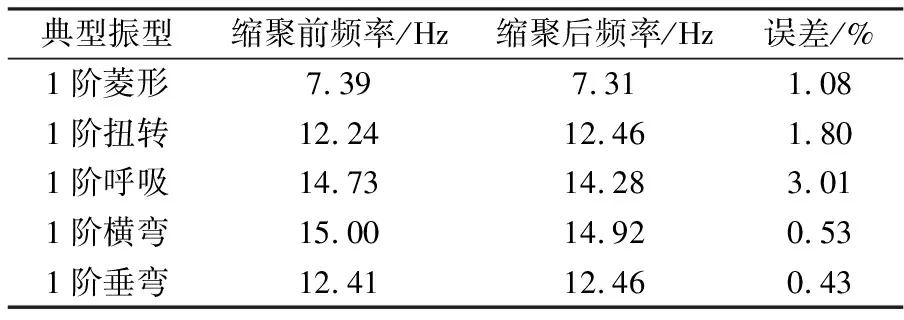
典型振型縮聚前頻率/Hz縮聚后頻率/Hz誤差/%1階菱形7.397.311.081階扭轉12.2412.461.801階呼吸14.7314.283.011階橫彎15.0014.920.531階垂彎12.4112.460.43

2.2 車輛動力學建模

跨坐式單軌單節車輛的剛柔耦合動力學模型如圖3所示，包括1個車體、2個構架、8個走行輪、8個導向輪和4個穩定輪剛體。與車體相比構架彈性變形相對較小，因此考慮將其視為剛性；空氣彈簧的垂向、橫向和縱向剛度簡化為線性彈簧，走行輪和水平輪視為各向同性的線性彈簧，抗點頭裝置等效為轉向架和車體之間的扭轉彈簧，布置在轉向架兩側。在模型中考慮以下非線性因素：彈性止檔剛度、垂向液壓減振器阻尼系數等。根據GB/T 5599—1985標準，在Simpack后處理中設置車體振動測點Sensor1和Sensor2，分別布置在轉向架中心左右1m處(對應車體坐標系坐標分別為(6,1,0.5)、(-6,-1,0.5))。

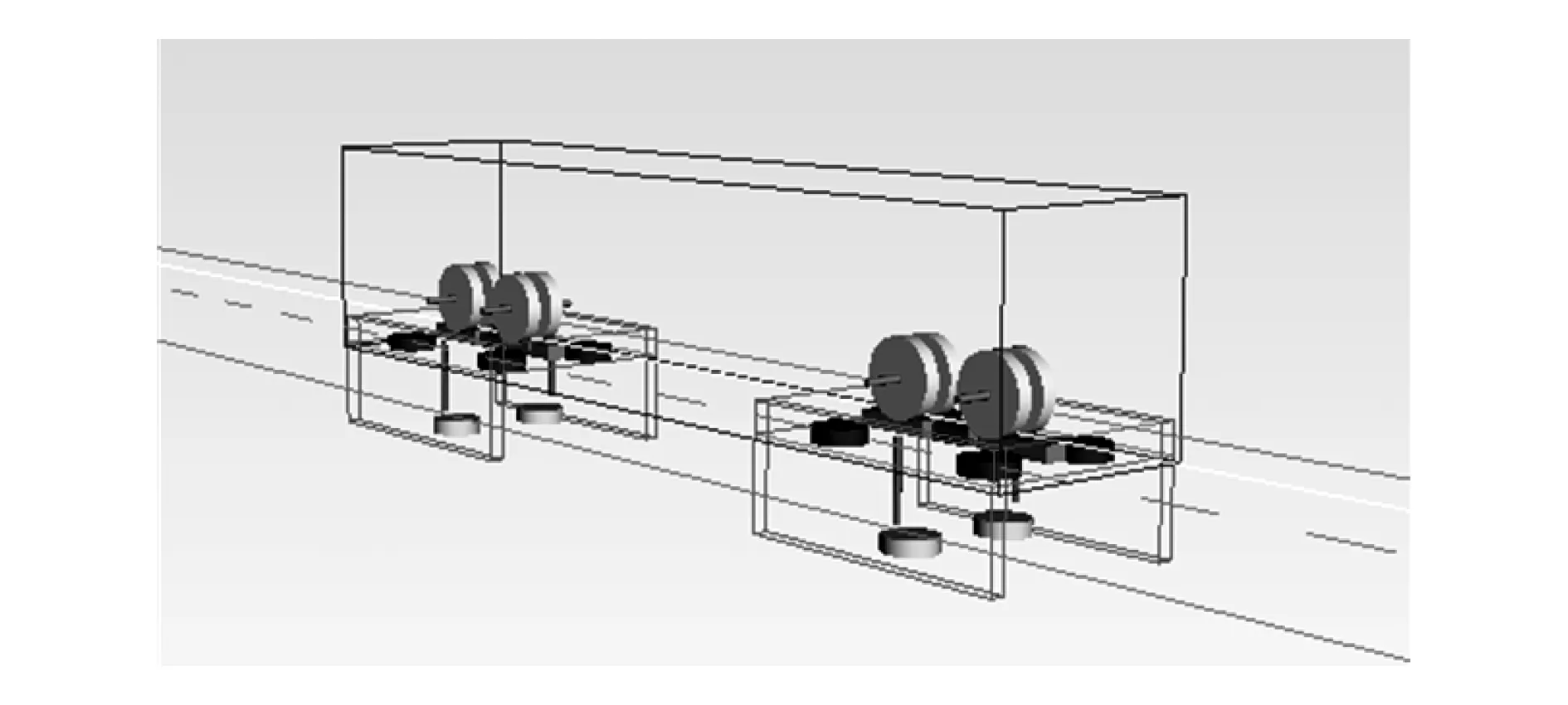
圖3 單軌車輛動力學模型

3 彈性車體對運行平穩性的影響

軌道激勵采用ISO8608標準A級公路譜，系數取為0.5。基于剛柔耦合動力學模型，通過仿真分析車輛在不同運行速度下彈性車體和剛性車體的垂向振動加速度(圖4)和運行平穩性，根據式(1)求出車體垂向和橫向運行平穩性Sperling指標，如圖5所示。

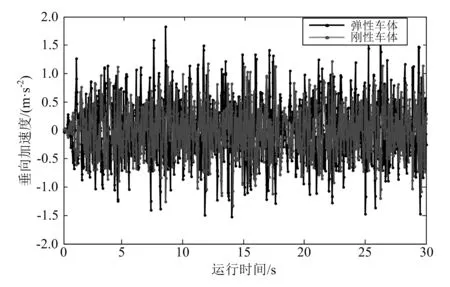
圖4 車體垂向振動加速度

分析可知：相同工況下，彈性車體的振動加速度大于剛性車體的振動加速度；相同速度下，彈性車體的垂向和橫向Sperling指標大于剛性車體，即剛性車體運行平穩性優于彈性車體；剛性車體和彈性車體的運行平穩性均隨著速度的增加而減小，但在單軌最高限速90km/h內均滿足運營要求，平穩性等級為“優”；彈性車體的平穩性曲線波動較大。因此，在尋求車體輕量化的同時，不可過分強調降低車體質量，以免車體剛度太小，運行平穩性變差。

圖5 不同運行速度下車輛運行平穩性

4 轉向架與彈性車體垂向耦合振動分析

車體的彈性振動主要由轉向架振動經二系懸掛裝置傳遞產生，要確保車體運行的垂向動力學性能，必須考慮轉向架與彈性車體的垂向耦合振動的運行特性，此時需要分析轉向架浮沉與點頭頻率隨一系懸掛垂向剛度變化的情況，研究轉向架浮沉及點頭頻率對彈性車體運行平穩性的影響。因跨坐式單軌車體軸距較小或為單軸設計，轉向架的點頭和浮沉運動較鐵道車輛更為明顯，因此研究轉向架浮沉及點頭頻率對彈性車體運行平穩性的影響至關重要。單軌轉向架須安裝抗點頭裝置，抑制構架的點頭運動。抗點頭裝置的剛度對前后轉向架同相和異相點頭振動的影響如圖6所示。隨著抗點頭裝置剛度的增加，轉向架的點頭頻率呈線性增大，阻尼比呈減小趨勢；前后轉向架同相點頭時的頻率大于異相點頭頻率，阻尼比呈大致相反趨勢。

基于車輛剛柔耦合系統動力學模型，仿真分析在不同構架點頭頻率下車體的運行平穩性變化，如圖7所示。

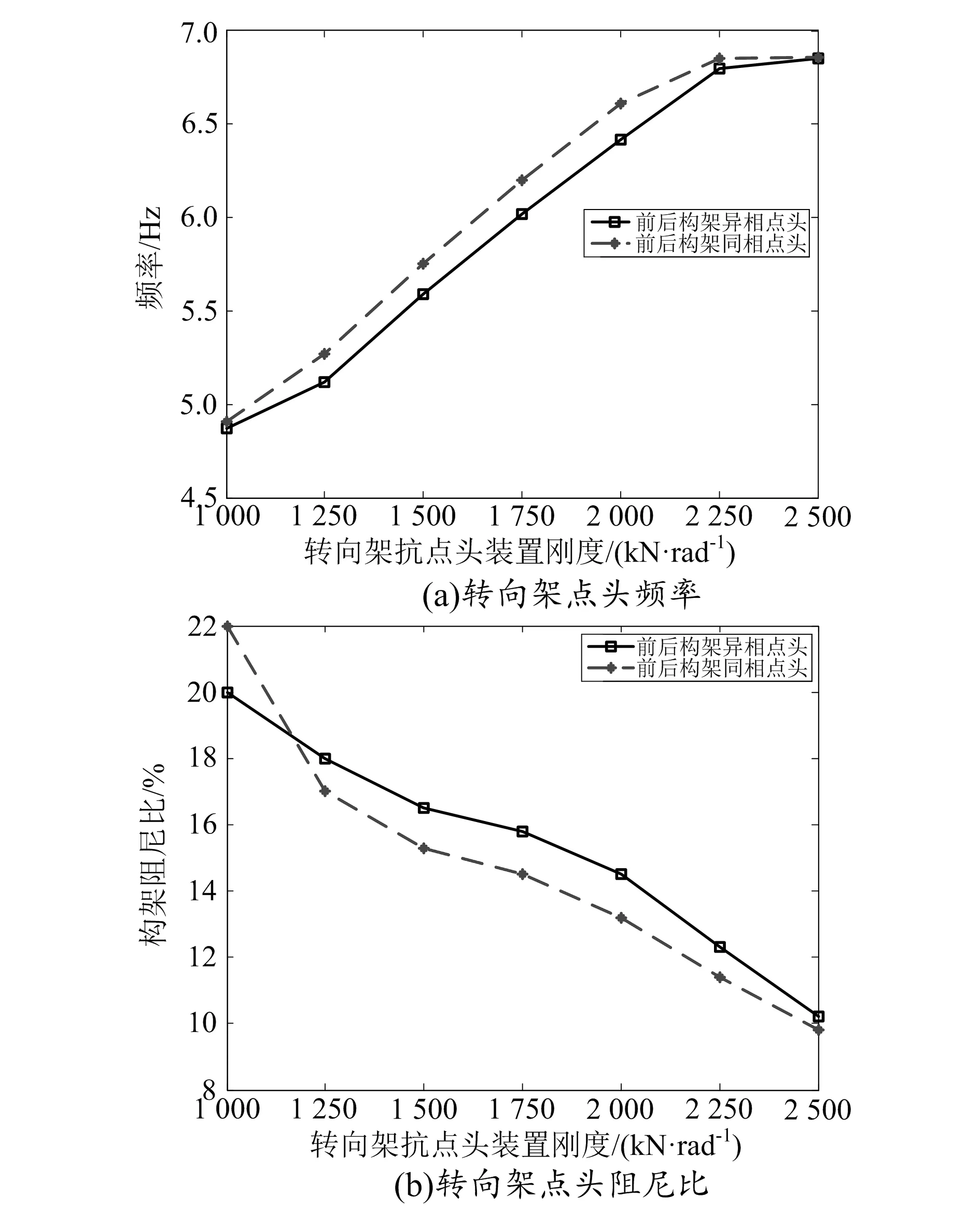
圖6 前后轉向架點頭頻率及阻尼比

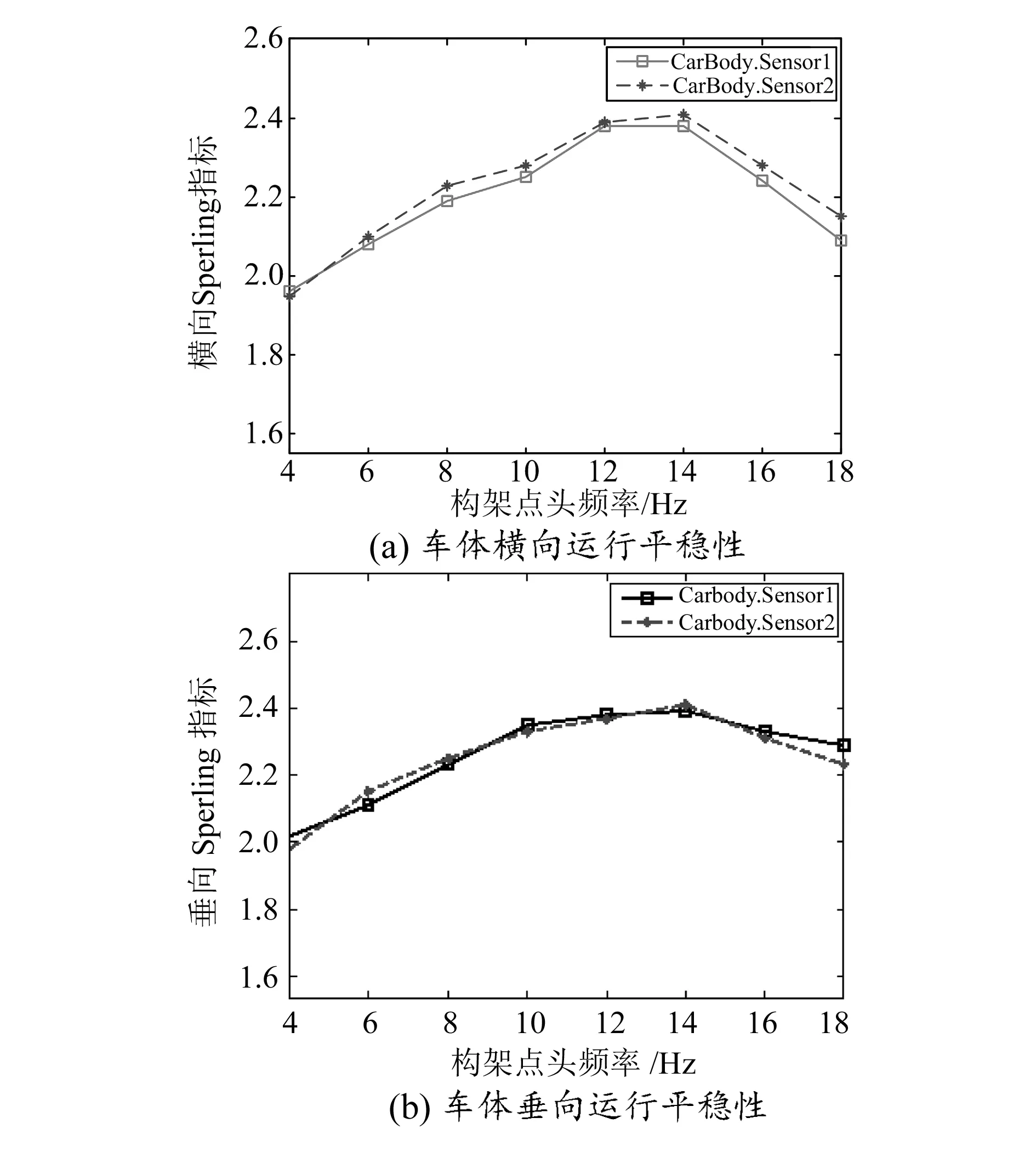
圖7 不同構架點頭頻率下車體運行平穩性

由圖7可知，轉向架和彈性車體的耦合振動對車輛運行平穩性產生了不利影響。隨著轉向架點頭頻率(4～18Hz)的增加，垂向和橫向平穩性的變化曲線均呈拋物線型，在轉向架點頭頻率為12～14Hz時Sperling指數值達到最大，但最大值小于2.5，等級為“優”。 彈性車體模態計算中得到車體一階垂彎頻率為12.4Hz，此時轉向架和彈性車體的耦合振動最為劇烈，車輛平穩性最低，但由于車輛懸掛系統參數的合理配置和阻尼力共同作用的效果，并未發生共振現象。空氣彈簧和減振器安裝在車體和構架間，是二系垂向懸掛裝置，其作用是支撐車體和衰減振動。當轉向架振動頻率與車體的一階垂彎頻率一致時，垂向減振器阻尼系數和空氣彈簧垂向剛度對車輛平穩性的影響如圖8、圖9所示。從圖中可以看出，隨著減振器阻尼系數增大，車輛平穩性迅速改善后又緩慢變差，阻尼系數在6 000N/(m·s-1)時車輛平穩性達到最優；車體平穩性隨著空氣彈簧剛度的減小而變好，即空氣彈簧越“軟”，車輛的平穩性越好。

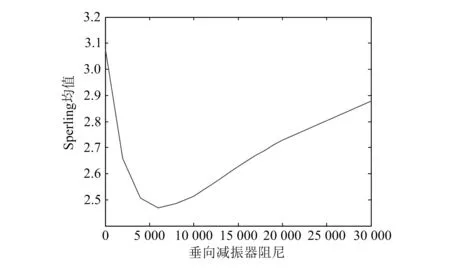
圖8 減振器阻尼值的影響

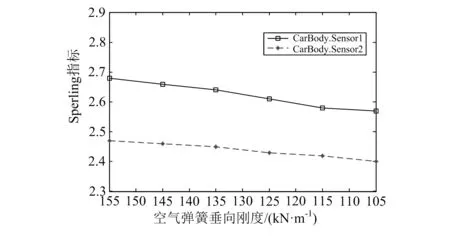
圖9 空氣彈簧剛度的影響

5 結論

本文對跨座式單軌彈性車體與轉向架的耦合振動進行分析，得出以下結論：

1)相同運行速度下彈性車體比剛性車體運行平穩性差，波動更明顯；隨著速度增加，運行平穩性指標單調遞增。

2)對于單軌車體車輛，隨抗點頭裝置剛度的增加，轉向架的點頭頻率呈線性增大，阻尼比呈減小趨勢；前后轉向架同相點頭時的頻率大于異相點頭頻率，阻尼比呈大致相反趨勢。

3)只要跨座式單軌抗點頭扭桿剛度、減振器阻尼系數和空氣彈簧剛度與車體一階彎曲頻率匹配恰當，即使轉向架點頭頻率和車體一階彎曲頻率相近，也不會發生彈性車體與轉向架的共振。

4)隨著減振器阻尼系數的增大，車輛的運行平穩性迅速改善后又緩慢變差，在阻尼系數為6 000N/(m·s-1)時平穩性達到最優。車體平穩性隨著空氣彈簧剛度減小而變好，即空氣彈簧越“軟”，車輛運行的平穩性越好。