化歸思想在圓柱教學中的滲透

一、化歸思想的定義

人們在面對數學問題，當直接應用已有知識不能或不易解決時，一般會把需要解決的問題不斷轉化形式，歸結成能夠解決或比較容易解決的問題，最終使原問題得到解決，人們把這種思想方法稱為化歸思想。

南京師大的喻平教授認為，應用化歸思想時，要遵循四個基本原則：①數學化原則，就是把生活中的問題轉化為數學問題，建立數學模型，應用數學知識解決問題；②熟悉化原則，就是把陌生的問題轉化為熟悉的問題；③簡單化原則，就是把復雜的問題轉化為簡單的問題；④直觀化原則，就是把抽象的問題轉化為具體的問題。［2］

因此，在小學數學教學中，要將化歸的數學思想和方法滲透到各個環節。下面筆者以圓柱的教學為例，淺析如何在課堂教學中恰當地運用化歸思想，提高學習效率。

二、化歸思想在圓柱課堂教學的滲透

圓柱的教學是“新人教版”六年級數學下冊第三單元“圓柱與圓錐”第一小節內容。它分為三個層次：第一，結合實物探索圓柱的特征；第二，探索圓柱表面積的計算方法；第三，探索圓柱的體積計算公式的推導過程。

在圓柱的課堂教學實踐中，筆者主要從以下五個方面滲透和運用了化歸思想和方法。

1.把未知問題轉化成已知問題。如在學習圓柱的體積時，筆者就課本提出的問題入手：我們能不能把圓柱轉化成我們已經學過的立體圖形，計算出它的體積呢？接著通過教師演示教具，把圓柱的底面分成許多相等的扇形，把圓柱切開，照教材的圖拼起來就近似于一個長方體。然后，進一步運用課件進行展示，將圓柱的底面逐步分成8等份、16等份、32等份的扇形，讓學生觀察了解：底面分成的份數越多，拼成的形體越接近長方體。接下來引導學生把拼成的長方體與原來的圓柱體比較，發現轉化前后長方體的底面積與圓柱體的底面積相等，長方體的高與圓柱體的高相等。因為長方體的體積等于底面積乘以高，所以圓柱體的體積計算公式是底面積×高，從而最終推導出圓柱的體積計算公式V＝sh或V＝πr2h的兩種形式。就這樣通過切割和拼接，把未知的圓柱體轉化成已知的長方體，從而推導出圓柱的體積公式，這一教學過程向學生滲透了轉化思想。

2.把整體問題轉化成局部問題。很多數學問題，如果從整體去進行思考和分析會比較復雜。此時不妨引導學生利用化歸思想，從問題出發，把不必要的已知條件過濾掉，打破常規思路，直接找出原問題的答案。如課本練習四第13題（24頁）：

一根圓柱形木料的底面半徑是0.3m，長是2m，將它平均截成4段，這些木料的表面積比原來木料增加了多少平方米？

有學生提出先求截成4段后的木料的表面積，再求出原來木料的面積，然后算出兩者面積之差，就知道增加了多少平方米。這個解題思路計算起來顯然非常麻煩。有沒有更簡單的解題方法呢？

筆者提問： “在圖中，截成4段后木料比原來多出來的是哪個面？”學生通過觀察附圖發現：把圓柱形木料截成4段后，表面積比原來增加了3×2=6個底面。由此求出一個底面積再乘以6，即可解決問題。這種方法比用4段木料總面積減去原來木料的面積無疑更省事，實際上只需把整體的問題變成局部問題，抓住圓柱的切割特點，找出截成4段表面積增加的部分，問題就得以解決。

3.把隱蔽問題轉化成具體問題。課本練習五的13題（29頁）：小雨家有6個底面積是30cm2、高10cm的圓柱形水杯，沏一壺茶水能倒滿4杯，有一天來了6位客人，如果讓6位客人都能喝上這壺茶水，平均每杯倒多少毫升？

這道題的已知條件很多，但與問題之間的聯系比較隱蔽，要想解決這個問題，首先要對題中的條件進行化歸，將隱蔽的問題明朗化和具體化。題目的已知條件是茶杯的底面積和高，求平均每杯倒多少毫升茶，就是把一壺茶水平均分成6份，其實是求把4個茶杯的容量平均分成6份，每份是多少毫升。

根據以上條件和問題，筆者用化歸思想引導學生將問題進行分解：

（1）1個茶杯容量是多少毫升？（2）4茶杯是多少毫升？（3）6位客人平均分這4杯茶，每人分得多少毫升？

通過這樣分解，學生很快就理清了題目中的數量關系，求出答案。

由此可見，在解決較隱蔽的問題時，利用化歸思想可以將問題進行分解轉化，把問題變得簡單具體。

4.把生活問題轉化成數學問題。在圓柱教學中常常碰到生活中的實際問題。在解決這類問題時，筆者引導學生先將問題進行符號化，也就是數學化。然后再進一步考慮，選擇什么樣的數學知識解決問題。

練習課上有一道題：用塑料薄膜覆蓋的蔬菜大棚，長15米，橫截面是一個直徑2米的半圓（如圖）。

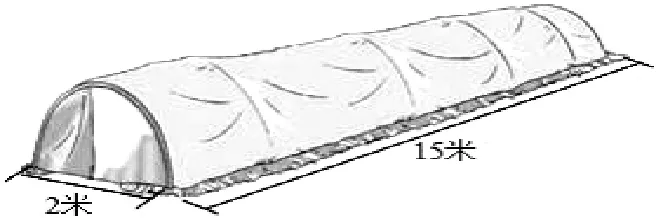
（1）這個大棚的種植面積是多少平方米？

（2）覆蓋在這個大棚上的塑料薄膜約有多少平方米？

（3）大棚內的空間約有多大？

要解決大棚的種植面積、塑料薄膜的面積和大棚內的空間這幾個實際問題，首先將這幾個實際問題進行數學化，將題目上已知條件實際數字和問題轉化成數學條件后，就變成了下面的數學問題：

（1）求長15米、寬2米的長方形的面積；

（2）求直徑2米、高15米的圓柱表面積的一半；

（3）求直徑2米、高15米的圓柱體積的一半。

通過把實際問題轉化為跟圓柱有關的數學問題后，就能輕松地用圓柱的知識去解決了。

5.把抽象問題轉化成簡單問題。有些數學問題的很多條件比較復雜，從而使問題看起來變得抽象。這時，我們可引導學生運用化歸的思想對題目中的抽象條件進行分析。

如例7（27頁），教材呈現了一個裝了小半瓶水的礦泉水瓶，下部是圓柱形，上部是一個不規則的立體圖形。給出了瓶子平置時水的高度和倒置時無水部分的高度，求這個瓶子的容積。

這是一個非常規的數學問題，簡單套用公式無法解決。首先，讓學生在理解題意的基礎上，明確這個瓶子不是一個完整的圓柱，無法直接用圓柱的體積公式計算它的容積。然后我們能不能把它轉化成圓柱呢？

接下來通過實物演示，引導學生觀察比較水瓶倒置前后的水瓶內的變化情況，發現無論是否倒置，水瓶的容積＝瓶內水的體積＋無水部分的體積。進一步觀察發現：水瓶倒置前后，水的體積與無水部分的體積都是不變的，并且倒置前，瓶內水的形狀是一個圓柱，而倒置后，無水部分的形狀也是一個圓柱，這兩個圓柱的體積之和就是瓶子的容積。通過實驗演示讓學生經歷了等積變形的轉化過程，把不規則形狀轉化為規則形狀，從而解決問題。

實踐證明，化歸思想的運用能使復雜的問題簡單化，抽象的問題具體化，從而抓住問題的本質，降低解決問題的難度。

綜上所述，化歸思想是學習者所應具備的數學思維，也是重要的數學解題方法。