一種基于標簽傳播的兩階段社區發現算法

鄭文萍 車晨浩 錢宇華 王 杰

1(山西大學大數據科學與產業研究院 太原 030006) 2(山西大學計算機與信息技術學院 太原 030006) 3(計算智能與中文信息處理教育部重點實驗室(山西大學) 太原 030006) (wpzheng@sxu.edu.cn)

復雜網絡分析在社會學、傳染病學和生物學等領域有著廣泛的應用[1-3].通常可以用圖G=(V,E)表示一個復雜網絡,其中V表示網絡中個體的集合,E表示個體間聯系的集合.社區結構(community structure)是復雜網絡的重要特征之一,即一個網絡可以分成若干社區,社區內節點之間連接相對緊密,社區間節點連接相對稀疏.有效的社區發現算法可以發現社會網絡中的社區結構、生物網絡中的蛋白質功能模塊等,有助于深入研究各種類型復雜網絡的功能模塊及其演化特征,對準確地理解并分析復雜系統的拓撲結構及動力學特性具有十分重要的理論意義和應用價值[4-5].

目前復雜網絡中的社區發現方法主要有基于圖劃分的聚類算法[6]、基于譜分析的聚類算法[7]、基于層次的聚類算法[8]和基于密度的聚類算法[9-10]等.Newman提出了一種基于貪心策略的快速社區發現算法(fast modularity maximization, FMM)[11],以最優化模塊性為目標函數進行社區合并和更新.Blondel等人提出了BGLL算法[12],隨機選擇一個節點作為初始社區,迭代選擇使當前社區模塊性增長最大節點加入當前社區完成社區擴展過程.由于現實網絡包含大量的小規模社區,網絡社區內部連接數不一定比社區之間的連接數多,導致模塊性不能較好地度量社區劃分質量.Bai等人[13]基于互補熵理論提出了一種度量網絡中社區發現質量的目標函數,該函數綜合考慮社區內緊密程度和社區間稀疏程度對社區發現結果進行評價,并以公共鄰居數度量節點相似性給出了一種圖聚類算法ISCD+.

Raghavan等人提出了標簽傳播算法(label pro-pagation algorithm, LPA)[14],該算法中起初每個節點擁有獨立的類標簽,每次迭代中對于每個節點將其標簽更改為其鄰居節點中出現次數最多的標簽,通過迭代,直到每個節點的標簽與其鄰居節點中出現次數最多的標簽相同,則達到穩定狀態,算法結束.此時具有相同標簽的節點屬于同一個社區.LPA算法有接近線性時間的復雜度,但劃分過程中,節點更新順序與標簽傳播過程存在很大的隨機性，使劃分結果表現了較強的不穩定性.Barber等人對LPA算法進行改進提出算法LPAm[15],參照隨機連接定義節點標簽更新方式,使得算法結果具有較高的模塊性.然而,LPAm算法可能陷入局部最優解且結果存在不穩定性.Liu等人提出LPAm+算法[16],在LPAm算法之后引入后處理步驟，合并一些小社區進一步提高劃分結果的模塊性.Li等人基于LPA算法提出一種分階段的社區發現算法LPA-S[17],依據節點間的相似性更新節點標簽,得到初始社區劃分；再根據社區相似性進行社區合并,使得最終劃分結果中社區內部連邊具有較高的密度.

以上算法主要針對LPA節點標簽更新過程的不確定性進行了改進，并對劃分結果進行適當處理以緩解過早陷入局部極值的問題.盡管如此，這些算法沒有處理節點標簽更新順序的隨機性，使得劃分結果仍然存在較大的不穩定性.按合理的順序選擇待更新節點可以提高算法性能并得到穩定的社區劃分結果.針對此問題，本文提出了一種基于標簽傳播的兩階段社區發現算法(a two-stage community detection algorithm based on label propagation, LPA-TS)，減少了傳統標簽傳播方法在節點更新和標簽傳播過程的隨機性,可以得到穩定的計算結果；通過與一些經典算法在8個真實網絡以及不同參數情況下LFR benchmark人工網絡數據集上的實驗比較分析，結果表明LPA-TS算法社區發現結果表現了良好的穩定性,且在標準互信息、調整蘭德系數、模塊性等方面均表現出較好的性能.

1 背景知識

一個復雜網絡可以用圖G=(V,E)來表示,其中節點集V={v1,v2,…,vn}表示網絡個體的集合,邊集E代表網絡個體間聯系的集合,記作邊ei,j=(vi,vj).令n=|V|且m=|E|.除非特別聲明,本文僅對無向簡單圖進行討論.在圖G中,節點vi的鄰域NG(vi)定義為NG(vi)={vj|(vi,vj)∈E},其中vj∈NG(vi)稱為節點vi的鄰居節點.節點vi的度為d(vi)=|NG(vi)|,在不引起混淆的情況下,簡記為di.假設Ω={V1,V2,…,Vk}是V的一種劃分,Vr∈V且|Vr|=nr,稱k為該劃分中的社區個數.令di(Vr)=|{vj|(vi,vj)∈E且vj∈Vr}|表示節點vi與社區Vr內節點的連邊數.

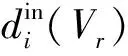
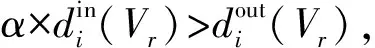
(1)

而弱社區是指社區中所有節點與社區內部節點的度數之和大于社區中所有節點與社區外部節點連接的度數之和:

(2)

默認取α=2.通常一個社區應該至少表現弱社區的性質.

2017年，Bertolero等人定義了節點的參與系數[19]，用來刻畫節點與網絡中不同社區連邊的分布情況:

(3)

參與系數的值越高則表示節點與較多社區存在連邊，該節點對某社區的歸屬度比較低；相反，值越低表示節點的連邊情況越集中于少數社區，則該節點對某社區的歸屬度較高.從具有明顯社區歸屬的節點開始進行社區發現，有助于提高社區發現質量，并提高算法穩定性.

為了對社區劃分結果進行度量，2004年Newman等提出了模塊性[20]的概念，它反映了網絡社區內部連接的強弱，作為一種社區劃分的評價標準得到了廣泛使用.將網絡用鄰接矩陣A來表示，若節點x與y直接相連，則Ax y=1，否則Ax y=0.模塊性定義為

(4)

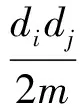
為了合理地對復雜網絡中的節點進行社區發現，將節點間相似性作為衡量節點連接緊密程度的重要標準.目前已經有一些基于網絡拓撲特征的相似性度量函數[21-22].公共鄰居數(common neighbors, CN)度量[21]認為2個節點間的公共鄰居節點越多，則它們在結構上越相似，連接越緊密:

CN(x,y)=|NGx∩NGy|.

(5)

2 一種基于標簽傳播的兩階段社區發現算法

基于節點參與系數與節點相似性，本文給出一種基于標簽傳播的兩階段社區發現算法(LPA-TS).算法包括2個主要過程：1)根據節點參與系數定義節點的更新順序，并更新節點標簽為與其具有最高相似性的鄰居節點標簽，得到社區的初始劃分結果；2)將當前社區進行合并，并在目標函數的監督下完成社區劃分的過程.第1階段中首先根據節點的參與系數高低，從低到高確定節點的更新順序；其次依據節點相似性，選擇與當前遍歷節點最相似的鄰居節點的標簽作為當前遍歷節點的標簽，得到第1階段的劃分結果.第2階段中，將社區作為節點計算其參與系數以確定社區合并順序，最后在目標函數的監督下將社區進行合并得到最終的劃分結果.

2.1 節點更新順序

在LPA算法中，不同的節點更新順序會使得最終的社區劃分結果有很大差異.如圖1所示，可以看出，圖1中7個節點應該被分成2個社區.算法初始將每個節點看作1個單獨社區，假設當前虛線框住的節點已經被賦予了相同的社區標簽.隨后，若首先選擇節點v4進行標簽更新，有很大可能將節點v4與節點{v1,v2,v3}劃分到同一社區，進而將所有節點劃分為1個社區.而如果選擇節點v5進行更新則會有很大可能得到正確的社區劃分.這是由于節點v4位于2個社區的邊界處，對社區的歸屬度不強，對其首先更新容易將2個社區合并為1個大社區.

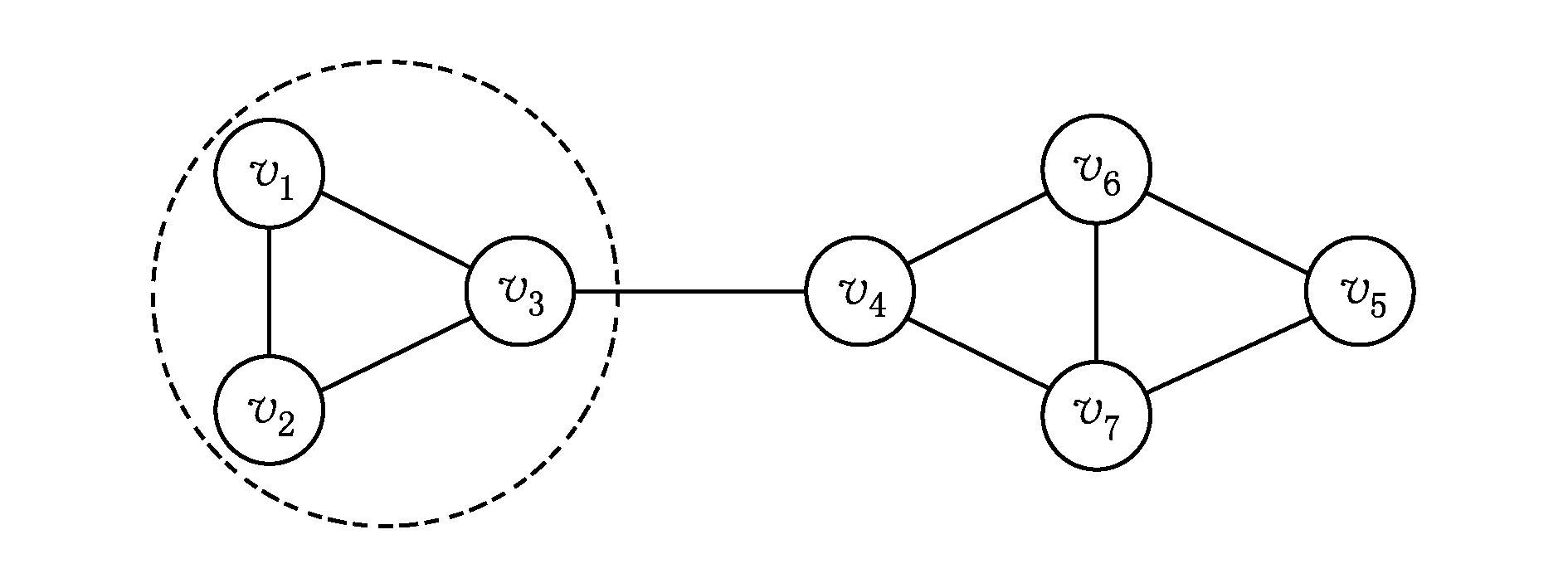
Fig.1 An example network with two communities圖1 具有2個社區的網絡示例

可以看出，在節點標簽更新的過程中，如果先更新歸屬度較強的社區內部節點的標簽，會獲得一個更符合實際社區結構且更穩定的劃分結果.

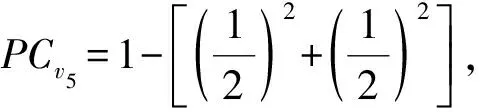
從參與系數的定義看，一個節點的度越低，其社區歸屬程度越高；而一個節點的鄰居節點社區歸屬越集中，其社區歸屬程度越高.優先選擇參與系數低的節點進行更新，可以盡早得到更穩定的社區結構，進而得到更準確的社區劃分結果.如圖1最終得到2個社區劃分{v1,v2,v3}和{v4,v5,v6,v7}.

2.2 標簽傳播

LPA算法在對節點的標簽進行更新時，選取鄰居節點的標簽中出現次數最多的標簽為自身標簽，即認為其所有鄰居節點的重要性相同，并沒有考慮不同鄰居節點的不同相似性.然而，在同一個社區中的個體往往具有較高的相似性.如在圖1中，節點v4、節點v6和節點v7具有相同PC值，對于節點v4，其鄰居節點的標簽出現次數均為1，則有較大可能將v4劃分入社區{v1,v2,v3}，導致錯誤的劃分結果.

實際上,對節點v4而言,社區{v1,v2,v3}，{v6}和{v7}中各有一個節點與其關聯，從圖1中可以看出，由于v4與v6(或v7)有一個公共鄰居節點，因此相較于節點v3，v4更有可能與v6(或v7)屬于同一社區.

因此，用CN對節點間的相似性進行度量，2個節點間的公共鄰居節點越多，則它們在結構上越相似，連接越緊密，在標簽更新的過程中選擇與其相似性最高的鄰居節點的標簽，可使最終劃分在同一個社區中的節點具有較高的相似性，也更符合實際的社區分布.如在圖1中，節點v4確定標簽時，由于其與節點v6和節點v7的相似性高于其他節點，故標簽會確定為節點v6或節點v7的標簽，得到正確的劃分.但是公共鄰居數度量節點相似性在某些特殊情況下并不適用.例如若節點x和節點y之間存在連邊,但無公共鄰居節點，但它們之間的相似性應該大于0；特別地，一個懸掛點與其相鄰點之間無公共鄰居節點，但通常與其相鄰點位于同一社區.基于此，本文對節點相似性計算為

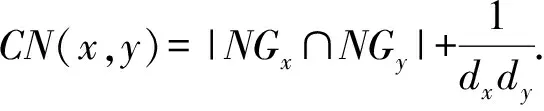
(6)

2.3 初始社區發現過程

根據節點更新順序和標簽傳播過程，算法給出網絡初始劃分結果.首先將網絡中的每個節點看作一個獨立社區，賦予唯一社區標簽；計算節點的參與系數PCi(1≤i≤n)，按從低到高的順序依次更新節點標簽.節點標簽更新過程中，考慮當前節點與其鄰居節點的公共鄰居相似性，選擇相似性最高的鄰居節點標簽作為當前節點的新標簽.以上過程迭代進行，直到劃分結果不再變化或者達到最大迭代次數.算法1給出LPA-TS算法的第1階段即初始社區發現過程.

算法1.初始社區發現算法(LPA-TS第1階段).

輸入：網絡G=(V,E)、最大迭代次數tmax，其中V={v1,v2,…,vn}，A是圖G的鄰接矩陣；

輸出：網絡的初始劃分結果L(V)={l1,l2,…,ln}，其中，li表示節點vi的初始劃分社區標簽.

步驟1.根據

計算網絡中節點vi和vj間的相似性.

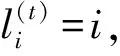
步驟3.計算當前節點標簽集合中不同的標簽數k=|L(V)|.

步驟4.根據

計算節點vi的參與系數.

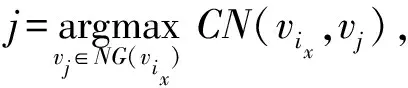
步驟7.t=t+1.

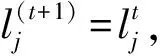
圖2給出了在Karate網絡上的初始社區發現結果.其中節點被初始劃分為4個社區(用不同形狀表示).可以看出，算法1的初始社區劃分結果中，度數較大節點由于與鄰居節點的相似性較高，容易將自身標簽傳播給鄰居節點，從而形成以大度節點為中心的較大社區.而位于社區邊緣的一些節點，由于度數偏低且與鄰居節點的相似性小，容易形成一些規模較小的社區，如圖2中菱形節點和三角形節點構成的社區.

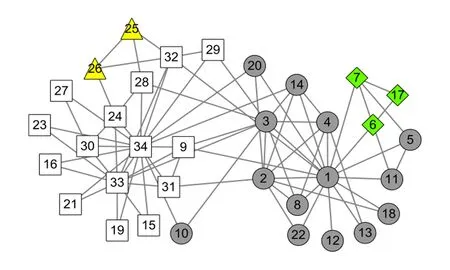
Fig.2 Communities of the Karate network discoveredby Step 1 of LPA-TS圖2 LPA-TS第1階段在Karate網絡的初始社區發現結果

隨著網絡規模的增大，特別是網絡連接比較稀疏時，算法第1階段會得到大量的特別小規模的社區，造成對原始網絡的過劃分.為了得到更準確的社區劃分結果，還需要對初始社區劃分結果進行社區合并.

2.4 社區合并過程

針對初始社區發現過程網絡過度劃分的問題，首先分析得到的初始社區劃分結果中，根據式(2)依次判斷各初始社區是否滿足弱社區的定義.通常情況下，式(2)中的內部度系數α=2，表示一個社區的內部度大于其外部連邊數則為弱社區.當所分析網絡中包含大量小規模社區時，特別是社區個數遠大于單個社區規模時，一個社區的內部度可能會小于其外部連邊.為更好地反映網絡的社區組成，此時，需要根據網絡類型適當提高式(2)中的內部度系數α.

將不滿足弱社區定義的初始社區，與其相鄰的且具有最多關聯邊數的社區合并為一個社區.在此為基礎上繼續進行LPA-TS算法第2階段的標簽傳播過程.

將以上所得的每個社區看作一個節點，社區之間連邊數作為2個社區對應節點連邊的權重，給出該帶權無向網絡中節點參與系數的定義方式：

(7)

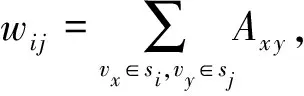
因此，此處仍然按社區對應節點的PC值從低到高的順序進行標簽更新.在節點si的標簽更新過程中，選擇與其具有最高連邊權重的鄰居節點標簽作為si的新標簽.每次節點標簽的更新都意味著合并2個初始社區.

為了對節點標簽傳播過程進行有效控制，需要從社區內部連接緊密程度以及社區間連接的稀疏程度同時考慮社區發現質量，因此本文選擇文獻[13]提出的基于互補熵的評價函數，對當前社區合并結果進行評價:

(8)

算法2給出了LPA-TS第2階段社區合并的具體過程.

算法2.社區合并過程(LPA-TS第2階段).

輸入：網絡G=(V,E)，其中V={v1,v2,…,vn}，網絡的初始劃分結果L(V)={l1,l2,…,ln}；

輸出：網絡的最終劃分結果Ω={V1,V2,…,Vk}.

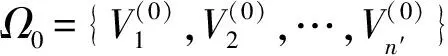
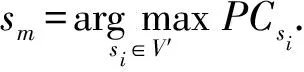
步驟5.計算當前網絡劃分的評價函數值F(Ωt+1).

步驟6.若F(Ωt+1)>F(Ωt)，令t=t+1，返回步驟2；否則，算法2結束，返回Ωt+1為最終結果.

2.5 時間復雜度分析

本文提出的基于標簽傳播的兩階段社區發現算法LPA-TS包括2個主要過程：

1) 根據參與系數定義節點的更新順序，并將節點標簽更新為與其具有最高相似性的鄰居節點標簽，得到社區的初始劃分結果；

2) 將初始劃分結果中的小規模社區與其有最多連邊的相鄰社區進行合并；本文采用基于互補熵的評價函數F(Ω)作為目標函數對社區發現結果進行判斷，得到F(Ω)值最大的社區發現結果作為算法最終輸出.

算法1中，計算節點相似性的代價為O(n2)，計算節點參與系數的代價為O(n2)；在算法2中，假設當前網絡中的社區數為n′，計算各社區間的連邊數的代價為O(n′2)；2階段的標簽更新的代價為O(t×(n+n′))，t為算法的迭代次數，因此算法LPA-TS的總時間復雜度為O(n2+n′2+t×(n+n′)).

3 實驗結果與分析

選擇不同參數情況下的LFR benchmark人工網絡[23]和8個經典真實網絡用本文算法LPA-TS進行社區發現，并選擇LPA,LPAm,LPAm+,LPA-S,BGLL,ISCD+,FMM,Infomap[24]等包括經典的標簽傳播算法和以模塊性為優化目標的算法作對比進行性能比較.

3.1 評價指標

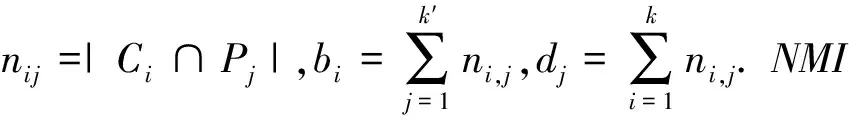
(9)

(10)

劃分結果與原始劃分的吻合程度越高，NMI和ARI的值越高.如果劃分結果與網絡隨機劃分結果相差越大，ARI的值更高.

為了對算法劃分結果的穩定性進行評價，本文定義算法的穩定系數σ.對網絡G，若|V(G)|=n，對第t次計算結果Ωt構造n×n階的矩陣，其元素定義為

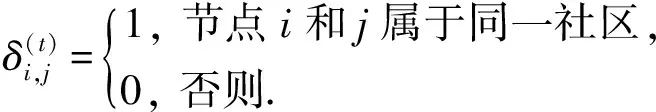
(11)

若算法運行T次，可得到計算結果的方差矩陣S，其元素定義為

(12)

由此，將算法穩定系數σ定義為

(13)

一個算法多次運行結果的算法穩定系數越低，說明算法劃分結果越穩定.

3.2 人工網絡實驗

人工網絡實驗采用在社區發現算法性能檢測中廣泛采用的LFR benchmark數據集上進行，分別考察網絡規模n為1 000或5 000，社區規模區間為10～50或20～100，混合參數μ為0.05～0.5的各種不同參數下LFR人工網絡上本文算法LPA-TS與對比算法的性能比較.所有實驗網絡節點平均度為20，最大度為50，節點度序列滿足指數為2的冪律分布，社區規模序列滿足指數為1的冪律分布.取各算法在每個網絡上執行30次的結果取平均值進行比較，結果如圖3和圖4所示.可以看到，混合參數較低(μ為0.05～0.3)時，網絡的社區結構比較明顯，各算法都取得了與實際網絡中社區分布高度吻合的結果.隨著μ的增大，網絡中社區結構明顯性降低，由于在本文LPA-TS算法中，選擇參與系數較低的節點進行標簽傳播，確保算法在保持社區發現質量的同時，減少了節點標簽傳播過程中的隨機性，從而使得算法運行結果比較穩定.

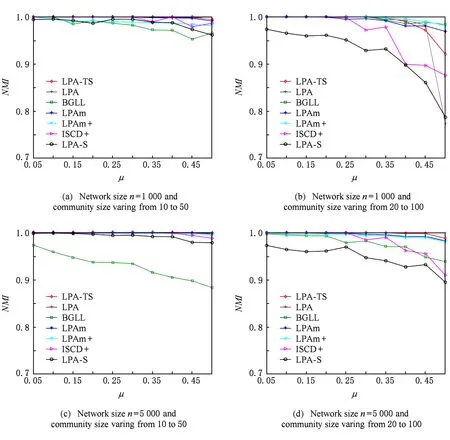
Fig.3 Comparison of NMI on LFR benchmark networks圖3 各算法在LFR benchmark網絡上的NMI比較結果

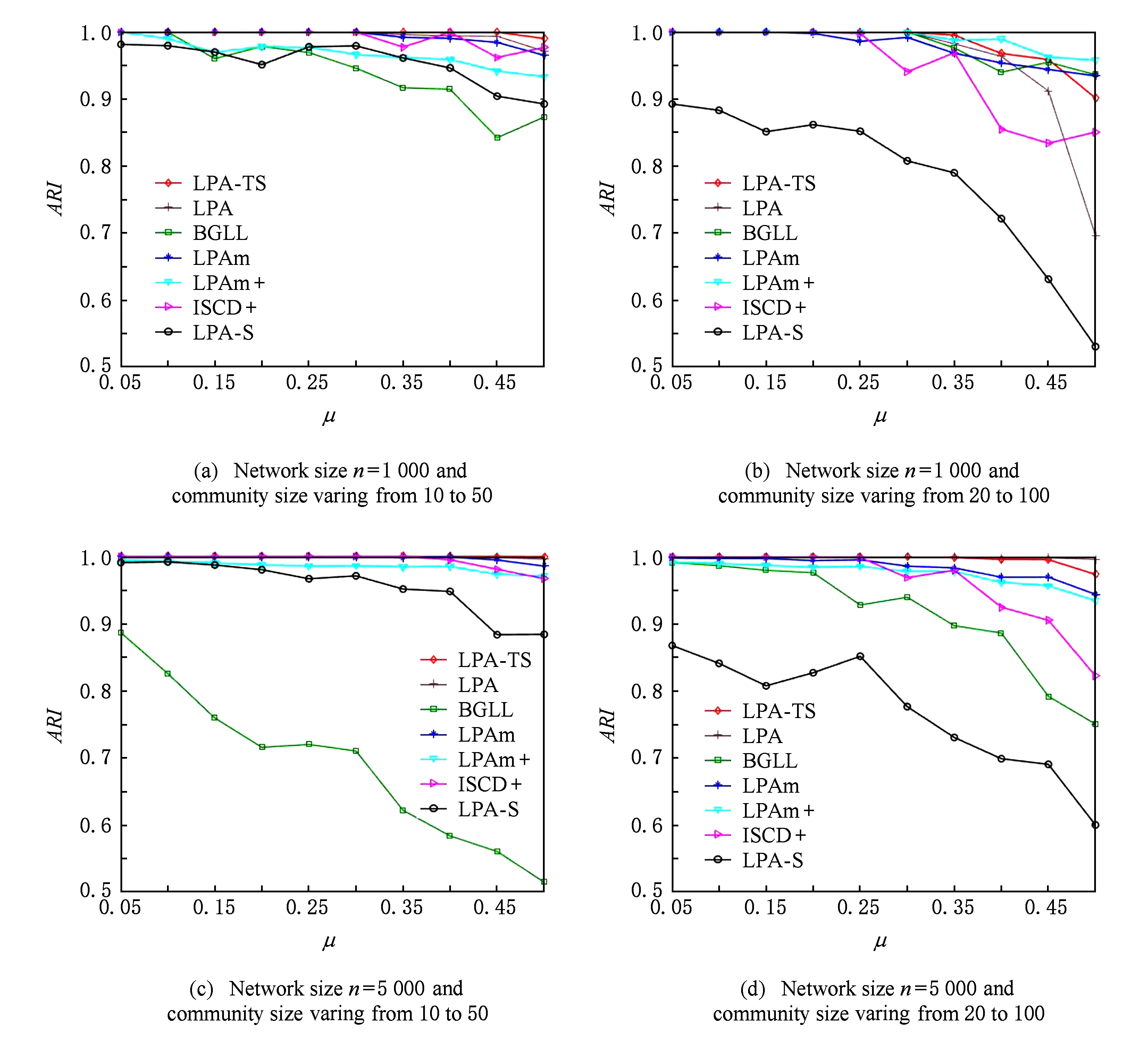
Fig.4 Comparison of ARI on LFR benchmark networks圖4 各算法在LFR benchmark網絡上的ARI比較結果

實際上，本文也與基于隨機游走的社區發現算法Infomap進行了對比實驗.Infomap算法在本文實驗的LFR benchmark網絡上社區發現結果與初始生成的社區劃分結果完全吻合.這是由于LFR benchmark網絡生成過程中，其社區內部連邊和社區之間連邊分別采用隨機連接方式產生.這導致網絡中各社區內部連邊分布比較均勻，2節點之間的連邊概率與其度數成正相關關系.所以LFR bench-mark網絡中社區分布比較平衡，網絡結構也相對穩定.因此，在LFR benchmark網絡上，本文所提算法LPA-TS和算法LPA-S在各類算法比較中的優勢沒有在真實網絡的實驗結果表現明顯.

然而，真實網絡的社區構成更加多樣化，社區內部連接和社區間連接也體現了很大的非平衡性.因此，我們進一步在經典的真實網絡上對各算法性能進行了比較.

3.3 真實網絡比較實驗

在本節中,我們通過在空手道俱樂部(Zachary’s Karate Club)[27]、海豚社交網絡(Dolphins Social Network)[28]、Polbooks[13]和大學生足球網絡(American College Football Network)[29]四個帶標簽的真實網絡以及Les Misérables[30]，NetScience[31]，Email[32]和Yeast[33]四個無標簽的真實網絡上進行實驗以對算法進行評測.數據基本情況如表1所示:

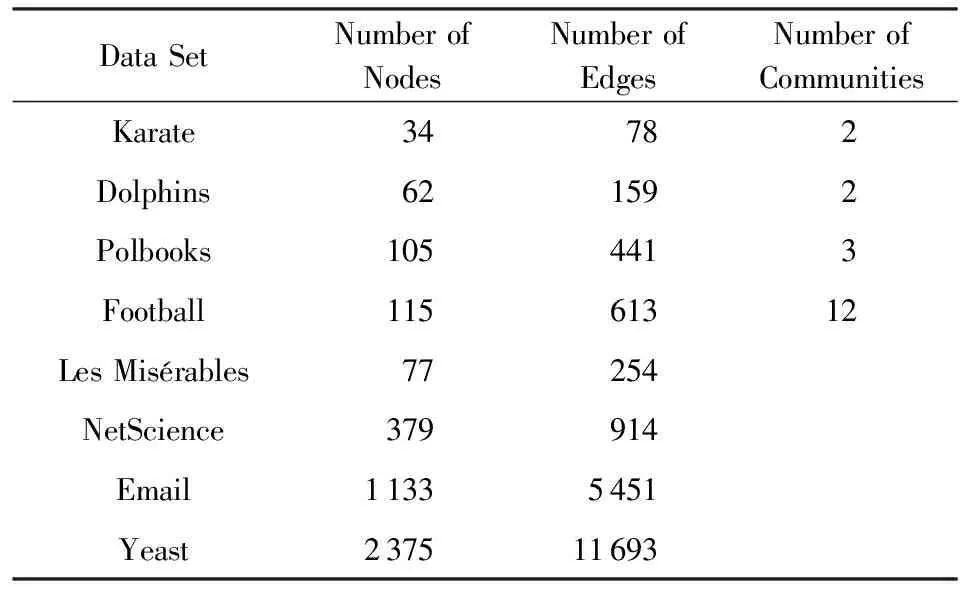
Table 1 Real Network Datasets表1 真實網絡數據集

由于LPA-TS算法引入了弱社區判斷，以適應復雜的真實網絡中多樣性的社區變化，使其在真實網絡上表現良好.算法比較結果如表2和表3所示，其中每個算法運行30次，取各項指標的平均值做比較.評價指標k表示算法最終發現的社區個數，Q是模塊性指標，time表示算法運行時間，σ是算法穩定系數.

表2給出了算法LPA-TS與8種經典社區發現算法FMM,LPA,BGLL,LPAm,LPAm+,Infomap,ISCD+,LPA-S在有標簽網絡數據集的實驗比較結果.可以看出，當網絡規模較小時，各算法所發現的社區個數與實際社區數吻合得較好，算法穩定性也表現良好；隨著網絡規模的逐漸增大，本文算法LPA-TS在社區個數和結果穩定性方面表現突出.

圖5給出了經典LPA算法在Karate網絡上的3種不同的劃分結果，由于其在節點更新順序上的隨機性，LPA對于網絡的劃分結果存在較大的不穩定性，甚至在劃分過程中會將整個網絡中的節點劃分在一個社區中.

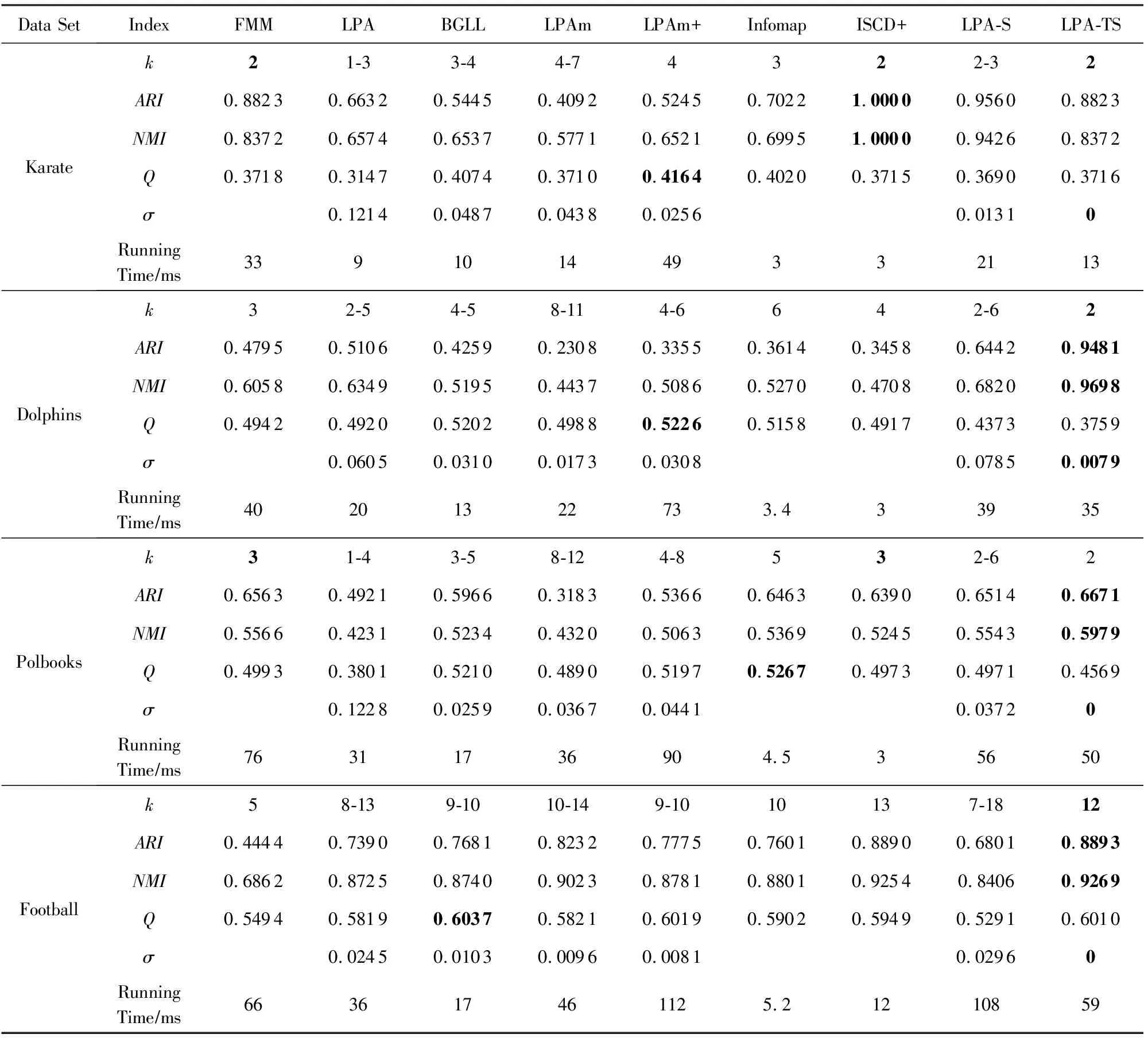
Table 2 Comparison of Real Networks with Labels表2 帶標簽真實網絡實驗結果對比表

Notes: Bolded part indicates the best result among the 9 algorithms.

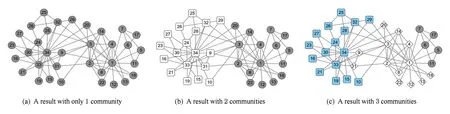
Fig.5 Different results of the LPA on Karate network圖5 LPA算法在Karate網絡上的3種不同的劃分結果

圖6給出了本文算法LPA-TS在Karate網絡上的劃分結果，將該網絡穩定地劃分為2個社區.

圖7給出了本文算法LPA-TS在Dolphins網絡上的一種劃分結果，該網絡表示62只寬吻海豚之間相互聯系的情況，節點表示海豚，若2只海豚間存在頻繁聯系則對應節點間存在邊，Dolphins網絡中有2個社區標簽.LPA-TS可以得到2種不同的劃分結果，這2種劃分結果的區別僅在于節點40(圖7中虛線圈出的節點)的社區歸屬.

Fig.6 Result of LPA-TS on Karate network圖6 LPA-TS在Karate網絡上的劃分結果

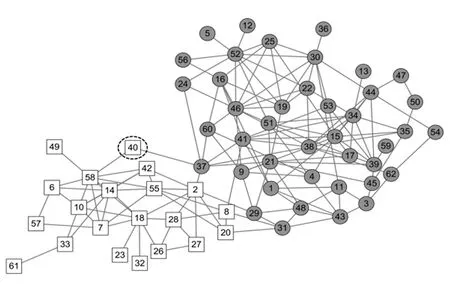
Fig.7 Result of LPA-TS on Dolphins network圖7 LPA-TS在Dolphins網絡上的劃分結果

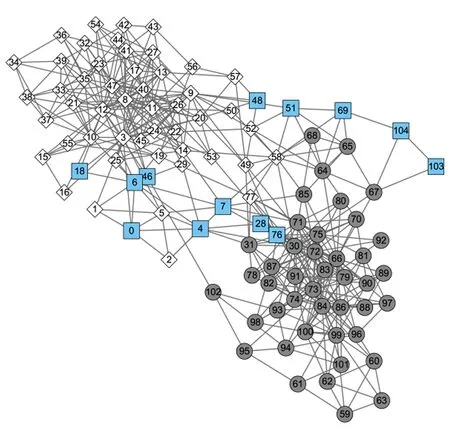
Fig.8 Primitive division on Polbooks network圖8 Polbooks網絡原始劃分

圖8給出了Polbooks網絡的原始劃分情況.該網絡節點表示在Amazon在線書店上銷售的與美國政治相關的圖書，如2本圖書曾被同一用戶購買過，則對應節點之間存在一條無向邊.這些圖書被分為3類：“自由派”(圓形節點)、“保守派”(菱形節點)和“中間派”(方形節點).可以看到，“自由派”和“保守派”這2個社區內部連接比較緊密，社區間連邊比較稀疏.而“中間派”節點代表的圖書沒有明顯的政治傾向，其對應的社區結構也并不明顯，這給社區發現算法的結果準確性和穩定性帶來一定的困難.從表2可以看出，本文算法LPA-TS在NMI,ARI等指標上表現更好；與LPA,BGLL,LPAm,LPAm+,LPA-S 五種結果呈現隨機性的算法相比，LPA-TS的算法穩定系數更低，因此運行結果比較穩定.圖9給出了本文算法LPA-TS在Polbooks網絡上所得的最終劃分結果，將Polbooks網絡劃分為2個社區，且各社區內部的連邊都比較稠密，社區間的連接比較稀疏，本文算法得到較為合理的劃分.

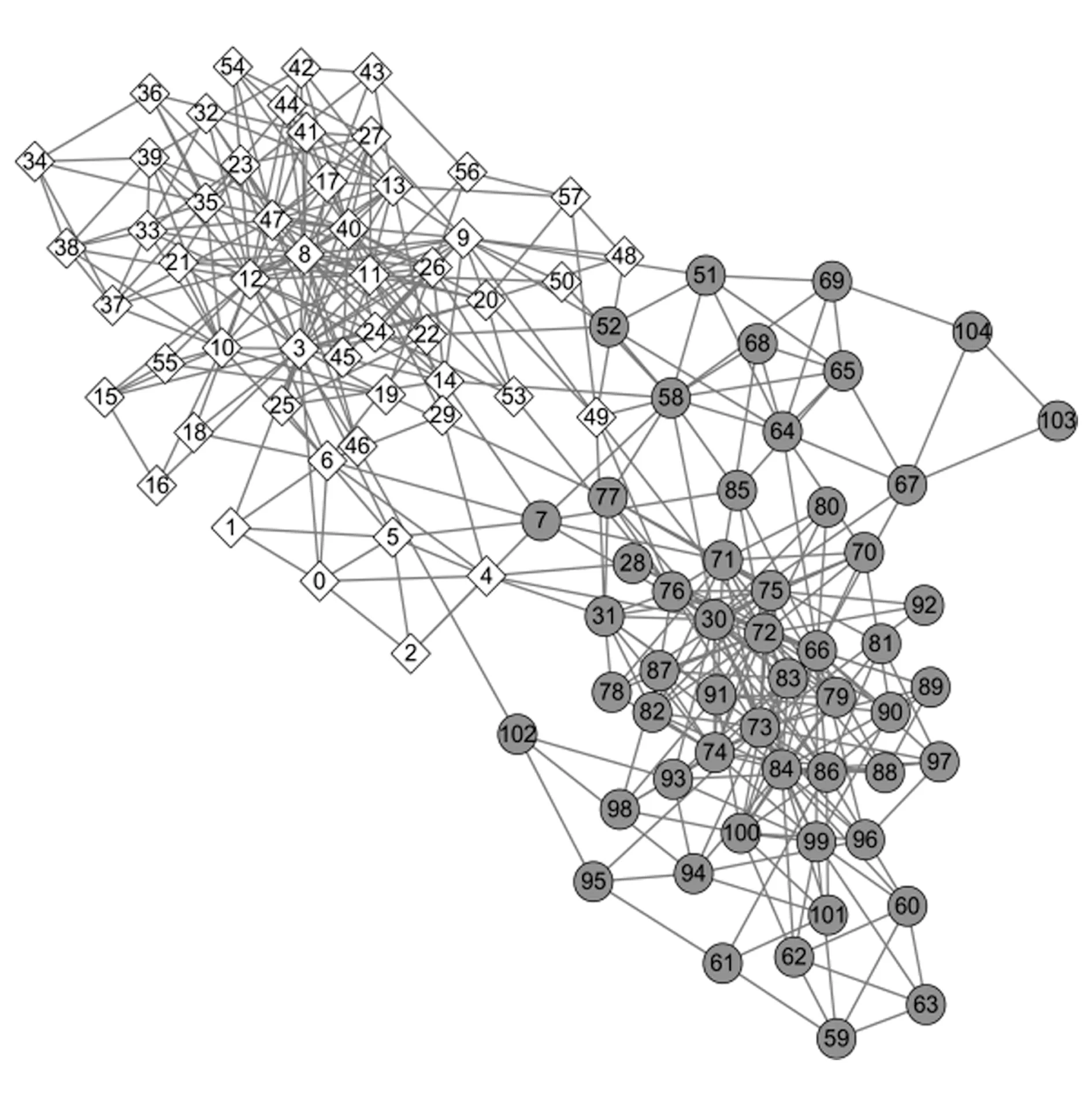
Fig.9 Result of LPA-TS on Polbooks network圖9 LPA-TS在Polbooks網絡上的劃分結果

Football網絡是根據美國大學足球聯賽2000年一個賽季的比賽賽程而建立的實際網絡，共有12個足球聯盟，每個球隊都屬于某一個聯盟，因此包含12個社區標簽.若2支隊伍之間進行過比賽，則對應節點間存在連邊.圖10給出了LPA-TS在Football網絡上的劃分結果，與真實劃分更為接近.

可以看出,在帶標簽的真實網絡數據中,社區劃分的模塊性并不一定很高，這是因為真實網絡社區結構更加多樣化，模塊性不能完全反映這種情況.

表3給出了算法LPA-TS與其他8種經典社區發現算法在4種無標簽真實網絡上的實驗結果，分別從劃分結果的模塊性和穩定性2個方面對各算法性能進行比較.可以看出，本文算法LPA-TS的穩定系數較低，說明其具有良好的穩定性.

Fig.10 Result of LPA-TS on Football network圖10 LPA-TS在Football網絡上的劃分結果

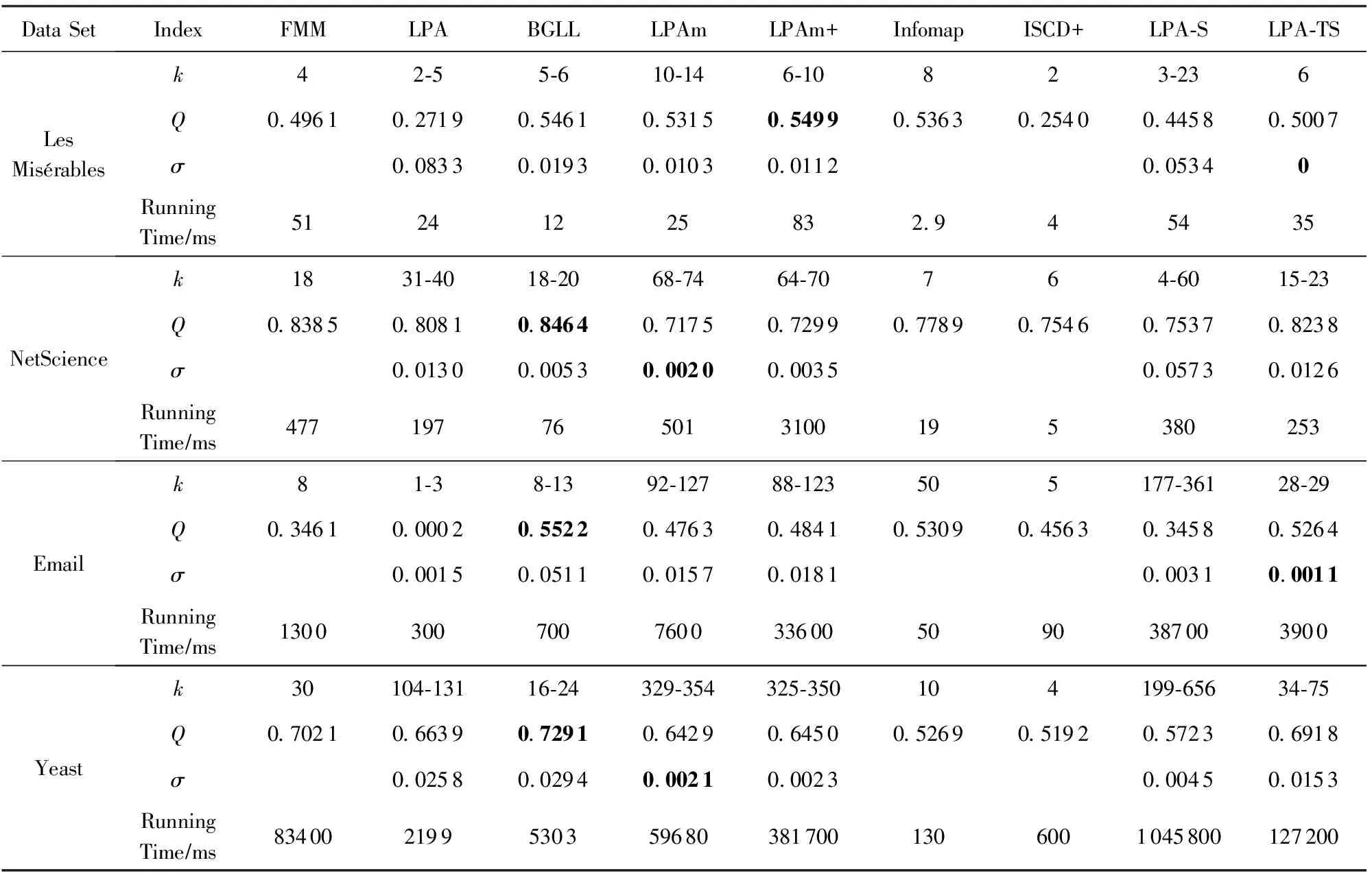
Table 3 Comparison of Real Networks without Labels表3 無標簽真實網絡實驗結果對比表

Notes: Bolded part indicates the best result among the 9 algorithms.

4 總 結

本文提出了一種基于標簽傳播的兩階段社區發現算法，通過節點的參與系數確定節點更新順序，并在標簽傳播過程中依據節點間相似性更新節點標簽，得到社區的初始劃分結果.判斷得到的初始社區是否滿足弱社區定義，若不滿足則將其與相鄰連邊最多的社區進行合并.將初始劃分得到的社區看作節點，社區之間的連邊數作為節點間的邊權重，得到社區關系網絡，并按照參與系數由低到高的順序合并社區關系網絡中的節點，得到最終的社區劃分結果.

通過與FMM，LPA，BGLL，LPAm，LPAm+，ISCD+，LPA-S等經典社區發現算法在不同參數情況下LFR benchmark人工網絡數據集以及真實網絡上的實驗比較分析，結果表明:由于LPA-TS算法減少了在節點更新和標簽傳播過程的隨機性，社區發現結果表現了良好的穩定性，且在標準互信息、調整蘭德系數、模塊性等方面均表現出較好的性能.

實際上，現實復雜網絡中存在復雜多樣的社區分布情況，如存在大量的小規模社區、社區規模分布呈現非平衡性、小社區內部連接數比社區間連接數少、網絡結構的動態性等特點，這給復雜網絡社區發現問題帶來了多方面的挑戰，未來將針對復雜網絡中這些特殊的社區結構特點，研制有效的社區發現算法.