基于遺傳算法的農業機械優化設計

鄭 濤，朱建錫，費 焱，陳長卿，徐文碩

（浙江省農業機械研究院，浙江 金華 321017）

農業機械設計是機械設計中的一個分支部分，農業機械優化設計是一門新興學科，優化設計能為機械設計及其制造提供一種優化途徑，必然也能在農業機械設計方面發揮優化設計的特點，使得在遇到相對復雜的條件時，能科學地挑選出一種最適合的設計方案［1］。經過多方實踐驗證，優化設計方法運用在農業機械設計及制造方面，可改變農業機械一貫以來簡單、粗糙、笨重等設計特點。不僅使得農業裝備更加輕便，還能減少制造成本，最主要還能提高農業裝備的精度、性能和質量。

優化設計有很多種算法，其中最常用的優化算法可按搜索方法不同分為兩大類：強搜索方法和弱搜索方法。如梯度法和牛頓法都屬于強搜索方法，其特點是利用目標函數及約束函數的梯度信息以確定性方式進行搜索。其優點是收斂速度較快，自然就能提高搜索效率，其缺點也比較明顯，即常常得出局部最優解，并非全局最優解。如隨機法和窮舉法都屬于弱搜索方法，其特點是通過在指定空間內大量地隨機采樣搜索。其優點是能夠完成非凸和不連續的目標函數的搜索，得出的結論往往有很大的概率即是全局最優解。自然缺點也是顯而易見，即收斂速度慢，導致搜索范圍越大搜索效率越低。強搜索和弱搜索這兩大類方法在實際應用范圍上各有局限性，但其各自的優缺點互補，因此若有一種新的算法能結合兩類搜索方法的優點，既能滿足不局限于局部最優解，又能在較小區域內自適應地搜索到全局最優解［2］，這種介于強搜索方法和弱搜索方法之間的新算法即遺傳算法。

1 農機用彈簧的優化設計

遺傳算法因其具備強搜索方法和弱搜索方法各自的優點，故遺傳算法在機械設計中的應用非常廣泛，近些年在農業機械優化設計方面也凸顯了其優點，本文就采用農機用彈簧為實例來介紹遺傳算法如何應用在農業機械優化設計中。

彈簧的優化設計有其特點，即將結構參數設定為設計變量，性能參數設定為約束條件。優化的目標是：成本最低、質量最小、體積最小、使用壽命最長等。彈簧的性能參數即約束條件有：承載能力、變形量、剛度、自振頻率等；結構參數即設計變量有：彈簧直徑、中徑、工作圈數等。因此彈簧的優化設計是一個多種參數和多種約束同時存在的優化問題，采用普通的強搜索和弱搜索方法得出的結論大概率是局部最優解或者需要相當大的搜索范圍和非常長的搜索時間，并不適合解決這種優化問題。而基于遺傳算法的多參數、多約束的優化方法可以較簡便地對彈簧進行優化設計。

1.1 遺傳算法在農機用彈簧優化設計中的應用

舉例：有一彈簧，已知安裝高度H1=50.8 mm，安裝載荷F1=27.2 kgf，最大工作載荷F2=68 kgf，工作行程h=10.16 mm，彈簧工作頻率fr=50 Hz；彈簧絲用油回火的50CrVA鋼絲，進行噴丸處理；工作溫度為126℃；要求彈簧中徑為20 mm≤D2≤50 mm，彈簧總圈數為 4≤n1≤50，支承圈數n2=1.75；旋繞比c＞6；安全系數1.2；設計一個具有質量最輕的彈簧結構方案［3］。

（1）目標函數

式中：ρ為鋼絲材料的比重，ρ=7.8×10-6kg/mm3。

從而得：W=0.1925×10-4d2D2n1

（2）約束條件

疲勞強度的約束，由疲勞安全系數計算公式得：

式中取Smin=1.2

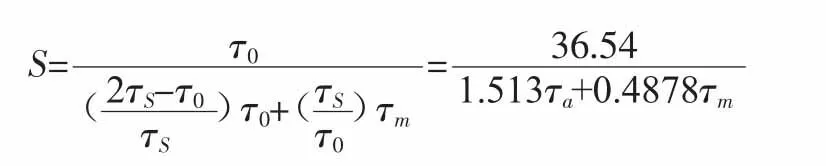
平均應力幅

根據旋繞比的要求的約束：

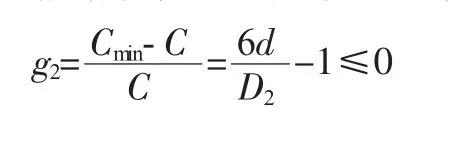
彈簧約束尺寸：4 mm＜d≤8 mm，20 mm≤D2≤50 mm，4≤n1≤50；

根據彈簧的穩定性條件：

式中：FC為壓縮彈簧穩定性臨界載荷。

彈簧自由高度：H0=（n1-0.5）d+1.2λ＝（n1-0.5）d+20.304

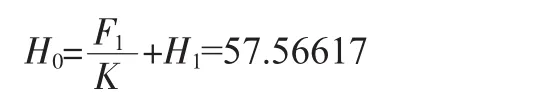
按一端固定一端鉸支考慮。

當高徑比 H0/D2≤3.7時，取 Fc=2F2=136 kgf，否則：

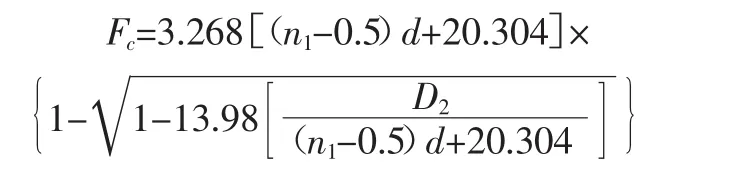
為了保證彈簧在最大載荷作用下不發生并圈：

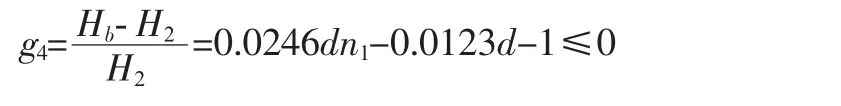
式中：H2=H1-h=50.8-10.16=40.64 mm

壓并高度 Hb=（n1-0.5）d

為了保證彈簧具有足夠的高度，要求彈簧高度與設計要求相符：Ka=K

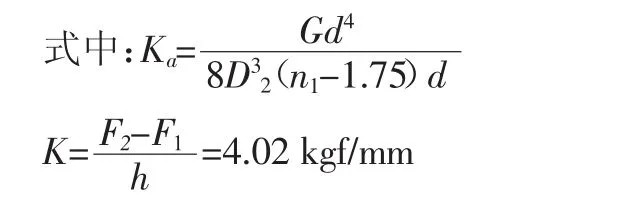
分析可知，以重量為目標的彈簧的設計問題是一個三維八約束的非線性規則問題，其中約束含6個不等式約束和2個等式約束。

（3）解決方法

①消元法可以解決等式約束。

由彈簧的安裝高度知：

由彈簧的剛度約束得：

②不等式約束的解決方法

彈簧的結構參數（設計變量），即對彈簧鋼絲直徑d的約束，可以以編碼的形式處理。其他的不等式約束可以作為確定遺傳操作可靠范圍的條件，主要目的是使個體只能存在于可靠范圍內。

（4）遺傳操作

①選擇：采用輪盤法與保留最優個體法，將前面所產生的一個最優的個體保留到當代。種群中個體的選擇概率為：

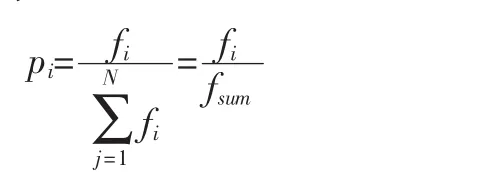
式中：fi為個體 i的適應度：fi=Wi-Wmin；Wi為個體的重量；Wmin為個體的最小重量；fsum為種群的總適應度；pi為個體i的選擇概率。

②交叉：交叉概率為1，每個變量都進行交叉，并且只能在可靠范圍內交叉。

③變異：變異概率為2%，并且只有在可靠范圍內的變異才生效。

④終止條件：連續五代種群的平均適應度不超過某一閥值。

（5）遺傳算法的優化結果［3］

根據遺傳操作的步驟，對本文所舉的農機用彈簧的優化設計問題通過MATLAB編程后自動優化計算10次。結果見表1。

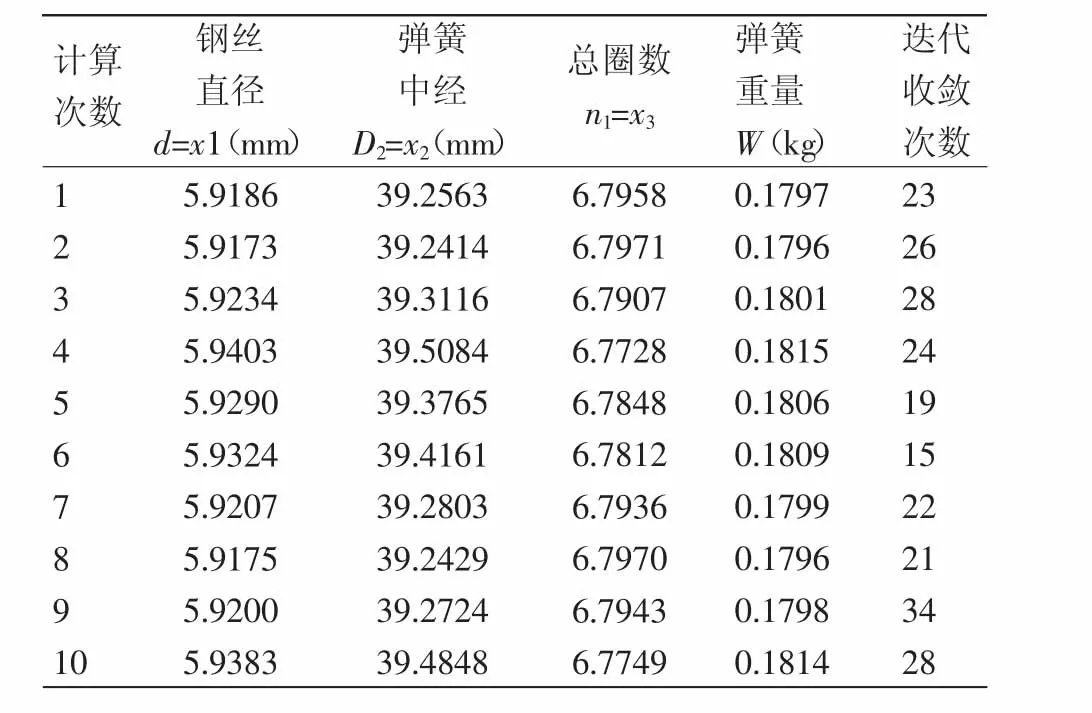
表1 彈簧優化結果

從表1可看出，迭代收斂次數各不相同，但10次優化的結果都非常相近。在滿足6個不等式約束和2個等式約束的要求下，從表中可得出彈簧鋼直徑為5.9173mm、中徑為39.2414mm、總圈數為6.7971時的重量最小，即為0.1796kg。

1.2 與傳統優化設計方法相比較

以濮良貴機械優化設計書中彈簧的優化設計為例。試設計一壓縮圓柱螺旋彈簧，要求其質量最小。彈簧材料為65 Mn。彈簧的最大工作載荷Pmax=40 N，最小載荷為0。載荷變化頻率為fr=25 Hz。彈簧的壽命為104 h，彈簧簧絲直徑1 mm≤d≤4 mm，中徑10mm≤D≤30 mm，工作圈數n≥5，彈簧旋繞比n≥4，工作溫度50℃，彈簧變形量≥10 mm。直徑d、工作圈數n、中經D為設計變量，優化目標為彈簧質量最小［4］。

文獻中采用常規優化方法求解，本文用遺傳算法來解決，即取搜索范圍為70，交叉概率為68.9%，變異概率為0.6%，遺傳總代數為20代，染色體長度為9（即每個設計變量以3位十進制位串表示），通過MATLAB編程計算，其結果對比如表 2 所示［5］。

表2 優化結果

通過表2中數據對比，遺傳算法得到的結果要明顯優于常規優化算法。此案例用遺傳算法進行優化設計時，經過5代遺傳便得到了優化結果，共計進行了117交叉，15次變異操作，表明遺傳算法具有很強的全局尋優能力，并能得到較好的解［5］。

2 遺傳算法在優化設計中的應用總結

（1）遺傳算法是比較新穎且相當有效的優化方法，特別適合解決多條件多變量的非線性復雜問題。而傳統的優化方法適合解決參數少的簡單問題。

（2）因遺傳算法和傳統優化算法有各自領域的優點，在遇到大型復雜問題時，并非采用單一方法，可以將遺傳算法和傳統優化算法相融合，發揮算法各自的優點，提高遺傳算法的搜索效率，降低迭代收斂次數，使其解決優化問題的范圍更廣。

（3）遺傳算法的可選參數較多，同樣的問題選取的參數不同，所產生運算結果也會有較大差異。為避免結果因此產生誤差，常根據經驗選取參數值后，多次獨立執行算法，結果將更接近全局最優解。如何選取這些控制參數以及如何使參數在遺傳算法中自適應調節，需進一步研究和探討。