一種三自由度并聯平臺運動學研究

， ，

(中國科學院長春光學精密機械與物理研究所航測二部，吉林長春130000)

0 引言

為適應非六自由度的機構設計，同時希望機構能具有并聯機構的運動響應快、結構剛度高、誤差小等優點，目前研究熱點逐漸移動到少自由度并聯機構[1]。少自由度并聯機構的本質是在六自由度的基礎上，在機構中加入了不同形式的約束[2]。通過不同的約束的布置形式將機構的自由度約束至合適的范圍。由于機構的約束形式各異，使機構表現為不同的特性。少自由度并聯機構具有驅動件少、結構簡單、控制容易的特點[3]。

在針對國內外穩定平臺和并聯平臺結構分析的基礎上[4-6]，借鑒現有的穩定平臺結構、驅動方式和控制方式等，結合穩定平臺所要求的結構簡單、成本低、承載能力大以及可移動性好等特點，設計出了三自由度并聯穩定平臺，其結構示意圖如圖1。

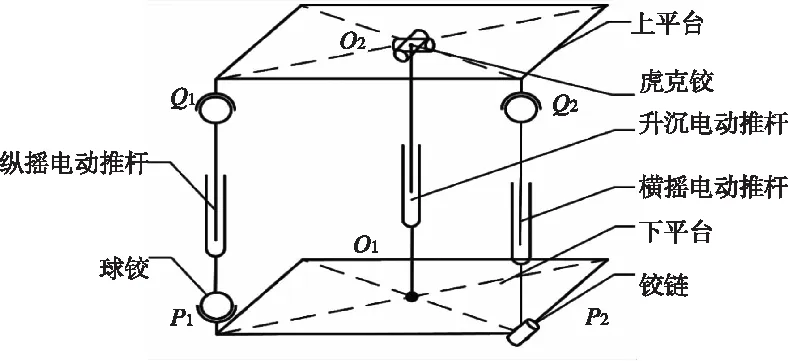
圖1 機構總體方案

此機構特點為升沉電動推桿上平臺和下平臺的中心，兩個轉動電動推桿分別等距分布在兩個轉動自由度方向上。上下平臺支點在平衡位置等距離(100 mm)布置(推桿與立柱平行)。平臺的轉角運動極限范圍是±20°，升沉運動的極限范圍是45 mm。兩個電動推桿關節結構分別為：UPS(雙端為球鉸，中間移動副)和RPS(一端球鉸，一端虎克鉸，中間移動副)。

1 運動學分析

1.1 正運動學分析

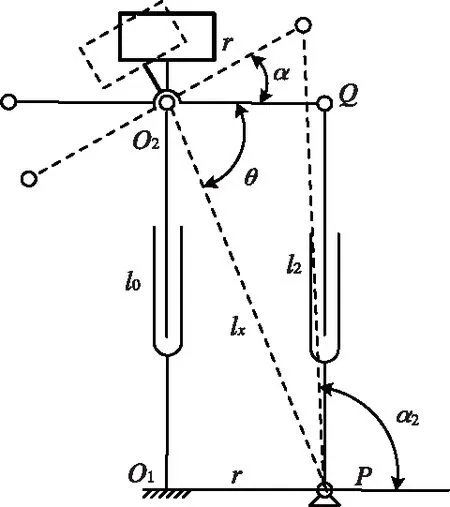
圖2 單軸旋轉運動簡圖

本文首先對縱搖四桿機構進行單獨的分析，對于一端球鉸一端鉸鏈的橫搖方向，應為鉸鏈的約束，其四桿在同一平面內，機構簡圖可以簡化為圖2所示。

其中坐標系O1-x1y1z1為基準坐標系。在機構中，r=100 mm為平臺中心到電動推桿立柱的距離，為O1P1、O1P2、O2Q1、O2Q2的距離，l0、l1、l2分別為升沉電動推桿、橫搖電動推桿和縱搖電動推桿的的長度，其取值范圍360 mm～520 mm。

圖中α為平臺轉動的角度，根據閉環矢量法建立方程：

(1)

根據公式(1)可得到：

(2)

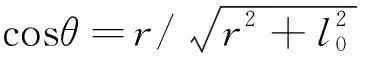
利用正余弦公式可計算出：

(3)

機構設計中：r為電動推桿和平臺連接處距平臺中點的距離為100 mm；l0和l2為升沉電動推桿的長度，其取值范圍為360 mm～520 mm；角θ為∠P2O2Q2，其值隨升沉電動推桿桿長的伸長量而改變，其值的運動范圍為1.30 rad～1.38 rad。將值帶入公式(3)可得：

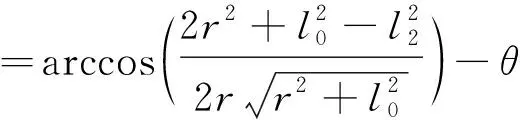
(4)

在雙軸進行轉動時，機構簡圖如圖3。

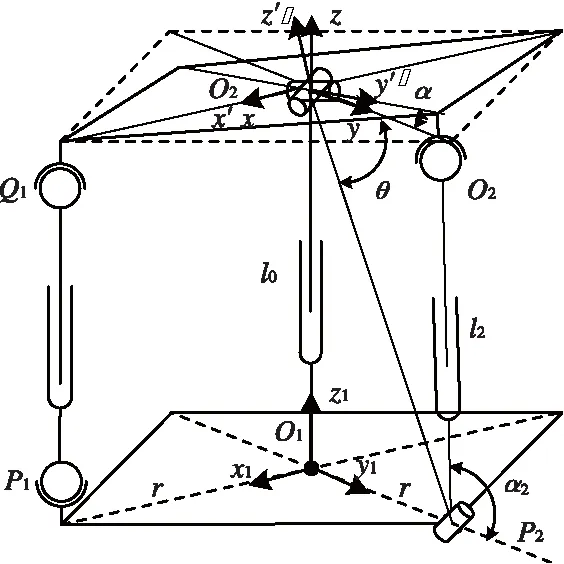
圖3 單軸旋轉運動簡圖

角α只受電動推桿l0、l1、l2的長度影響，角度值已由公式(4)得到。角β即受電動推桿l1的影響，又因為電動推桿l2會導致面O2Q1P1轉動。受到l0、l1、l2綜合影響。根據閉環矢量法列出公式：

(5)

因為在此轉動方向上O2Q1P1和O2O1P1不在同一平面，適用y軸上的方程需要根據兩個平面的分割線O2P2分為兩個方向。新列出閉環矢量方程：

(6)

根據結構模型，已知點O2處為虎克鉸，虎克鉸的兩個轉動副相互垂直。當電動推桿l2推動角α在某一定值時，O2Q1始終在垂直于O2Q2方向進行旋轉，同時面O2Q1P1垂直于O2Q2，β′為在面O2Q1P1中平臺轉動的角度，根據余弦定理可得：

(7)

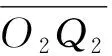
β=arccot(cotβ′·cosα)

(8)

1.2 逆運動學

因為空間機構計算較為復雜，逆運動學采用D-H法計算。D-H法研究機構各連桿之間的位移關系，通過計算相鄰連桿坐標系之間的轉換關系得到轉換矩陣，使用轉換矩陣表示其關系。通過坐標系的等價齊次變換矩陣，建立機構的運動方程。穩定平臺機構見圖2。在坐標系1和坐標2中，各點的坐標為：

1P1=(r，0，0)T2Q1=(r，0，0)T

1P2=(0，r，0)T2Q2=(0，r，0)T

(9)

1O1=(0，0，0)T2Q2=(0，0，0)T

將O1-xyz設為1坐標系(基準坐標系)，將O2’-x’y’z’進行平移，繞基準坐標系y軸旋轉β角，x軸旋轉α角，可得坐標系2。坐標轉換公式為：

(10)

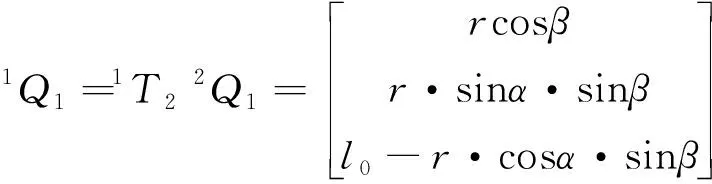
(11)

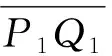
(12)

電動推桿長度l1為：

(13)

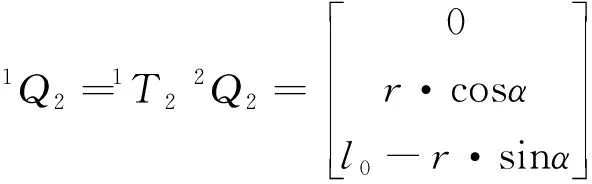
(14)

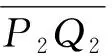
(15)

電動推桿長度l2為：

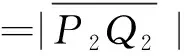
(16)

2 運動規律計算

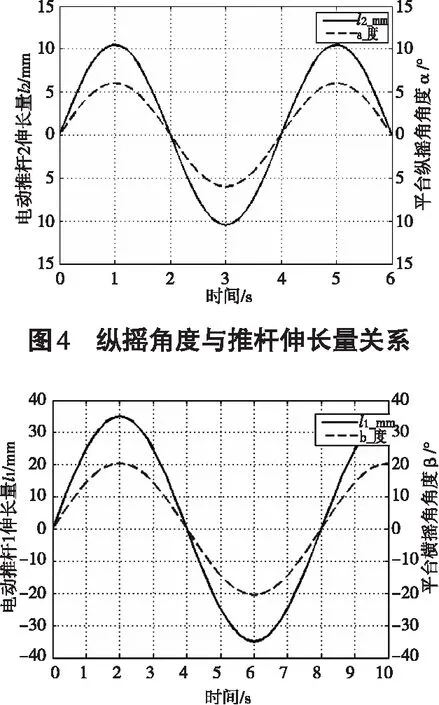
圖5 橫搖角度與推桿伸長量關系

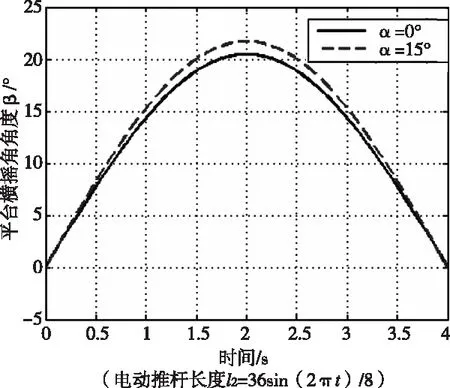
圖6 α不同時，耦合造成的平臺角度差別(電動推桿以相同規律運行)

根據本課題推導出的運動學模型，將所求得的公式帶入運動學的Simulink仿真程序。在實際系統中，平臺工作在橫滾角度為6°，縱搖角度為15°，升沉為40 mm的正弦運動中，根據計算出的公式對實際工作條件下并聯平臺進行仿真計算。其中a為角度α，b為角度β，l1為電動推桿1的伸長量，l2為電動推桿2的伸長量。當升沉電動推桿停留在中點時，將正信號帶入到正逆運動學數學模型中可得，當縱搖角度為6°時，電動推桿移動量為10.45 mm。當橫搖角度運動到15°時，電動推桿移動25.89 mm。平臺角度與電動推桿的伸縮量的關系如圖4和圖5。

圖6展示了縱搖角度在0°位置和15°位置時，電動推桿以l2=36 sin((2πt)/8)運動時，平臺角度因縱搖方向改變，耦合作用導致的平臺橫搖角度的差別。實線是縱搖角度為0°時，電動推桿伸長時平臺角度。虛線為縱搖角度為15°時，電動推桿伸長時平臺角度。由此看出在本課題中平臺耦合對角度影響較大，在最大有2°左右的耦合影響。

在運動過程中，升沉運動對需要三個電動推桿完成運轉動作的同時對升沉運動的運動量進行補償。升沉運動占系統運動總功率中最大的一部分，其擺動和轉動直接影響到升沉電動推桿、橫搖電動推桿和縱搖電動推桿的伸長量和運動規律。升沉運動不僅僅只線性影響橫搖電動推桿和縱搖電動推桿的伸長量，由于升沉運動改變了橫搖運動和縱搖運動的桿長，電動推桿在推動平臺轉動時的伸長量也有影響。

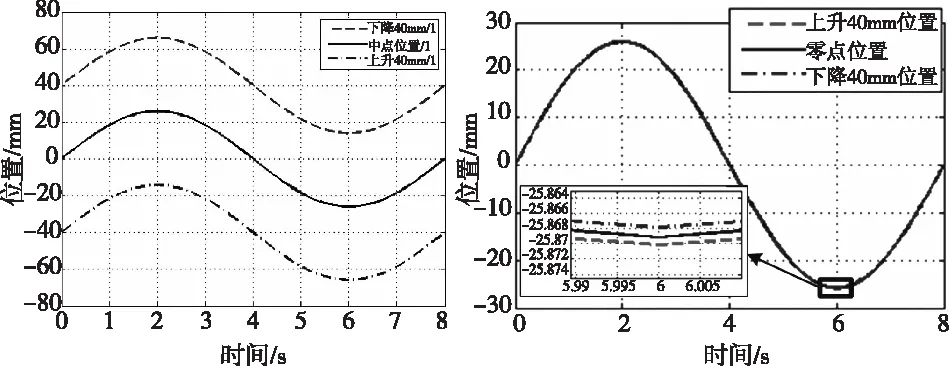
圖7 升沉運動影響曲線 圖8 耦合對轉動的影響

機構以周期為8 s幅值為15°的正弦信號進行運動時，升沉量為0 mm和正負40 mm對電動推桿的伸長量如圖7所示。升沉運動不僅僅只線性影響橫搖電動推桿和縱搖電動推桿的伸長量，由于升沉運動改變了橫搖運動和縱搖運動的四桿機構中的桿長，其對電動推桿在推動平臺轉動時的伸長量會產生影響。當升沉分別為40 mm、零點位置和-40 mm時，平臺轉動15°需要的電動推桿伸長量如圖8所示。可見機構運動處于小角度(±15°)范圍運動，升沉運動對角度的耦合最大0.002°。

因為系統的三個自由度之間相互耦合的影響。因此在建立系統時，需要將運動學方程導入控制器的算法中。對于高精度的穩定平臺來說，橫搖和縱搖間相互耦合較大，不可忽略。而升沉運動對平臺轉動角度的耦合較小，最大僅為7″。

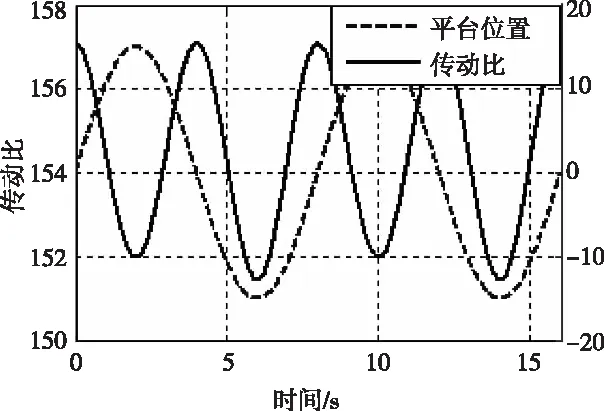
圖9 平臺位置對傳動比的影響

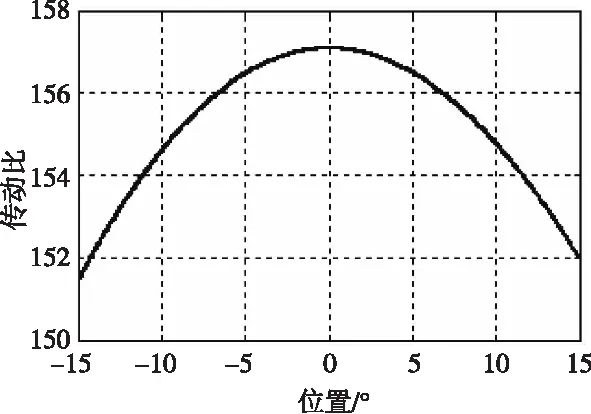
圖10 平臺位置與傳動比變化規律

電動推桿中，電機經過傳動比為1的齒輪傳動連接絲杠，則電機角度φ與電動推桿的伸長量l的關系為：φ=2·π·l/p，其中p為絲杠導程為4 mm。傳動比可以用電機端轉速除以末端平臺轉速得到。經過運動學的計算仿真，求得由電機端至平轉端的傳動比。當平臺以15°正弦進行運動可以看出，平臺在水平位置，即平臺和推桿垂直時，傳動比最大為157。在MATLAB中可以求到傳動比隨平臺運動關系曲線如圖9所示，平臺位置與傳動比的關系如圖10所示。

3 總結

針對一種三自由度并聯平臺進行了正逆運動學的計算，并通過simulink對其運動規律進行仿真計算。文中部分數據采用實際機構參數尺寸進行計算，得到的運動規律以及此種并聯平臺的運動特性，對特征相似的并聯平臺的研究有一定的參考價值。