基于分布式壓縮感知的窄帶LFMCW旋翼成像方法

, , ,

(空軍預警學院, 湖北武漢 430019)

0 引言

直升機旋翼旋轉作為微動的一種典型運動[1]，其雷達回波中包含著旋翼圖像等信息。研究窄帶雷達的直升機旋翼成像方法具有重要的軍事價值，因此這一問題引起了眾多學者的關注[2-5]。LFMCW雷達具有體積小、重量輕、功耗低等優勢，可用于小型預警裝備。但“走-停”假設在LFMCW雷達不再適用，必須考慮散射點的脈內運動，因此傳統的脈沖式窄帶雷達旋翼成像方法不能完全應用至LFMCW雷達中，需要研究針對LFMCW雷達的旋翼成像方法。

目前對于旋翼的成像方法可以主要分為兩類，一類是滿足方位采樣條件[6]的成像方法，如文獻[2]中利用基于層析投影算法對旋翼目標進行成像，文獻[3]中利用復數后向投影算法對旋翼進行成像，但這些方法在方位欠采樣條件下成像會出現虛假點。另一類是不滿足采樣條件的成像方法，如文獻[3,5-6]等方法中，運用到了壓縮感知(CS)理論來進行自旋目標成像；這些方法的共同特點是：首先假設轉速已知，然后提取出自旋目標所在距離單元的回波，構建相應的稀疏表示模型，最后稀疏重構從而對目標進行成像。當LFMCW雷達脈沖重復頻率較低時，會出現方位欠采樣的情況，此時采用滿足采樣條件的傳統成像方法會導致成像效果惡化甚至方法失效。而采用如文獻[3,5-6]中基于CS理論的方法雖然可以對旋翼進行成像，但這樣的方法存在兩方面問題：一是如果在信號脈壓后使用CS重構散射點，那么當旋翼上散射點線速度過大時，快時間二次項的變化將導致構建的稀疏基不準；二是如果在信號脈壓前使用CS重構散射點，那么只能逐一使用單個信號的稀疏特性進行重構，而后將所有信號的重構結果進行疊加，并沒有使用信號的聯合稀疏特性，從而在某種程度上損失了目標部分信息，導致了虛假點的出現。這些方法大都假設轉速已知，而實際中需要估計轉速。常見的窄帶雷達轉速估計方法有時頻分析方法[7]、正交匹配追蹤算法[7]、高階矩函數分析法[8-9]、自相關方法[10]等。這些方法存在多普勒頻率模糊、計算量大、低信噪比下成像質量變差等問題，其中自相關方法效率較高,具有一定低信噪比條件下的轉速估計能力，但是將它用于形狀規則的直升機旋翼轉速估計時，真實轉速與估計轉速存在著整數倍誤差，該誤差倍數等于旋翼對稱軸個數。因此，窄帶LFMCW雷達直升機旋翼成像方法和轉速估計方法有待進一步研究。

針對上述問題，本文結合自相關方法并充分考慮旋翼的形狀，首先依據搜索得到的轉速估計值對Dechirp后的信號構建聯合稀疏表示模型，然后通過分布式壓縮感知(DCS)方法進行散射點重構，最后將得到的成像結果分別計算熵值，最小的熵值即對應了最終轉速和成像結果。在算法性能上，一方面，由于算法利用了所有距離單元的回波信號以及高階相位項構建稀疏基，同時利用DCS方法進行重構，因此在低信噪比下具有較好的成像性能；另一方面，由于旋翼對稱軸個數是有限的，即最小熵的搜索范圍較小，所以本文方法具有較小的計算量。理論分析和仿真結果表明了算法的可行性和有效性。

1 窄帶LFMCW雷達旋翼回波建模

直升機葉片模型如圖1所示，假設對直升機旋翼回波已經完成平動補償，此時直升機等效為懸停狀態。將雷達、旋翼都投影到一個平面內，雷達到旋翼旋轉中心的距離為RC,旋翼上的散射點P到旋翼中心的距離為r，P點到雷達的距離為RP，P點以角速度ω繞C旋轉，初始時刻P點的初始旋轉角為θ。目標的旋轉中心C點位于x軸上，其初始坐標為(xC,0)。選取C為參考點，即Rref=RC。

圖1 雷達與旋翼關系示意圖

雷達發射窄帶LFMCW信號，旋翼目標回波[11]為

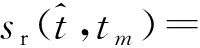
(1)

參考信號為

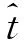
(2)

式中，τref為參考時間，τref=2Rref/c。對線性調頻連續波Dechirp后的回波[11-12]為

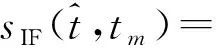
exp[Φ1+Φ2+Φ3+Φ4+Φ5+Φ6]

(3)

現有方法[3,5-6]中，當旋翼轉速較低時，Φ5，Φ6可以忽略。因此將式(3)變換至快時間頻域，可得到

(4)

式中，RP(tm)=RC+rcos(ωtm+θ)。對于窄帶雷達而言，脈壓后其回波集中在同一個距離單元內，不會發生越距離單元走動[7]，此時可以利用CS的方法對該距離單元的信號進行散射點重構。

實際上，當旋翼旋轉速度較高時，Φ5,Φ6不能忽略，此時式(4)中的相位信息會發生改變。此時稀疏基構建的CS成像方法失效，這是由于快時間二次項的系數是隨慢時間變化的，不能得到準確的脈壓表達式。因此無法利用CS方法對脈壓后的信號進行散射點重構，只能利用式(3)(脈壓前的信號)的相位信息進行散射點重構。但這樣將帶來信號利用不完全的問題，只能逐一通過單個信號的稀疏信息重構散射點，從而導致虛假散射點的產生。本文為了在高速旋轉下有效成像，充分考慮信號的聯合稀疏信息，建立準確的稀疏基，并結合分布式壓縮感知思想進行LFMCW雷達旋翼目標的成像。

2 基于分布式壓縮感知的窄帶LFMCW雷達旋翼成像

本節首先對LFMCW雷達的旋翼回波聯合稀疏性進行分析，并解釋可以使用DCS對散射點進行稀疏重構的原因；再依據假設已知的轉速信息(實際中轉速需要進行估計，本文將在2.3節提出一種估計方法)，構建聯合稀疏表示模型，最后利用DSOMP算法對旋翼散射點進行重構。

2.1 聯合稀疏性分析

從式(3)可以看出，旋翼的回波信息被分到了每一個快時間點上。對于不同的快時間，式(3)可以改寫為

sIF(n,tm)=exp[φ(n,tm)]

(5)

式中:φ(n,tm)=Φ1+Φ2+Φ3+Φ4+Φ5+Φ6；n為快時間的第n個采樣點，共有Nr個采樣點。式(5)可以進一步表示為

(6)

從式(6)可以看出，該信號可以等效為包含了Nr個散射點距離單元，對于這Nr個散射點距離單元而言，每個信號所攜帶的信息是相同的，它們都包含了葉片散射點的位置和幅度信息，具有方位向聯合稀疏特征。而DCS的思想是利用信號的聯合稀疏特性，不是只利用單個信號的稀疏特性對散射點進行重構。相比于CS只利用一個信號的稀疏特性的思想，DCS利用信號聯合稀疏特點的思想可以降低散射點錯誤重構的概率，使得虛假點減少。因此，對于方位向上欠采樣的信號利用DCS的思想可以得到完整的成像結果。如圖2所示，欠采樣矩陣中白色的方格代表有效數據，灰色的代表缺損數據；橫軸對應方位向慢時間，縱軸對應距離向快時間。從圖中可以看出,不同的快時間點對應著欠采樣回波矩陣的一個向量，該向量中包含著散射點的不同的幅度信息和相同的位置信息。而對于這總共Nr個散射點，它們包含的散射點位置信息都是相同的。例如其中某一個信號中包含著某散射點的位置信息，那么其他信號中也應該包含著該散射點的位置信息。通過這個思想，就可以利用信號的聯合稀疏性對旋翼進行成像。

圖2 聯合稀疏模型示意圖

2.2 聯合稀疏模型建立

首先將目標場景劃為維度N×Na的網格，其中在距離向上共有N個單元，在方位向共有Na個單元。式(3)中的ΔR=rcos(ωtm+θ),vr(tm)=rωsin(ωtm+θ)可分別表示為ΔR=xcos(ωtm)-ysin(ωtm)，vr(tm)=ω[xsin(ωtm)+ycos(ωtm)]，其中x=rcosθ,y=rsinθ，x,y是散射點在直角坐標系上的位置。然后對場景進行向量化處理，即令x=vec(X)=[σ1,σ2,…,σK,…]NNa×1，那么對于第n個快時間點而言，其回波的稀疏表示結果[6]為

Sn(m)=Ψn(m,ω)X+e

(7)

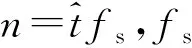
Ψn(m,ω)=exp[A1xkcos(ωmTp)+

A2xksin(ωmTp)]?

exp[A3ykcos(ωmTp)+

A4yksin(ωmTp)]

(8)

(9)

式中，X為待重構的圖像，||X||2,0為非零行的個數。由式(9)的構建過程可知，該過程與DCS理論相吻合[13]，因此式(9)可視為是一個DCS數學表示模型。典型的DCS重構算法有DSOMP[14]和DSP[15]等，本文采用DSOMP算法進行散射點重構。值得說明的是，重構完成后得到的矩陣維度為NNa×Nr，其中N為快時間的采樣點數。將該矩陣的每一列相加得到維度為NNa×1的向量，再將該向量按順序重新恢復為N×Na的矩陣，該矩陣就是重構的圖像。從式(9)可以看出，構建完整的稀疏基首先需要對旋翼轉速進行估計，然后再進行DCS重構，即可實現成像。

2.3 基于圖像最小熵的旋翼轉速估計方法

在本節的成像方法中，轉速信息是成像的關鍵參數，轉速估計的精度直接決定了成像的質量。自相關方法具有計算簡單、抗噪性能較好等優點，因此可以考慮使用自相關的方法提取直升機旋翼轉速[16-17]。首先提取出脈壓后目標所在距離單元的信號，然后求取自相關函數，如式(10)所示：

(10)

通過該函數可以求得轉速估計值：

(11)

但是，該方法沒有考慮直升機的旋翼葉片是對稱分布的。而旋翼的葉片數的正確估計有利于旋翼的成像。本文根據直升機的旋翼回波的特點，提出了一種基于窄帶LFMCW雷達同時估計旋翼目標葉片數和轉速的方法，描述如下。

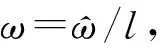
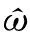
(12)

熵值越小代表圖像的聚焦效果越好。綜上，直升機旋翼轉速和葉片數估計步驟如表1所示。

表1 轉速估計算法

綜上所述，對應的成像過程算法如圖3所示。

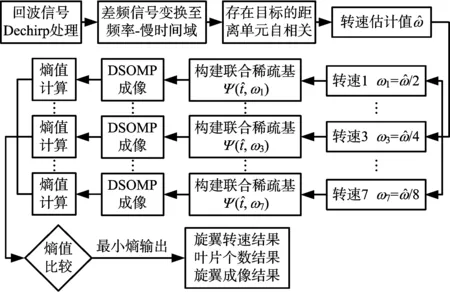
圖3 窄帶LFMCW雷達成像流程圖

本文方法在方位滿采樣和方位欠采樣的條件下均可實現對LFMCW雷達的旋翼目標成像，而這樣的效果是其他傳統方法所不能達到的，通過第3節的對比仿真可以看出本文算法的優越性。

3 仿真與分析

本文所有實驗都是在操作系統為Windows 7的個人計算機上實現的，仿真平臺為Matlab R2008b，計算機的主要參數如下：處理器為Intel酷睿E7500，主頻為2.93 GHz，內存為2 GB。仿真內容為基于DCS的LFMCW雷達的旋翼成像，直升機距離雷達20 km，轉速10π(31.42) rad/s，葉片長度為5 m，形狀為四葉片旋翼(對稱軸為4個)，直升機旋翼葉片散射點分布如圖4所示，散射點之間的距離間隔為1 m。

圖4 直升機旋翼模型

本文仿真內容中的噪聲為信號脈壓后添加的高斯白噪聲，信噪比定義為

(13)

3.1 窄帶LFMCW旋翼目標回波的時頻分布

設置仿真參數如下：發射信號為載頻1 GHz、帶寬1 MHz、時寬1 ms(重頻為1 000 Hz)的LFMCW信號。圖5(a)為旋翼在轉速為2πrad/s時的時頻分布，圖5(b)為旋翼在轉速為10π rad/s時的時頻分布。當自旋速度為2π rad/s時，此時最大的多普勒頻率為fdmax=2ωrmax/λ=418.88 Hz，滿足采樣條件PRF≥2fdmax。當自旋速度為10π時，fdmax=2ωrmax/λ=2 094.4 Hz，不滿足采樣條件PRF≥2fdmax，此時欠采樣倍數為2.09。

圖5是對旋翼回波時頻分析的結果。通過對比可以發現，在旋翼轉速較低時，低重頻LFMCW雷達可以通過時頻分析的方法對旋翼回波進行時頻分析，此時在圖5(a)中可以看到有清晰的“正弦”時頻曲線；但是在旋翼轉速較高時，低重頻LFMCW雷達就不能對旋翼回波進行時頻分析，此時時頻分析方法將會失效；從圖5(b)可以看出時頻分布圖已經模糊，對于傳統方法而言，只能對圖5(a)中的情況進行旋翼成像，對于圖5(b)中的情況算法將失效。本文所提方法不但可以對方位滿采樣條件下的旋翼目標進行成像，而且可以對圖5(b)方位欠采樣條件下的LFMCW雷達旋翼進行成像。

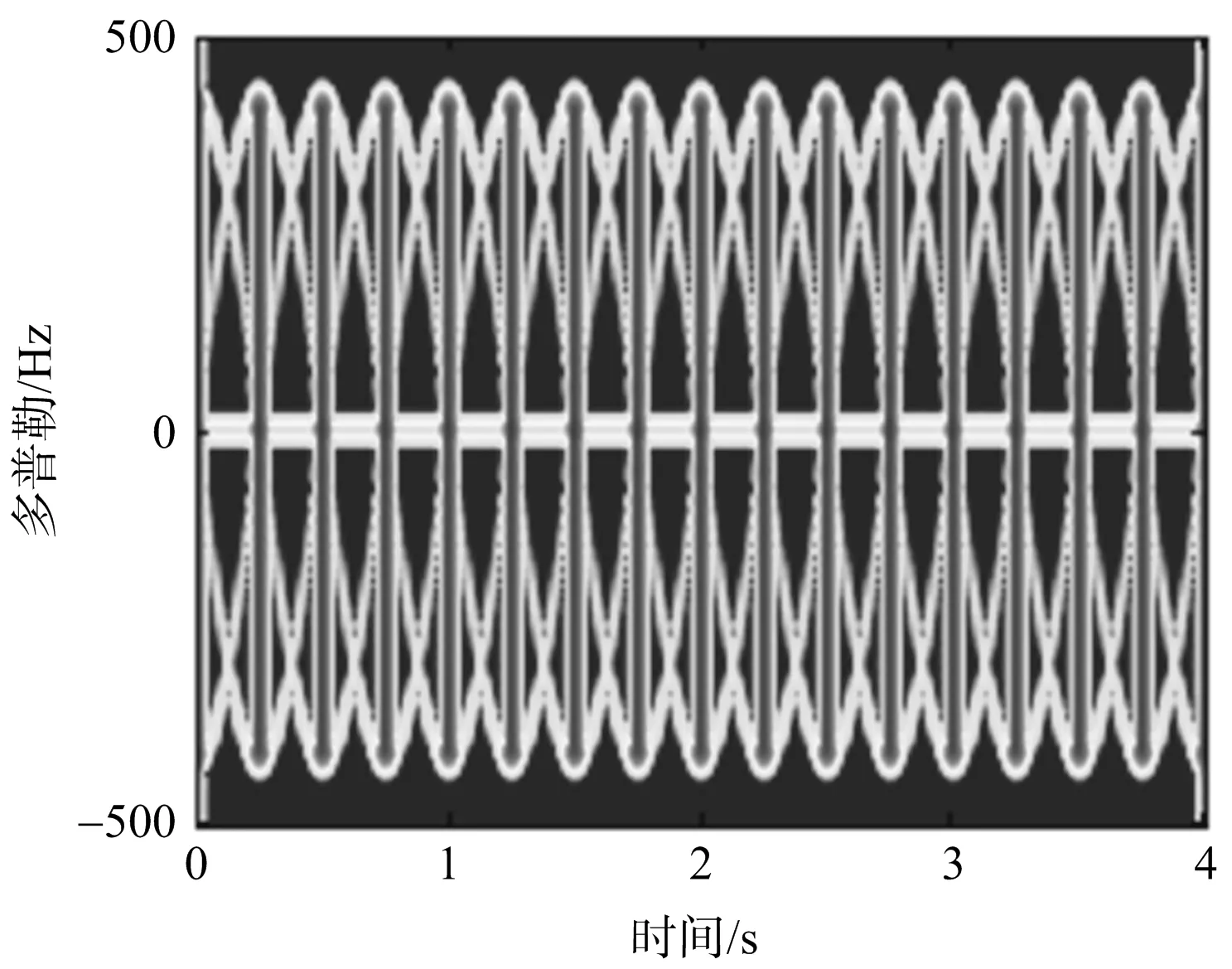
(a) 旋翼轉速為2π rad/s的時頻分布圖

(b) 旋翼轉速為10π rad/s的時頻分布圖圖5 旋翼在慢速旋轉和快速旋轉下的時頻分布圖

3.2 窄帶LFMCW的轉速估計

當觀測時間為0.5 s時，圖6是自相關的結果和圖像的熵值曲線。

從圖6(a)可以看出，由于旋翼葉片的形狀是規則的，此時出現的第二峰值距離中心峰值的時間為0.050 1 s，對應的轉速為125.41 rad/s。因此需要使用第2.3節中的方法，基于最小熵原理對旋翼可能的旋轉速度進行搜索，計算不同轉速下的熵值。如圖6(b)所示，當轉速為31.45 rad/s時熵值最小，此時對應的轉速就是估計的轉速。

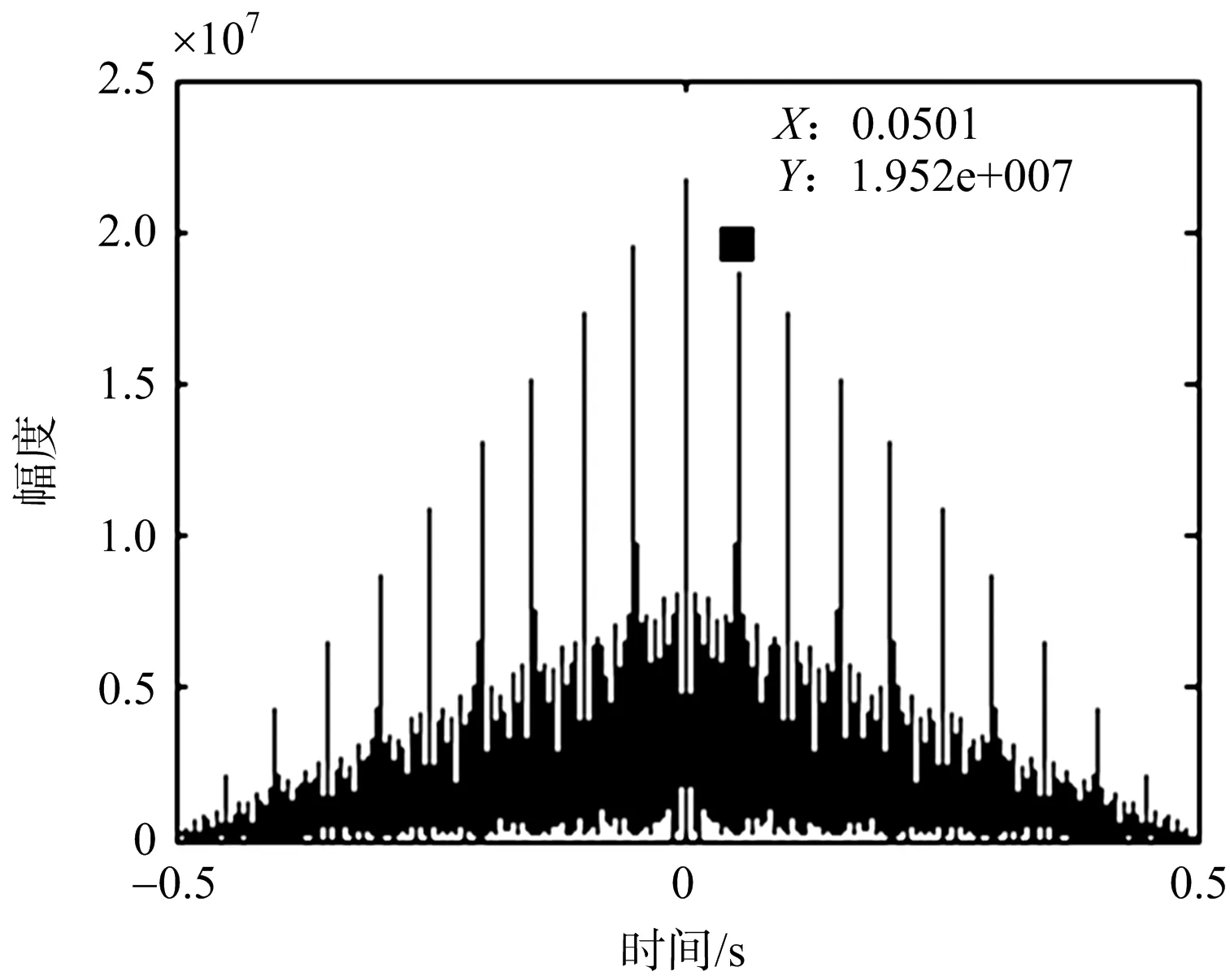
(a) 自相關結果

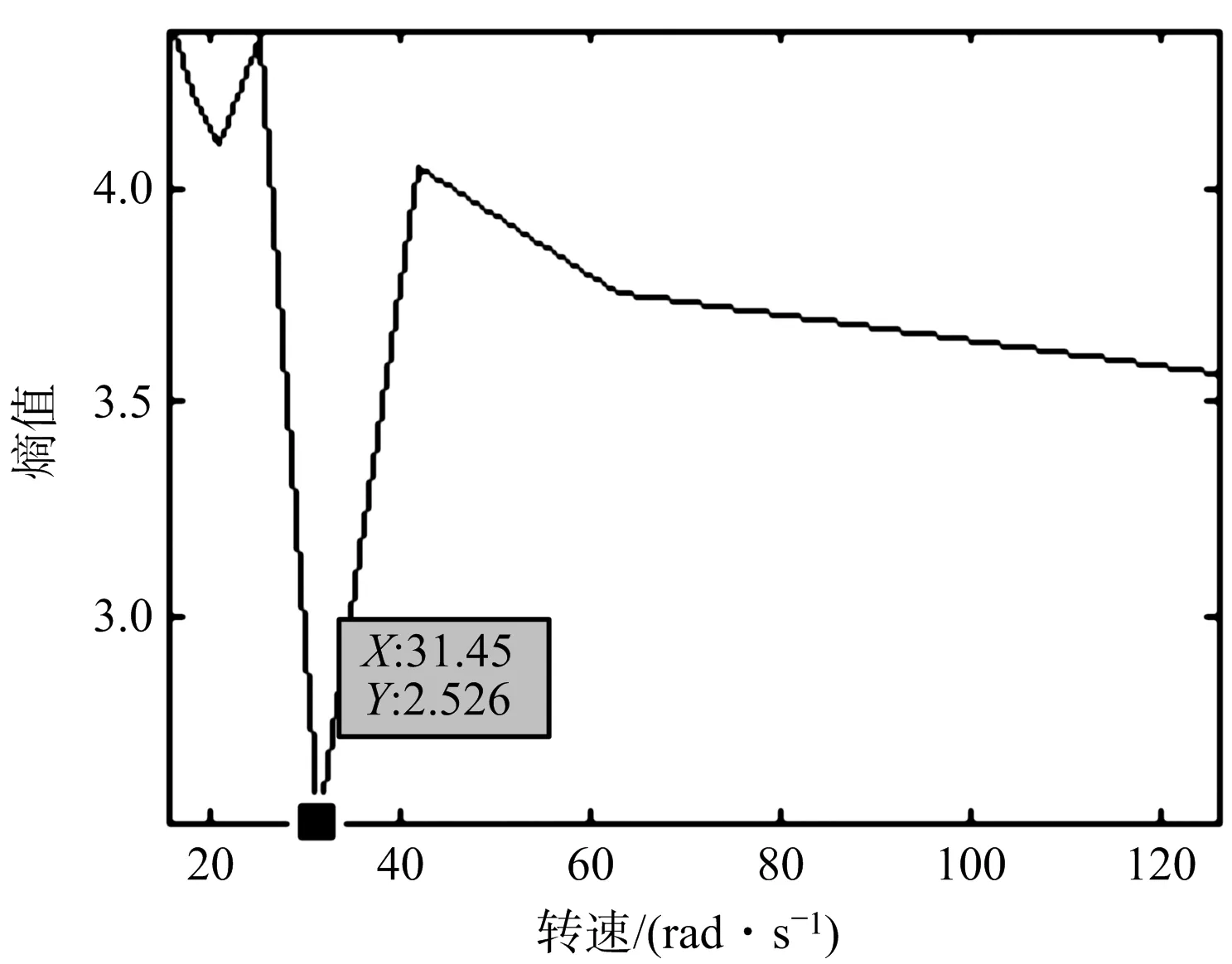
(b) 圖像熵值與轉速關系曲線圖6 轉速估計結果

表2分別在估計精度、算法時間、抗噪性能三個方面對比了本文方法、高階矩函數分析法(方法1)、正交匹配追蹤法(方法2)三種算法。需要說明的是，正交匹配追蹤算法由于計算量大、所需存儲量大，受計算機性能的限制，因此將轉速限定在[30 rad/s,40 rad/s]，步長為0.1 rad/s。

表2 轉速為31.42 rad/s的直升機旋翼估計方法對比

從表2可以看出，信噪比較高時，3種方法都可以估計出旋翼轉速，其中高階矩函數分析法精度最高，正交匹配追蹤算法次之，本文方法最差。但是隨著信噪比的降低，高階矩函數分析法精度變差，可以視為失效，而正交匹配算法和本文方法都較穩定。在運算時間上，高階矩函數分析方法時間最短，本文方法次之，正交匹配追蹤算法最慢。通過對比可以看出，本文方法可以在低性噪比條件下進行較快的轉速估計。

3.3 基于DCS的窄帶LFMCW直升機旋翼成像

仿真實驗的雷達參數與3.1節相同，下面將對比方法1(層析投影算法)、方法2(脈壓前CS方法)、方法3(脈壓后CS方法)與本文DCS方法分別在低速自旋和高速自旋以及不同信噪比條件下的成像效果。轉速為2π時的旋翼成像結果如圖7所示。

圖7 轉速為2π時的旋翼成像結果

圖7中所有成像結果的熵值如表3所示。

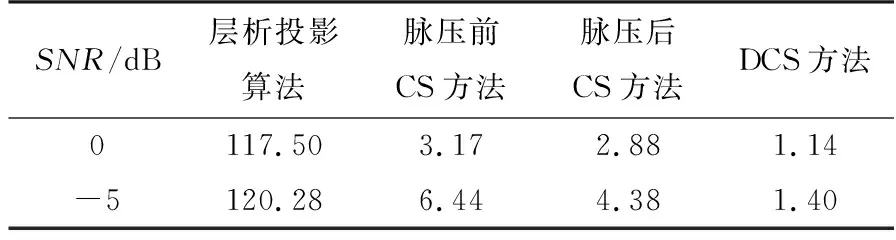
表3 不同算法成像結果對應熵值

轉速為10π時的旋翼成像結果如圖8所示。

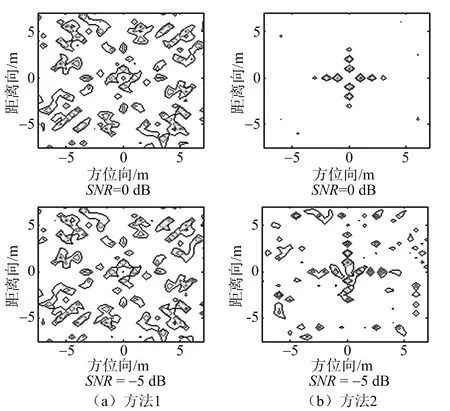
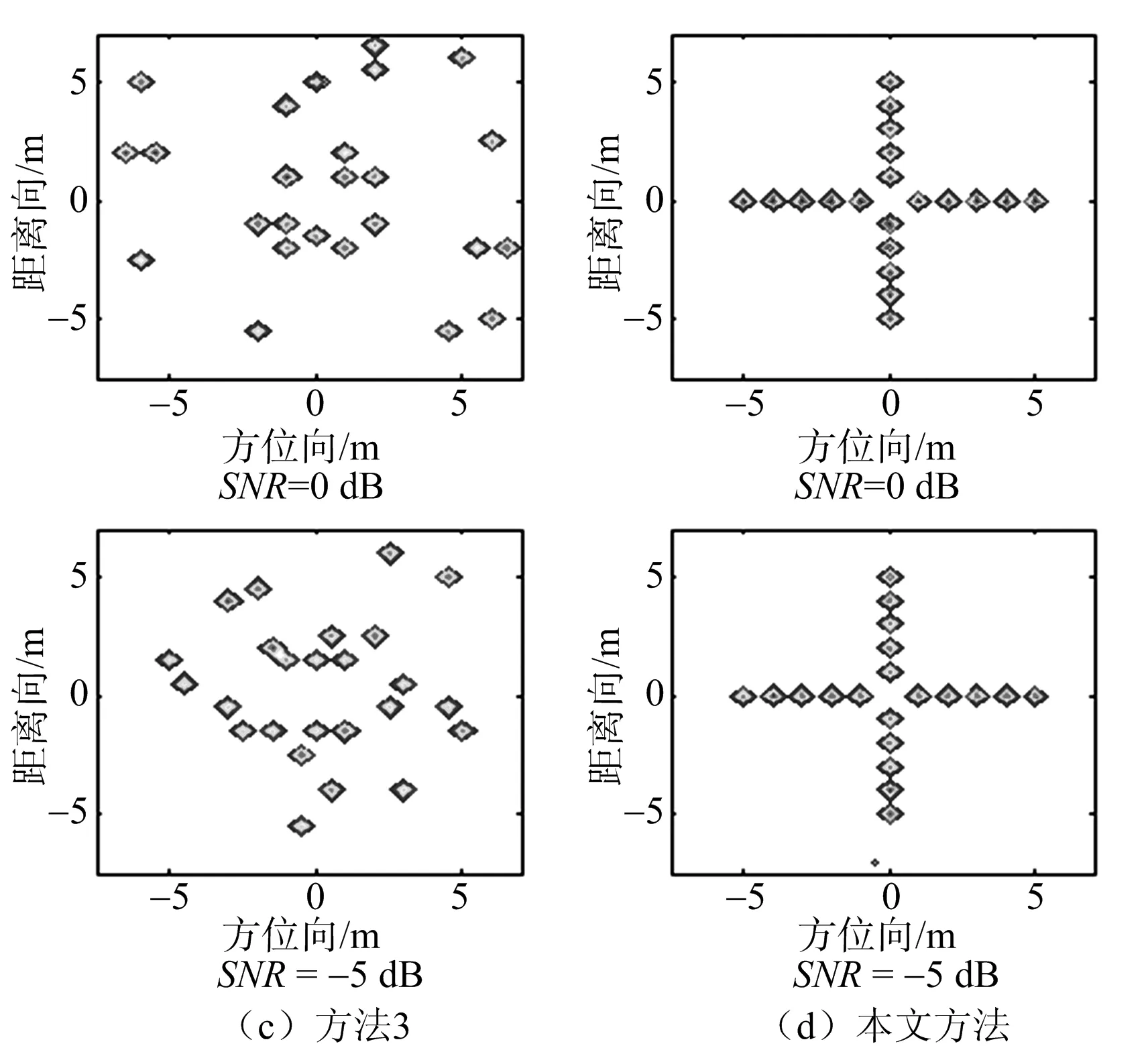
圖8 轉速為10π時的旋翼成像結果

圖8中所有成像結果的熵值如表4所示。

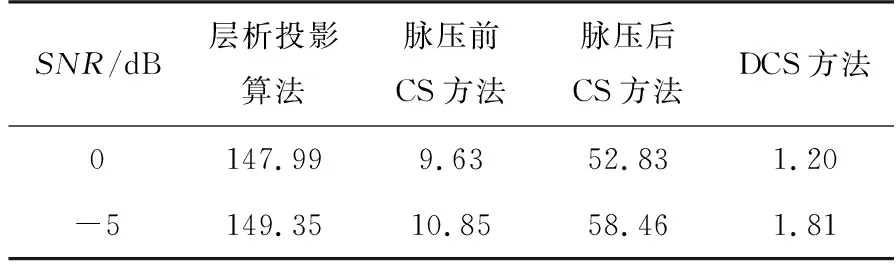
表4 不同算法成像結果對應熵值

從圖7可以看出，在轉速較低的情況下，4種算法都可以進行成像，但是層析投影算法的成像效果較CS成像效果較差，原因是層析投影算法散射點產生的旁瓣較高，對主瓣產生了影響。從圖8可以看出，當轉速較大時，方位向上采樣已不滿足奈奎斯特采樣定理，利用層析投影算法已經不能成像。脈壓后的信號使用CS方法成像也不能成像，這是因為在較高的轉速下構建的稀疏基不準確，不能匹配得到旋翼散射點信息，旋翼邊緣上的點已經不能成像。脈壓前的信號使用CS算法可以成像，但是由于CS方法只利用了單個信號的稀疏特性，此時重構時會產生一定數量的虛假點以及某些散射點的重構失敗。DCS方法利用回波信號的聯合稀疏性，恢復出了散射點位置和強度，對旋翼成像質量較好。

4 結束語

本文通過對窄帶LFMCW雷達旋翼的回波分析，得到了窄帶LFMCW雷達Dechirp后的回波信號。首先將信號脈壓并取出包含旋翼的距離單元信號，結合旋翼在形狀上是規則的實際情況，通過自相關和基于圖像最小熵的搜索方法估計出旋翼轉速和葉片個數，通過仿真驗證了本文方法具有在較短時間內對低信噪比條件下的旋翼轉速和葉片個數估計的能力；然后，本文提出了窄帶LFMCW雷達分布式稀疏表示模型，通過對Dechirp后的信號進行所有快時間點的分布式壓縮感知，較好解決了常規CS方法中存在的不能完全利用信號稀疏信息、稀疏基構建不準的問題。最后通過仿真驗證了該成像方法的有效性。