引入重疊度指標的FPPC油氣管道管段劃分方法

駱正山 王文輝 王小完 張新生

西安建筑科技大學管理學院

0 引言

由于油氣管道所經地區地域遼闊，環境復雜，會引起管道的自身屬性發生改變，進而造成管道沿線風險不斷發生變化。因此，要準確評估油氣管道各點風險值的大小[1-4]，需掌握管道沿線風險所具有的特征和規律，再構建合適的模型對管道進行合理劃分。

油氣管道完整性評價的研究成果頗多。孫寶財等[5]利用改進的BP算法對長輸油氣腐蝕管道失效壓力進行預測，Senouci等[6]分別采用回歸算法和人工神經網絡，基于歷史數據預測油氣管道的多種失效類型，但以上模型對樣本容量要求較高，預測結果精度較差。李大全等[7]采用模糊聚類對油氣管道進行劃分，張杰等[8]建立基于主成分—聚類分析法的油氣管道風險評價模型，然而模糊聚類法并不能針對具有特殊數據特征的管道樣本集進行精確劃分，推廣性不強。舒暢等[9]引入投影尋蹤聚類（Projection Pursuit Clustering，PPC）算法評估油氣管道的失效可能性，但該算法易受到指標維數的影響，當樣本指標維數過高，該算法在執行時會出現不穩定甚至失效的問題。綜上，現有方法均存在不同程度的局限性且對油氣管道的管段劃分缺乏系統理論依據，其劃分結果不理想、與實際吻合度不高。

模糊投影尋蹤聚類（Fuzzy Projection Pursuit Cluster，FPPC）算法是一種應用于水質評價、環境監測、洪災評估等領域能夠處理非線性、非正態高維數據的新算法[10-12]。管道沿線地理環境的復雜性導致管道失效往往具有突發性，即管道風險在空間上稀疏分布而在時間上密集分布，因此FPPC算法理論上適用于管段劃分。但傳統FPPC算法的投影指標函數只考慮到數據集的類間稀疏度和類內緊密度，實際應用中，管道樣本的數據類大小分布并不均勻，僅用所有樣本點到聚類中心的距離之和來刻畫管段樣本集中類的緊密度，難以識別數據集中的小類或低密度類，得出的最佳聚類數往往出現錯誤。

綜上所述，筆者構建了一種改進的FPPC算法管段劃分模型，建立管道劃分評價指標體系，引入考慮樣本重疊度的FPPC算法對管段進行動態聚類，通過聚類有效性評價指標評判聚類效果，得出最佳的管道聚類數，并根據類別離散值所確定的管道風險等級進行管段劃分，識別管道數據集中的小類。最后為了評價所提算法的性能，同時與PPC算法和傳統的FPPC算法進行了對比分析。

1 改進的FPPC算法及原理

1.1 模糊聚類迭代算法

將樣本集對于全體類別加權廣義歐式權距離的平方和最小作為目標，目標函數F表示如下[13]：

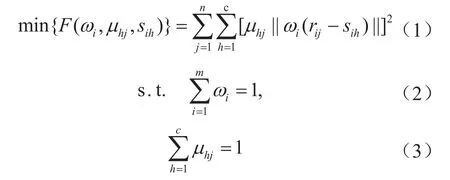
式中n表示樣本集的數目；ωi表示第i維指標所占權重；m表示指標維數；c表示類別數；sih表示指標i在類別h中的聚類中心；rij表示樣本j的第i個指標的歸一化值；μhj表示樣本j歸屬于類別h的相對隸屬度。

模糊聚類迭代（Fuzzy Clustering Iterative，FCI）算法的隸屬度μhj和模糊聚類中心sih表示如下：

式中sik表示指標i在類別k中的聚類中心，該算法的求解步驟可參見本文參考文獻[13]。

1.2 投影尋蹤聚類算法

投影尋蹤的基本思想就是將高維數據投影到低維空間，通過分析低維空間的投影特性來研究高維數據特征，是處理多因素復雜問題的統計方法[14]。投影指標函數一般定義為Q(a)=Sz*Dz，其中a表示單位長度矢量，Sz和Dz分別表示樣本投影值的標準差和局部密度，其計算公式及該算法的求解過程可參照本文參考文獻[12]。

1.3 引入重疊度指標的FPPC算法

本文參考文獻[15]中提出的投影指標函數考慮到類間的離散程度和類內的緊密程度，但現有研究表明，沒有一個投影指標函數能夠處理任何類型數據集且性能總能達到最優。因此，FPPC投影指標函數的設計要視樣本集的分布規律和屬性特征而定。考慮到油氣管道數據集中不同類樣本之間可能存在重疊的情況，筆者引入重疊度指標，將樣本點在兩個類之間的重疊度定義為超出給定閾值范圍外該樣本點屬于這兩個類的隸屬度差異，兩個類間的所有樣本重疊度之和定義為這兩個類的重疊度，這樣在保證了最小類間距離盡可能大和所有類都盡可能分離的同時，能夠發現管道樣本集中的小類或低密度類[16]。因此提出的投影指標函數能夠有效處理包含大小和密度差異較大數據類的管段劃分樣本集。

1.3.1 重疊度概念

重疊度度量因子（O）[17]定義公式如下：

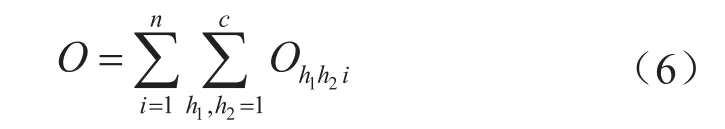
樣本xi在第h1類和第h2類之間的重疊度定義為：

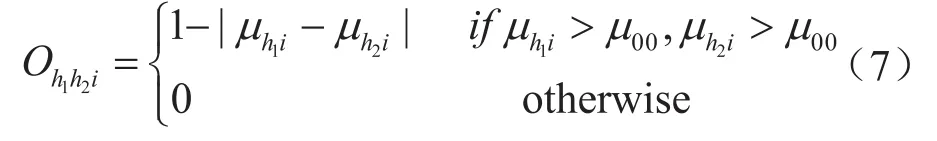
式中μh1i、μh2i分別表示樣本xi屬于第h1類、h2類的隸屬度；μ00表示重疊度閾值。

重疊度度量因子O構建的本質是：若樣本集中的某個樣本點對某兩個類的相對隸屬度都大于預定義的重疊度閾值μ00，則表明該樣本點距該兩類的距離都較遠，那么可認定該樣本對象是該兩類的重疊樣本。該樣本點到兩個類的隸屬度差的絕對值越小，則該樣本所在位置越趨向于這兩類的分界線處，即該樣本點對這兩個類貢獻的重疊度就越大[18]。

1.3.2 DOS投影指標函數的構建

綜合考慮投影點團間分布的稀疏度、重疊度和團內緊密度的DOS投影指標函數（QF）定義如下：

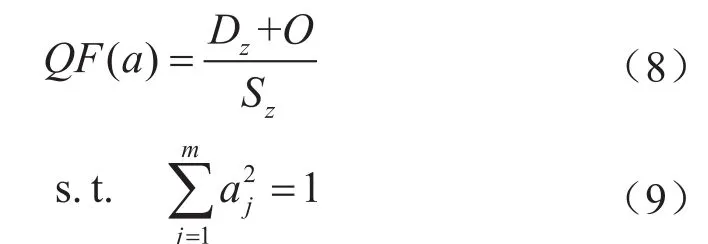
其中

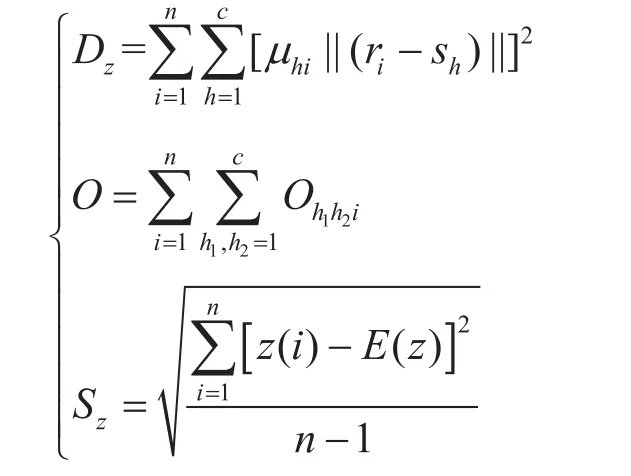
式中αj表示樣本的第j維投影方向值；ri表示樣本i的相對隸屬度；sh表示類別h的聚類中心；Dz表示類內樣本的緊密度；z(i)表示第i個樣本投影值；E(z)表示樣本投影值的均值；Sz表示類間距離，即投影點團間分布的稀疏度，該投影指標函數避免了密度窗寬參數的選取。

一個好的DOS投影指標函數應該使得類內緊密度和類間稀疏度都盡可能大，同時還需要滿足不同類間的重疊度盡可能小。因此，Dz和O越小，Sz越大，則DOS投影指標函數越小，即相應的模糊聚類劃分結果越優。以最小化DOS投影指標函數值為目標來計算最優投影方向向量。

1.3.3 改進的FPPC算法基本原理

改進的FPPC算法基本原理如下[19]：

1）首先運用投影尋蹤原理將高維樣本投影至低維空間，降低FCI的迭代運算量，避免多維指標出現聚類中心的交叉現象。

2）再利用FCI對樣本投影點進行模糊聚類，并將得到的最小歐式距離平方和來表征類內密度Dz，設定閾值，引入樣本重疊度指標O來表征類間的重疊度，構建DOS投影指標函數。

3）以DOS投影指標函數最小化為目標，對其尋優，找出最優的投影方向，進行投影尋蹤聚類。

通過以上措施，實現了類內密度Dz最小化的模糊聚類以及DOS投影指標函數最小化的投影尋蹤雙重迭代聚類，并通過DOS投影指標函數的構建來統一兩個模型的聚類目標。

2 改進的FPPC算法管段劃分模型

采用改進FPPC算法構建油氣管道管段劃分模型的基本架構如圖1所示。

2.1 管段劃分模型詳細流程

2.1.1 樣本集標準化

假設油氣管道風險指標的樣本集為{xij｜i=1, 2,…,n,j=1, 2, …,m}，其中xij表示樣本i的第j個指標值，n、m分別表示待評價管段數和油氣管道評價指標維數。按照下式采用越小越優的指標來標準化樣本集。

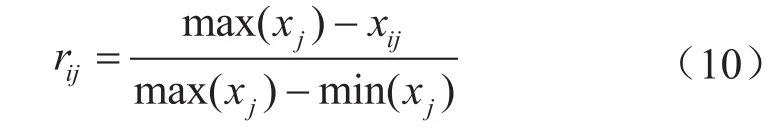
式中rij表示歸一化后的指標特征值；max(xj)和min(xj)分別表示第j個指標的最大值和最小值。

2.1.2 線性投影

筆者采用隨機函數初始化投影方向向量，用下式將油氣管道樣本集的多維空間投影到一維空間，計算出樣本投影值，隨機生成投影聚類中心向量。

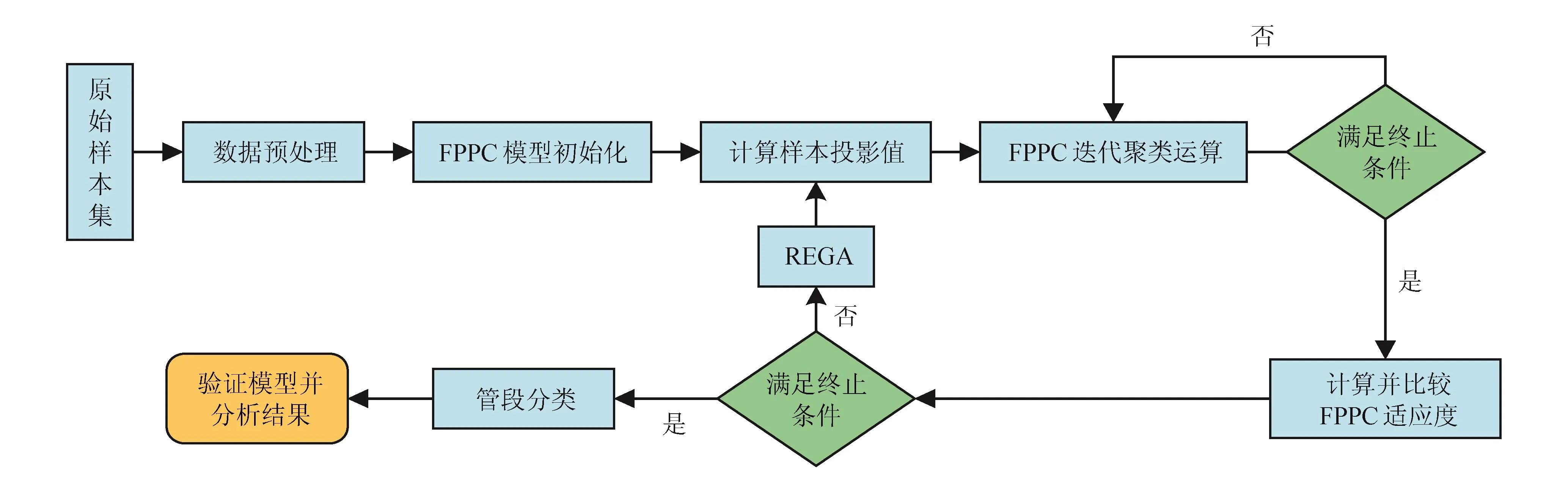
圖1 油氣管道管段劃分模型架構圖

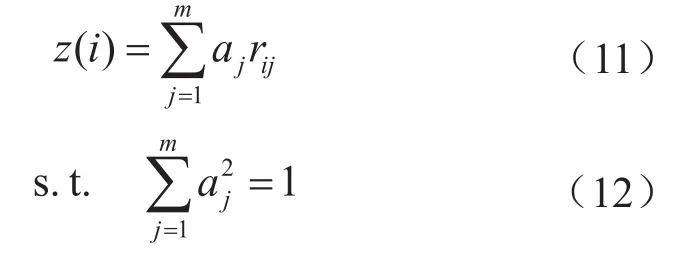
2.1.3 改進的FPPC算法迭代聚類

利用投影尋蹤技術將高維樣本集投影到一維樣本集后，權重向量降至一維，因此，ω的值為1，且sjh、sjk和rij分別變為sh、sk和ri，隸屬度μhi和聚類中心sh變為：

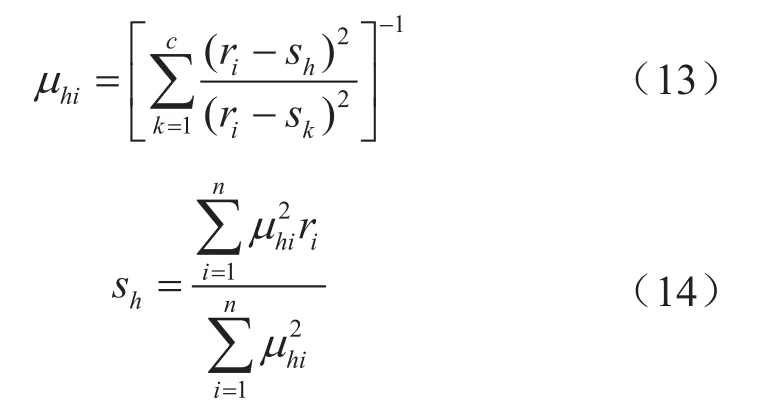
式中sk表示類別k的聚類中心，根據式（13）、（14）對投影點進行模糊聚類迭代運算，以式（8）中DOS投影指標函數最小化為目標尋找最優投影方向向量。采用基于實數編碼的加速遺傳算法（RAGA）來求解該優化問題[20]。

2.1.4 類別特征值的計算

參照本文參考文獻[21]提出對洪災大小進行排序的類別特征值法，可以求出管段各樣本的類別特征值C(i)。

式中h=(1, 2, …,c)表示類別值； 表示最優隸屬度。

對類別特征值進行四舍五入可得管段樣本所屬類別離散值，類別離散值對應油氣管段的相對風險等級，從而直觀得出聚類結果。類別離散值越大，則其所對應的管段相對風險等級越高，同時可根據類別特征值的大小對管段樣本的相對風險大小進行排序。

2.2 指標驗證

為了對模糊聚類效果進行評判，采用以下3種常用的聚類有效性指標函數[13]：

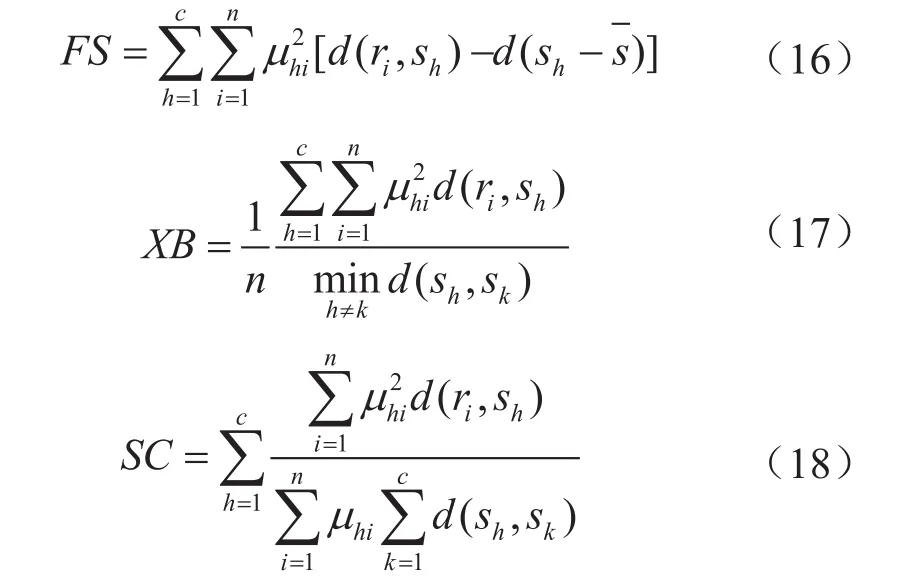
3 實例分析

3.1 油氣管道管段劃分指標體系的構建

國際管道研究協會（Pipeline Research Council International，PRCI）將管道失效事件分為22類，每一類都代表對管道完整性的一種威脅[22]。根據對油氣管道造成風險的對象不同，可將管道失效風險進一步歸類為自然因素、社會因素和管道自身因素3種。為此，筆者遵循客觀性、科學性和合理性的原則，結合我國的實際情況，參考美國《管道風險管理指南》[23]和本文參考文獻[24]，構建油氣管道風險指標的兩級層次結構（圖2）。

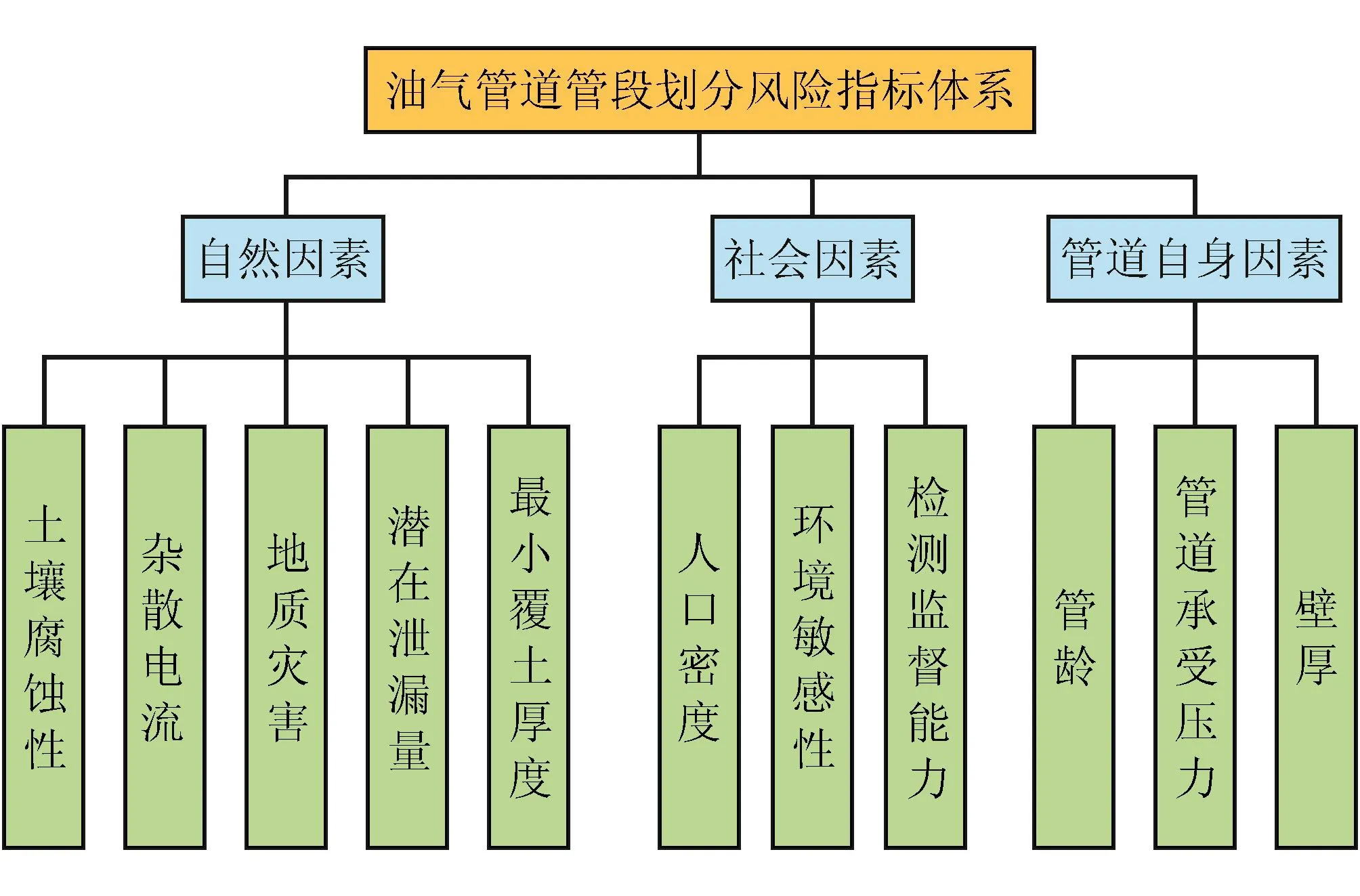
圖2 油氣管道管段劃分風險指標體系圖

3.2 數據準備

以我國西部某長輸氣管道為例，所評估的16段管道均為同一管道運營系統，輸送介質為天然氣，管道設計輸送能力為4.0×105m3/d，但各管段所處地理位置不同，管道沿線區域的自然、經濟和社會環境差異較大。根據圖2構建的油氣管道管段劃分風險指標體系，以及采集的現場數據，確定各指標的對應值，管道指標數據隨著距離的變化而改變，其部分數據如表1所示。

3.3 數據標定

由表1可知，管道風險指標值既有定性數據，也有定量數據，考慮到處理數據的方便性，可依據管道風險評價技術中風險等級劃分原則和參照表2的對應關系，量化底層指標，再結合實際情況，將表1中每個管道的屬性特征值都轉化為該指標對管道造成失效風險的定值（表3）。

3.4 驗證模型及結果分析

筆者分別采用傳統的FPPC算法和改進的FPPC算法對管道進行聚類劃分，并將兩種方法進行對比，利用本文2.2節中的聚類有效性指標來分析最佳的管段聚類數，并驗證算法的聚類有效性。FPPC算法的部分參數設定如下：樣本數為16，指標維數為11，適應度精度設為10－4，閾值設定為0.2。由管段劃分的實際意義，將聚類數分別設置為2、3、4、5和6，通過編寫目標函數和聚類有效性函數，結合加速遺傳算法搜索工具求解。不同的聚類數對應的聚類有效性指標值如表4所示。

分析表4結果可知，傳統的FPPC算法在聚類數設定為3時，各項指標值最小（即管段劃分達到最優），而改進的FPPC算法在聚類數為4時，各項指標值達到最小，且均小于傳統FPPC算法的各項指標值。因此，改進的FPPC算法對管段劃分更加準確。

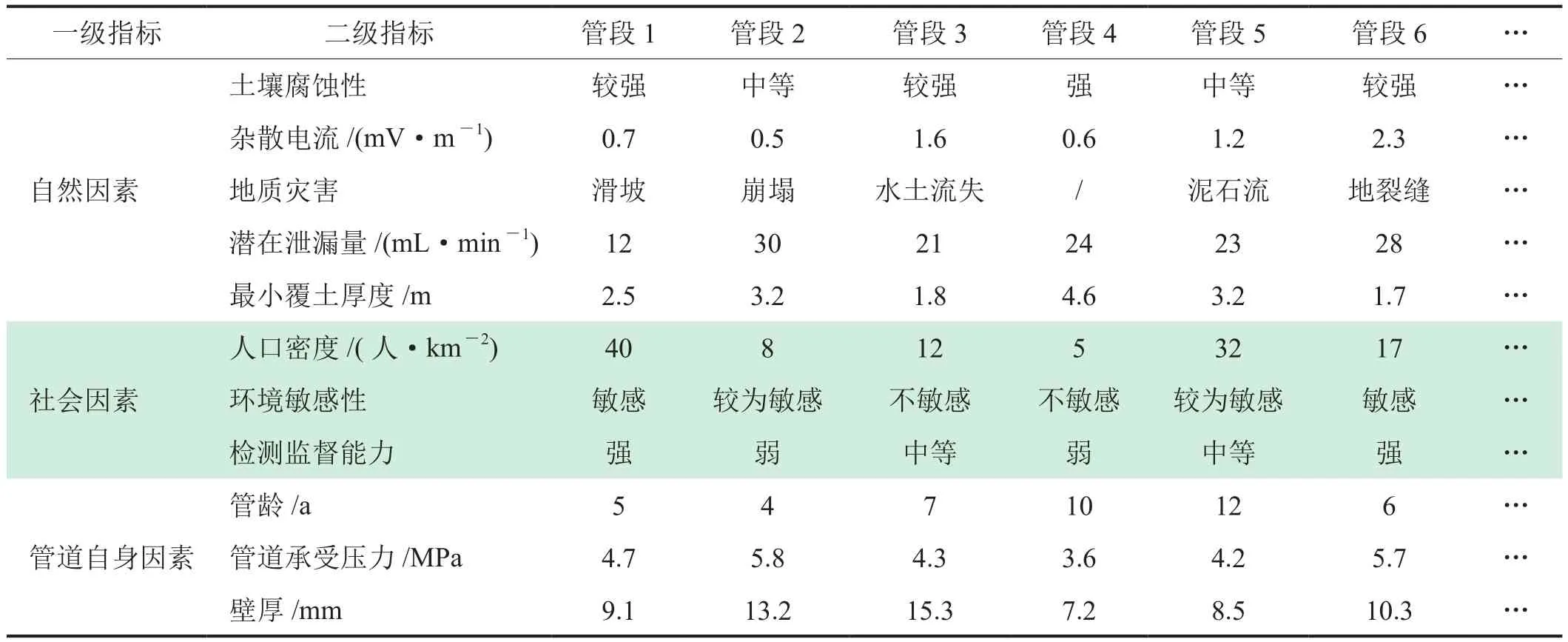
表1 管道實際屬性值表

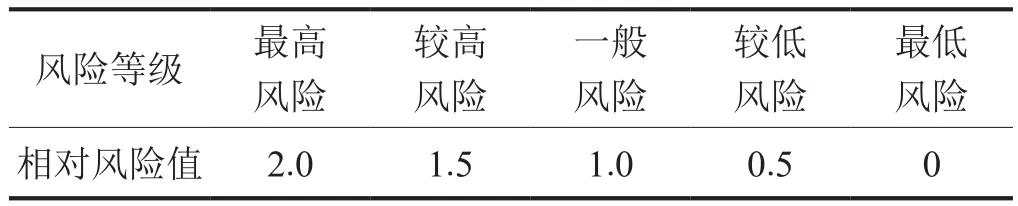
表2 指標對管道造成的風險等級表

當管段聚類數為4時，根據式（15），可求出管段相對風險等級。將管段相對風險等級定義為高風險（第4類）、較高風險（第3類）、一般風險（第2類）和低風險（第1類）。經改進的FPPC聚類，得到最佳投影方向為{0.254 1, 0.176 1, 0.325 2, 0.283 6,0.373 1, 0.351 8, 0.219 2, 0.547 6, 0.236 8, 0.127 9,0.186 7}，DOS投影指標函數最小值為0.075 3，各指標投影方向值的大小表明了該指標對管道風險的影響程度。投影值最優聚類中心為{1.786 0, 1.475 9,1.134 8, 0.723 4}，樣本投影值為{0.837 6, 1.114 7,1.524 3, 0.761 2, 0.774 1, 1.837 3, 1.662 5, 0.694 1,0.937 6, 0.858 3, 1.387 5, 1.616 4, 1.083 6, 0.792 3,0.714 3, 1.509 1}，最優隸屬度矩陣值如表5所示。

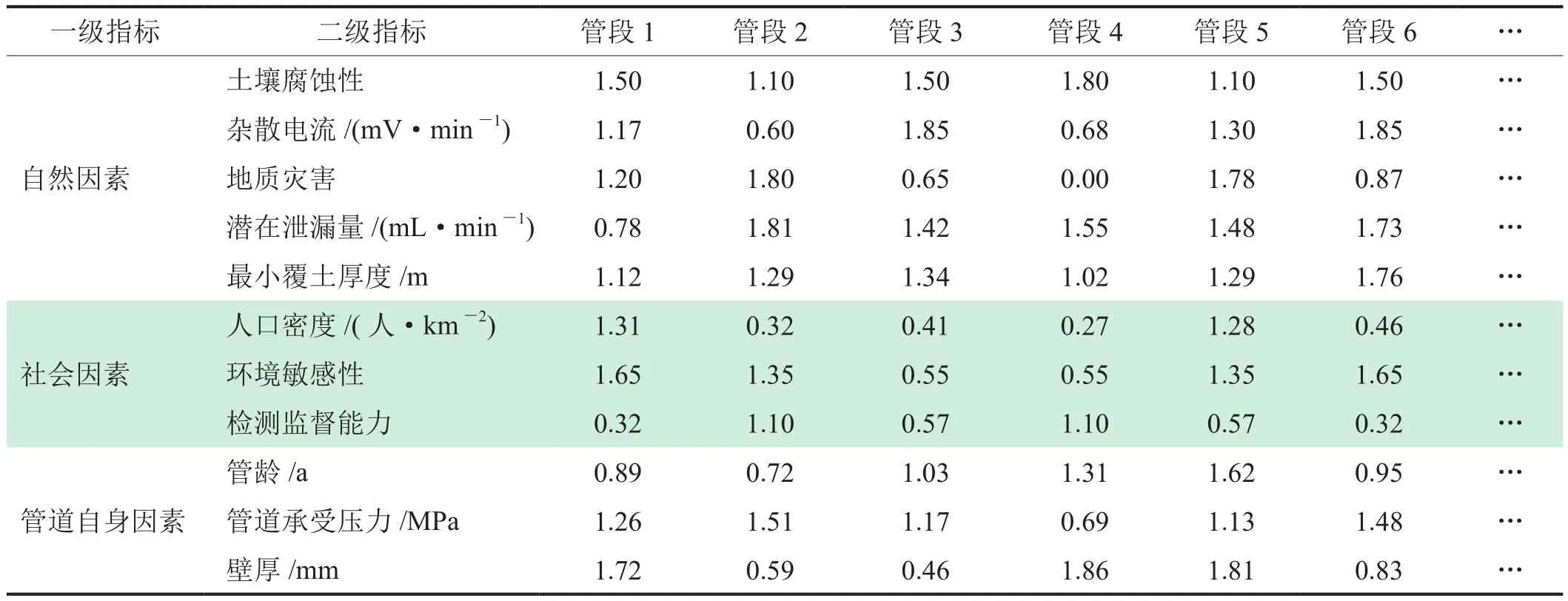
表3 指標的風險評分值表

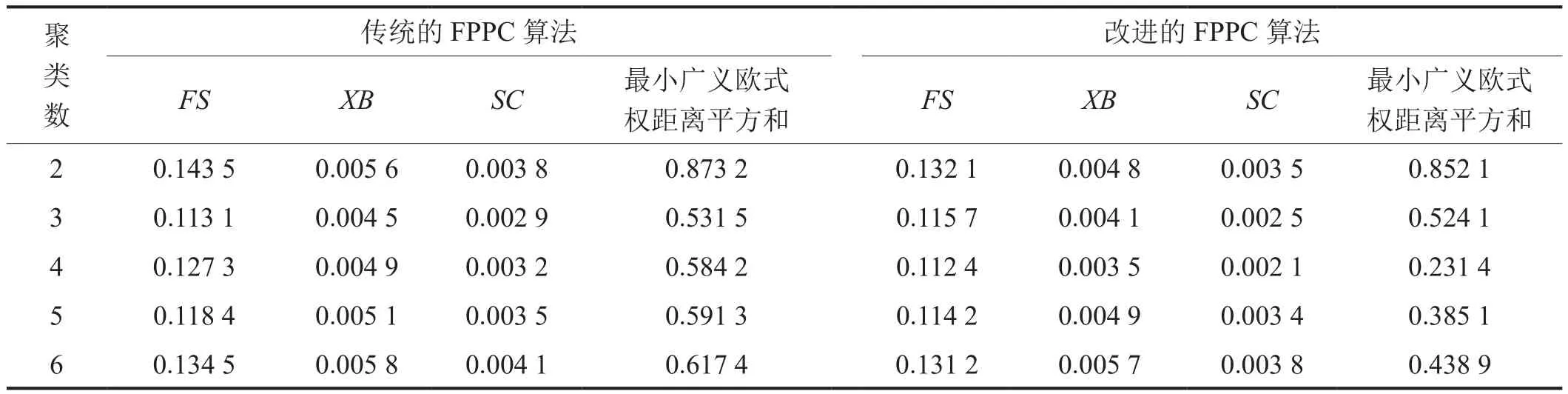
表4 管段聚類數和聚類有效性指標值比較表

為了能直觀看出改進FPPC算法能否識別出管道樣本中的小類，將傳統的FPPC算法最優聚類數為3時的管段劃分結果與改進的FPPC算法的計算結果進行對比。依據表5的FPPC類別連續值（限于篇幅，省略傳統FPPC算法的最優隸屬度矩陣），作出管段相對風險直方圖（圖3）。

由表5和圖3可知，傳統的FPPC算法將管道聚為3類，顯然是把管段6和管段7歸為第3類，但由圖3可知，管段6和管段7的類別連續值明顯偏離第3類，這會造成第3類聚類中心的極大偏移，從而導致聚類有效性指標值偏大，聚類結果具有較大誤差。而改進的FPPC算法將管段6和管段7歸為高風險類管段（第4類），有效識別出管段樣本中的小類。因此改進的FPPC算法的管段劃分結果更加合理準確。

對應用于管段劃分的聚類算法來說，雖然聚類的準確性是評價管段聚類效果的重要指標，但僅將聚類結果的準確性作為管段劃分效果的評價指標未免太過單一，其聚類的迭代次數及收斂速度也是評價管段劃分聚類效果的重要依據。為了比較引入重疊度指標對FPPC算法收斂性和迭代次數的影響，將改進的FPPC算法與PPC算法和傳統的FPPC算法進行30次的聚類迭代比較（圖4），PPC算法的密度窗寬選為常用的0.1Sz。

由圖4可知，3種算法的投影指標函數最小值雖然非常接近，但改進的FPPC算法的收斂速度明顯快于PPC算法和傳統的FPPC算法，且迭代次數更少，更快的接近于投影指標函數最小值。由此可知，改進的FPPC算法在收斂性和穩定性方面要優于PPC算法和傳統的FPPC算法。

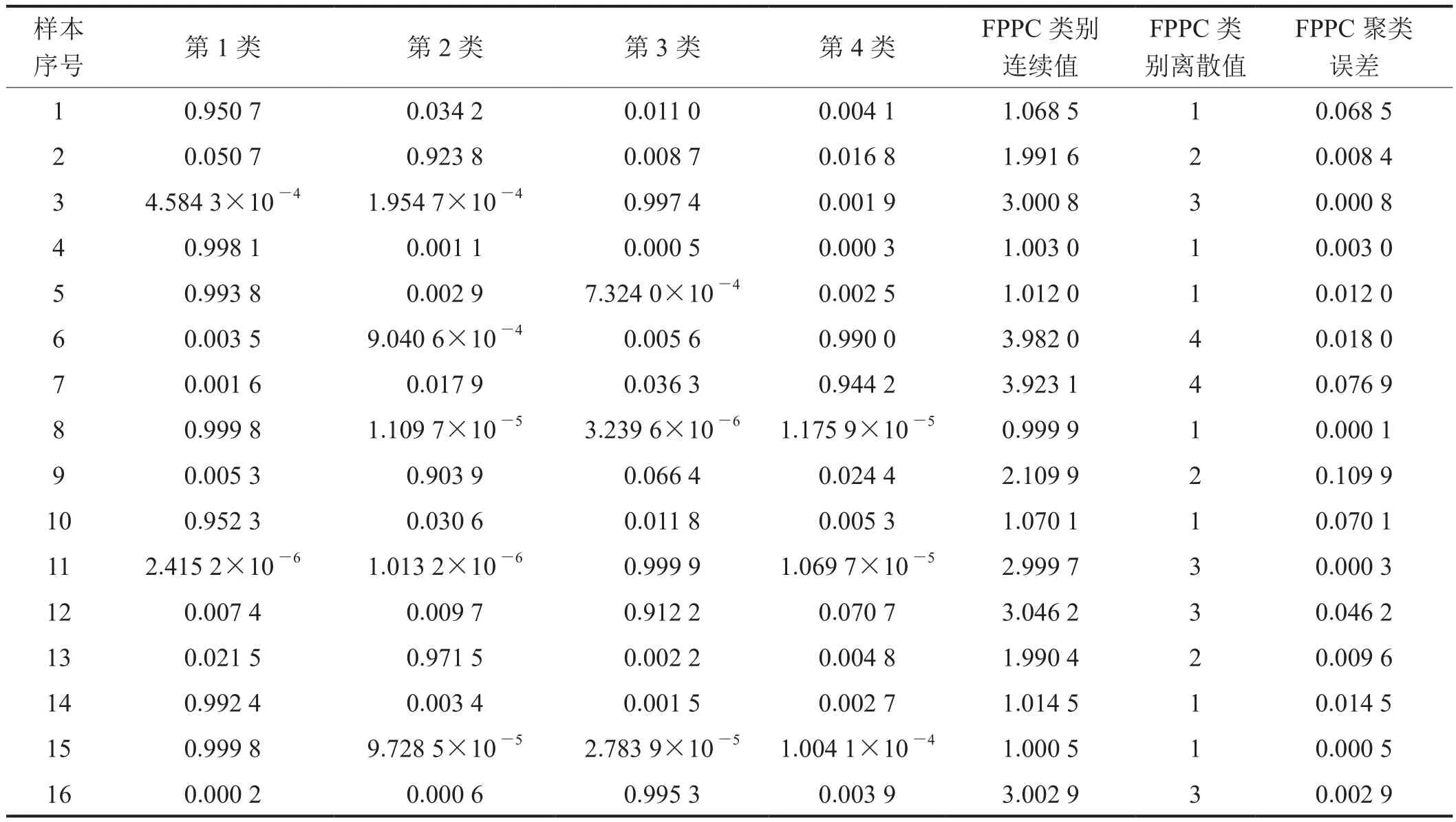
表5 最優隸屬度矩陣值表

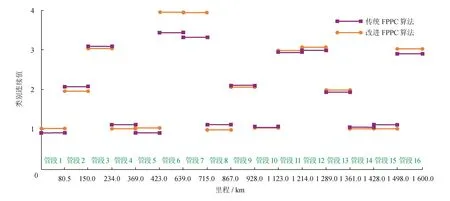
圖3 管段相對風險直方圖

4 結論

1）構造一種全新的DOS投影指標函數，針對管道失效風險的時空分布不均勻性，引入重疊度因子，該指標函數同時考慮到了投影點團內緊密度、團間稀疏度和重疊度的情況，可識別出管道樣本集中的小類或低密度類，保證了聚類結果的準確性和科學性。

2）改進的FPPC模型客觀地根據管道樣本集內在特性進行管道風險評價，在有無管道相應風險等級標準時均可對樣本集進行精確聚類并得到樣本類別連續值，聚類效果提高明顯，管段劃分結果更加客觀。

3）將改進的FPPC算法與PPC算法和傳統的FPPC算法進行對比，可知改進的FPPC算法具有更快的收斂速度和更少的迭代次數。因此，改進后的FPPC算法收斂性更好，穩定性更強。

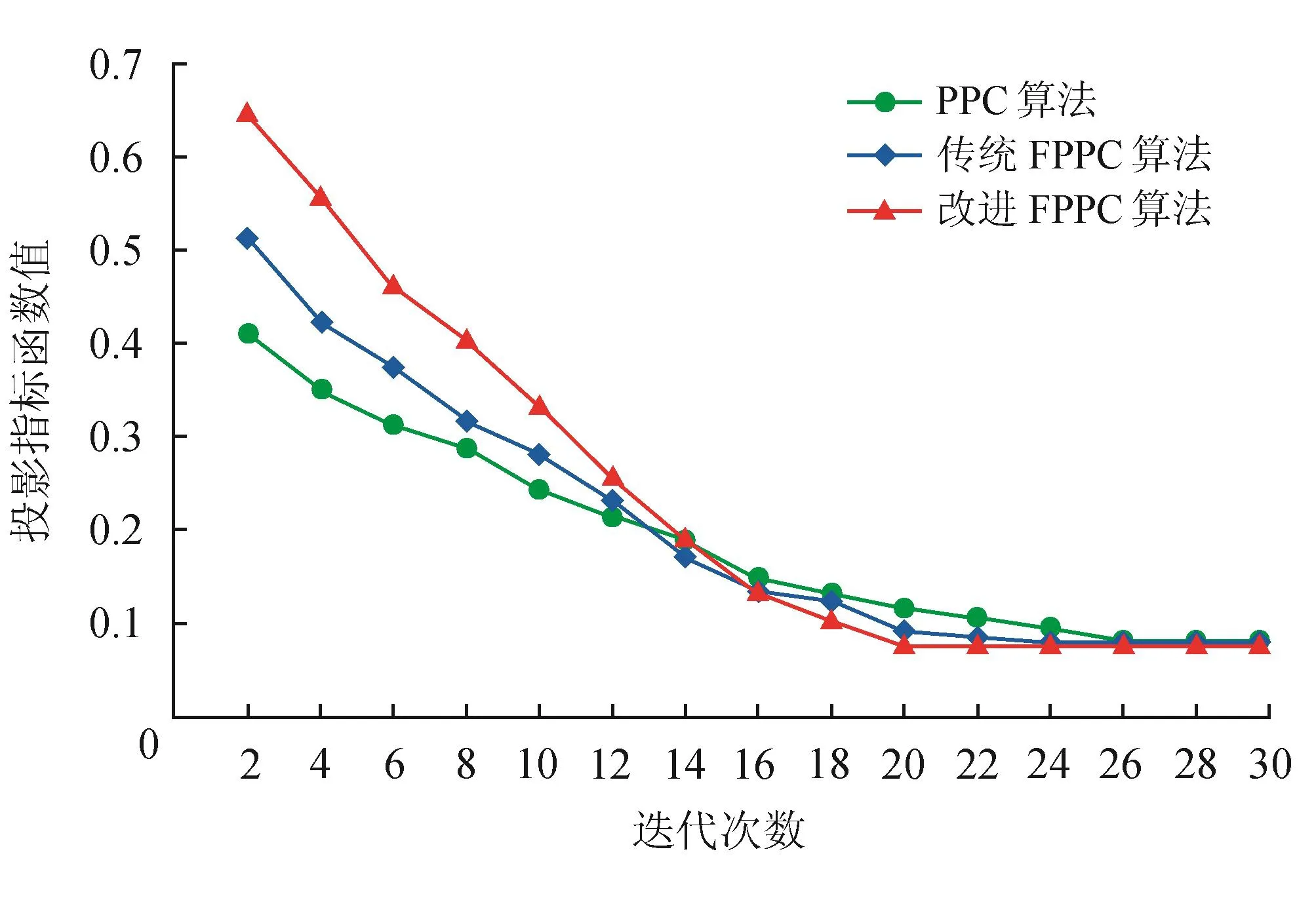
圖4 3種算法的收斂性比較圖

同時很多聚類算法受到多種參數的影響，如何更加合理地確定這些參數，比如閾值的選取，也是下一步研究工作的重點。