基于一致性算法的無人機協同編隊避障研究

張佳龍,閆建國,張普,王奔馳

(1.西北工業大學自動化學院,710129,西安;2.空軍工程大學航空工程學院,710038,西安)

相比單機而言,多無人機編隊具有很多顯著的優勢,其在軍事領域續航時間長、作戰半徑大、偵查范圍廣、作戰效率高、搜索能力強等,在民用領域可噴灑農藥、航拍、地形勘測以及空中加油等,因此受到很多學者的關注,成為研究的熱點[1]。目前,在航跡規劃[2-4]、協同編隊控制、信息共享和融合[5-7]以及避障等方面的研究已取得了一些明顯的成果,但大多數研究均是基于理論層面展開的,本文主要針對無人機編隊避障方面展開理論研究。

無人機編隊飛行,安全問題是首要考慮的關鍵因素之一,避障研究就顯得尤為重要。近年來,針對多無人機編隊飛行避障問題已提出許多控制算法,取得了良好的控制效果。控制避障算法大致分為基于優化的方法和基于規則的方法兩類。基于優化的方法采用模型預測控制(MPC)[8];基于規則的方法以人工勢場為理論基礎[9-10]。人工勢場方法不僅應用于無人機避障,還拓展到了自適應機器人導航,其基本原理是在設定的復合場中人工勢場力沿負梯度方向移動,本文基于這一原理,提出一種人工勢場避障方法,應用于無人機編隊控制。本文所提出的基于一致性算法對于單機和三機模型同樣簡化處理,主要突出算法無人機在三維空間中協同編隊避障控制方面的優勢,確保3架無人機組成的編隊能夠收斂于長機所設定的運動軌跡,同時在編隊中靠近障礙物內側的無人機與障礙物保持安全距離,即相對距離誤差收斂到較小的穩定值。本文的控制目標為3架無人機構成的正三角編隊隊形,無人機之間的網絡拓撲結構由已有文獻中的單向連接拓展為雙向連接,一方面每架無人機安裝有位置和姿態控制器,長機在既定的軌跡飛行,將編隊的飛行信息發送至兩僚機,僚機根據指令快速追蹤長機,形成正三角形編隊,防止與障礙物發生碰撞;另一方面,運用人工勢場的方法模擬電勢場,3架無人機構成三角形編隊,每架無人機處于動態平衡,一旦它們之間的相對距離小于平衡狀態的距離就會發生排斥,而它們之間的相對距離大于平衡狀態的距離就會吸引,使得無人機之間避免發生碰撞,達到避障的目的,同時確保編隊按照既定的隊形飛行。

文獻[11]中無人機編隊僅在水平面按照期望軌跡飛行,沒有在三維空間做編隊飛行,而本文控制算法能夠有效地在垂直方向避障,比前人提出的算法更加完善和靈活。將本文提出的基于一致性協同控制算法和應用人工勢場的方法應用到無人機編隊中,能夠同時在水平面和垂直方向進行有效避障。

1 問題描述

對于多無人機的協同編隊飛行,將一致性算法植入無人機控制器中[12-14],可有效避免無人機之間以及無人機與障礙物之間碰撞。下面采用雙向網絡拓撲結構建立三機編隊系統模型。

1.1 雙向網絡連接結構

圖論是多無人機編隊建模的數學工具,其中包含有向生成樹,在樹形結構雙向拓撲網絡連接中,任意兩點之間不產生閉合回路,每個無人機可以雙向傳輸各自的信息,實現分層管理。它的優點是擴充方便、靈活,易推廣到多無人機編隊,可靠性高。在無人機編隊避障過程中,長機在前,僚機在后,長機按照期望的路徑飛行,同時將飛行姿態和位置指令發送至僚機,僚機按照長機的指令飛行。在此過程中,長機將飛行指令發送至僚機,僚機接收指令調整姿態反饋至長機,同時僚機之間也通過信息交互,保持相對位置不變,這些都是雙向拓撲網絡連接,使得避障的可靠性增加。無人機編隊雙向網絡拓撲結構如圖1所示。

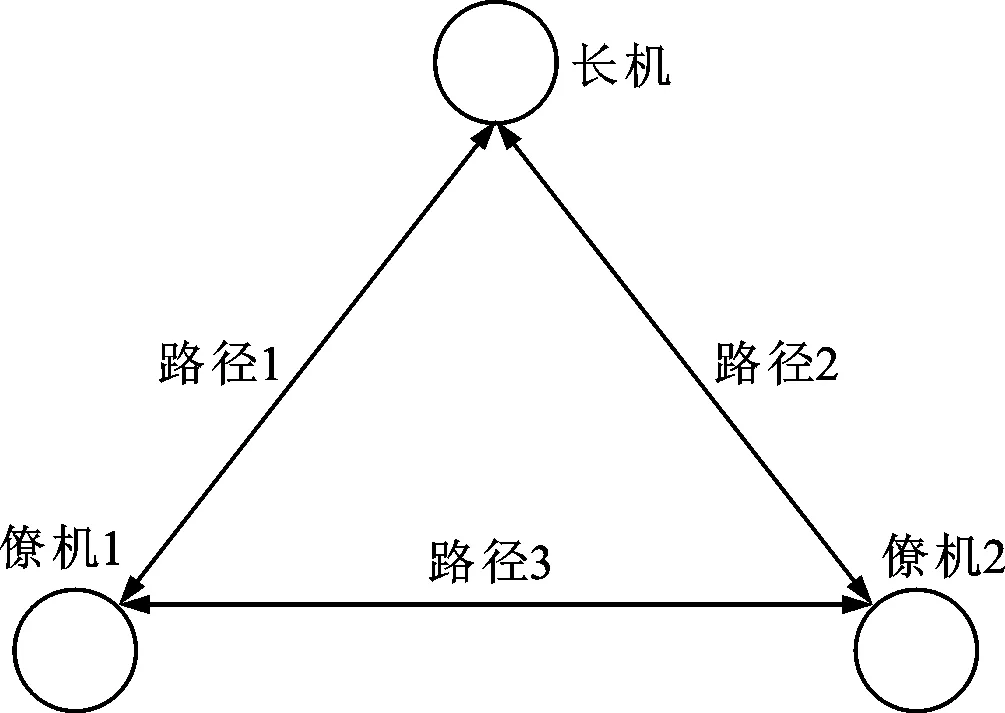
圖1 無人機編隊雙向網絡拓撲結構

由圖1可以看出,長機和兩架僚機以及僚機之間的通信均為雙向,即路徑1、路徑2和路徑3都是雙向通信。多無人機在編隊飛行、避障以及空中加油過程中,雙向通信有利于無人機編隊協同飛行完成各項任務。同時,當編隊中無人機數目擴充到N(N>3)架時,穩定性和可靠性均能得到改善。

1.2 定義控制目標

在3架無人機編隊系統執行一次作戰任務過程中,2架僚機之間、僚機與長機之間以及3架無人機與運動障礙物之間均未發生碰撞,且按照正三角形編隊飛行,都能夠收斂于時變的預期軌跡飛行,而時變預期軌跡由編隊的隊形決定,即長機所設定的軌跡。3架無人機構成的編隊系統,以長機為領航,兩僚機按照長機發送的指令追蹤直到集結為正三角形編隊隊形。為了能夠更好地控制無人機編隊以正三角形編隊飛行,做以下兩點假設:

(1)在網絡拓撲結構中,每架無人機均能夠接受來自長機發出的指令,同時兩僚機之間通訊也是暢通的,除此之外,在三機編隊模型網絡拓撲結構中,任意兩機之間是雙向聯系;

(2)長機的運動不依賴任何僚機,即長機運動不受任意一架僚機的影響,按照設定的軌跡飛行。

2 避障方法

多無人機編隊飛行時,為了防止機群之間以及單機與障礙物之間發生碰撞,避障方法顯得尤為重要。本文同時采用“長機-僚機”控制策略和人工勢場方法來防止無人機之間,以及無人機與障礙物之間發生碰撞。

2.1 “長機-僚機”控制方案

在編隊中,采用“長機-僚機”模型可以實現機動的靈活性和可控性,其控制模型如圖2所示。長機獲得地面指揮部發出的指令后,按照預期軌跡飛行,兩僚機保持與長機的相對距離和方向不變。在編隊中,考慮數據傳輸過載,使用雙向拓撲結構,而且每架無人機都被定義,長機與僚機以及兩僚機之間進行時效性通訊,這將有效地防止因通訊數據過大導致多無人機之間發生信息傳輸堵塞的現象。

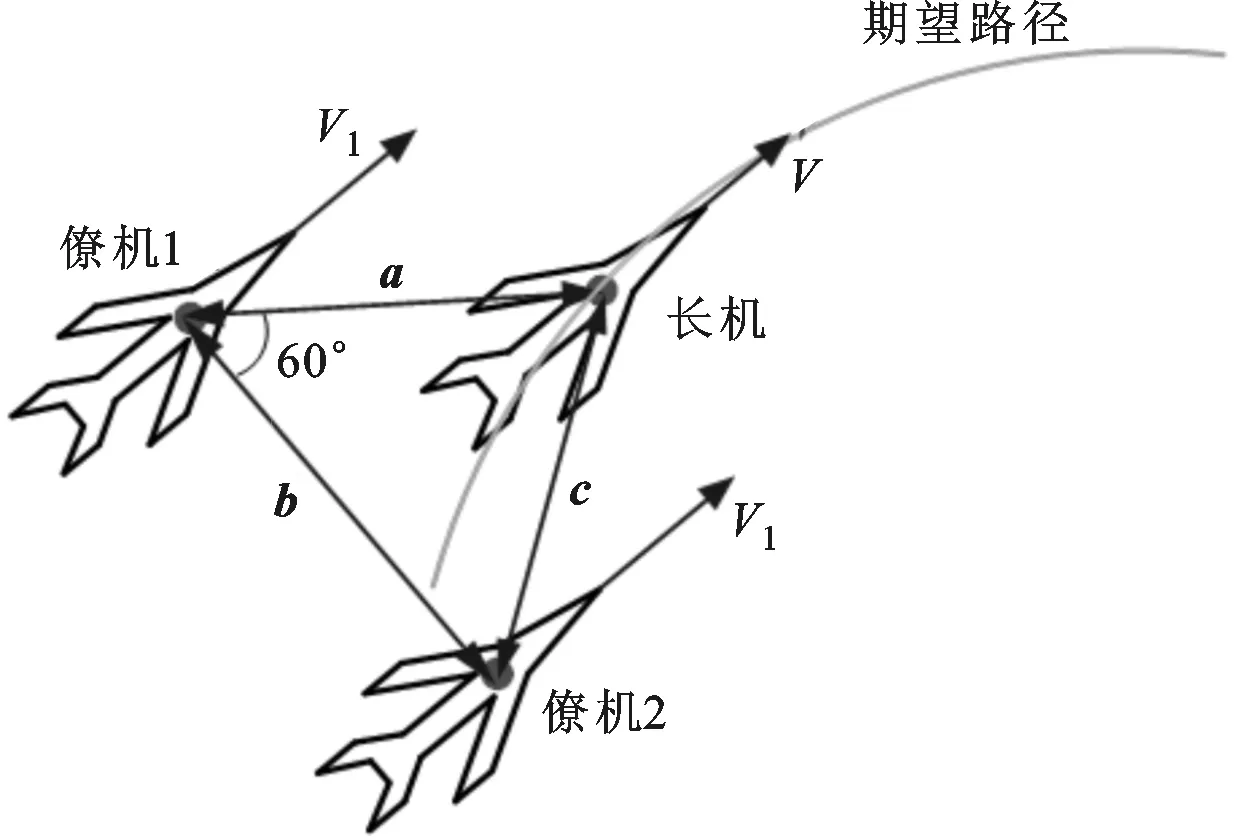
圖2 “長機-僚機”控制模式示意圖

根據以上分析,詳細的控制框圖如圖3所示。為了控制無人機編隊按照預期軌跡飛行,提出內外環兼容控制的兩種控制方案。外環的主要任務是控制每架無人機的位置、姿態、前行速度以及預期設定的軌跡。基于外環產生的控制指令,內環接受指令產生舵偏,副翼指令使無人機按照預期的高度飛行。本文集中于編隊控制,避免無人機之間發生碰撞,內環不作詳細討論,外環采用一致性算法。

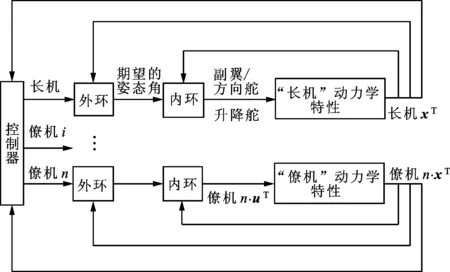
圖3 “長機-僚機”控制框圖

2.2 基于人工勢場方法

在無人機編隊系統中,由于3架無人機構成正三角形隊形,兩僚機與長機具有對稱性,因此選擇任意一架僚機(下文簡稱僚機)與長機作為研究對象,其編隊飛行避障示意圖如圖4所示。

圖4 編隊飛行避障示意圖

為了防止無人機之間發生碰撞,設定任意一架無人機的安全區域為以長機的質心為圓心、r為半徑、Δh為高度的圓柱體范圍。無人機在各自的安全區域內飛行,如果它們之間的安全區域發生重疊,此時應該采取規避機動,直到避開重疊區域。垂直方向僚機和長機的相對高度h與水平方向它們之間的相對距離lr的關系為

(1)

(2)

式中:rr、ra分別為機體坐標系和慣性坐標系下長機與僚機之間的距離;rl、rf分別為長機、僚機在機體坐標系中的位置。僚機與長機之間的人工勢場為

(3)

式中:Kh∈R是一個正實數的增益。由上式可知,如果僚機與長機在垂直方向互相遠離,則人工勢場減小,反之增大;如果僚機與長機的安全區域沒有重疊,則人工勢場為零。

由式(3)可得僚機與長機之間的平均勢場為

(4)

由式(4)可知,在多無人機編隊中,每架無人機產生的人工勢場總和為

(5)

針對本文的三機編隊系統,它們之間的人工勢場總和為

(6)

為防止僚機與長機發生碰撞,提出人工勢場力如下

fcai=-hUc,i∈{1,2,…,N}

(7)

式(7)沒有局部極小值,由于重疊區域內復合場僅由斥力場組成,其矢量形式如下

fca=-

(8)

人工勢場力沿著負梯度方向移動,即削弱這種場強作用,因此它的作用是使兩無人機之間的垂直距離范圍變大,達到避障的目的。

3 避障控制算法

3.1 無人機編隊避障

無人機編隊在整個飛行過程中,3架無人機構成的正三角形編隊隊形保持固定不變,且它們具有相同的前行速度,共同的姿態,共處于一個平面內,基于“長機-僚機”控制策略和人工勢場避障方法,編隊系統可以簡化為一個剛性質點,同時圓柱形障礙物可以簡化為一個圓,則無人機編隊系統避障問題可以簡化成一個質點繞過一個圓,且不與之相切。不論障礙物是靜止還是運動,質點與圓的相對關系要確保是相切或是相離,以避免發生碰撞,其示意圖如圖5所示。

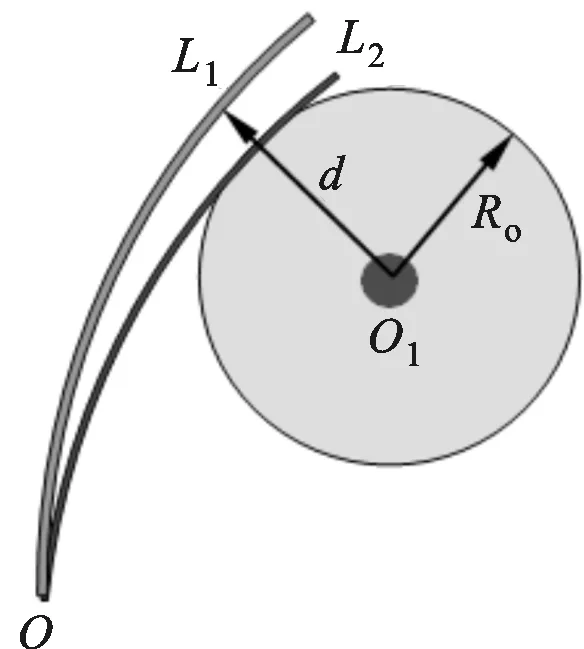
O表示無人機系統;O1表示障礙物幾何中心;L1、L2分別表示無人機系統在t1、t2兩個時刻的軌跡圖5 無人機避障示意圖

無人機系統與障礙物之間的關系為

|d-Ro|≥0

(9)

式中:Ro為障礙物的半徑;d為無人機在軌跡L1上與障礙物中心的相對距離。

地面指揮部控制編隊滿足式(9)的關系,即可避免無人機編隊與障礙物發生碰撞,實現避障目的。

3.2 無人機之間避障

3架無人機構成的編隊系統組成被控對象,即控制目標,針對控制目標之間在三維空間編隊飛行的避障,采用控制算法在水平面和垂直方向進行有效控制[15]。為了在無人機之間進行有效的避障,采用一致性算法使無人機編隊之間在垂直方向采取規避機動,而在水平面按照控制指令進行正三角形編隊飛行。本節主要考慮采用一致性算法在垂直方向且障礙物是運動情形下的避障研究。

無人機在垂直方向編隊飛行時,可將被控對象分為兩類:一是3架無人機構成編隊系統作為控制體;二是將無人機編隊系統的每架無人機看成控制對象。應用一致性協同算法實現控制體的協同編隊飛行,保持隊形不變;應用“長機-僚機”控制策略實現每架無人機集結后成編隊飛行。在編隊中,長機直接與兩僚機保持聯系,發送當前位置和期望位置指令,確保僚機調整姿態和速度,追蹤長機呈正三角形編隊。本文控制算法的優勢在于,編隊無人機拓撲結構是雙向連接,它們之間的信息傳遞時效性強,可防止因單機傳輸信息量過載發生堵塞現象。

無人機編隊中,無人機i的控制律如下式所示

(10)

(11)

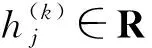
本文提出的無人機編隊避障控制算法的避障能力如下式所示

(12)

式中:ffromi表示在垂直方向編隊飛行的控制算法的避障能力;fcai表示人工勢場避障算法的避障能力。

引理假設多無人機編隊系統為由一架長機和N(≥2)架僚機構成的線性化模型,且滿足假設(1)(2)。控制算法(式(10))中γk為正的增益,且k∈{0,1},同時式(3)中控制參數kh為正實數,均滿足每架無人機。

證明對于每架無人機應用控制算法(式(10)),可以得到下式

(13)

(14)

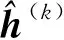
(15)

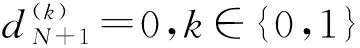
(16)

(17)

已知矩陣M,方程(16)可簡化成如下矩陣形式

(18)

式中:IN∈RN×N表示N維單位矩陣;0N∈RN表示N維零向量。

首先求微分方程(18)的解,通過解的特征來研究其穩定性。方程(18)對應的其次微分方程的解為

(19)

此處構建李雅普諾夫函數V,其由多無人機(本文為3架無人機)編隊系統總能量構成,表達式為

(20)

將V對時間求導可得

(21)

由式(7)可得

(22)

聯立式(21)和(22)可得

(23)

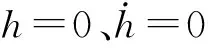
當兩架無人機之間的安全區域沒有重疊情形下,微分方程(18)的特解可以表示為

(24)

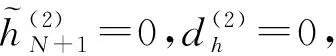
綜上所述,微分方程(18)的通解等于其對應的其次方程的通解加上本身的特解。因此,當控制增益γk和人工勢場表達式中Kh選擇合適的正值時,則方程(18)漸進收斂于

當t→∞

(25)

這是來自長機指令的收斂結果,根據式(25)任意一行元素,可證明在縱向每架無人機具有的避障能力將會使其收斂于期望的預定軌跡,構成正三角形編隊。

4 仿真實驗及分析

4.1 初始條件設置

通過仿真實驗驗證所提避障算法的有效性,需要做以下3個方面的假設:

(1)障礙物的運動速度和前行的方向是恒定的;

(2)在編隊飛行中,長機的姿態和位置都是通過地面指揮所發出的指令;

(3)長機與僚機之間的通信是同步的。

無人機的對地速度和障礙物的運動速度為56 m/s,每架無人機的質量為90 kg,俯仰角速率的極限值為10 (°)/s,偏航角速率極限值為10 (°)/s;在垂直方向,為了滿足建模和仿真的所有條件,編隊的控制增益和避障控制參數分別設置為γ0=1.5、γ1=3、kh=5.5,每架無人機的安全區域圓柱體高度ΔH=3 m、橫截面半徑ΔR=3.5 m。在垂直方向,無人機之間的高度差小于1.2 m,同時在水平面內無人機之間的相對距離小于10 m,無人機之間通過植入的算法計算,進行避障。

4.2 實驗結果

基于仿真的初始條件和假設,3架無人機編隊避障仿真圖如圖6～圖8所示。

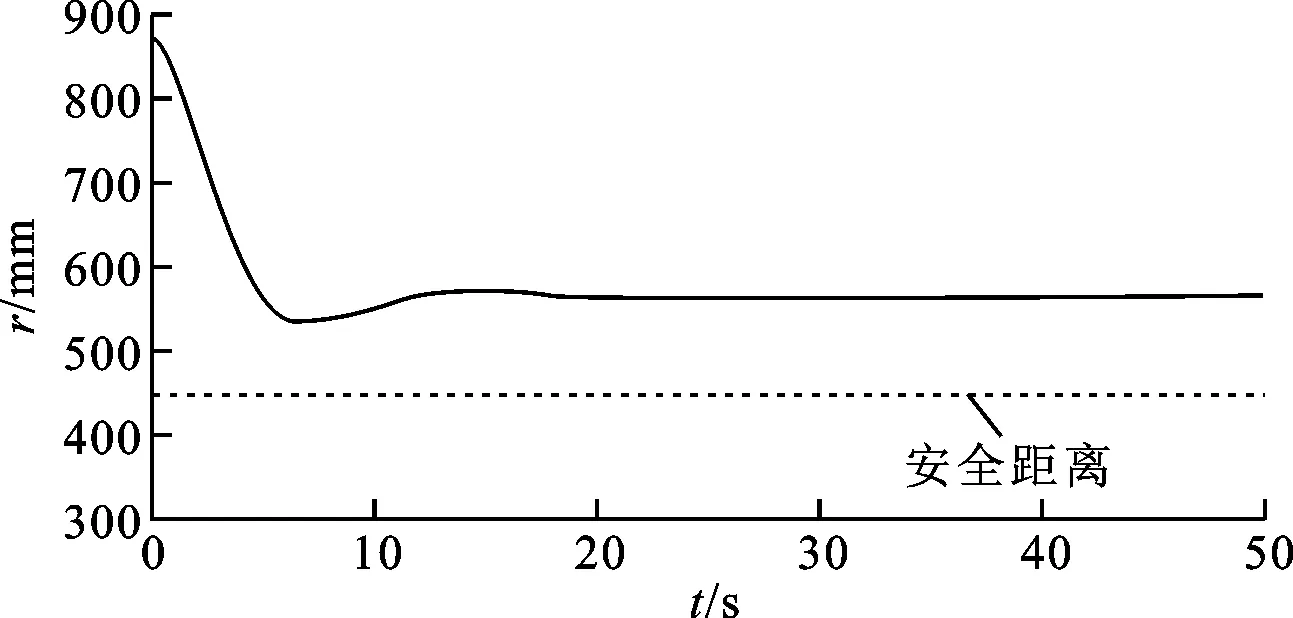
圖6 無人機編隊與障礙物相對橫側向距離的變化曲線

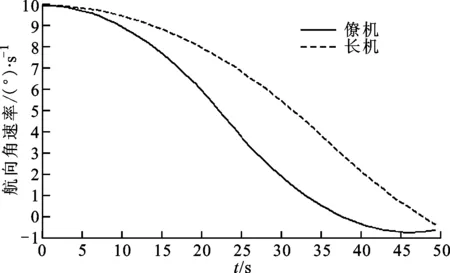
圖7 無人機避障航向角速率的變化曲線

由圖6和圖7可知,運動的障礙物以等速定高飛行,它與無人機編隊的安全距離為45 m,在剛開始的5 s,無人機編隊靠近障礙物,此時無人機編隊識別障礙物,啟動避障算法,5～15 s進行規避機動,15 s之后無人機編隊與障礙物在橫側向保持相對距離為8 m。在此期間,長機的航向角逐漸減小,為確保避障安全且保持隊形,兩僚機的航向角也隨之減小,成功避障后,按照既定的軌跡飛行。

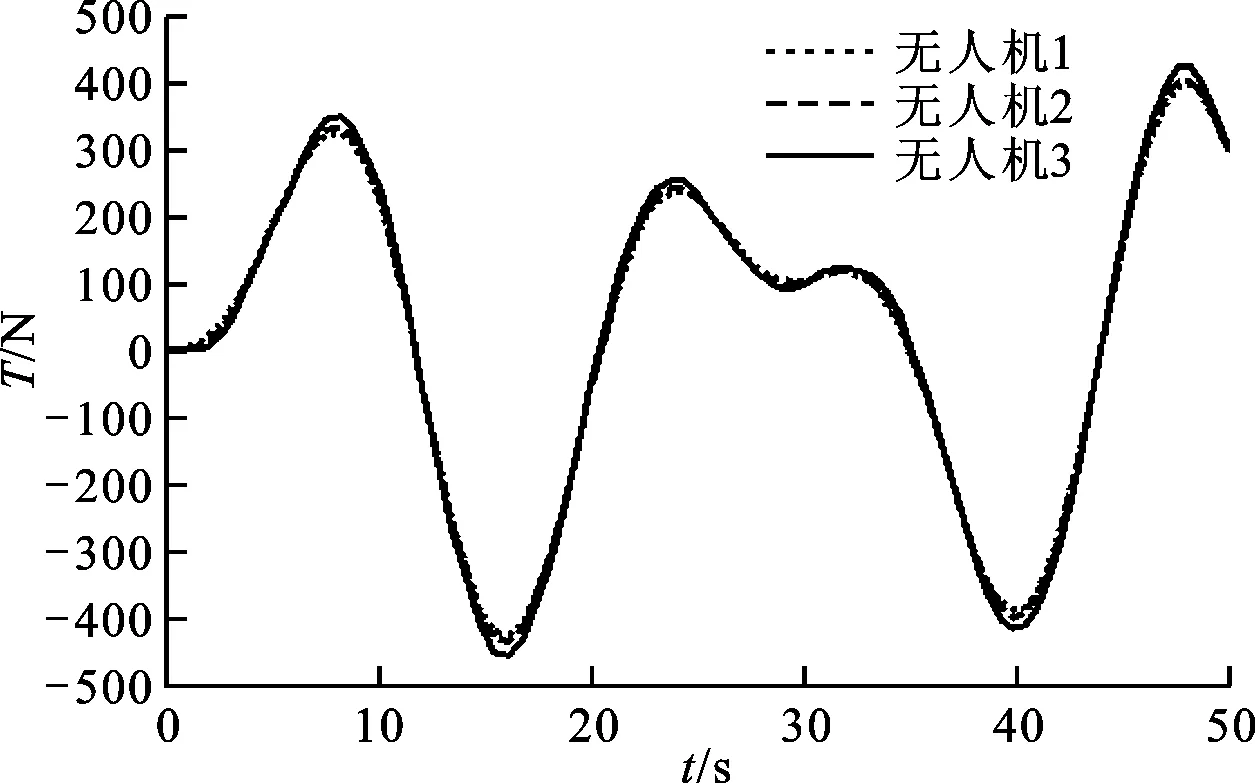
(a)未加入避障算法時間響應

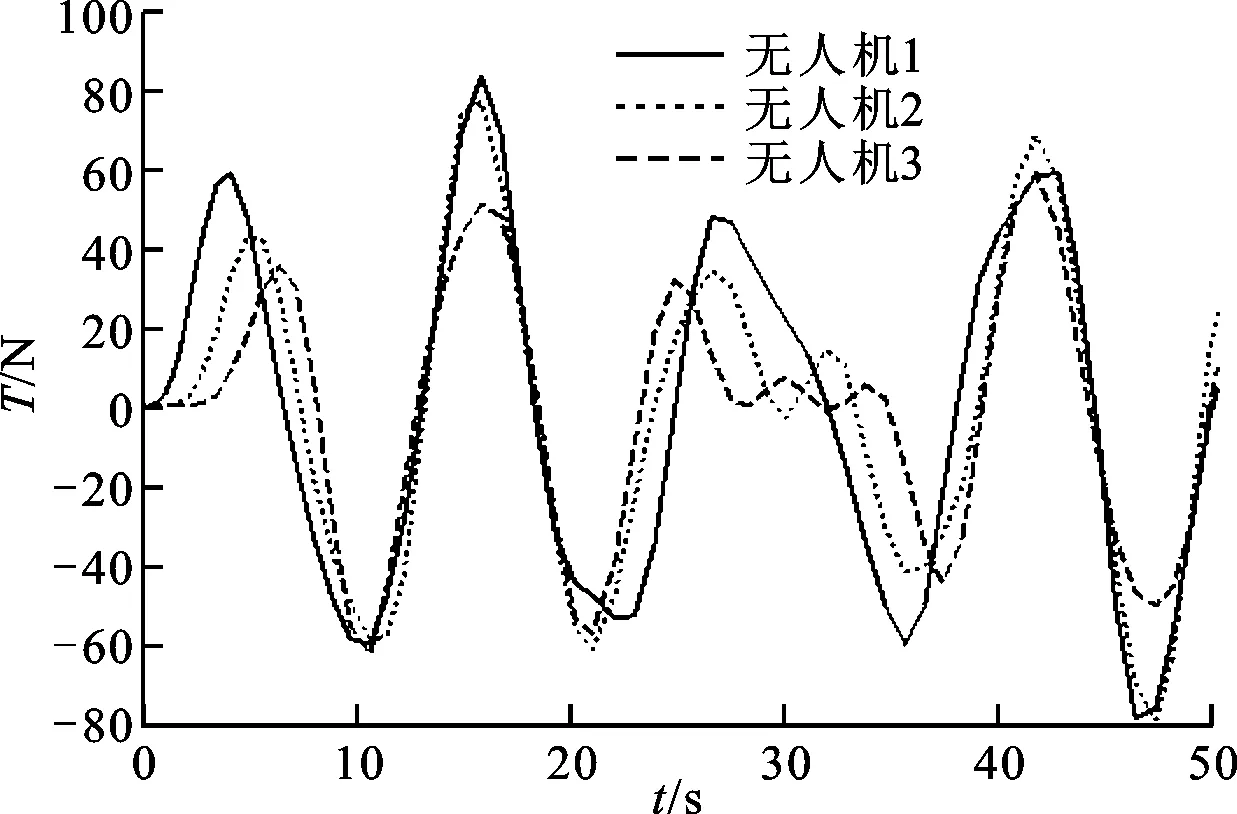
(b)加入避障算法時間響應圖8 無人機編隊中每架無人機的推力變化曲線

由圖8a可知,為了保證無人機編隊飛行信息一致性,3架無人機構成正三角形編隊系統,每架無人機保持相同的推力指令協同編隊飛行;由圖8b可知,加入避障控制算法后,3條曲線相互之間有偏差,且峰值有所不同。這是由于無人機編隊遇到障礙物時以長機飛行軌跡為預定路徑,兩僚機追蹤長機,此時長機必須采取橫側向偏轉和垂直方向升降進行避障機動,而僚機根據指令做相應的規避機動,因此3架無人機的推力略有差別。

5 總結與展望

本文使用圖論建立了一種線性化無人機編隊模型,提出一種三維空間內無人機編隊協同控制避障算法,在滿足建立模型和仿真假設的條件下,通過仿真實驗證明了所提算法的收斂性和有效性。該算法將三維空間復雜避障問題簡化為水平面的避障控制和垂直方向控制,在垂直方向無人機編隊中的任意兩架無人機之間的相對高度小于安全避障區域高度,采用規避機動方式避障,在水平面采用人工勢場方法避障。本文只是理論上的研究,并沒有進行實體實驗,而實體實驗涉及大量不可控因素,因此將該算法植入編隊控制器當中應用于工程實踐,是下一步主攻研究課題。