基于時(shí)序模型的顫振預(yù)測(cè)技術(shù)研究
劉立坤 張春蔚 王東森


摘要:本文主要研究了顫振邊界預(yù)測(cè)應(yīng)用技術(shù),針對(duì)湍流激勵(lì)下的結(jié)構(gòu)響應(yīng)數(shù)據(jù),采用遺忘因子最小二乘法建立時(shí)序模型,結(jié)合Jury穩(wěn)定性判據(jù)構(gòu)造不同飛行速度下的穩(wěn)定性參數(shù),通過(guò)外推得到顫振臨界速度預(yù)測(cè)結(jié)果。以仿真試驗(yàn)為例,討論了臨近邊界速度大小和響應(yīng)數(shù)據(jù)時(shí)間長(zhǎng)度等因素對(duì)預(yù)測(cè)精度的影響。最后結(jié)合顫振風(fēng)洞試驗(yàn)實(shí)測(cè)數(shù)據(jù)驗(yàn)證了該方法的合理性和工程實(shí)用性。
關(guān)鍵詞:顫振邊界預(yù)測(cè);時(shí)序模型;遺忘因子最小二乘法
中圖分類(lèi)號(hào):V217 文獻(xiàn)標(biāo)識(shí)碼:A
顫振飛行試驗(yàn)是新型或結(jié)構(gòu)有重大改變的飛行器都必須進(jìn)行的試飛項(xiàng)目之一,它使用真實(shí)飛行器在實(shí)際飛行條件下進(jìn)行試驗(yàn),具有典型的高風(fēng)險(xiǎn)、高耗費(fèi)和長(zhǎng)周期的特點(diǎn)。顫振邊界預(yù)測(cè)技術(shù)是顫振試飛中確定顫振邊界的主要手段。由于顫振飛行試驗(yàn)條件的復(fù)雜性,試驗(yàn)數(shù)據(jù)的品質(zhì)較低,顫振數(shù)學(xué)模型存在諸多不確定因素,顫振包線一般很難直接從試驗(yàn)獲得,因此如何基于亞臨界響應(yīng)測(cè)量與分析進(jìn)而完成對(duì)包線的預(yù)估十分重要[1]。
國(guó)內(nèi)在風(fēng)洞顫振試驗(yàn)中,常用的亞臨界顫振邊界預(yù)測(cè)方法主要包括阻尼外推法和穩(wěn)定性參數(shù)法,但多數(shù)都需要通過(guò)模態(tài)參數(shù)辨識(shí),獲取不同條件下結(jié)構(gòu)的固有頻率和阻尼比。阻尼外推法通過(guò)直接外推臨界參數(shù)確定顫振邊界;穩(wěn)定性參數(shù)法則由模態(tài)頻率和阻尼換算得到特征多項(xiàng)式的復(fù)數(shù)特征根,通過(guò)根和系數(shù)的關(guān)系構(gòu)建勞斯判據(jù)或Jury判據(jù)穩(wěn)定性參數(shù),然后進(jìn)行臨界參數(shù)外推確定顫振邊界。穩(wěn)定性參數(shù)法在國(guó)內(nèi)外已有廣泛的應(yīng)用,常見(jiàn)的著作和論文主要有管德院士的《氣動(dòng)彈性試驗(yàn)》[2]、宇航出版社出版的《防空導(dǎo)彈結(jié)構(gòu)與強(qiáng)度》[3]、中國(guó)空氣動(dòng)力研究與發(fā)展中心郭洪濤等編寫(xiě)的《顫振試驗(yàn)數(shù)據(jù)處理技術(shù)研究》[4]等。然而,由于存在激勵(lì)力不足、測(cè)量點(diǎn)有限、試驗(yàn)條件復(fù)雜及測(cè)試條件惡劣等問(wèn)題,顫振試驗(yàn)特別是飛行試驗(yàn)測(cè)量的試驗(yàn)數(shù)據(jù)品質(zhì)較低,數(shù)據(jù)往往具有模態(tài)密集、有效樣本短和數(shù)據(jù)信噪比低等特征,這些問(wèn)題的存在大大增加了模態(tài)參數(shù)識(shí)別的技術(shù)難度,進(jìn)而影響到顫振邊界預(yù)測(cè)結(jié)果的準(zhǔn)確性。
目前,國(guó)內(nèi)基于時(shí)序模型的顫振邊界預(yù)測(cè)方法較為少見(jiàn),本文通過(guò)直接識(shí)別時(shí)序模型多項(xiàng)式系數(shù)獲得穩(wěn)定性參數(shù),不必經(jīng)過(guò)模態(tài)參數(shù)辨識(shí),提供了一種基于時(shí)序模型的顫振邊界預(yù)測(cè)方法,以仿真試驗(yàn)為例,討論臨近顫振邊界不同速度大小和響應(yīng)數(shù)據(jù)時(shí)間長(zhǎng)度等因素對(duì)預(yù)測(cè)精度的影響。最后結(jié)合顫振風(fēng)洞試驗(yàn)實(shí)測(cè)數(shù)據(jù)驗(yàn)證了該方法的合理性和工程實(shí)用性。
1 方法介紹
1.1 遺忘因子最小二乘算法
遺忘因子最小二乘算法最初由Lennart Ljung于1999年提出[5],廣泛應(yīng)用于控制系統(tǒng)辨識(shí)領(lǐng)域,其思想是利用前一時(shí)刻的響應(yīng)對(duì)下一時(shí)刻進(jìn)行預(yù)測(cè),根據(jù)當(dāng)前的預(yù)測(cè)誤差設(shè)置適當(dāng)?shù)脑鲆嬷担瑏?lái)影響預(yù)測(cè)的趨勢(shì),經(jīng)過(guò)迭代運(yùn)算,使得最終的預(yù)測(cè)誤差達(dá)到最小,并以誤差最小時(shí)的參數(shù)作為系統(tǒng)辨識(shí)的結(jié)果。具體算法如下,假設(shè)時(shí)間序列{y(t);t=1,2,…,N}是測(cè)量到的一組響應(yīng)值,則有:式中:ε(t)是t時(shí)刻預(yù)測(cè)誤差Ψ班(t)是t時(shí)刻斜率,θ(t)是t時(shí)刻的參數(shù)估計(jì)值,y(t)是t時(shí)刻的響應(yīng)值(t)是由t-1時(shí)刻響應(yīng)得出的t時(shí)刻響應(yīng)預(yù)測(cè)值,增益K(t)為當(dāng)前預(yù)測(cè)誤差對(duì)參數(shù)估計(jì)的影響程度,λ是遺忘因子取值為1,通過(guò)不同時(shí)刻的循環(huán)迭代使得J(θ)最小,并以θ值作為系統(tǒng)辨識(shí)的結(jié)果[6~8]。
1.2 ARMA氣動(dòng)彈性系統(tǒng)辨識(shí)[9~12]
假設(shè){y(t);t=1,2…,N}為N自由度氣動(dòng)彈性系統(tǒng)經(jīng)大氣湍流激勵(lì)的響應(yīng),將其表示成自回歸滑動(dòng)平均(ARMA)模型的差分方程形式:式中:e(t)是零均值、方差桅σ2的白噪聲;變量z-1為后移算子,z-1y(t)=y(t-1),多項(xiàng)式系數(shù)A(z-1)和B(z-1)分別為:式中:n和m分別為自動(dòng)回歸(AR)和滑動(dòng)平均(MA)多項(xiàng)式階次。
由于白噪聲項(xiàng)e(t)無(wú)法測(cè)量,由過(guò)去時(shí)刻的數(shù)據(jù)y(t)得到的預(yù)測(cè)旬(t)為:
定義預(yù)測(cè)誤差為:
聯(lián)立式(8)和式(11)得:
將式(13)帶入遺傳因子最小二乘算法,經(jīng)過(guò)迭代運(yùn)算,即可得到ARMA多項(xiàng)式系數(shù)。
1.3 穩(wěn)定裕度估計(jì)
假設(shè)經(jīng)過(guò)遺忘因子算法辨識(shí)出ARMA多項(xiàng)式系數(shù),將其表示成特征多項(xiàng)式形式:
對(duì)于離散系統(tǒng)使用Jury穩(wěn)定性判據(jù)判斷系統(tǒng)的穩(wěn)定性,對(duì)于k=1,3,…,n-1,定義k階方陣Xk、Yk為:Jury判據(jù)要求:
Jury判據(jù)要求:
計(jì)算不同速度、不同模態(tài)結(jié)構(gòu)的穩(wěn)定性因子F-(n-1),n為ARMA模型階次,繪制穩(wěn)定性因子隨速度的變化曲線,并使用二次曲線擬合的方法進(jìn)行外推,就能得到穩(wěn)定性參數(shù)為零時(shí)對(duì)應(yīng)的速度值,即為顫振臨界速度值。
2 仿真數(shù)據(jù)驗(yàn)證分析
為驗(yàn)證該方法在湍流激勵(lì)情況下的有效性,以得克薩斯A&M大學(xué)航空航天工程系的俯仰一滾轉(zhuǎn)氣動(dòng)彈性風(fēng)洞模型為算例[3],主要研究了不同速度區(qū)間下的數(shù)據(jù)點(diǎn)數(shù)和響應(yīng)數(shù)據(jù)時(shí)間長(zhǎng)度對(duì)預(yù)測(cè)結(jié)果的影響。
在MATLAB中進(jìn)行數(shù)值仿真試驗(yàn),其動(dòng)力學(xué)模型見(jiàn)式(18),具體取值見(jiàn)參考文獻(xiàn)[6]。該模型為二自由度系統(tǒng),模型階次真值為4,顫振速度Vflutter為12.7m/s,對(duì)應(yīng)的速度頻率和速度阻尼曲線如圖1和圖2所示。
采用零均值高斯白噪聲模擬真實(shí)大氣湍流激勵(lì)形式進(jìn)行激勵(lì),首先分析了響應(yīng)信號(hào)時(shí)長(zhǎng)為60s、無(wú)噪聲情況下不同速度區(qū)間數(shù)據(jù)的預(yù)測(cè)結(jié)果,見(jiàn)表1。對(duì)于新型或重大改型飛機(jī),速度在0.8Vd~0.98Vd之間須經(jīng)過(guò)顫振飛行試驗(yàn)驗(yàn)證,(Vd為最大設(shè)計(jì)俯沖速度,根據(jù)CCAR25部相關(guān)條款Vd≤Vflutter/1.15),表1給出了8種典型速度區(qū)間的預(yù)測(cè)結(jié)果。其中,fz-fit為時(shí)序模型預(yù)測(cè)結(jié)果,g-fit為阻尼外推法預(yù)測(cè)結(jié)果。圖3和圖4給出了兩種情況的顫振速度預(yù)測(cè)結(jié)果圖[7-9]。
分析結(jié)果表明,低速試驗(yàn)點(diǎn)時(shí),阻尼較為分散,阻尼外推法預(yù)測(cè)誤差較大,時(shí)序模型預(yù)測(cè)結(jié)果比阻尼外推法精度高且較為保守。隨著速度逐漸接近臨界顫振速度,兩種方法預(yù)測(cè)結(jié)果趨于一致并且都較為準(zhǔn)確。
在顫振飛行試驗(yàn)中,為了得到有足夠置信度的信息,大氣湍流激勵(lì)方法常要求飛行員持續(xù)保持飛機(jī)穩(wěn)定平飛狀態(tài)一定時(shí)間,采集足夠長(zhǎng)的結(jié)構(gòu)響應(yīng)信號(hào),這大大增加了試驗(yàn)的成本和風(fēng)險(xiǎn)。選取速度區(qū)間0.8Vd~0.98Vd,針對(duì)不同時(shí)間長(zhǎng)度的響應(yīng)信號(hào)數(shù)據(jù)進(jìn)行了分析,表2給出了具體分析結(jié)果。
分析結(jié)果表明,隨著響應(yīng)信號(hào)數(shù)據(jù)樣本的減少,基于時(shí)序模型的預(yù)測(cè)方法預(yù)測(cè)精度逐漸降低。但即使是5s的短時(shí)數(shù)據(jù)樣本情況,該方法仍然具有一定的精度。
3 顫振飛行試驗(yàn)數(shù)據(jù)處理中的應(yīng)用
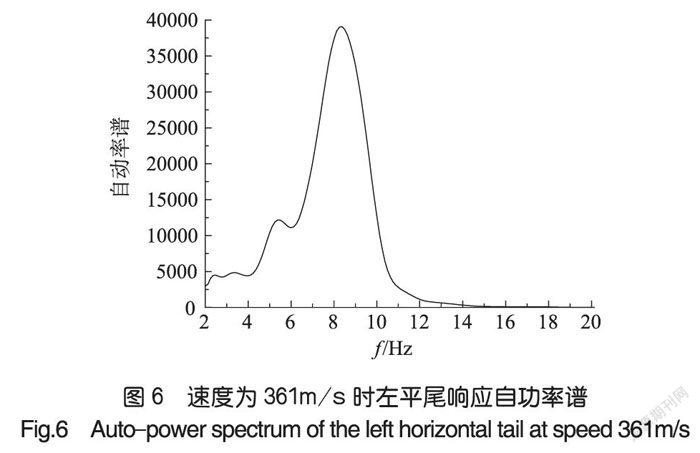
某型飛機(jī)風(fēng)洞試驗(yàn),采用大氣湍流激勵(lì),利用布置在平尾、垂尾等位置的加速度傳感器測(cè)量結(jié)構(gòu)響應(yīng)。在速度201~381m/s的部分試驗(yàn)點(diǎn)進(jìn)行試驗(yàn),圖5~圖7給出了部分速度下左平尾結(jié)構(gòu)響應(yīng)自功率譜曲線,在速度381m/s時(shí),頻域兩模態(tài)頻率歸一、響應(yīng)幅值明顯放大,速度381m/s已非常接近顫振速度。考慮到試驗(yàn)的安全性,在該速度點(diǎn)終止試驗(yàn)。分別使用基于時(shí)序模型的預(yù)測(cè)方法和阻尼外推法進(jìn)行顫振速度預(yù)測(cè)[10~12]。
圖8給出了部分試驗(yàn)點(diǎn)的顫振速度預(yù)測(cè)結(jié)果,fz為穩(wěn)定性因子值,g為結(jié)構(gòu)阻尼比,fz-fit為穩(wěn)定性因子外推擬合曲線,g-fit為阻尼外推擬合曲線。圖中,阻尼外推法顫振速度預(yù)測(cè)值約為411m/s,基于時(shí)序模型的顫振預(yù)測(cè)方法預(yù)測(cè)值約為403m/s,兩種方法預(yù)測(cè)結(jié)果一致性較好。
4 結(jié)論
采用基于時(shí)序模型的顫振邊界預(yù)測(cè)方法,對(duì)湍流激勵(lì)下的氣動(dòng)彈性模型進(jìn)行顫振邊界預(yù)測(cè),并與傳統(tǒng)阻尼外推法進(jìn)行了對(duì)比分析。仿真試驗(yàn)結(jié)果表明,基于時(shí)序模型的顫振預(yù)測(cè)方法在接近顫振臨界速度時(shí)與阻尼外推法預(yù)測(cè)結(jié)果一致,并且由于穩(wěn)定性因子隨速度成近似線性變化的關(guān)系,在低速試驗(yàn)點(diǎn)時(shí)其預(yù)測(cè)精度較阻尼外推法有一定的優(yōu)勢(shì)。
將該方法應(yīng)用于某型飛機(jī)風(fēng)洞試驗(yàn)數(shù)據(jù),對(duì)平尾進(jìn)行顫振速度預(yù)測(cè),結(jié)果表明,該方法能夠得出工程適用的顫振速度預(yù)測(cè)值。此外,與阻尼外推法相比,該方法對(duì)于湍流激勵(lì)得到的短時(shí)響應(yīng)信號(hào)也有一定的適應(yīng)能力,在實(shí)際飛行試驗(yàn)中,能夠有效保障科研試飛的安全,降低飛行試驗(yàn)的風(fēng)險(xiǎn),具有一定的工程使用價(jià)值。
參考文獻(xiàn)
[1]張偉偉,鐘華壽,肖華,等.顫振飛行試驗(yàn)的邊界預(yù)測(cè)方法回顧與展望[J].航空學(xué)報(bào),2015,36(5):1367-1384.
[2]管德.氣動(dòng)彈性試驗(yàn)[M].北京:北京航空航天大學(xué)出版社,1986.
[3]許椿蔭.防空導(dǎo)彈結(jié)構(gòu)與強(qiáng)度[M].北京:中國(guó)宇航出版社,2006.
[4]郭洪濤.顫振試驗(yàn)數(shù)據(jù)處理技術(shù)研究[D].綿陽(yáng):中國(guó)空氣動(dòng)力研究與發(fā)展中心,2005.
[5]Jung L.System identification:Theory for the user[M].Beijing:Tsinghua University Press,2002.
[6]Baldelli D H,Zeng J,Lind R,et al.Flutter-prediction toolfor flight-test-based aeroelastic parameter-varying models[J].Journal of Guidance Control&Dynamics,2009,32(1):158-171.
[7]Matsuzaki Y Flutter boundary prediction based on Jury,s stabil-ity criterion:a review[C]//Aiaa/asme/asce/ahs/asc Structures,Structural Dynamics and Materials Conference,2011.
[8]Matsuzaki Y.Flutter boundary prediction of digitalized smartmultimode systems using steady-state responses[C]//Aiaa/asme/asce/ahs/asc Structures,Structural Dynamics and MaterialsConference,2006.
[9]Torii H,Matsuzaki Y Flutter margin evaluation for three-modediscrete-time systems[J].Journal ofAircraft,2013,38(1):42-47.
[10]AlAA.Flutter prediction of multimode systems from their tur-bulent responses by Jurys criterion[C]//Aiaa/asme/asce/ahs/asc Structures,Structural Dynamics and Materials Conference,2013.
[11]Matsuzakir Y Flutter boundary prediction of an adaptive smartwing during process of adaptation[R].Proc Spie,2005:5764.
[12]Matsuzaki Y,Torii H.Flutter boundary prediction of a smartwing in process of structural adaptation[C]//Aiaa/asme/asce/ahs/asc Structures,Structural Dynamics and Materials Conference,2007.

