基于槳距控制的電力系統頻率響應特性

馮家銓， 陳堂賢， 唐紅艷， 呂翔生

(三峽大學 電氣與新能源學院，湖北 宜昌 443002)

0 引言

隨著風電滲透率不斷提高，電力系統的頻率會受到越來越嚴峻挑戰，同時還會對電網的穩定性造成不良影響[1～3]。目前，針對風電場接入電網使系統頻率跌落的情況，國內外最新發布的一些電網導則明確提出并網風電場需要和常規發電廠一樣具有參與系統一次調頻的能力[4]。其中，文獻[5～7]提出當系統頻率降低時，通過調節槳距角或通過調整功率來增加有功輸出參與頻率調整。同時，GE風機廠商于2003年便提供了支持該項控制技術的風電機組，而加拿大魁北克地區通過風電場配置的PMU實測數據，驗證了一次調頻輔助控制在風電場和電網運行中的應用效果[8，9]。

面對一次調頻輔助控制技術逐步推廣應用的發展趨勢，如何建立含該控制技術的電網頻率特性分析計算模型已成為亟需開展的研究新課題。傳統的電力系統頻率響應分析計算模型主要包括3種：電網全時域仿真模型、平均系統頻率模型(Average System Frequency, ASF)和系統頻率響應模型(SFR)。ASF模型和SFR模型雖發展較為成熟，但僅考慮同步發電機頻率響應作用，均未計及風電頻率控制的耦合作用，已經不能適應當前風電滲透較高的電網頻率特性研究[10，11]。對此，文獻[12]計及風電一次調頻響應，提出了改進ASF模型。但是該模型采用風機的固有慣性時間常數表示慣性響應作用效果并不準確[13]，而且其一次調頻響應采用靜態模型描述，僅能反映穩態頻率偏差大小。文獻[14]將電網最低頻率跌落點和最大頻率變化率作為頻率動態響應邊界條件，提出了一種電網最大風電滲透率估計方法，但該方法并未考慮風電一次調頻作用效果。

對此，針對額定風速以上運行條件，本文采用傳遞函數模型定量表征風電場一次調頻響應，結合再熱式火電機組和水電機組的原動機—調速器模型，并針對含多個風電場/火電機組/水電機組的電力系統，基于加權等值法對各類型機組模型聚合，最終提出了含風電場槳距控制一次調頻響應及水電/火電等值機組機電暫態行為的改進SFR解析計算等值模型。根據改進的SFR模型討論了不同滲透率的風電接入對電力系統頻率響應特性的影響。考慮風電一次調頻響應作用的前提下，本文提出了一種基于槳距控制的風電有功—頻率耦合的電力系統頻率特性方法。在不考慮一次調頻響應作用的前提下，證明了風電滲透率提高時，系統一次調頻能力下降導致了系統頻率特性顯著惡化的結論。

1 改進SFR頻率響應等值模型

在含風電電力系統中，采用HΣ來表征含風電的電力系統等效慣性響應。同時，對風電機組施加基于槳距控制的一次調頻輔助控制策略，采用傳遞函數hmWF(s)來定量表征風電場的一次調頻響應作用。此外，還包括了汽輪機—調速器等值模型hmT(s)和水輪機—調速器等值模型hmH(s)的調節作用。因此，本文在傳統SFR等值模型[13，14]基礎上，并計及HΣ和hmWF(s)的作用，建立了如圖1所示的改進SFR模型。

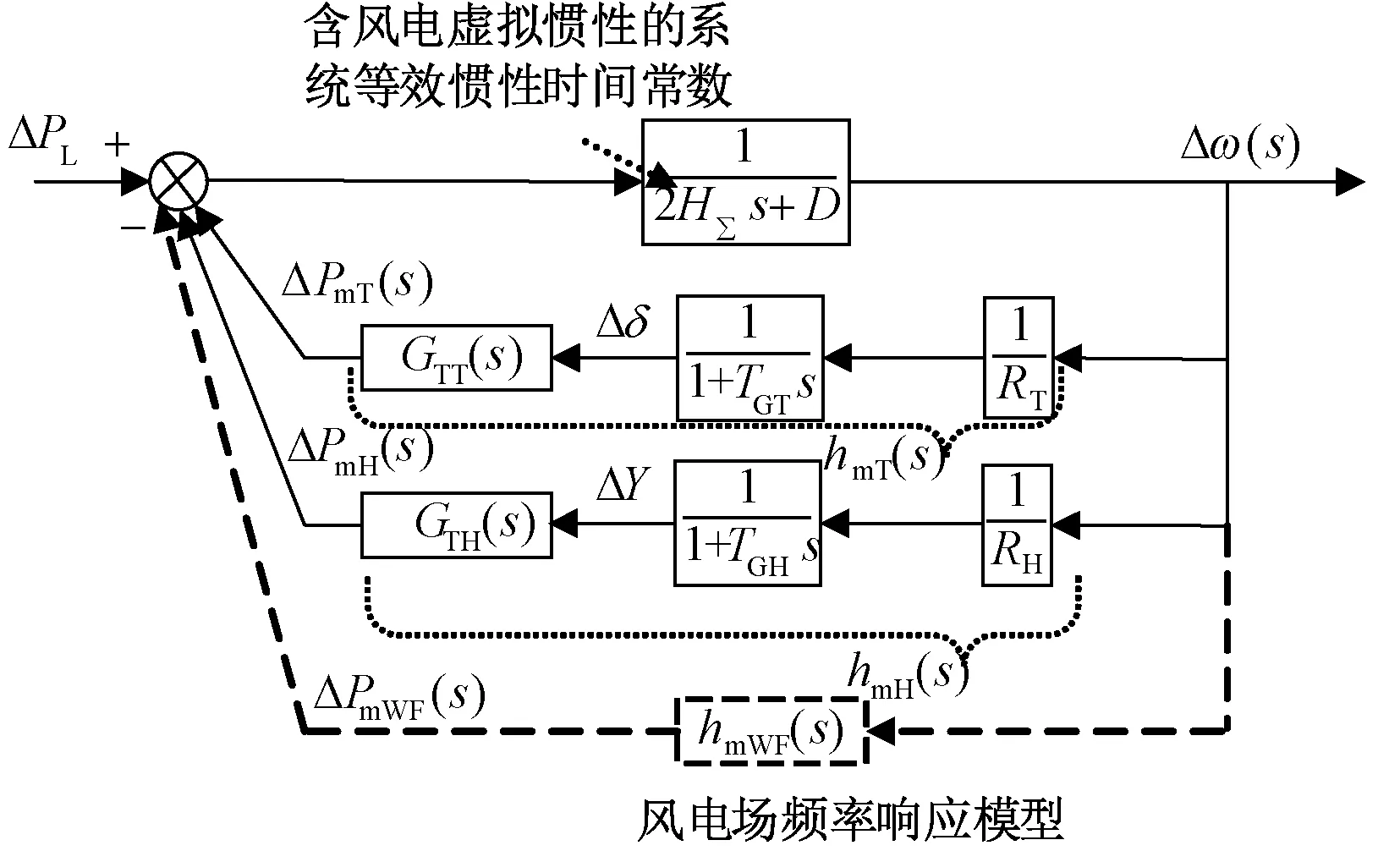
圖1 改進型SFR頻率響應模型

圖2模型中，當系統頻率處于穩態時，功率控制環單獨產生初始槳距角參考β0，并有β0=βref>0(不參與一次調頻時β0=βref=0)。當系統頻率發生擾動時，槳距一次調頻控制器產生附加槳距角Δβ和功率控制環產生的初始槳距角參考值β0一起構成總槳距角參考值βref，經伺服執行機構改變槳距角β，并最終改變輸出機械轉矩和機械功率Pm，實現了槳距一次調頻響應。

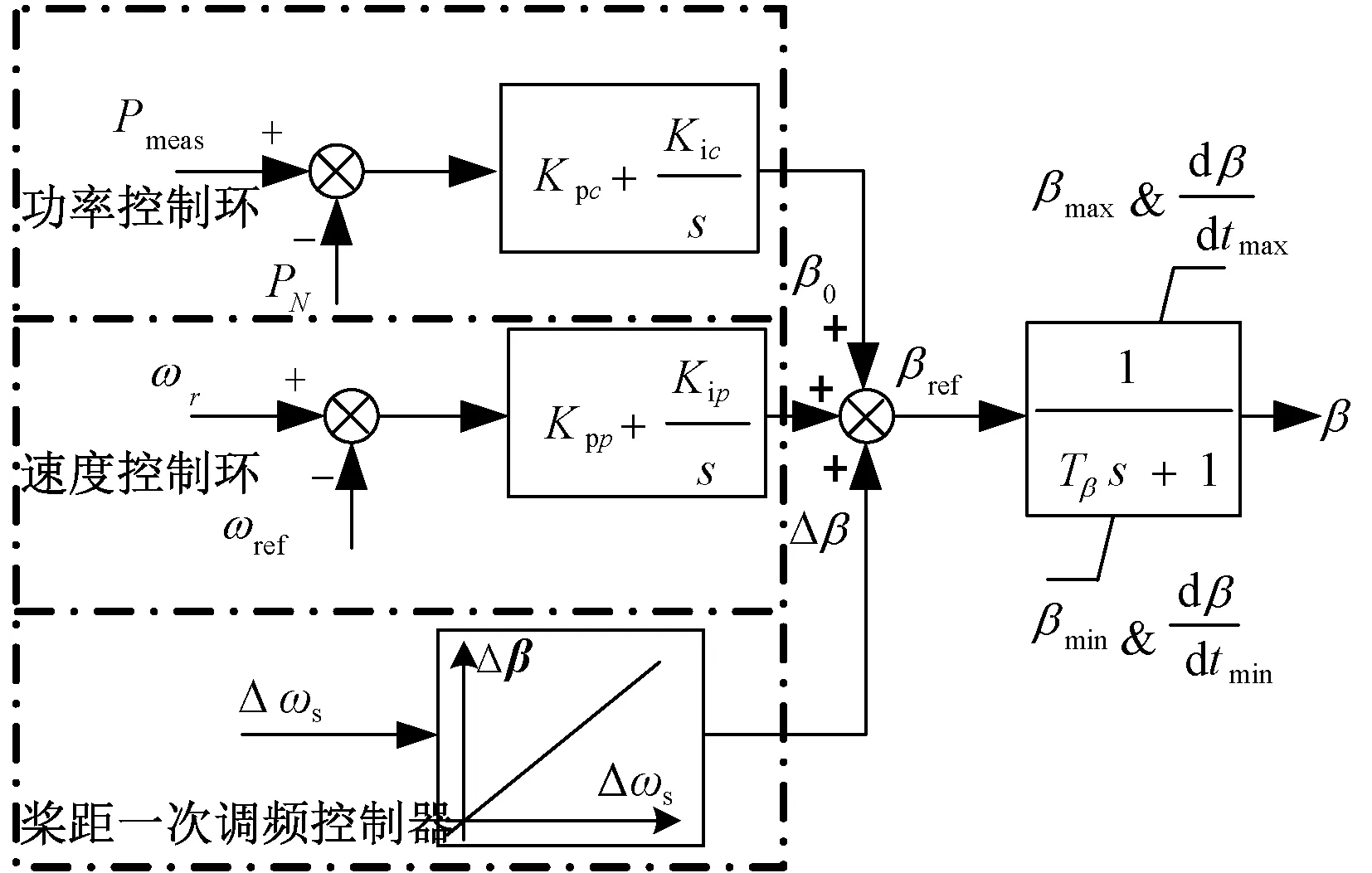
圖2 槳距一次調頻控制策略結構圖

以下部分首先分別求解圖1中hmWF(s)，HΣ，hmT(s)和hmH(s)，再建立改進SFR模型。

2 電力系統等值模型及參數計算

2.1 等值方法

在圖1中，將電力系統中所有機組等值為3臺火電機組、水電機組和風電機組。而本文采用文獻[20，21]中提出的基于加權的動態等值參數聚合方法，分別對火電機組群、水電機組群和風電機組群進行參數等值計算。設通過同調方法識別得知某個機群(火電、水電或風電)包括N臺機組集合G={1,2…j…N}，并假設同群機組轉子角速度相同為ω，則等值機組的參數為：

?j∈G

(1)

式中：KG表示等值機參數；下標j，G分別為機群中第j臺機組等值。

2.2 風電場一次調頻響應聚合模型

當采用槳距一次調頻輔助控制策略時，由文獻[17]中的小信號求解方法和式(1)的等值加權方法，可得多臺風機的動態頻率響應模型傳遞函數hmWF(s)，可表示為：

(2)

式中：Kdβ，Tβ，Cβ，Kpc/Kic分別為槳距控制增益，槳距伺服時間常數，槳距增量系數，槳距功率環PI參數。k0，w0，w1，w2分別為傳遞函數hmWF(s)的各項等值參數。

2.3 火/水電機組等值模型

根據文獻[22]中的汽輪機—調速器模型，同時，利用式(1)的加權等值法，將系統中火電機組等值為一臺機，等值汽輪機—調速器的傳遞函數模型可表示為：

(3)

式中：FHPG為高壓渦輪級功率占比；TRHG為再熱器時間常數；RTG為汽輪機調差系數。

當同步機組為水電機組時，根據文獻[22]中的水輪機—調速器模型和利用式(1)的加權等值法，將系統中水電機組等值為一臺機，等值水輪機—調速器的傳遞函數模型可表示為：

(4)

式中：RHG，TwG分別表示為水輪機調差系數、水錘效應系數的等值聚合參數。

2.4 計及風電的系統等效慣性時間常數

采用槳距控制的一次調頻輔助控制策略時，系統不進行虛擬慣性響應，這是由于風機轉速被鉗制在額定轉速。計算不同風電滲透率下系統等效慣性時間常數HΣ可表示為：

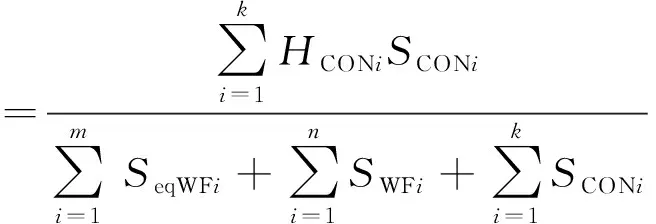
(5)

式中：HCONi為常規電場慣性時間常數；SCONi為額定容量；SeqWFi為不含虛擬慣性控制的風電場慣性的額定容量；SWFi為含虛擬慣性控制的風電場的額定容量。

3 風電槳距控制一次調頻響應等效模型求解

對圖1改進SFR模型，實際上描述的是以系統功率缺額ΔPL(s)為輸入，系統頻率偏差Δωs(s)為輸出，系統負荷阻尼綜合模型為開環傳遞函數G(s)，并以hmT(s)、hmH(s)和hmWF(s)為反饋傳遞函數h(s)的閉環控制系統。因此，當采用槳距一次調頻輔助控制策略時，可將圖1化簡為如圖3所示的傳遞函數框圖。

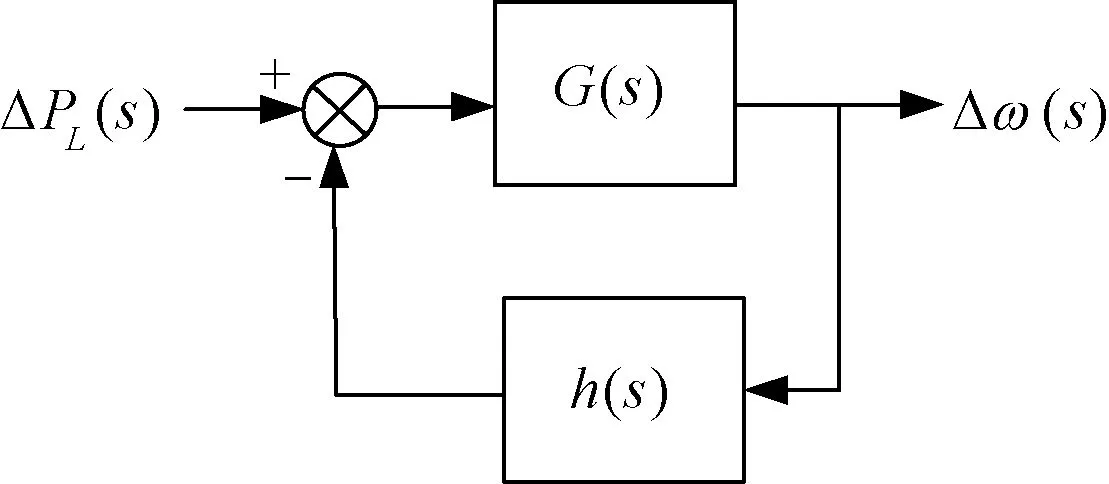
圖3 基于風電槳距一次調頻響應等效簡化傳遞函數框圖

當采用槳距一次調頻輔助控制策略時，由式(5)可得，向開環傳遞函數為：

(6)

式中：D為負荷阻尼系數。

反饋傳遞函數h(s)為:

h(s)=hmT(s)+hmH(s)+hmWF(s)=

(7)

對應的閉環傳遞函數為：

(8)

Φ(s)在負荷突增階躍響應ΔPL(s)/s下的Δωs(s)響應可表示為：

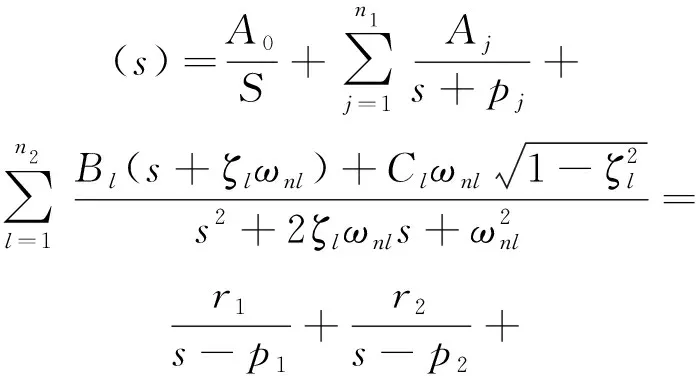
(9)

式中：A0是Δωs(s)在s=0處的留數；n1是實數根個數；Aj是Δωs(s)在實數極點s=-pj處的留數；n2是共軛復數根的對數；Bl和Cl分別為Δωs(s)在共軛復數極點處s=-(Bl±jCl)留數的實部和虛部；ζl是共軛復數根反映的二階系統阻尼系數；ωnl是共軛復數根反映的二階系統振蕩角頻率；r為部分分式展開的余數數組；p為部分分式展開的極點數組；k為常數項。由此可得到頻率偏差的時域解為：

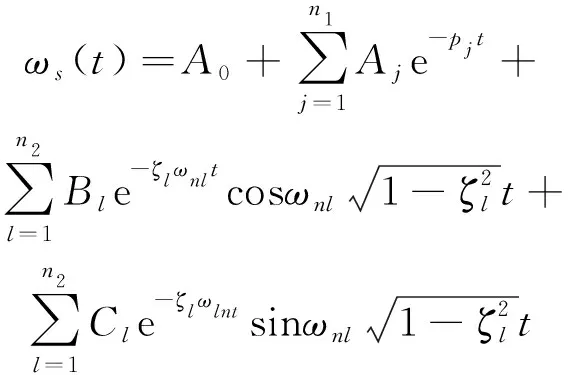
(10)

式中：Δωs(t)的各項系數A0，Aj，pj，Bl，Cl，ζl，ωnl可由式(10)部分分式展開后計算得到。

由此可得到功率缺額擾動后的系統頻率時域解為：

f(t)=f0+2πΔωs(t)f0

(11)

式中：f0為系統初始頻率，穩態時f0=fN(額定頻率)。

4 算例分析

在MATLAB/SIMULINK環境下，利用圖4的仿真系統，對圖中風電場的風電機組實施基于槳距一次調頻輔助控制策略時，驗證式(11)中系統頻率解析計算結果的精確性，證明采用圖1中改進SFR解析模型能客觀描述含風電有功/頻率控制的電力系統頻率特性和不同一次調頻增益對電力系統頻率特性的影響。具體通過比較無風電有功/頻率控制的非線性全狀態仿真模型(后稱模型1)、計及風電有功頻率控制的非線性全狀態仿真模型(后稱模型2)和改進SFR模型(后稱模型3)的f(t)動態響應曲線來進行驗證和說明，驗證改進SFR模型的精確性。其中，模型1僅考慮同步發電機簡化模型；模型2計及同步發電機(包括火/水電機組)的慣性響應和調速器—原動機非線性模型，并計及風電一次調頻響應，同時風電機組采用GE風機的非線性全階模型。

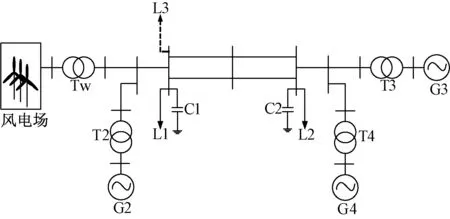
圖4 仿真系統

仿真項目包括：1)不同風電滲透率條件下，負荷突增、頻率跌落時，基于風電槳距一次調頻輔助控制的系統頻率響應；2)初始風速Vw=10 m/s，設置不同Kdβ，反映風電槳距一次調頻輔助控制的系統頻率響應。

4.1 不同滲透率下系統突增負荷時的系統頻率響應

當發生系統突增10%負荷頻率事故時，比較模型1，模型2和模型3的系統f頻率跌落曲線。圖5(a)～(c)是風電滲透率分別為10%，20%，30% 的電網條件下模型1，模型2，模型3的比較結果。各條件和情況下均設置風速Vw=15 m/s。

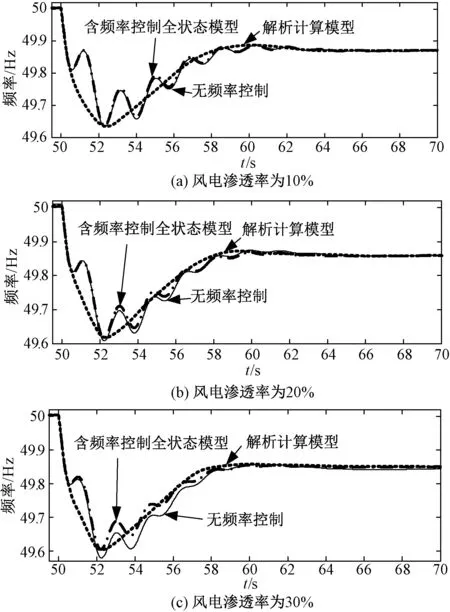
圖5 突增負荷時不同滲透率下系統頻率響應

由于不同的滲透率下有不同的頻率響應，在仿真過程中可能超過系統承受的最大穿透功率極限，所以出現振蕩情況。由圖5可知，采用模型1時，隨著風電滲透率增加，頻率跌最低點降低(49.632→49.608→49.579，Hz)，頻率最低點發生時刻越早(52.313→52.247→52.237，s)，反映出電網因無采取風電槳距一次調頻輔助控制而導致頻率特性惡化現象；采用模型2時，隨著風電滲透率增加，頻率跌落最低點升高(49.635→49.616→49.605，Hz)，頻率最低點發生時刻越晚(52.306→52.220→52.212，s)，表現出采取風電槳距一次調頻輔助控制對頻率特性的改善作用。另一方面，采用模型3時，在系統頻率跌落、上升最低點及穩態精度指標上以及動態響應上均與模型2更接近，優于模型1。

4.2 不同Kdβ下系統突增負荷時的系統頻率響應

建立圖4的電網仿真算例，圖6顯示了在Kdβ為0、1倍、2倍下的系統頻率曲線，由于Kdβ增益倍數不同，系統的滲透率是不同的，所以無法開始就設定系統的滲透率。因為仿真是在穿透功率極限條件下去驗證的，所以頻率偏差是未超過振蕩邊界值。將不同Kdβ的頻率響應指標比較值列入表1中。

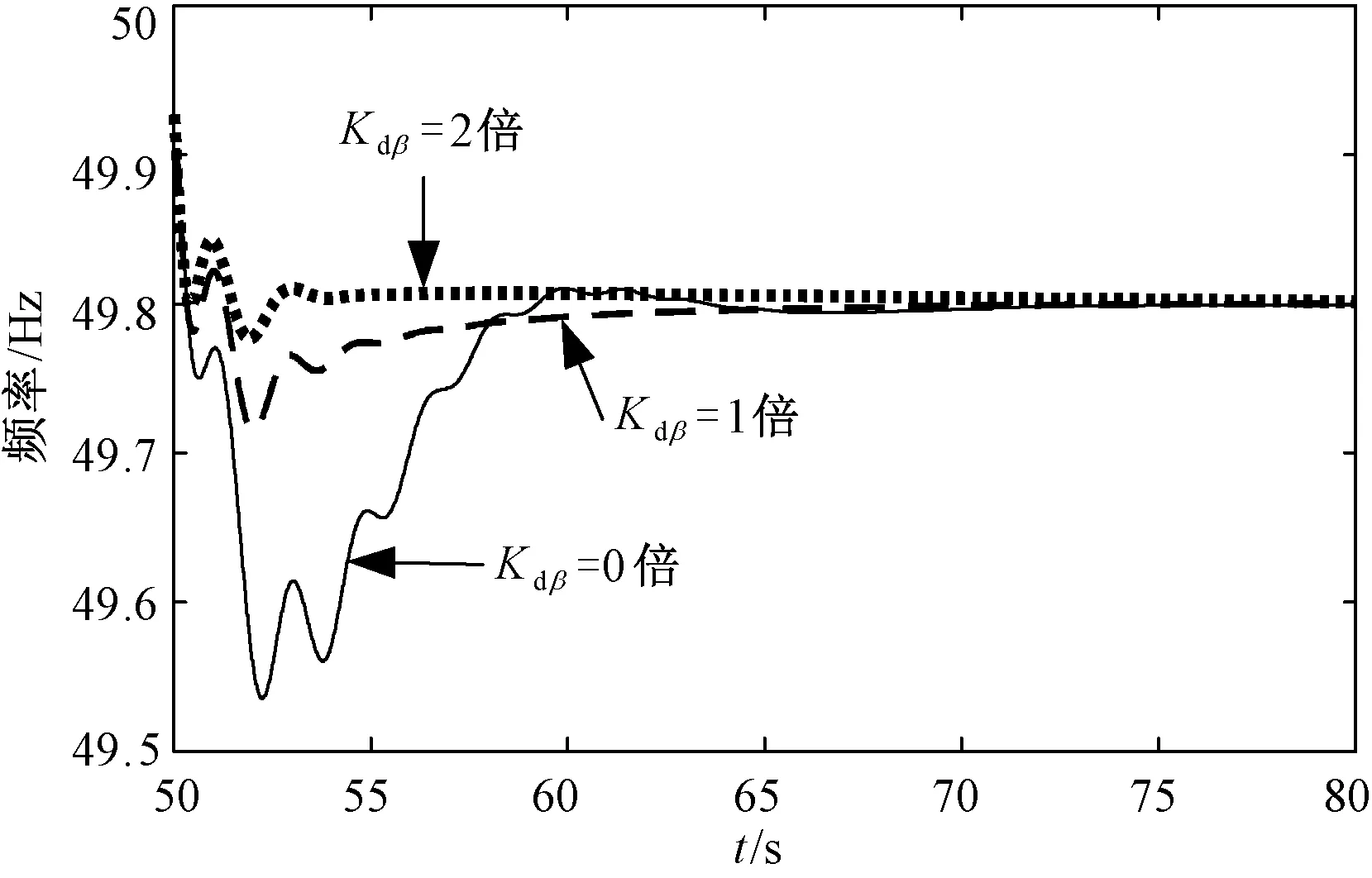
圖6 突增負荷時不同Kdβ下系統頻率響應

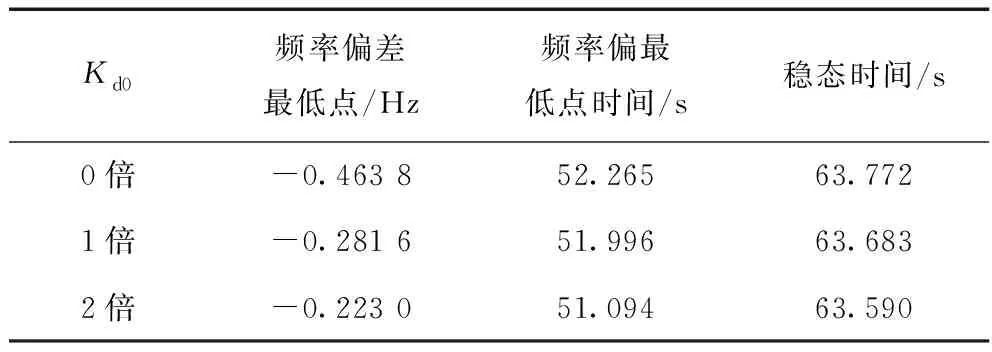
Kd0頻率偏差最低點/Hz頻率偏最低點時間/s穩態時間/s0倍-0.463 852.26563.7721倍-0.281 651.99663.6832倍-0.223 051.09463.590

表1是對應圖6的各項頻率指標統計，更加細致地反映了圖4的仿真效果。根據統計指標，采用模型3，隨著一次調頻槳距控制增益Kdβ的增加，頻率跌最低點降低，頻率最低點發生時刻越早，達到穩態時間越早，反映出了風電一次調頻對電力系統頻率的改善作用。并且隨著Kdβ增加，系統頻率響應越穩定。Kdβ增益倍數從0到2，體現控制增益從無到有，槳距控制對系統頻率的改善。

5 結論

本文針對經典SFR模型不能客觀描述含風電有功—頻率耦合電力系統的頻率特性問題，基于槳距控制的風電場一次調頻輔助控制方法，建立了改進SFR模型，主要得出結論：

(1)對建立的SFR等值模型，采用加權動態等值參數聚合法，計算了模型主要等值參數，包括不同風電滲透率下的系統等效慣性時間常數、風電場一次調頻響應等效模型參數、水電、火電機組等值模型各項等值參數；推導了含風電、火電、水電3機等值模型的系統頻率偏差頻域計算表達式。

(2)當風電滲透率越高、施加槳距一次調頻輔助控制時，模型2和模型1二者的頻率響應吻合度較差，而采用改進型的SFR模型(模型3)時，在系統頻率跌落、上升最低點及穩態精度指標上以及動態響應上均與模型2更接近，優于模型1，且隨著風電滲透率增加，改進SFR模型的頻率響應動態性能越好，越能體現采用該模型分析計算頻率特性的優越性。