基于直線加權平均的平均值法、逐差法和最小二乘法的等效假設研究

魏同利 郝惠娟 馬天鵬

(1北方民族大學電氣信息工程學院； 2寧夏大學預科教育學院，寧夏 銀川 750021)

算術平均值法、逐差法和最小二乘法是常用的3種處理等間距線性數據的方法。但是由于對這3種方法的前提、假設和使用條件的介紹和討論相對較少，在實驗教學和工程應用中出現了一些混亂，誤差處理中張冠李戴的現象并不少見。一些作者已注意到該現狀，就相關問題寫了一系列文章[1-7]。比較具有代表性的，如高永祥[5]認為“普通最小二乘法與加權最小二乘法(逐差法)的前提條件和基本假定是不相同的，不能在相同模型下比較普通最小二乘法和逐差法的優劣,否則,方法和模型會產生矛盾,得出錯誤結論”，給出不能否定也不能濫用逐差法的論斷；呂大韻提出“就其本質而言，逐差法主要是為了減小系統誤差的影響”[6]。

現行的研究相對局限在對方法本身“好或不好”的討論上，而對方法的基本假設及其所處理的“對象(數據)”缺乏系統研究。我們認為每種方法都有其假設的條件,方法是否合用，在于該方法的假設和具體數據之間的貼近程度。數據越貼近所用方法的假設，所得到的結果就越好，其對應的標準誤差越小；反之，結果就較差，其對應的標準誤差也較大。為了澄清該問題，我們以任意兩點所確定的直線為研究對象，針對等間距線性數據，對算術平均值法、逐差法和最小二乘法的基本假設進行了研究，通過確定每條直線在不同處理方法中的權重，對3種方法各提出一種等效假設。由此假設出發，建議了3種數據類型的處理方法: 在標準誤差對最小間隔相等的數據類型中，經算術平均值法計算的斜率，標準誤差最小；在標準誤差對每一點相等的數據類型中，通過最小二乘法計算的斜率，標準誤差最小；最后在不等精度的假設下(相當于一種加權平均值法),定量給出了逐差法最優的標準誤差分布，測量數據的標準誤差由兩端向中間區域以1/2次方的速率衰減時，經逐差法計算所得的斜率，標準誤差最小。

1 3種線性處理方法的等效假設

設線性數據由2n個等間距的測量點組成，分別為(x1,y1),…,(xi,yi),…(x2n,y2n)。設相鄰兩點滿足Δx1=…=Δxi=…=Δx2n-1=Δx，其中Δxi=xi+1-xi。將相鄰兩點構成的區間稱為一個基本區間，其y值之差可分別表示為Δy1,…,Δyi,…,Δy2n-1，有：Δyi=yi+1-yi。

1.1 算術平均值法的等效假設

算術平均值法可看作任意兩點所確定的直線斜率的加權運算。其加權方式可由以下假設確定:

① 最佳直線的斜率由所有基本區間的斜率按照其權重相加；

② 任意基本區間等權。

(1)

其中,bm表示該假設下等間距線性數據的最佳斜率,與平均值法的結果是一致的。

1.2 逐差法的等效假設

逐差法同樣可以看作任意兩點所確定的直線斜率的加權運算。其加權方式可由以下假設確定:

① 最佳直線的斜率由所有可能的包含n個基本區間的直線斜率按照其權重相加；

② 任意包含n個基本區間的兩點確定的直線等權。

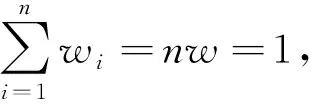
(2)

其中，bz表示該假設下等間距線性數據的最佳斜率，此假設所得到的斜率和逐差法的處理結果是一致的。可求得每一基本區間的權重為

(3)

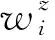
1.3 最小二乘法的等效假設

最小二乘法也可以看作直線的加權運算。其加權方式可由以下假設確定:

① 最佳斜率由所有可能直線的斜率按照其權重相加；

② 直線權重與確定它的兩點之間的基本區間個數的平方成正比。

此假設下，由指標為i和j的兩點確定的直線的權重可以表示為

Ci,j=(j-i)2w

(4)

其中,w為基本區間即相鄰兩點所確定直線的權重。在此假設下，等間距線性數據的斜率可計算如下

(5)

按照最小二乘法的計算規則，其斜率可推導如下：

(6)

該假設的基本區間權重系數和最小二乘法計算的結果中都包含有n2-(n-i)2項，由于其他參量與指標i無關，可知此假設是正確的。由式(6)可得任一基本區間的權重

(7)

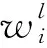
2 最佳斜率的標準誤差

2.1 基本區間等權的數據類型

在基本區間的誤差滿足正態分布且標準誤差都相等時，每一基本區間的標準誤差為

σ(Δy1)=σ(Δy2)=…=σ(Δyn)=σ

(8)

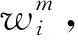
的標準誤差平方為

(9)

算術平均值法最佳斜率的標準偏差為

(10)

依據式(3)和式(7)，可求得該假設下，逐差法和最小二乘法所求得的最佳斜率的標準誤差

(11)

比較式(10)和式(11)，可以看出算術平均值法的標準誤差最小。

2.2 點等權的數據類型

在每一點的誤差滿足正態分布且其標準誤差相等的假設下，取每一點的標準誤差為

σ(y1)=σ(y2)=…=σ(yn)=σ

(12)

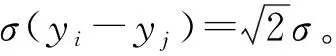
(13)

(14)

應滿足最小值條件。任意兩條直線的權重滿足以下條件

(15)

(16)

此權重系數和最小二乘法的基本假設完全相符：任兩點確定的直線的權重與其包含的基本區間的個數的平方成正比。所以在點等權的數據類型中，最小二乘法所得的斜率的標準誤差最小，其最佳斜率的標準誤差為[7]

(17)

依據式(1)和式(2)，可求得算術平均值法和逐差法的最佳斜率的標準誤差

(18)

可知在點等權的數據類型中，最小二乘法和逐差法最佳斜率的標準誤差都與n3/2成反比，而算術平均值法最佳斜率的標準誤差與n成反比，故在這種假設下最小二乘法和逐差法遠優于算術平均值法。

2.3 逐差法最優的數據類型

我們依據式(1)、式(3)和式(7)繪制了n=16時，3種方法所求最佳斜率的基本區間權重的分布圖(圖1)。算術平均值法對應基本區間的平權運算；逐差法的權重在中間n指標區域最大，起始和末尾區域的權重最小；最小二乘法在起始、中間和末尾區域的權重介于算術平均值法和逐差法之間。即算術平均值法、逐差法和最小二乘法都可以看作對基本區間的加權運算。

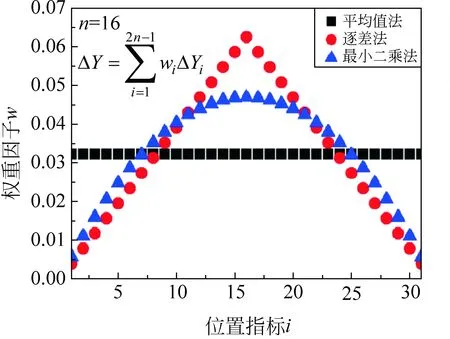
圖1 權重因子與位置的關系

由2.1節和2.2節的討論，在關于斜率的計算中,算術平均值法和最小二乘法都有與其對應的等精度數據類型，分別以算術平均值法和最小二乘法斜率的標準誤差最小。但在實際的問題中，等精度假設有時是不能成立的。逐差法的數據類型恰是這樣一種不等精度的數據類型。通過式(3)中的權重因子的比較，我們以不同位置基本區間的標準誤差為研究對象，給出其標準誤差的分布。其論證過程如下：逐差法作為該假設下最優的方法，每一基本區間的權重因子應使得Δy的標準誤差最小，即:Δyz=w1Δy1+…+wnΔyn的標準誤差最小，其標準誤差的平方可以表達為

(19)

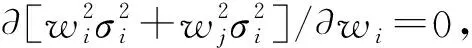
(20)

(21)

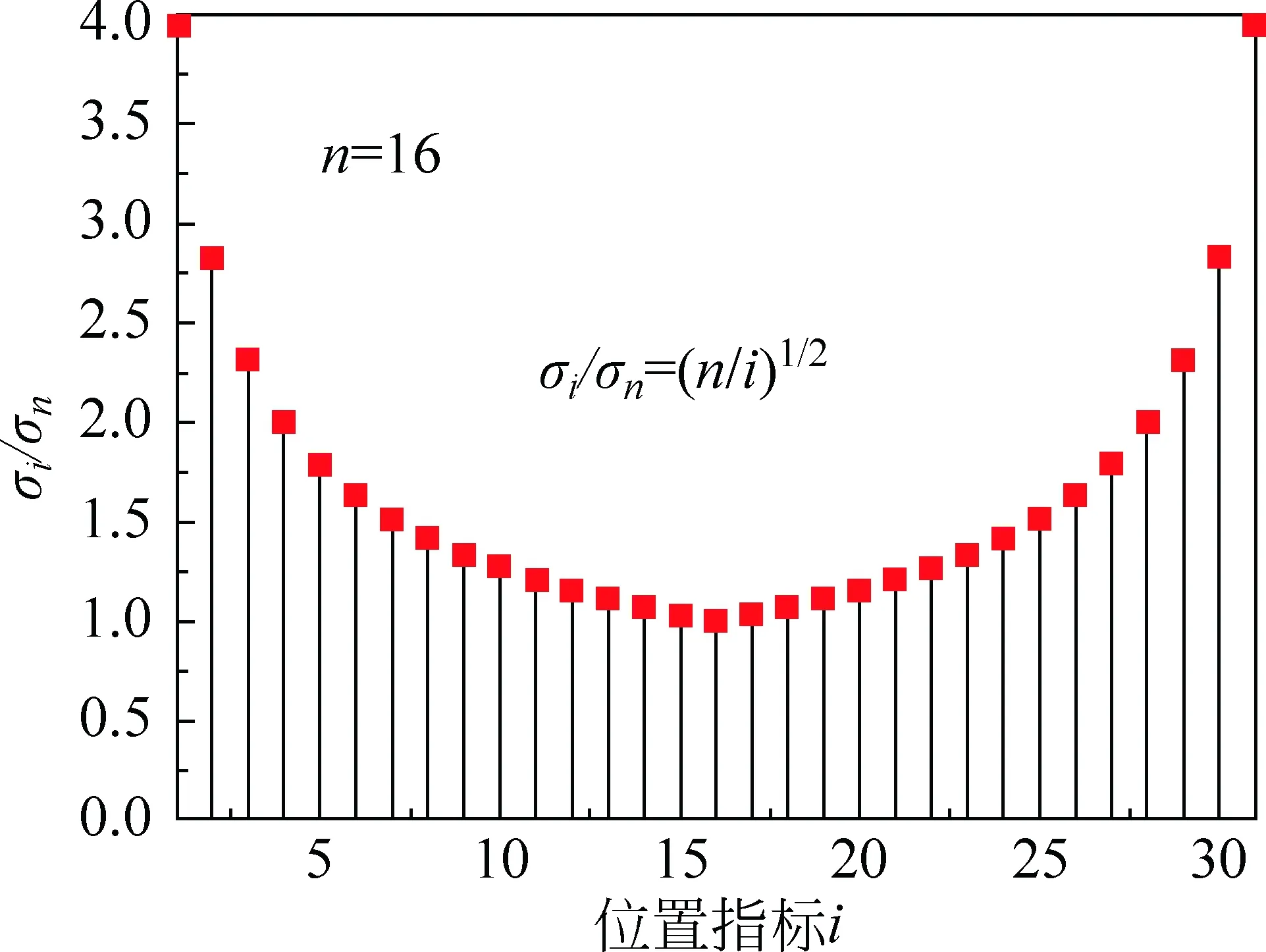
圖2 逐差法的標準誤差分布

最佳斜率的標準誤差為

(22)

3 結論

本文通過直線加權的方式系統考察了處理等間距線性數據的3種方法：算術平均值法、逐差法和最小二乘法。針對3種處理方法各提出一種較為直觀的等效假設：算術平均值法只考慮相鄰點所確定的直線，并等權地處理它們；逐差法考慮包含n個基本區間的兩點所確定的直線，等權的求其平均；最小二乘法則考慮了所有可能直線的影響，其權重與兩點之間的距離的平方成正比。

提出以算術平均值法、逐差法和最小二乘法為最優方法的3種數據處理類型：在標準誤差對最小間隔等權的數據類型中，經算術平均值法計算的斜率，標準誤差最小；在點等權的數據類型中，經最小二乘法計算的斜率，標準誤差最小；在不等精度的假設下,定量給出了逐差法最優的數據類型：測量數據的標準誤差由兩端向中間區域以1/2次方的速率衰減。對于這種兩端區域精確度低，中間區域精確度高的線性數據，選用逐差法是較優。在具體的測量中，必須仔細分析誤差的性質和來源，以確定線性數據的種類，選用合適的處理方法。

■