裝甲裝備機(jī)動搶修路線決策方法

王少華,董原生,呂會強(qiáng),劉宏祥,彭正軍

(1.裝甲兵學(xué)院 a裝備保障與再制造系； b.科研學(xué)術(shù)處， 北京 100072；2.中國人民解放軍77626部隊(duì)， 拉薩 850000)

在信息化戰(zhàn)爭中，武器裝備的威力和命中精度將大大提高，作為陸軍主戰(zhàn)力量，裝甲裝備的損傷機(jī)率將隨之提高。作為部隊(duì)補(bǔ)充和恢復(fù)戰(zhàn)斗力的主要手段，戰(zhàn)場搶修能否成功組織實(shí)施將極大程度地影響成敗。戰(zhàn)場搶修力量前出到陣地現(xiàn)場或損傷點(diǎn)附近的掩蔽處實(shí)施搶修，能夠最大程度地縮短搶修時間、提高搶修的時效性[1]。

在快節(jié)奏的戰(zhàn)場上，允許戰(zhàn)場搶修的時間是有限的，有限的戰(zhàn)場搶修力量常常需要在短時間內(nèi)前出搶修多臺損傷裝備，因此承擔(dān)機(jī)動搶修任務(wù)的搶修組常常需要按照一定的順序搶修損傷裝備，搶修順序極大地影響著搶修任務(wù)完成的時效性甚至成敗，必須對其進(jìn)行科學(xué)決策。機(jī)動搶修順序的決策受到?jīng)Q策目標(biāo)、機(jī)動量和機(jī)動難度、機(jī)動安全性、搶修任務(wù)量、搶修工期等諸多因素的影響，必須采用客觀決策方法決策，盡量降低主觀決策容易帶來的潛在風(fēng)險(xiǎn)[2-5]。

目前，研究者已經(jīng)針對不同類型裝備提出了不少相關(guān)的戰(zhàn)場搶修決策優(yōu)化方法。田冕[2]采用層次分析法、劉利[3]采用貝葉斯網(wǎng)絡(luò)理論、何曉暉[4]采用模糊理論提出了相應(yīng)的多裝備搶修順序決策方法。王雷在考慮搶修時限的條件下提出了搶修順序決策方法，但該模型未從指揮角度區(qū)分裝備搶修時限的個體差異性，影響了決策的合理性。針對這一不足，本研究考慮單裝搶修時限因素，對搶修順序決策優(yōu)化模型進(jìn)行研究。

1 戰(zhàn)場機(jī)動搶修決策問題分析

1.1 問題描述

假設(shè)機(jī)動搶修組預(yù)先編成并作為一個整體序貫地?fù)屝迵p傷裝備。因此從理論上可以將機(jī)動搶修決策問題視為路徑尋優(yōu)問題，典型的旅行商問題以路徑最短為目標(biāo)進(jìn)行路徑?jīng)Q策，而戰(zhàn)場搶修決策影響因素不僅包括搶修組與各損傷裝備以及損傷裝備之間距離的影響，而且與路線受威脅程度、任務(wù)量、器材備件滿足程度以及搶修時限等因素緊密相關(guān)，因此決策模型也較復(fù)雜[5]。

問題描述：假設(shè)1個搶修組由其所屬位置出發(fā)，在戰(zhàn)場進(jìn)行巡回?fù)屝蓿僭O(shè)戰(zhàn)場共有包含搶修組出發(fā)位置的n個搶修點(diǎn)，以1,2,…,n來表示，其中1為出發(fā)點(diǎn)，其他為搶修點(diǎn)。定義機(jī)動搶修頂點(diǎn)向量V，V=(v1,v2,…,vi,…,vn)，其中，vi為機(jī)動搶修路線上的第i個搶修點(diǎn)。定義機(jī)動時間矩陣Y，Y={yij|vi,vj∈V}，其中i，j分別為機(jī)動路線的起止點(diǎn)。定義搶修時間向量P=(p1,p2,…,pi,…,pn)，其中pn是第n個搶修點(diǎn)的搶修耗時，假設(shè)每個搶修點(diǎn)對應(yīng)確定的搶修任務(wù)，每個搶修點(diǎn)所需的搶修資源以及搶修時間是確定的，即P為常值向量。定義搶修時限向量D=(d1,d2,…,di,…,dn)，其中di是第i個搶修點(diǎn)的搶修任務(wù)時限，即該搶修點(diǎn)允許的最晚修竣時間。

定義E={(vi,vj)|vi,vj∈V，i≠j}，E為連接各頂點(diǎn)邊的集合，表示搶修點(diǎn)間的機(jī)動巡回路線。機(jī)動搶修的巡回路線為一條起止均為v1的閉合回路，v1為機(jī)動搶修組的出發(fā)點(diǎn)，搶修組在遍歷搶修點(diǎn)之后重新返回出發(fā)點(diǎn)v1。

1.2 決策目標(biāo)

機(jī)動搶修決策的目標(biāo)主要是滿足作戰(zhàn)需求，即盡量降低對作戰(zhàn)時間的影響，常用的目標(biāo)有：搶修總耗時最短或維修點(diǎn)的待修延誤時間最短。如果決策目標(biāo)不考慮維修時限對搶修行動的影響，僅考慮搶修總耗時最短，由于各搶修點(diǎn)搶修耗時為確定值，所以搶修總耗時最短問題，即等價(jià)為搶修巡回路線最短問題，即在網(wǎng)絡(luò)圖G中尋找一條路徑，該路徑經(jīng)過每個頂點(diǎn)且只經(jīng)過一次，目標(biāo)是使該路徑上的機(jī)動時間之和最小。這是一個典型的旅行商問題(Traveling salesman problem，TSP)，在圖論中屬于Hamilton圈問題，是一種NP完全的組合優(yōu)化問題，可用分枝定界、0-1規(guī)劃、蟻群算法或遺傳算法等解析或智能算法進(jìn)行求解。但是由于需要考慮搶修時限的影響，即單純以搶修總耗時最小并非決策者的唯一關(guān)注點(diǎn)，以恢復(fù)戰(zhàn)斗力為目標(biāo)的戰(zhàn)場搶修，必須在戰(zhàn)術(shù)允許的時間內(nèi)修竣損傷裝備，即搶修時限是不可忽視的決策影響因素。為此在決策目標(biāo)中引入搶修時限因素[6]。

搶修時限因素可以為硬約束或軟約束，硬約束即表示不接受搶修完成時間超出搶修時限的事件發(fā)生，而軟約束則以搶修完成時間超出搶修時限的總延誤時間最短，則硬約束可視為軟約束的一種特殊情況，若軟約束條件下最優(yōu)決策方案能夠滿足硬約束，表示硬約束條件下該問題可解，否則表示該問題無解。

定義步時間矩陣S={sij}，其中i，j=1，2，…，n；i≠j；sij=yij+pj，sij表示搶修組從vi出發(fā)直接到達(dá)vj并完成在vj的搶修任務(wù)的“一步”所需要的時間。

對于軟約束來說，決策目標(biāo)是使搶修總耗時和搶修延遲時間都最短，這兩個目標(biāo)值常常無法同時達(dá)到最優(yōu)。為此在目標(biāo)函數(shù)中引入系數(shù)，將兩個目標(biāo)值進(jìn)行線性融合。對于V的一個巡回次序C={c1，c2，…，ci，…，cn}，其中ci∈V(i=1，2，…，n)，則有模型：

(1)

λ1+λ2=1

(2)

式中，λ1和λ2分別表示巡回路線最短和延遲時間最短這兩個目標(biāo)的相對權(quán)重，通常由決策者預(yù)先給定。

2 決策求解算法

由第1節(jié)可知，機(jī)動搶修順序決策問題實(shí)際上屬于有約束的TSP問題，目標(biāo)函數(shù)不僅考慮步序的問題，而且考慮到了延遲時間最短這一目標(biāo)，用于解決典型TSP問題的許多模型和方法都不再適用，為此采用智能尋優(yōu)算法進(jìn)行路徑尋優(yōu)，本文采用遺傳算法求解上述模型[7-8]。

遺傳算法(Genetic Algorithm，GA)是模擬生物遺傳學(xué)中自然選擇和迭代進(jìn)化過程的智能尋優(yōu)算法，它具有廣泛的適應(yīng)性，對于求解復(fù)雜TSP問題有著顯著的效果。

1) 編碼方案

按巡修路線上的維修點(diǎn)順序進(jìn)行編碼，即染色體中的每個基因代表一個維修點(diǎn)的編號。由于搶修出發(fā)點(diǎn)已經(jīng)確定，即染色體首位皆為1，因此以實(shí)際搶修點(diǎn)編碼序列構(gòu)造染色體，染色體長度為n-1，采用隨機(jī)排序數(shù)列生成函數(shù)構(gòu)造染色體，采用實(shí)值編碼。

2) 適應(yīng)度函數(shù)

初始種群根據(jù)編碼規(guī)則隨機(jī)產(chǎn)生一代個體，根據(jù)每個染色體的表現(xiàn)計(jì)算出目標(biāo)函數(shù)值，將第j個染色體對應(yīng)目標(biāo)函數(shù)值記為Tj，將個體j的適應(yīng)度定義為：

(3)

其中，N為遺傳種群的規(guī)模，即一代染色體的數(shù)量。

為了有效地控制求解過程的效率，對染色體適應(yīng)度值進(jìn)行過程修正，修正后的適應(yīng)度表示為f′(j)，則有：

(4)

式中： max(Tj)為本代個體的最大目標(biāo)函數(shù)值；η為適應(yīng)度系數(shù)，η取值越小，淘汰率越高，收斂速度越快，這里采用變適應(yīng)度系數(shù)的策略，從0.95到0.15遞減取值，以防止過早收斂，無法求得全局最優(yōu)解。

3) 選擇算子

為確保種群進(jìn)行全局尋優(yōu)，采用輪盤賭的方法產(chǎn)生新一代種群，然后進(jìn)行交叉和變異操作。

4) 雜交算子

雜交算子采用順序交叉的方法，即隨機(jī)確定交叉段的起止點(diǎn)位置，對中間段的基因進(jìn)行交叉操作。為了確保交叉之后的染色體仍然對應(yīng)可行解，在被交叉的兩個染色體中隨機(jī)選中一段長度隨機(jī)的基因串，進(jìn)行交叉操作，對基因串進(jìn)行檢驗(yàn)和調(diào)換，交叉操作方法示意圖如圖1所示。

如圖1所示，在染色體b中找到將染色體a中被選中的基因段{6，4，5}的位置，按照{(diào)6，4，5}的順序進(jìn)行重新排序并插回原染色體，同樣，在染色體a中找到染色體b中被選中的基因段，做相同操作，交叉前后的基因段則都能夠?qū)?yīng)決策可行解。

5) 變異算子

變異算子采用雙位變異操作模式，在個體染色體中隨機(jī)抽取2個基因位進(jìn)行交換而產(chǎn)生新的個體。

6) 進(jìn)化策略

考慮到選擇算子和交叉算子的迭代擇優(yōu)效率不高，為了保存進(jìn)化成果，每一代經(jīng)過選擇、交叉和變異操作后都保留當(dāng)代最優(yōu)個體，剔除最差個體，以保證算法具有全局收斂性。

3 應(yīng)用實(shí)例

假設(shè)在某次聯(lián)合進(jìn)攻戰(zhàn)役過程中，我數(shù)字化合成部隊(duì)與當(dāng)面之?dāng)痴归_攻防作戰(zhàn)，在正面作戰(zhàn)方向上，數(shù)字化合成部隊(duì)所屬兩個合成作戰(zhàn)營作為第一梯隊(duì)在炮兵防空兵掩護(hù)下，突破敵永久防御攻勢向縱深發(fā)展，由于受敵地雷和反坦克武器的攻擊，第一梯隊(duì)報(bào)告坦克和步兵戰(zhàn)車共戰(zhàn)損15臺，受前方指揮所指示，后方指揮所決定派出一支搶救搶修隊(duì)立即前出進(jìn)行戰(zhàn)場搶修。

已知各戰(zhàn)損裝備的待修位置，前方搶修力量已經(jīng)完成損傷的初步評估，預(yù)測得出各單裝的現(xiàn)地?fù)屝薰r，如表1所示，各搶修點(diǎn)之間的距離換算為時間，如表2所示，為了保證進(jìn)攻的持續(xù)性，前方指揮所對各臺裝備的修竣時限提出了要求，如表3所示。后方指揮所要為搶救搶修隊(duì)規(guī)劃搶修路線，目標(biāo)是使得戰(zhàn)損裝備總延誤時間最小。

表1 損傷裝備現(xiàn)地?fù)屝薰r min

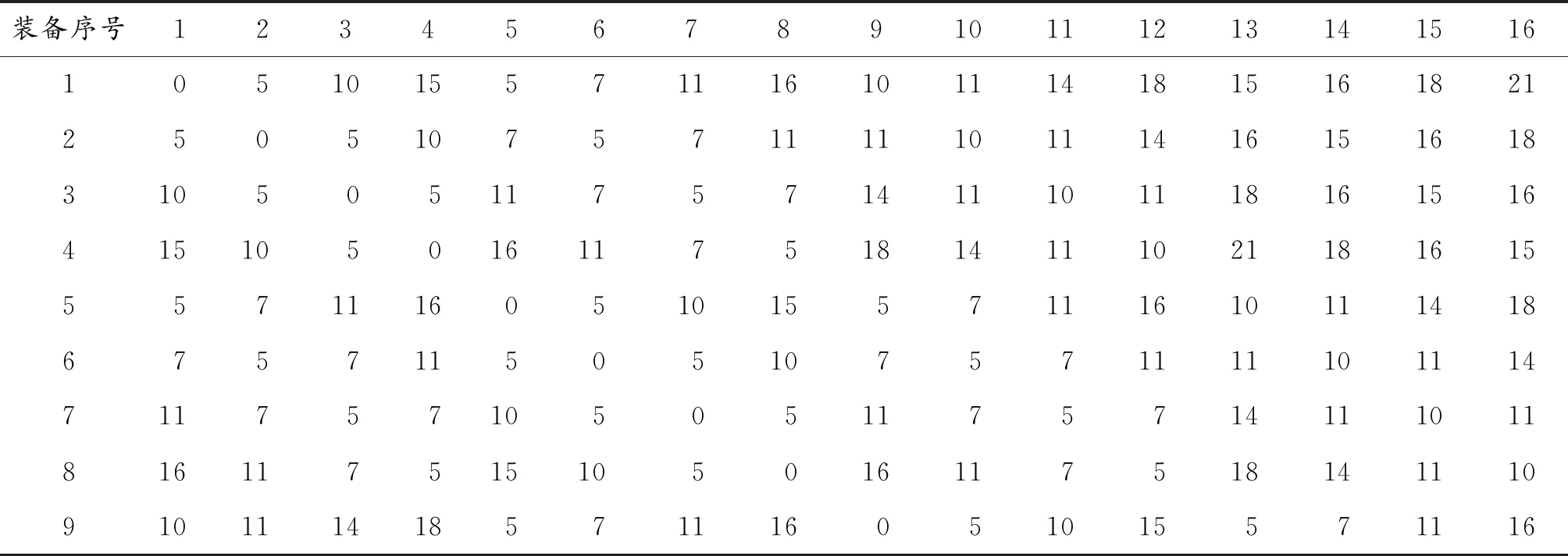
表2 損傷裝備之間的距離 min

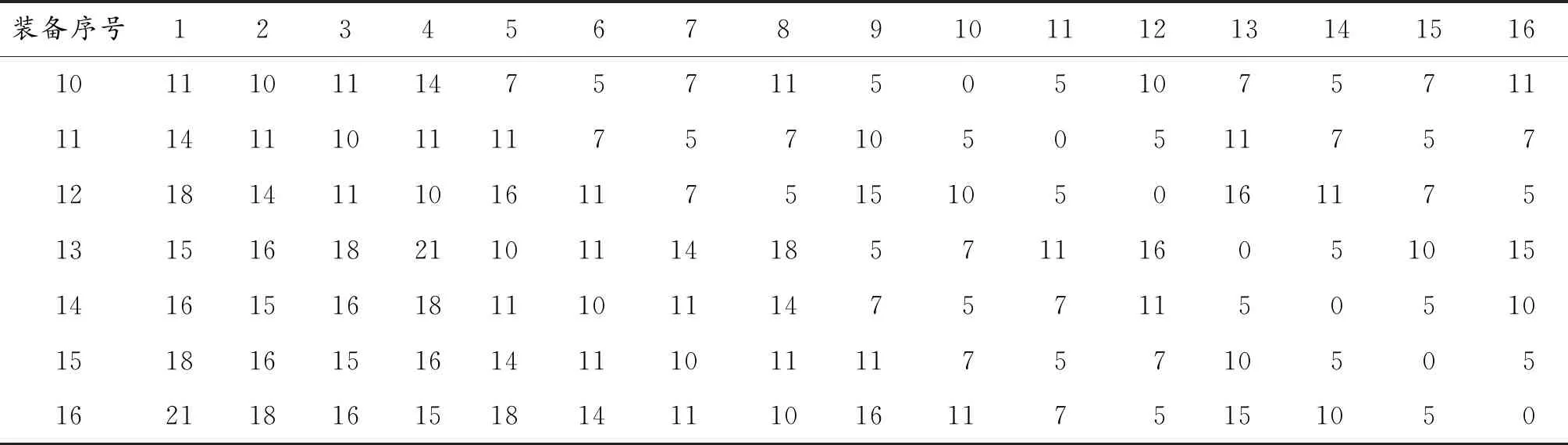
續(xù)表(表2)

表3 損傷裝備修竣時限 min

應(yīng)用Matlab編寫遺傳算法求解程序，進(jìn)行決策優(yōu)化求解，主要計(jì)算過程如下：

1) 利用表1～3中的數(shù)據(jù)得到步時間矩陣和修竣時間矩陣，給定λ1和λ2的值，設(shè)定遺傳算法參數(shù)，隨機(jī)生成初始種群。

2) 根據(jù)式(4)計(jì)算初始種群中各個個體的適應(yīng)度值。

3) 根據(jù)設(shè)定的種群保留概率隨機(jī)生成相應(yīng)數(shù)量的子代個體，根據(jù)輪盤賭的策略選擇父代個體組成新種群。

4) 根據(jù)雜交概率進(jìn)行交叉操作。

5) 根據(jù)變異概率進(jìn)行變異操作。

6) 根據(jù)當(dāng)次種群保留概率用當(dāng)代最優(yōu)個體替換最差個體。

7) 更新群體，用新種群替代父代種群，更新種群保留概率。

8) 判斷是否達(dá)到最大遺傳代數(shù)或代際適應(yīng)度最優(yōu)值變化值低于閾值，則算法終止并輸出最優(yōu)結(jié)果；否則轉(zhuǎn)第2)步。

根據(jù)案例中決策問題的特點(diǎn)，設(shè)定λ1=0.3，λ2=0.7，設(shè)定遺傳算法參數(shù)為：群體規(guī)模為50，最大迭代次數(shù)為 2 000，適應(yīng)度系數(shù)為0.95，種群初始保留概率為0.95，雜交概率為0.7，變異概率為0.25。

按照上述參數(shù)進(jìn)行決策求解，求解過程如圖2所示，由圖2可知，在約300次迭代后，最優(yōu)解即收斂到最優(yōu)值。

得到最佳的巡修路線為：

{1→9→6→2→3→4→8→12→16→15→11→7→5→10→14→13}

按照該巡修路線實(shí)施搶修，本次任務(wù)預(yù)計(jì)耗時 1 184min。但由于作戰(zhàn)需求，無法在給定搶修時限內(nèi)完成全部搶修任務(wù)，各搶修任務(wù)的修竣時間與修竣時限的對比圖如圖3所示。

如圖3所示，對于個搶修點(diǎn)來說，若修竣時間低于修竣時限，表示及時完成了該任務(wù)，此類事件越多，越符合決策者的需求。由圖中可知共有5個搶修任務(wù)及時完成，分別為任務(wù)9、6、2、3、4。由于采用式(1)中的決策目標(biāo)函數(shù)，綜合了搶修總時間和搶修延遲時間最短這兩類目標(biāo)，因此該決策解是權(quán)衡這兩類目標(biāo)的最優(yōu)解，與λ1和λ2的取值有關(guān)。

當(dāng)λ1=1，λ2=0時，則決策目標(biāo)為搶修總時間最短，當(dāng)λ1=0，λ2=1時，則決策目標(biāo)為搶修總延誤時間最短。

按照上述參數(shù)進(jìn)行求解，可分別得到兩種情況下的最優(yōu)決策解，將圖2所示方案標(biāo)識為方案1，結(jié)果如表4所示。

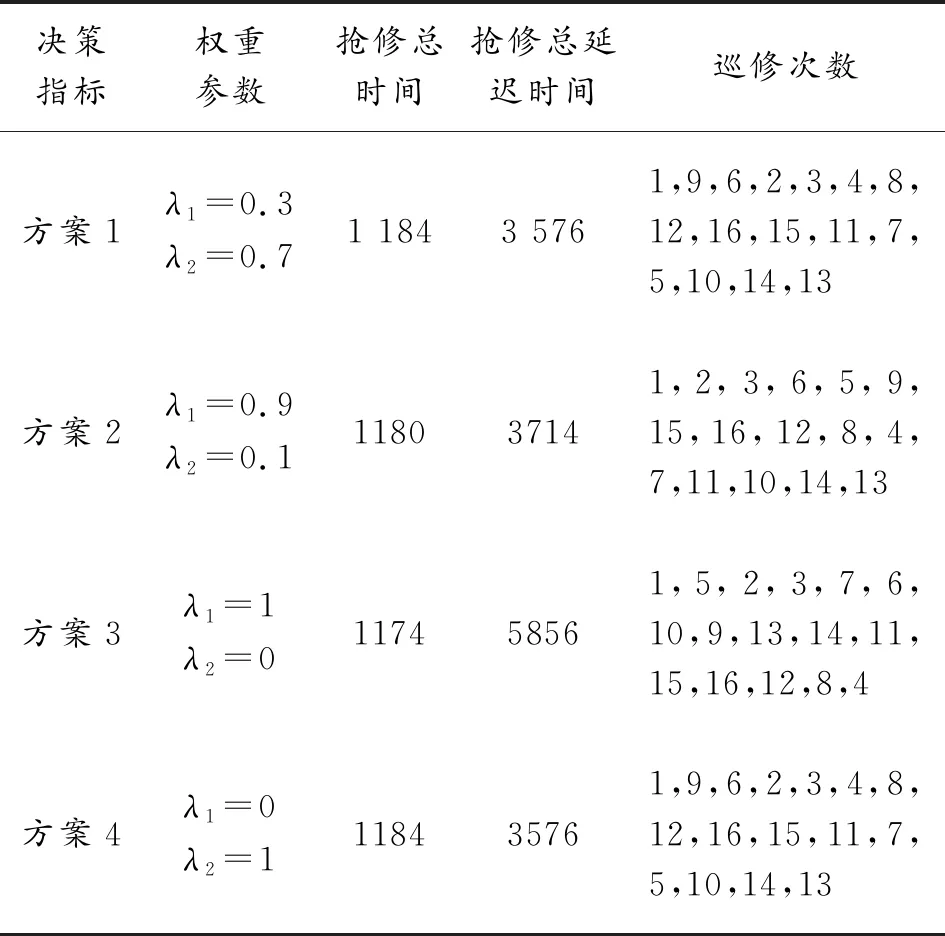
表4 不同條件下巡修路線決策最優(yōu)解 min

由表4所示數(shù)據(jù)可知，若僅以搶修總時間最短為目標(biāo)，則搶修總時間最小可達(dá)到1 173 min，若僅以總延誤時間最短，該值最小可達(dá)到3 576 min，若λ1和λ2取0～1之間數(shù)值的話，則這兩類指標(biāo)將得到權(quán)衡。

4 結(jié)論

在信息化戰(zhàn)爭條件下，對于有限的戰(zhàn)場搶修力量來說，戰(zhàn)場機(jī)動搶修順序決策直接關(guān)系著搶修人員的安全性和搶修效益。在戰(zhàn)術(shù)允許的時間內(nèi)完成搶修，是作戰(zhàn)指揮員關(guān)注的重點(diǎn)，必須綜合考慮總搶修時間與搶修延遲時間，使戰(zhàn)場搶修效益最大化。由于搶修行動本身在資源消耗、時間消耗上存在較大的不確定性，本文對其進(jìn)行了簡化處理，在下一步的研究中，有必要針對單裝搶修時間與資源的隨機(jī)特性確定最優(yōu)的搶修順序。