基于最小二乘支持向量機的氧化鋁濃度預測
崔家瑞,張政偉,李 擎,崔家山
(北京科技大學, 北京 100083)
在電解鋁的生產過程中,氧化鋁濃度是決定其生產過程各項技術指標的關鍵參數,當電解質的氧化鋁濃度過高,繼續下料添加氧化鋁會造成氧化鋁原料在電解槽槽底沉淀,電阻增大,電流效率變低,影響鋁電解的正常生產,氧化鋁濃度過低時,電解槽又會發生陽極效應,槽電壓劇烈上升,電解槽的能量平衡被破壞,降低出鋁量[1]。因此,為保證電解槽高效生產,必須嚴格控制電解槽內氧化鋁濃度在1.5%~3.5%范圍內[2]。
曹阿林等[3]通過確定鋁電解槽電壓與氧化鋁濃度間的關聯關系,并繪制出鋁電解槽的控制曲線,為實現鋁電解過程中氧化鋁濃度的控制提供理論依據;林景棟等[4]針對鋁電解過程氧化鋁濃度判斷困難的問題,提出基于線性回歸預測與正交變換預測法,給出槽電壓、電解槽狀態和出入量三個輸入量來預測氧化鋁濃度;張瑜等[5]釆用軟測量技術來估計氧化鋁濃度,運用徑向基函數神經網絡構建軟測量的數學模型估計出氧化鋁濃度,從而實現氧化鋁濃度的在線檢測;呂函珂等[6]綜合利用模糊解耦、模糊推理方法,根據槽電壓判定當前濃度值,同時建立氧化鋁濃度正交變換預測判定模型;張森等[7]利用陽極導桿電流和兩極壓降運用ELM算法成功預測了氧化鋁濃度,但這些方法預測的氧化鋁濃度誤差依舊較大,因此如何提高測量精度依舊是一個重要的研究方向。
在國家863項目《鋁電解生產在線檢測與MES系統關鍵技術研究及應用》基礎上,利用現場一組導桿采集到的100組數據,研究了如何實現氧化鋁濃度的在線測量。
1 軟測量依據
鋁電解過程中可直接采集的數據主要有槽電壓、下料間隔、槽電阻、溫度等,這些參數都對電解槽氧化鋁濃度有一定影響,然而最直接、最快速的參數還是槽電阻。
1.1 槽電阻
槽電阻和氧化鋁濃度之間存在某中“U”型關系[8],如圖1所示,由此在生產過程中可以通過觀測槽電阻來獲得氧化鋁濃度的相關信息。
圖1將槽電阻與氧化鋁濃度的對應關系分為4個區:高含量區:電阻對濃度變化十分敏感,但氧化鋁濃度過高會造成槽底沉淀;不敏感區:電阻對含量的變化不敏感,電流效率低;可控制區:電阻對濃度變化較為敏感,而且電流效率較高,工業氧化鋁濃度理想控制區;多效應區:氧化鋁含量很低,隨氧化鋁濃度下降電阻急速升高,極易出現陽極效應現象。
在鋁電解過程中,盡量把濃度控制在可控制區,通過測量槽電阻,依據槽電阻和氧化鋁濃度的關系,達到間接測量氧化鋁濃度的目的。
廣義上來講,電解槽的槽電阻可以從整體的角度得到:
(1)
式(1)中:Ri為第i時刻鋁電解槽的槽電阻(mΩ);Ui為第i時刻鋁電解槽的槽電壓(V);Ii為第i時刻鋁電解槽的系列電流(kA);B為表觀反電動勢,通常都看做一個固定的值,但由于每個鋁電解廠的電解槽結構或者系列電流不同,會造成表觀槽電阻略有不同,其值一般在1.6~1.7 V之間波動。
1.2 陽極導桿電流
陽極導桿電流能夠直接反映電解槽內部阻抗,即與氧化鋁濃度和極距均有一定的關系。由于每根陽極導桿的電流在6~8 kA左右,無法直接在線測量,針對此問題,采用等距壓降法測量陽極導桿電流。
等距壓降法測量電流就是在陽極導桿上選取一段固定的導桿,采用硬件設備測量該段導桿的電壓值,然后采用歐姆定律計算電流[9]。即:
在電解過程中,陽極導桿的溫度是實時變化的,這就導致了陽極導桿電阻率的變化,陽極導桿實際電阻為
(2)
式(2)中:α為電阻率溫度系數;ρ為電阻率;L為等距壓降測量點之間的距離;S為陽極導桿橫截面積;T為導桿測點表面的溫度。
1.3 兩極電壓
兩極電壓是指陽極導桿夾具觸點到陰極鋼棒之間的電位差,比槽電壓更能快速反應各陽極導桿下的氧化鋁濃度變化情況,如圖2所示。
槽電壓除了受電解槽本身槽況的影響之外,很大程度上還會受限于整流所提供的直流電,直流電會出現各種意外情況或者波動,造成槽電壓的變化情況不能直觀反映槽況。
因此,只需要測量陽極導桿電流和兩極電壓,即可借助槽電阻得到氧化鋁濃度,并克服了槽電壓波動的影響。
2 氧化鋁濃度預測方法
由上一章可知,陽極導桿電流和兩極電壓與氧化鋁濃度之間存在某種非線性關系,在數據波動較小的情況下,最小二乘支持向量機[10](英文名稱,LSSVM)可以很好做出回歸分析。因此,將陽極導桿電流和兩極電壓作為模型的輸入,氧化鋁濃度作為輸出,可以建立與實際情況相符合的模型。
2.1 最小二乘支持向量機建模
利用在線監測終端同步采集陽極導桿電流和兩極電壓,與此同時,通過人工采集氧化鋁,并在實驗室離線測量,得到氧化鋁濃度。最后,通過將陽極導桿電流、兩極電壓與離線氧化鋁濃度對標,得到了100組有效數據。采集裝置如圖3所示。
由于采集的陽極導桿電流、兩極電壓和氧化鋁濃度數據之間存在不同的量綱,因此各類數據均需按下式對訓練樣本數據進行歸一化處理:
由于導桿電流與氧化鋁濃度存在一定的非線性,而最小二乘支持向量機可以很好解決非線性問題,因此,采用最小二乘支持向量機方法進行預測。
回歸問題中,對于給定的n維輸入t維輸出的訓練樣本集D={(xi,yi),i=1,2,…,m},可以利用非線性映射到高維特征空間,即
(3)
根據結構風險最小化原理,將式(3)表示為一個等式約束的優化問題:
(4)
式(4)中:J(ωj,eij)為結構風險函數;eij為模型預測值和真實值之差;γ為懲罰因子。
為了求解上述問題,需要將此約束問題轉換為無約束優化問題,為此需要引入拉格朗日乘子向量,建立拉格朗日等式方程,優化問題變為
L(ωj,bj,αij,eij)=J(ωj,eij)-
(5)
根據最優化理論的KKT條件,分別對式(5)中的(ωi,bj,eij,αij)求偏導,轉化為求解方程:
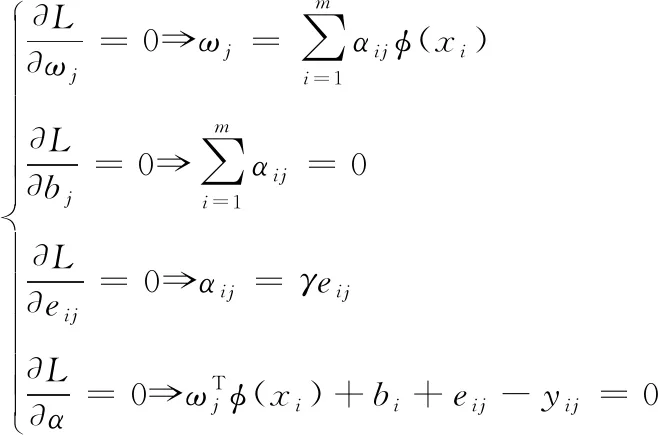
(6)
消去ω和eij,式(6)重寫為
(7)
式(7)中,K(·,·)是核函數,滿足Mercer條件
K(xi,xj)=φ(xi)φ(xj)
求解式(7)方程組,得到最小二乘支持向量機(LSSVM)模型為
綜上,將歸一化后的陽極導桿電流和兩極電壓作為最小二乘支持向量機的輸入,氧化鋁濃度作為模型輸出,進行訓練。
2.2 模型參數尋優
對于最小二乘支持向量機而言,超參數的取值與學習數據樣本集以及研究對象密切相關。懲罰因子γ值越大則允許的誤差越小,越小則允許的誤差變大。數據樣本的輸入范圍很大,就需要增大核函數寬度σ2的取值:反之,則需要減小核寬度的取值。
LSSVM模型的性能選擇取決于其核函數和2個超參數的選擇。核函數選取RBF函數[11-12],取合適的懲罰因子γ和核函數寬度σ2,是建立最小二乘支持向量機預測模型的關鍵,采用網格搜索和交叉驗證[13-15]的方法選擇LSSVM參數。
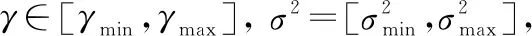
K折交叉驗證的步驟:
① 不重復抽樣將原始數據隨機分為k份;
② 將其中k-1份數據集用于訓練,剩下的1份用于測試;
③ 重復第二步k次,在每個訓練集上訓練后得到一個模型,用這個模型在相應的測試集上測試,計算并保存模型的評估指標;
④ 計算k組測試結果的標準差作為模型精度的估計,并作為當前k折交叉驗證下模型的性能指標。
3 仿真實驗
對貴州某現場230 kA預焙陽極1號車間A1導桿測量采集100組數據,進行歸一化處理,利用Matlab 2013軟件進行編程,將100組數據采用LSSVM算法進行建模,核函數采用徑向基核,由網格搜索(γ和σ2有35組參數組合)和交叉驗證驗證(80組數據進行訓練,20組數據進行驗證)方法得到氧化鋁濃度預測的標準差如圖4所示。
由圖4可知,γ和σ2的參數組合在第19組氧化鋁濃度預測值標準差最小,RMSE=0.132 1,得出該出懲罰因子為γ=10,核函數σ2=1。
模型參數確定(γ=10,σ2=1)后,得出在該組參數下訓練的各個樣本集的結果,分別如圖5和圖6所示。
由圖5可知,算法模型能夠很好地擬合實際生產數據;由圖6可知,氧化鋁濃度整體平均相對誤差為0.051 2,個體相對誤差大都在0.05附近。
采用平均相對誤差和均方根誤差作為評價標準,平均相對誤差計算公式為
均方根誤差RMSE計算公式為
其中N為測試樣本個數;y為真實值;yi為模型輸出值。
將仿真結果與文獻[5]的ELM算法進行比較,仿真結果如表1所示。

表1 算法性能比較
由表1可知,本文所提方法與文獻[5]相比,在RMSE保持基本不變的基礎上,整體平均誤差降低了22%,測量精度得到了進一步提高。
4 結論
提出了一種基于最小二乘支持向量機回歸模型的氧化鋁濃度軟測量方法。該方法將易在線測量的陽極導桿電流、兩極電壓作為模型輸入,采用網格搜索和交叉驗證的方法得到模型最優超參數,提升軟測量精度;基于現場采集的數據,驗證了所提方法的有效性。雖然所提方法能夠實現氧化鋁濃度的軟測量,但在實際應用中還需進一步提高實時性和穩定性。

