行進間火炮指向穩定跟蹤系統建模與控制

李偉， 姜俊峰， 任海波， 張光輝

(1.西北機電工程研究所， 陜西 西安 712099；2.浙江大學 浙江省先進制造技術重點實驗室， 浙江 杭州 310027)

0 引言

自行火炮具備行進間穩定瞄準跟蹤射擊能力是新軍事斗爭的迫切需求。火炮在穩定系統控制下，與坦克或突擊炮的火炮控制系統功能相似，不但要克服載體姿態變化對火炮指向的擾動，而且需具有足夠的帶寬跟隨火力控制解算的射擊諸元，但坦克屬于直瞄武器，其射角低于20°，方位功率只有幾千瓦。類似設備如光電視線跟蹤因其負載小、響應快，穩定系統不局限于某種載體平臺，且在其高低角全范圍都能達到較高精度[1-5]。自行火炮射角約為85°，隨著射角增大，方位穩定系統所需功率急劇增大[6]，才能克服載體姿態擾動。同時，火炮轉動慣量大、質量大，并存在較大不平衡力矩、傳動齒隙和剛度等因素對火炮穩定系統產生較大影響。

自行高炮行進間射擊時，火炮既受到射擊力作用，同時又受到行駛中由于地面不平度而造成的路面激勵作用及發動機振動，尤其路面不平度導致車體顛簸，造成炮口振動是影響精度的主要因素。因此，自行高炮在行進間射擊時必須有合理的車速及較好的路況條件[7]需求，極大地限制了其機動性和作戰能力。傳統自行高炮采用解算式穩定，由火力控制系統隨時修正車體姿態造成的射擊偏差，首先解算以火炮為原點的水平坐標系下射擊諸元，再轉換至載體坐標系下的射擊諸元，作為火炮隨動跟蹤指令，由等效閉環的隨動在載體坐標系內穩定火炮指向。這種方式造成火炮穩定響應滯后，難以適應車體姿態快速變化。艦炮穩定與自行高炮類似，對大噸位艦船，由于艦船搖擺周期較長，姿態擾動能量主要集中在低頻段，相對較易實現，對小噸位艦艇仍面臨自行高炮所面臨的難題。

隨著捷聯慣性導航系統(SINS)技術的進步，其航姿測量精度、長期穩定性和抗沖擊能力等性能大幅提高，且成本較低。將SINS安裝在自行火炮身管上直接測量火炮在大地坐標系的指向進行瞄準已是現代自行火炮的成熟技術，火力控制彈道解算可給出大地坐標系下的射擊諸元[8]。自行火炮隨動系統將SINS的航向和俯仰角作為其角度反饋，實現了火炮在大地坐標系下的全閉環直接控制，提高了火炮瞄準精度。傳統方式控制下，因為火炮調轉運動與SINS測量坐標不統一，造成高低和方位隨動控制系統存在耦合，影響瞄準的快速性。對于只能駐停間發射的自行火炮可靈活采用四元數、歐拉角法等坐標變換或串級控制來解決。而對于行進間瞄準射擊的自行火炮需采用既能抑制載體擾動，又能很好解決控制耦合下的穩定跟蹤瞄準問題的新方法。

在火炮指向的動力學分析、控制方法和策略等研究中，系統建模技術具有重要作用。田建輝[9]對火炮身管指向定位和跟蹤控制方法進行了理論分析，但動力學建模上沒有考慮載體運動導致的載體、炮塔與火炮控制三者軸間的耦合力矩，忽略了各轉動部件的重心偏移，控制上忽略了執行機構和傳動機構特性，工程實用性不強。于存貴等[10]利用虛擬樣機技術和艦船耐波性理論，對艦載火箭炮調炮運動進行動力學建模仿真，計算了某艦載火箭炮在艦船搖擺情況下調炮時方位和高低傳動的受力情況，但艦載火箭炮系統建模過于簡化，難以體現控制軸間速率干擾和力矩干擾的細節情況。葉鐳[11]考慮了載體姿態擾動后，利用機器人建模方法，對無人炮塔的火炮控制系統建立了炮塔與火炮耦合動力學模型、坦克1/2車體懸掛系統模型及路譜激勵，針對行進間火炮指向研究了非線性控制方法，但所建模型沒有體現火炮與車體之間的關聯性，仍然采用坐標變換位置的解算式穩定方法。在主戰坦克火炮穩定控制器的研究方面，Karayumak[12]考慮了坦克身管彈性、傳動系統各個環節的多自由度被控對象模型，研究了炮口速率觀測和速率反饋穩定，干擾速率前饋補償控制等方法。在不平路況和正弦路面對車體擾動的環境下進行仿真，火炮穩定精度達到了0.5 mrad，但系統控制并未考慮電機執行機構模型及車體姿態耦合擾動情況。在火力控制解算的坐標系選擇上，鄭巖等[13]研究發現，坦克火力控制采用大地坐標系下解算，能反映出目標與坦克之間的絕對運動關系，不但能提高對目標的預測精度，并且大大縮短了預測時間。

針對采用SINS測量火炮指向的自行火炮，充分利用SINS測量火炮指向和SINS陀螺測量火炮三軸向運動的優勢，提出火炮在大地坐標系下完成穩定控制的方法。釆用Lagrange方法建立火炮、炮塔雙軸與載體六自由度運動狀態之間的耦合模型，并考慮炮塔和火炮回轉中心與重心不重合等因素，用于驗證穩定控制方案、系統控制策略等。最后建立系統的控制仿真模型，并驗證了本文穩定控制方法的有效性。該方法為SINS測量火炮指向的火炮動基座條件下的通用穩定控制方法，不針對某種特定平臺，不局限于某種可移動載體平臺。

1 坐標系定義

火炮身管俯仰部分在高低驅動電機帶動下在炮塔上作俯仰運動，炮塔在方位驅動電機帶動下在運動載體上作方位回轉運動，從而使火炮跟隨控制指令指向目標，如圖1所示。該俯仰和回轉運動模型為雙軸動力學模型，為了簡化系統分析，假設火炮、炮塔聯動狀態下不影響車體運動狀態。

由圖1可知，本文所涉及的坐標系包括大地坐標系、平動坐標系、載體坐標系、炮塔坐標系和火炮身管俯仰部分坐標系。大地坐標系Ogxgygzg與大地固結不動，將原點Og定為載體初始質心處，Ogxg軸平行于水平面指向正北，Ogyg軸平行于水平面指向正東，Ogzg軸垂直水平面向下，載體在該坐標系下的坐標為(x，y，z). 載體坐標系Ocxcyczc的原點Oc位于載體搖擺中心(取重心處)，Ocxc軸沿載體縱軸指向前方，Ocyc軸沿載體橫軸指向右側，Oczc軸垂直載體縱軸、橫軸指向下方。載體在載體坐標系下的角速率坐標為(p,q,r)，速度坐標為(u,v,w).平動坐標系Omxmymzm原點Om與載體坐標系原點Oc重合，Omxm軸與Ogxg軸指向一致，Omym軸與Ogyg軸指向一致，Omzm軸與Ogzg軸指向一致。炮塔坐標系Ohxhyhzh原點Oh為炮塔方位回轉軸與方位回轉平面的交點，Ohxh軸為火炮身管軸線向炮塔方向回轉平面的投影指向彈丸射向，Ohzh軸沿炮塔方向回轉軸指向下與Oczc軸平行，Ohyh軸垂直于Ohxh軸與Ohzh軸構成的平面向右。炮塔坐標系原點Oh在載體坐標系的坐標為(xch,ych,zch)，炮塔質心在炮塔坐標系的坐標為(x′h,y′h,z′h).

火炮身管俯仰部分坐標系Opxpypzp的原點Op為火炮俯仰轉動軸與火炮身管俯仰平面的交點，Opxp軸與火炮身管軸線重合指向彈丸射向，Ocyc軸與耳軸重合指向炮塔右側，Opzp軸垂直于Opxp軸與Ocyc軸構成的平面指向下。火炮身管俯仰部分坐標系原點Op在炮塔坐標系的坐標為(xhp,yhp,zhp)，火炮身管俯仰部分質心在火炮身管俯仰部分坐標系的坐標為(x′p,y′p,z′p).

根據以上坐標定義，從平動坐標系變換至載體坐標系的變換矩陣

(1)

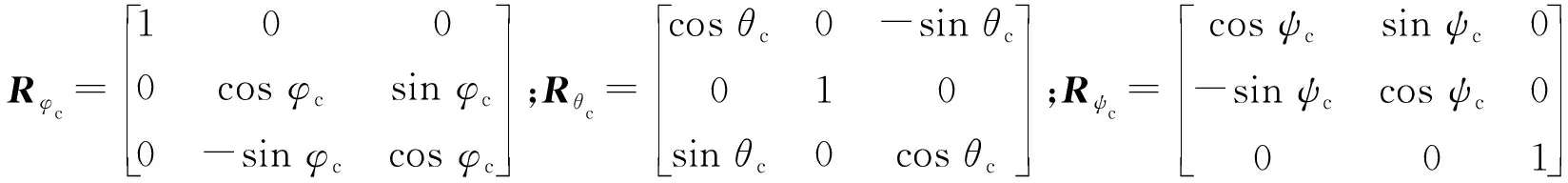
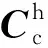
(2)

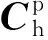
(3)

(4)

(5)

2 火炮指向雙軸動力學模型的建立

火炮穩定控制應考慮載體姿態變化對火炮指向運動控制的影響。根據第1節坐標系定義，炮塔坐標原點速度量為

(6)

炮塔質心的速度量為

(7)

火炮身管俯仰部分質心的絕對速度量為

(8)

炮塔的絕對旋轉角速率為

(9)

火炮身管俯仰部分的絕對旋轉角速率為

(10)

采用Lagrange方程法建立炮塔回轉和火炮身管俯仰部分運動的動力學模型：

(11)

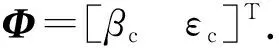
(12)

式中：ET=EThr+ETht+ETpr+ETpt；ED=EDh+EDp；EV=EhVg+EpVg+EpVk.ETht為炮塔質心動能：

(13)

式中：mh為炮塔質量。EThr為炮塔旋轉動能：

(14)

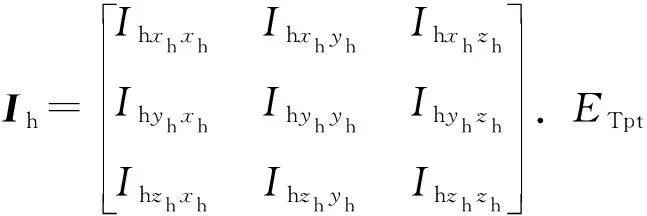
(15)

ETpr為火炮旋轉動能：

(16)

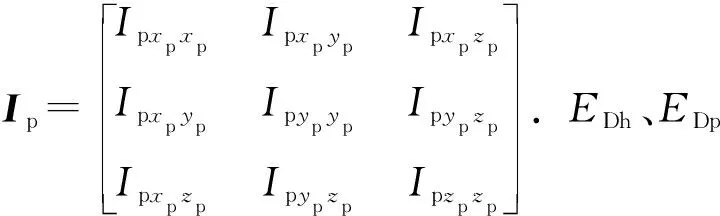
(17)

式中：Ch、Cp分別為炮塔、火炮轉軸傳動的黏性摩擦系數。EpVk為火炮的彈性勢能：

(18)

式中：Kp為彈鏈、線纜等的彈性系數。EhVg、EpVg分別為炮塔、火炮身管俯仰部分的重力勢能。

經過載體姿態的搖擺，且在炮塔和火炮調轉后，炮塔和火炮身管俯仰部分在平動坐標系下的重力勢能變化可表示為

EhVg=mhg[(-cosβcsinθc+sinβcsinφccosθc)x′h+
(sinβcsinθc+cosβcsinφccosθc)y′h+cosφccosθcz′h],

(19)

EpVg=mpg[(-cosβcsinθc+sinβcsinφccosθc)·
(xhp+cosεcx′p+sinεcz′p)+
(sinβcsinθc+cosβcsinφccosθc)·
(yhp+y′p)+cosφccosθc·
(zhp-sinεcx′p+cosεcz′p)-zch-zhp-z′p.

(20)

將(13)式～(20)式帶入(12)式后整理得到穩定系統被控對象，即火炮指向雙軸動力學模型：

(21)

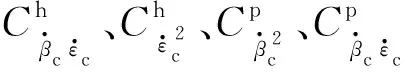
3 穩定跟蹤控制系統模型

為了驗證基于大地坐標系下的穩定控制方法，采用傳統三環控制結構，各環控制器采用傳統經典的比例積分(PI)控制方法，便于工程應用，如圖2所示。圖2中：ψref和θref分別為大地坐標系下的方位角和高低角控制主令；ihref和ipref分別為方位和高低電流環指令；ihm、ihs分別為方位主電機、從電機的電流環指令；Thme、Thse分別為方位主電機、從電機輸出的力矩；Tpe為高低電機輸出的力矩；θhmm、θhsm、ωhmm、ωhsm分別為主電機、從電機旋轉角度和角速率；θpm為高低電機旋轉角度；Thml、Thsl分別為主電機、從電機所受傳動軸的負載力矩；Tpl為高低電機所受傳動軸的負載力矩；Tc為炮塔作用于載體的三軸向力矩。虛線部分為可根據需要采用的速率干擾前饋補償控制。

系統采用三相交流永磁同步電機作為執行電機，由成熟的空間矢量脈寬調制(SVPWM)控制功率電子絕緣柵雙極型晶體管(IGBT)進行驅動。電流環采用id=0 A的矢量控制方法，利用電流環控制以得到所需力矩，其電流環PI控制器參數分別采用零極對消和期望時間常數設計方法。穩定環的PI速度控制器參數采用最佳中頻寬度的設計方法[14]，位置環采用PI控制與前饋相結合的復合控制。方位系統采用成熟的雙電機拖動協調消隙控制，同時提高傳動剛度，為實現末端速度反饋提供條件，具體可參考文獻[15].

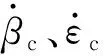
(22)

利用(22)式可避免對SINS航姿輸出值求導或進行觀測求解平動坐標系下的角速率。根據坐標系定義，平動坐標系與大地坐標系只是平移關系，對角度不產生影響。將大地坐標系作為穩定控制下靜止不動的基準坐標系，利用統一在大地坐標系下的角度反饋和速度反饋可使高低和方位控制解耦。在已知ωp、βc、εc及其變化率時，可反向推算出炮塔ωh和載體姿態干擾角速率p、q、r，為干擾前饋補償提供信息參考。雖然SINS實際航姿解算采用旋轉矢量法，但該解算過程在控制中仍然可看作是積分環節，不影響控制系統的分析。也可對(22)式進行積分求解SINS航姿角，與(5)式求解火炮身管指向等效，也為SINS安裝在載體上，為求解火炮身管指向提供了一種途徑。

4 仿真驗證

以干擾譜作為輸入的六自由度載體運動狀態模型，作為姿態擾動輸入最為理想，但運動載體姿態頻率響應函數不易得到。根據參考文獻[16]，選取擾動特征的最大幅值和主振頻點作為擾動輸入來驗證控制策略是有效的。同時按參考文獻[17]，載體六自由度運動狀態可作單頻處理為：ψc=Aψcsin (fψct+εψc)，θc=Aθcsin (fθct+εθc)，φc=Aφcsin (fφct+εφc)，Xg=10t+AXgsin (fXgt+εXg)，Yg=0，Zg=AZgsin (fZgt+εZg). 其中，Ai、fi、εi(i∈{ψc,θc,φc,Xg,Yg,Zg})分別為載體航向、俯仰、橫滾旋轉運動前右下平移運動的幅值、頻率和相位。仿真時，按參考文獻[4]提供的一種重型車輛行進間典型車體運動數據進行仿真計算。三軸旋轉幅值為7°，周期為2 s，頻率為0.5 Hz，三軸同時大幅搖擺的干擾條件惡劣，故fψc=fθc=fφc=fXg=fZg≈3.14 rad，三軸平移按AXg=1 cm,AZg=3 cm. 而極限條件是指在給定伺服驅動功率限制和最大火炮射角條件下，穩定系統所能適應的最大擾動頻率和幅值。極限條件不是恒定的，主要根據仿真需要進行調整，分別在典型條件和極限條件下進行火炮指向穩定和正弦跟蹤仿真，其結果如下。

4.1 典型載體擾動條件穩定

姿態擾動模型具有隨機性，為了簡化，設定初始相位分別為εψc=π/20 rad,εθc=π/15 rad,εφc=π/6 rad,εXg=π/5 rad，εZg=π/3 rad. 大地坐標系下的火炮穩定主令分別為ψref=166.7 mrad(約10°)，θref=1 266.7 mrad(約76°)，得到典型載體擾動條件下火炮指向穩定控制曲線如圖3所示，及其火炮速率穩定控制相關狀態曲線如圖4所示。

由圖3(a)、圖3(b)可知，采用傳統的經典控制方法，火炮載體在典型擾動情況下，其方位指向穩定精度小于0.3 mrad，高低指向穩定精度小于0.2 mrad. 二者沒有超調，而且二者的位置穩定沒有相互干擾或耦合干擾。圖3(c)、圖3(d)分別為(23)式求得的載體坐標系下火炮方位和高低運動的軌跡實際值曲線，與應用(1)式、(4)式、(5)式將火炮指向從大地坐標系向載體坐標系轉換得到的參考值曲線幾乎重合，其穩態誤差大小與穩定誤差相當。只要在大地坐標下完成高精度控制，那么火炮在載體坐標系下的實際運行角度將自動跟蹤坐標轉換的參考值。火炮指向穩定主要依靠SINS陀螺反饋的速度穩定環實現，充分發揮穩定系統速度穩定環帶寬遠寬于位置環、響應快的優勢。而傳統高炮位置解算式穩定是火炮隨動跟蹤載體坐標系下的位置主令，間接實現火炮指向穩定。位置解算式穩定是利用隨動位置環來實現穩定，顯然其帶寬不夠，因此，傳統高炮位置解算式穩定要求載體姿態擾動盡可能小。否則，將使本來就帶寬很有限的隨動無法跟蹤載體劇烈的姿態變化，要實現目標的跟蹤更難，這就是基于大地坐標系下的穩定要優于傳統高炮位置解算式穩定的根本原因。

由圖4可知，在火炮載體姿態干擾下，速度穩定環的反饋值能夠很好地跟蹤速度穩定主令，這是實現火炮指向穩定的前提條件。在穩態時，火炮在大地坐標系的角速率約為0 r/min，實現穩定。但此時在載體坐標系中電機的轉速不為0 r/min，為了克服載體擾動，而以較高的轉速做相應的適應性旋轉。表明速度穩定環具有足夠的響應帶寬來克服載體航姿擾動。在射角θref為76°時，在穩態狀態下，方位電機轉速接近最大值5 800 r/min，方位電機穩態峰值電流幾乎接近飽和值480 A，說明方位需要克服較高速度和力矩干擾，所需的功率已接近最大值，射角θref已不能再增大，再大就會超過系統調整的能力。電機三相電流值直接反映了電機軸負載變化。而高低電機穩態轉速峰值不到1 000 r/min，高低電機穩態電流較小，峰值約為25 A，高低電機需要克服較小速度和力矩干擾，所需的功率相對較小。由此可知，高射角條件下的火炮穩定，方位電機轉速高，角加速度大，方位穩定所需的功率也大。

4.2 極限載體擾動條件的穩定

減小擾動周期，增大干擾頻率，為了保持輸入干擾能量與典型條件下擾動能量相當，應減小干擾幅值。干擾參數設定為：Aψc=Aθc=Aφc=4°；周期設定為0.4 s，即頻率為2.5 Hz；fψc=fθc=fφc=fXg=fZg≈15.7 rad；其他條件不變。射角θref為1 000 mrad(約60°)，給定的方位功率不變，得到極限擾動條件下火炮指向穩定控制曲線(見圖5)和火炮速度穩定控制相關狀態曲線(見圖6)。

由圖5可知，即使車體擾動頻率增加了5倍，火炮指向穩定精度和載體坐標中的理想值和實際值的重合度較之典型條件下變化不大，穩定精度的一致性較好，實現了方位和高低系統穩定控制獨立。圖6中速度穩定反饋也能夠很好地跟蹤速度穩定指令，電機旋轉良好，能夠適應干擾頻率變化。圖6(c)中方位電機在火炮指向穩定中的峰值電流接近最大值，而圖6(d)中高低驅動在過渡過程中和穩態過程中所需的能量都大幅增加，表明高低軸受到的干擾力矩也大幅增加。

4.3 典型載體擾動條件下的穩定跟蹤

在穩定基礎上再疊加跟蹤參量，系統所需的能量進一步加大，因此所適應的擾動能力進一步受到限制。典型載體擾動條件下，大地坐標系下方位和高低跟蹤指令分別為ψref=1 000sin (2πt) mrad，θref=666.7+500sin (2πt) mrad，得到典型載體擾動條件下火炮指向正弦跟蹤控制曲線如圖7所示，及其火炮速率穩定控制相關狀態曲線如圖8所示。

由圖7可知，在該擾動條件下的火炮指向正弦跟蹤，方位跟蹤精度不大于0.5 mrad，高低跟蹤精度不大于1 mrad. 高低角在過渡過程中略有超調。在載體坐標系中，火炮運動實際值的軌跡依然能夠很好地與參考值保持一致。方位穩定和高低穩定沒有耦合。圖8中，速度穩定反饋也能夠很好地跟蹤速度穩定指令，誤差很小，幾乎重合，消除速度擾動效果明顯。高低電機的穩態電流峰值大幅增加，峰值約65 A，間接反映了在這種條件下高低負載擾動力矩增加。方位電機的電流曲線很明顯在射角θref>666.7 mrad的區間比射角θref<666.7 mrad的區間要大。整個過程方位功率比較富余。

4.4 極限條件下的穩定跟蹤

擾動條件下的正弦跟蹤，既要穩定，又要跟蹤，系統所需能量較大，其跟蹤精度受火炮射角θref影響大，因此該極限條件的穩定跟蹤與火炮指向純穩定有所不同。經過大量仿真，幅值仍取Aψc=Aθc=Aφc=7°，將周期設定為1.4 s，頻率為0.71 Hz，fψc=fθc=fφc=fXg=fZg=4.48 rad，控制器環控制參數不變，得到極限載體擾動條件下火炮指向正弦跟蹤控制曲線如圖9所示，及其火炮速率穩定控制相關狀態曲線如圖10所示。

由圖9和圖10可知，火炮指向在正弦跟蹤中，其方位和高低穩態跟蹤精度不大于1 mrad. 圖9(a)中,在0.7～1.5 s之間出現了超差情況，此時在圖9(b)中，射角θref在1 000 mrad的上方趨于頂點附近，方位電機輸出電流趨于飽和，系統缺乏相應調整適應能力。與之對應的有圖10(a)中的穩定速度曲線出現超調表明，此射角區間方位系統對高射角很敏感，射角稍微增大，功率很快達到上限。圖9(c)中，火炮在載體坐標下的運動軌跡在相應時刻也出現了誤差較大情況。而當射角θref<666.7 mrad時，方位系統所需的電流峰值下降至約105 A. 高低系統在調轉過程中一直處于電流飽和狀態，穩態由電流峰值也約為65 A，與圖8(d)相當，由此表明高低系統對載體姿態擾動變化不敏感。通過比較圖3、圖5、圖7、圖9可知，高低和方位在角度穩定跟蹤控制中，二者之間的耦合干擾不明顯。

以上仿真驗證了該穩定控制模型的有效性。后續將輪式車輛、履帶車輛、兩棲車輛行進間顛簸或搖蕩的實際運動狀態作為模型的隨機干擾輸入，來考核該控制策略在寬干擾頻域范圍內的適應性也是必要的。另外，傳統減速機構是否能夠滿足該控制方案的使用要求還需進行深入研究。

5 結論

本文針對行進間火炮指向穩定跟蹤問題，提出了基于大地坐標系下采用SINS作為火炮指向角度和調轉角速率反饋的控制策略，并建立了系統模型，進行了穩定和正弦跟蹤仿真驗證，得出如下結論：

1)采用該方法實現了方位和高低兩個穩定系統的獨立控制，二者相互之間不耦合。

2)在大地坐標系下，對火炮指向的穩定跟蹤控制精度優于傳統高炮解算式穩定方式，且響應更快，能夠適應較高的載體姿態擾動幅度和頻率。

3)在火炮行進間且在高射角條件下，純穩定火炮指向的使用條件比既要穩定又要跟蹤火炮指向的使用條件更寬泛，后者對載體行駛或航行舒適性提出了較高要求。

4)采用Lagrange方法所建立的系統動力學模型能夠有效地反映載體、炮塔、火炮之間的運動和動力學耦合關系，仿真運行過程中，模型穩定可靠，對系統控制策略的仿真驗證起到了重要作用。