動力總成質(zhì)心及慣量合成原理研究

宮振興，蘇少博，任爽

（華晨汽車工程研究院底盤集成工程室，遼寧 沈陽 110141）

前言

隨著現(xiàn)代社會的發(fā)展，人們對汽車的使用要求越來越嚴格，近些年尤其體現(xiàn)在整車 NVH及駕駛性上，主機廠則順應市場需求，逐步加強該領(lǐng)域能力的建設(shè)與開發(fā)，其中懸置作為整車重要的零部件之一，對提升整車 NVH及駕駛性起到尤為關(guān)鍵的作用。

懸置的作用是支撐動力總成、限制動力總成運動位移和隔離發(fā)動機振動的作用。懸置在設(shè)計開發(fā)過程中，首選需要對動力總成的質(zhì)量、質(zhì)心及轉(zhuǎn)動慣量進行合成并轉(zhuǎn)換到整車坐標系上。以往在合成轉(zhuǎn)換過程中，通常利用Adams進行仿真計算，但建模工作相對繁瑣，容易疏忽出錯。而本文將公式編輯到Excel中計算，避免Adams建模，節(jié)省時間的同時將出錯率降到最低，最終達到降低計算難度，提升工作效率的目的。

1 輸入測量參數(shù)

合成發(fā)動機和變速器的質(zhì)心及慣量所需測量的參數(shù)如表1。

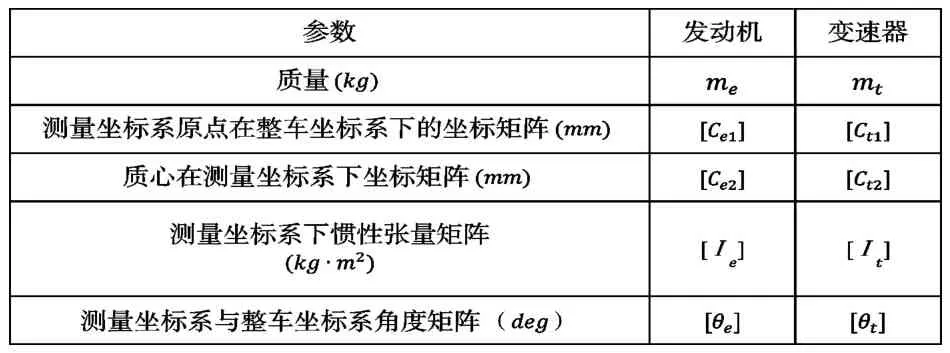
表1 測量參數(shù)

2 質(zhì)心的合成

首先根據(jù)在測量坐標系下測量的質(zhì)心坐標，結(jié)合測量坐標系與整車坐標系的方向關(guān)系，對測量質(zhì)心進行坐標變換，求出整車坐標系下的質(zhì)心坐標，然后再進行質(zhì)心合成。根據(jù)向量空間與基的變換原則可知：

式中：[Ce]為發(fā)動機質(zhì)心在整車坐標系下的坐標矩陣。

變速器質(zhì)心在整車坐標系下的坐標矩陣同理，并記為[Ct]。根據(jù)力矩平衡，可知合成后的動力總成質(zhì)心坐標為：

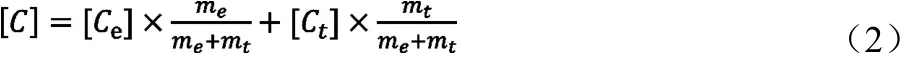
式中：[C]為合成質(zhì)心在整車坐標系下的坐標矩陣。

3 慣量的坐標轉(zhuǎn)換與合成

3.1 慣量的方向轉(zhuǎn)換

方向轉(zhuǎn)換矩陣[θe]定義如下：

其中θexX為發(fā)動機測量坐標系x軸與整車坐標系X軸的夾角，其余同理。測量坐標系下發(fā)動機相對其質(zhì)心的慣性張量矩陣如下：

由式（3）、（4）對慣性張量進行方向轉(zhuǎn)換，公式為：

式中：[IE]為發(fā)動機在整車坐標系下相對質(zhì)心的慣性張量矩陣。

式（5）將發(fā)動機相對質(zhì)心的慣量由測量坐標系方向轉(zhuǎn)換為整車坐標系方向，同理可得整車坐標系下變速器相對質(zhì)心的慣性張量矩陣并記為[IT]。

3.2 慣量的位置轉(zhuǎn)換

發(fā)動機和變速器裝配后，合成質(zhì)心的位置發(fā)生變化，所以還要求出發(fā)動機和變速器相對于合成質(zhì)心的慣量，之后進行慣量合成。

平行軸定理：設(shè)通過剛體質(zhì)心的軸線為Z軸，剛體相對于這個軸線的轉(zhuǎn)動慣量為Jc。如果有另一條軸線 Z’與通過質(zhì)心的軸線Z平行，剛體對通過Z’軸的轉(zhuǎn)動慣量為J=Jc+md2。式中m為剛體的質(zhì)量，d為兩平行軸之間的距離。根據(jù)上述平行軸定理，可以從對于一個以質(zhì)心為原點的坐標系統(tǒng)的慣性張量，轉(zhuǎn)換至另外一個平行的坐標系統(tǒng)。

設(shè)發(fā)動機質(zhì)心與合成質(zhì)心的相對位置

在整車坐標系發(fā)動機相對質(zhì)心的慣性張量

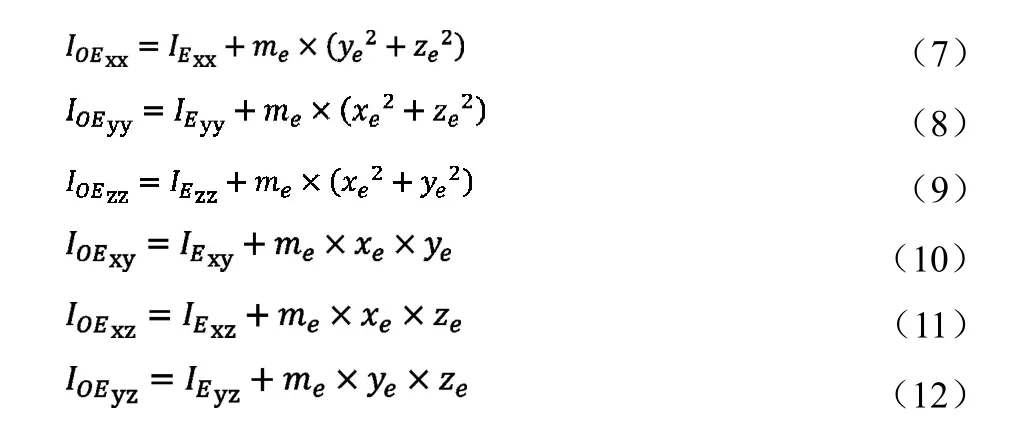
由式（7）～（12），總結(jié)得出公式

式中：[E]為單位矩陣。

同理可求得在整車坐標系變速器相對合成質(zhì)心的慣性張量[TOT]。

3.3 慣量合成

以上求出了發(fā)動機和變速器在整車坐標系相對合成質(zhì)心的慣量，進行相加合成即為動力總成在整車坐標系的慣量，如下

式中：[TPT]為動力總成在整車坐標系下的慣性張量。

4 某車型實例計算及Adams驗證

以某車型動力總成轉(zhuǎn)動慣量為實例，用Excel進行公式編輯和計算，并用Adams/View模塊進行驗證。

4.1 輸入?yún)?shù)

表2、表3列出了合成動力總成質(zhì)心及轉(zhuǎn)動慣量所需測量參數(shù)。

表2 發(fā)動機測量參數(shù)

表3 變速器測量參數(shù)

4.2 計算結(jié)果

通過輸入以上數(shù)據(jù)，輸入到Excel中，得到計算結(jié)果，見表4。

表4 Excel計算結(jié)果

用相同輸入數(shù)據(jù)進行Adams合成計算，結(jié)果見圖1。

圖1 Adams合成計算過程

以上兩組數(shù)據(jù)結(jié)果一致，證明了理論公式的準確性。

5 結(jié)論

本文對動力總成質(zhì)心及轉(zhuǎn)動慣量的合成方法進行了推導，用Excel進行計算并用Adams進行驗證，證明了公式推導的準確性。Excel軟件操作簡單，系統(tǒng)占用資源低，簡化了工作難度，提高了工作效率。