關注課堂教學、改進課堂復習方式

秦小舒

摘 要：當前教育教學改革正在如火如荼進行，新課程教學理念已經深入到教學中。教師需探索如何激發學生學習興趣、優化課堂教學等方面。尤其是復習課，科學有效的組織復習，可以把各知識點前后串聯，提高學生解題能力。要在短時間內使學生通過復習初中數學的所有概念，提高解題技巧，就需要教師關注課堂教學、改進課堂復習方式。

關鍵詞：圓;動態;課堂復習方式

中圖分類號：G633.5? ??文獻標識碼：A

一、主題與背景

《圓》的內容在滬教版九年級數學第二學期第二十七章。雖然學生已經學習了圓的相關知識，但在整理和復習的方法上比較薄弱。上這節課的目的之一也是對已學知識查漏補缺，二是提高學生的得分率。結合這兩點，我確定了本節課的主題：“圓的專題復習——與圓有關的動態問題”。

二、課例研究過程

1.前期準備

自己獨立備課。思考了復習課的主題“圓中動點問題的相關計算”。教學目標：圓的分類討論問題。分別選取了三個不同動態問題：點動、線動、面動。只考慮了圓中的三種位置關系。對于這堂課的理解只停留在表面上，教學目標不夠準確，對知識點的歸納整理也不夠具體。

通過備課組內交流，發現：我對課堂練習的選取上存在不足，不能準確把握中考方向，練習沒有典型性。通過反復地修改，理出了一條主線——在平面直角坐標系這個大背景下，由x軸上的一個動點，動圓的平移帶來了點與圓、直線與圓、圓與圓的關系。慢慢升華到綜合題，分別由x軸、平行于x軸上的兩個動點，引出與圓有關的函數關系式、兩圓的關系等。

2.課堂教學

我開始第一輪上課，在課堂中，我發現給學生基礎題思考的時間太長，導致后面綜合題的思考時間太短。出題意圖是希望學生能夠獨立完成圓中求弦的長，并能夠書寫完整，以及掌握在一個圓中做輔助線的方法：做半徑或者做弦心距，構造直角三角形解題。幾何題的書寫嚴謹性非常重要，但是大部分學生浪費了很多時間在書寫上，也因此課堂的學習氣氛也比較沉悶。

第二輪，我縮短了在基礎題上花費的時間，將側重點放在了綜合題上。帶來的新的問題是：在用x的代數式表示圓P的半徑時，學生花了很長時間在這個代數式上，不會另設圓P的半徑為y，那么轉為求x、y的函數關系式。然而x的取值范圍是這節課的一大難點，學生不理解、教師沒講透。

第三輪中，把求代數式的問題改成求y關于x的函數解析式，降低了難度。在課堂中如何求函數解析式的問題，也做了及時的知識梳理：通過構造直角三角形用勾股定理求解，或者構造相似三角形用對應邊比求解。著重講解了定義域問題。通過猜測、直觀觀察、畫兩種臨界情況下的圖形、計算來確定定義域。其實能夠畫出圖形那么定義域問題也就解決了。所以這堂課的一個重點是：學生根據問題的條件和結論畫出圖形。

以下是第三輪中的課堂實錄片斷：

已知：在平面直角坐標系xOy中，點A（10，0）、點B（0，5），以A、O、B、D為頂點的四邊形為矩形，點P是x軸正半軸上的一個動點，點Q是邊BD上的一個動點。以點P為圓心作圓，⊙P經過點O和點Q，連接OQ、PQ。

當點P在邊OA上時，設BQ=x，OP=y，求y關于x的函數解析式，并寫出x的取值范圍;

（請學生讀題）

（學生獨立完成第一小題，學生上臺畫輔助線方法）

師：為什么想到這樣做一條輔

助線？

生：因為OQ是一條弦，點P是圓心，所以垂徑定理。

師：因為圓我們想到作弦心距，因為弦心距，我們想到又構造直角三角形。這么作的好處？

（學生標出已知條件）

生：可以求出OQ。

師：也就知道了OQ的一半。那么可以借助這個角的？

生：余弦值。

師：既然這個角的余弦值有了，那么這個關系式是？

（展示另一種方法）

生：首先告訴我們是一個矩形，想到了作一個垂直以后，這里又是一個矩形。BQ這一段就等于這一段，做了垂直以后構造了一個直角三角形，這段是5，等于這一段，這一段都是圓的半徑，所以等于OP，就是y。然后可以利用勾股定理，把MP求出來。得y2=（y-x）2+52。

師歸納：在解函數關系式時，通常用的兩種方法：一是找相等的角，運用相似三角形或銳角三角比構造函數關系式。也可以通過勾股定理來構造函數關系式。

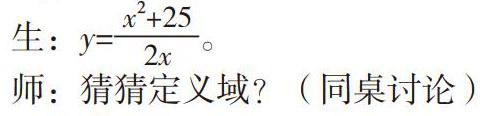
生：0<x≤10

師：到底是不是呢？

（展示幾何畫板中，動態移動）

師：x=10可以嗎？

全班：可以。

師：那x的范圍確定了，等于10是可以的。那是大于0嗎？等于0是不可以，為什么？因為⊙P是經過了O、Q，也就是點P在線段OQ的垂直平分線上，又P在x軸上，所以有沒有交點？

全班：沒有。

師：等于0不可以。只要大于0咯？這樣可以嗎？

生：不可以。

師：為什么？

生：因為點P在邊OA上。

師：又是題目給的。所以我們審題要清。當點P在邊OA上時。那既然Q不能確定，那我們可以確定誰？

全班：OP。

師：就是點P的位置可以確定。當點P怎么樣時？

全班：與A重合。

師：此時這段QB最？

全班：最小。

師：也就是x最小。此時是多少？

生：y=10。

三、課例研究的成效與反思

在這過程中，大部分學生積極參與學習中，并能在熟練掌握圓的知識的前提下解決相關問題，知道解動態問題的一般方法，明白可以將圓的知識轉化成基本圖形的知識，能比較好地達到教學目標。學生對《圓》的知識有了新的理解，在后續的練習中，學生在圓中添輔助線幫助解題的能力明顯提升了。有了解題技巧，就不怕復雜的圖形了。

本堂課最遺憾的是綜合題的最后一小問沒有來得及完成。有遺憾才能化成動力，更好地思考與反思。或許在上課開始時，可以省略對《圓》知識點的梳理，那么多了的時間可以留給學生們完成最后一小問。

四、結語

總之，復習課是幫助學生查漏補缺、系統整理的有效途徑。教師需要關注課堂教學，改進課堂復習方式，讓復習課成為真正高效的課堂。當高效的復習課成為我們的課堂常態，教學質量就會更上一層樓。

參考文獻：

[1]林曉剛.淺談與圓有關的計算與證明的專題復習[J].讀與寫（教育教學刊），2011（6）.

[2]王曉東.高三復習課中的“課題研究式”教學[J].中國數學教育，2010（12）.