FA-PMA-VMD方法及其在齒根裂紋故障診斷中的應用

程軍圣, 李夢君, 歐龍輝, 楊 宇

(湖南大學 汽車車身先進設計制造國家重點實驗室，長沙 410082)

齒輪作為旋轉機械中不可或缺的一部分，其故障信號往往表現出非線性非平穩特性，針對這種非線性非平穩特性，常采用時頻分析方法對這類信號進行預處理。常用的時頻分析方法有經驗模態分解(Empirical Mode Decomposition, EMD)等方法[1-3]。但是EMD方法是基于“經驗性”算法，缺少堅實的數學基礎[4]，并且存在模態混淆等缺陷[5]。Dragomiretskiy等[6]最近提出了一種新的分解方法—變分模態分解(Variational Mode Decomposition，VMD)。它是一種具有堅實的數學基礎的分解方法，通過建立對應的約束變分模型表達式，引入二次懲罰因子和拉格朗日乘法算子，將約束性變分問題變為非約束性變分問題，最終獲得具有數學意義并且能有效抑制模態混疊現象的帶限內稟模態函數。

VMD相比EMD等方法，在很多方面表現出更加優異的性能[5-9]。Zheng等將VMD方法應用在碰撞信號的去噪上，效果明顯優于EMD方法，文獻[7]論證了VMD方法有很好的濾波特性，文獻[8]等將VMD方法應用到旋轉機械的碰摩故障診斷，唐貴基等將VMD方法應用到軸承的早期故障診斷。但是VMD方法自身也存在著一些缺陷。首先，在用VMD方法分解信號之前，必須預先設定模態數和懲罰參數，文獻[7]將去趨勢波動分析(Detrended Fluctuation Analysis，DFA)方法與VMD方法相結合，建立光纖陀螺信號的長相關系數α0與模態數k的關系式，以計算α0獲得最佳的模態數，但是忽略了懲罰參數α對對于VMD分解效果的影響，且僅應用于光纖陀螺信號。文獻[8]雖然考慮了懲罰參數α對于VMD分解效果的影響，但是只能將VMD算法運用到簡單的諧波信號和噪聲的合成信號。其次，在用VMD方法對信號分解后，進行濾波或提取特征值等不同處理時，需要選擇合適的分量和排序，但是VMD方法存在分解出來的分量排列不規律的缺陷，從而給分量的選擇和排序帶來困難。

針對上述缺陷，本文首先把主模態分析(Principle Mode Analysis,PMA)與VMD方法結合，使帶限內稟模態函數(Band-Limited Intrinsic Mode Function, BIMF)分量按照一定的規則排序。然后用螢火蟲算法對變分模態分解方法的最佳影響參數[k,α]組合進行搜索，并提出一個新的特征值—正交低峰值作為螢火蟲算法優化[k,α]的目標。搜索得到的最佳結果設定變分模態分解算法的懲罰參數α和分量個數k，并根據PMA處理預先設定的故障特征參數綜合特征將BIMF分量進行排序。最后，用復雜調幅調頻仿真信號對FA-PMA-VMD方法進行仿真分析，并將FA-PMA-VMD方法運用到實際齒根裂紋故障診斷中，驗證改進VMD方法的實際有效性。

1 FA-PMA-VMD方法

1.1 PMA-VMD方法

式(1)信號其時域波形如圖1所示，由中心頻率分別為200 Hz,400 Hz,20 Hz三個分量合成。

(1)

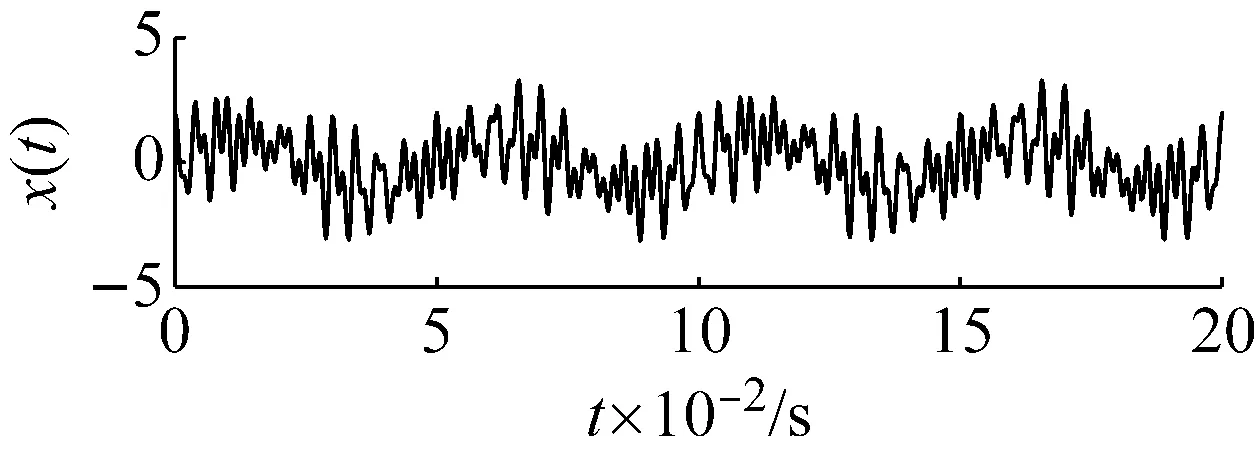
圖1 輸入信號的時域波形圖

直接用VMD分解后各個BIMF分量及其頻譜圖，如圖2和圖3所示，可觀察到，這些BIMF分量并沒有按照中心頻率高低的順序這類的規律排列。

當實際信號的BIMF分量較多，對于多個排列無規律的BIMF分量，需要重點研究信號的一個或多個特征時，無法直接判斷哪一個BIMF分量的綜合特征最明顯，也無法直接判斷中心頻率大小相鄰的幾個BIMF分量之間的關系。因此需要一種針對特征參數分析的方法對VMD方法分解的BIMF進行分析處理。本文引入PMA方法對VMD方法分解的分量進行排序。PMA是受主分量分析啟發，根據故障特征參數，把主模態用于振動信號BIMF分量分析的方法。

本文把某種故障特征最明顯的BIMF分量稱為主模態分量，主模態分量對應的模態稱為主模態。PMA方法為：

步驟1故障信號X(t)經過信號分解后為個n個BIMF與余量res之和即

(2)

步驟2提取第k個BIMF的n種故障特征參數MK1,MK2,MK3,…,MKn,將這些故障參數組成一個故障特征參數向量FK=[MK1,MK2,MK3,…,MKn](k=1,…,n)。FK可以組成一個故障特征參數矩陣F

F=(F1,F2,F3,…,FN)T

(3)

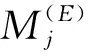
m=(1,2,…,n)

(4)

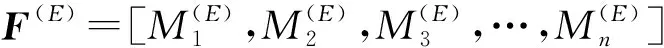
m=(1,2,…,n)

(5)

步驟5式(5)可以看到協方差矩陣L為方陣，求解L的特征值λ與特征向量v

Lv=λv

(6)

步驟6將特征值按大小排列λ1≥λ2≥…≥λn,每個特征值λk的單位化的特征向量組成的空間V

V=(v1,v2,…,vn)T

(7)

步驟7F(E)到空間V的投影表示為S(S=(s1,s2,…,sn)T)。

(8)

步驟8計算各sk對應的故障特征參數列的投影和Bk

(9)

步驟9按照投影絕對和Bk的大小順序，把Bk對應的BIMF分量進行排序，得到對一個信號的BIMF分量進行主分量分析的結果。

含(E)表示單位化后的變量，故障特征參數矩陣通過步驟3～步驟6的變換，消除了各個特征參數向量的相關性，并得到了一組故障特征參數矩陣的單位正交基，保證在步驟7中的單位化故障特征參數投影信息獨立性，步驟8以投影和的方式評判綜合信息量的大小。第k個BIMF分量對應的特征參數向量在空間V中的投影和sk越大，說明該BIMF所包含的綜合故障信息量越大，其對應的模態對故障越敏感。

PMA-VMD方法是通過VMD將輸入信號分解后，把PMA用于對BIMF的分析的方法。具體步驟如下：首先通過VMD方法對信號進行分解，得到BIMF分量；其次提取各BIMF分量的故障特征參數，得到故障特征參數向量；然后用PMA對故障特征參數進行分析，得到綜合故障特征的大小順序；最后按照故障特征的大小順序對BIMF重新排序。

通過上面分析可以發現，PMA-VMD方法對故障特征參數綜合排序，以達到分解出的BIMF分量按照所選的故障特征參數綜合特征從強到弱排列。

本文此處以頻率重心為特征參數，模態的個數k依據仿真信號的情況設置為3，懲罰參數α設置為1 200。

利用PMA-VMD對于式(1)對應的輸入信號分解后的結果如圖4所示。對比圖4與圖2，圖3，可以發現用PMA-VMD對輸入信號進行分解后BIMF分量按照中心頻率的大小，從小到大排列。

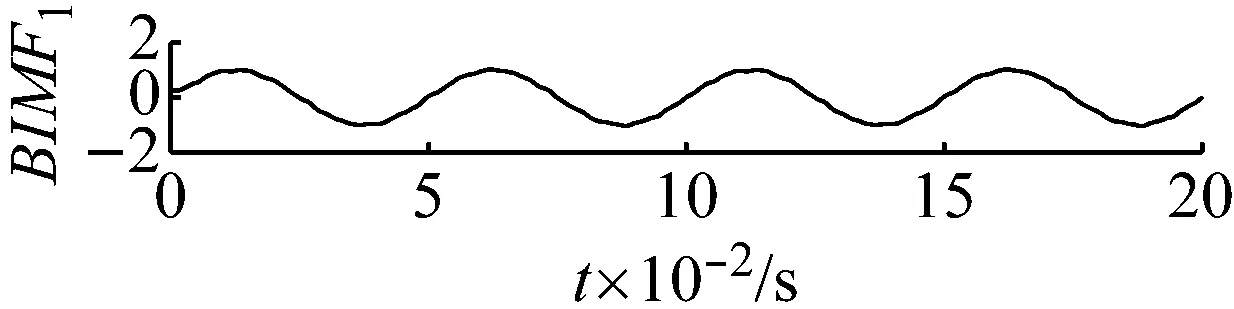
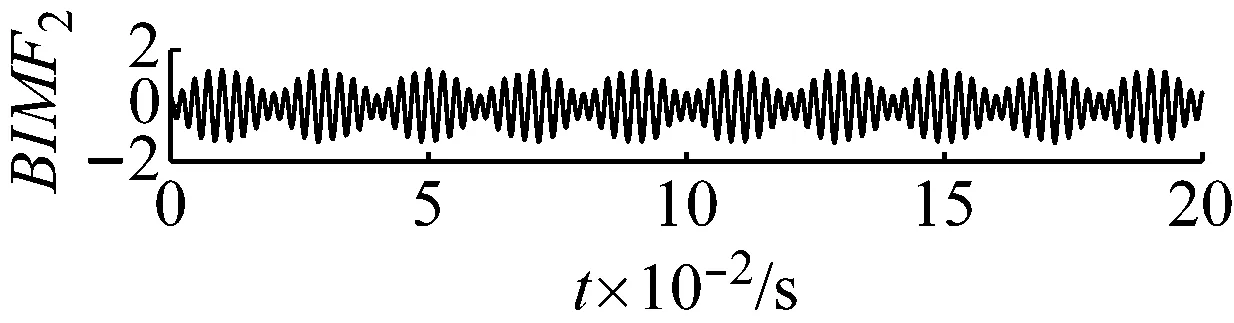
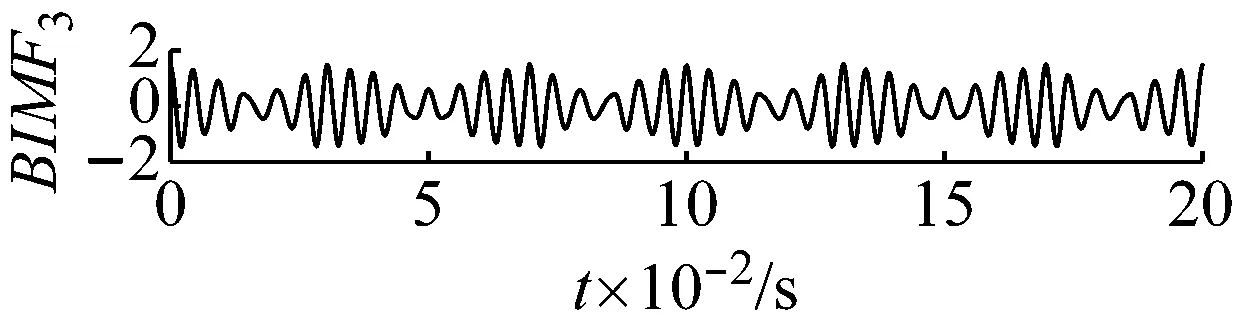
圖2 各個分量的時域波形圖

Fig.2 The time domain waveform of each BIMF signal

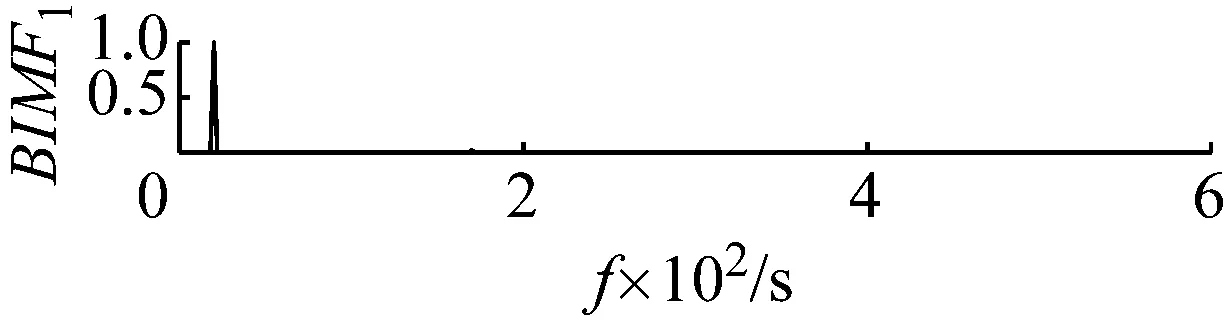
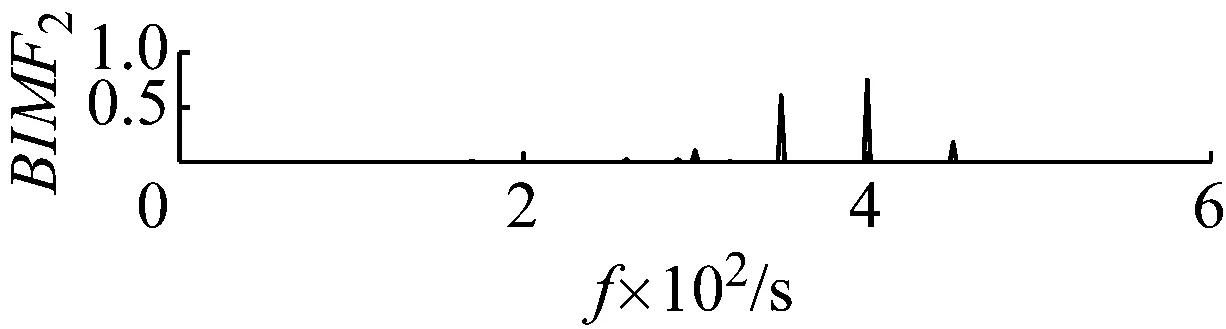
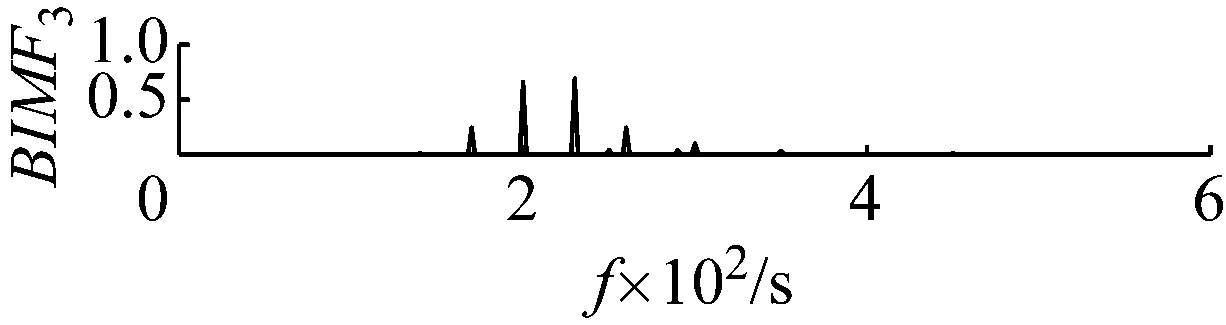
圖3 各個分量的頻譜

Fig.3 The frequency spectrum of each BIMF signal

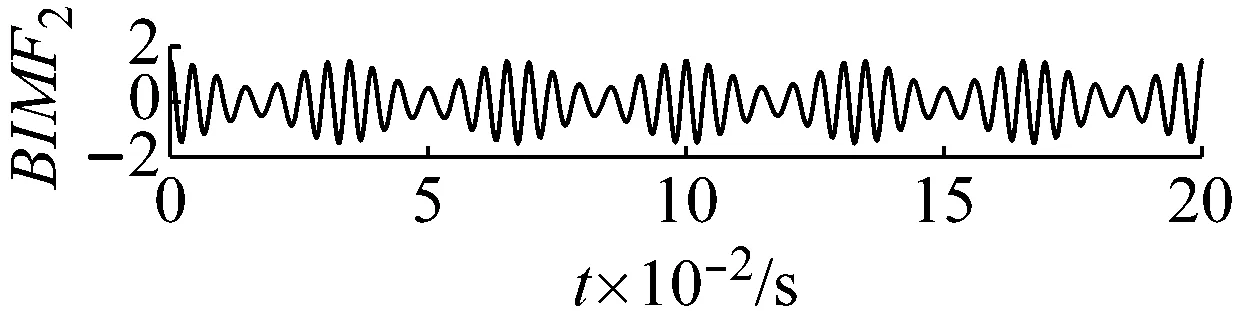
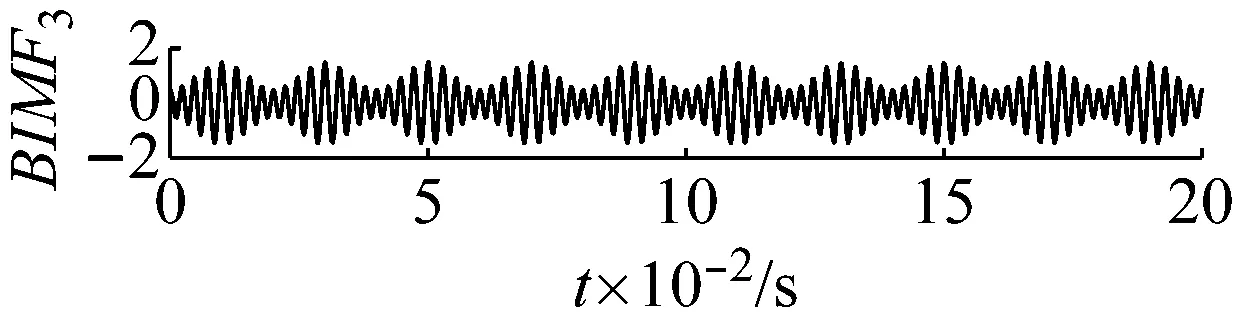
圖4 各個分量的時域波形圖

Fig.4 The time domain waveform of each BIMF signal

1.2 FA-PMA-VMD方法

VMD在對信號分解前，要給出模態的個數，和懲罰參數，即人為設定k的值和α值。根據上文可以知道，模態個數選取的多少會直接影響最終的分離結果。

本文以式(1)為輸入信號，來試驗不同[k,α]參數的選取對于VMD算法的分解效果的影響。

當k值取4，同時取一個極大的懲罰參數值α=3×106。此時中心頻率為200 Hz的調幅調頻信號完全被舍棄,如圖5和圖6所示。

當k值取4，同時取一個較小的懲罰參數值α=300，此時三個中心頻率為20 Hz,200 Hz和400 Hz都存在三個BIMF分量中，但是中心頻率為200 Hz的調幅調頻信號被分到了BIMF2,BIMF3兩分量中，如圖7和圖8所示。

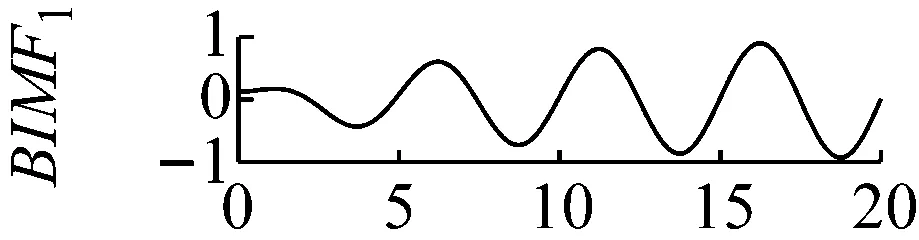
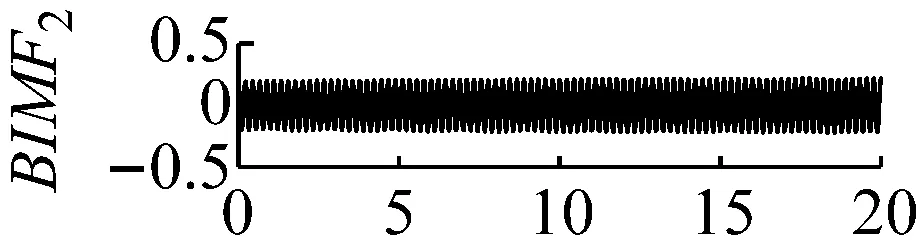
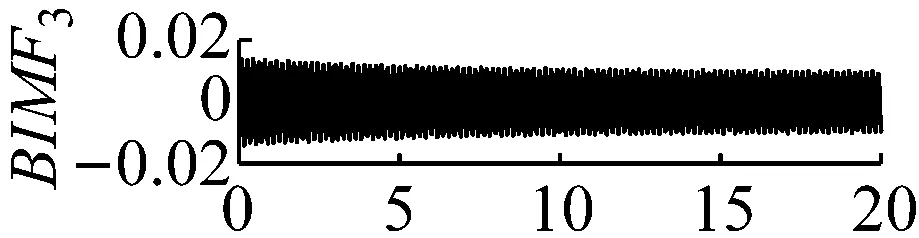
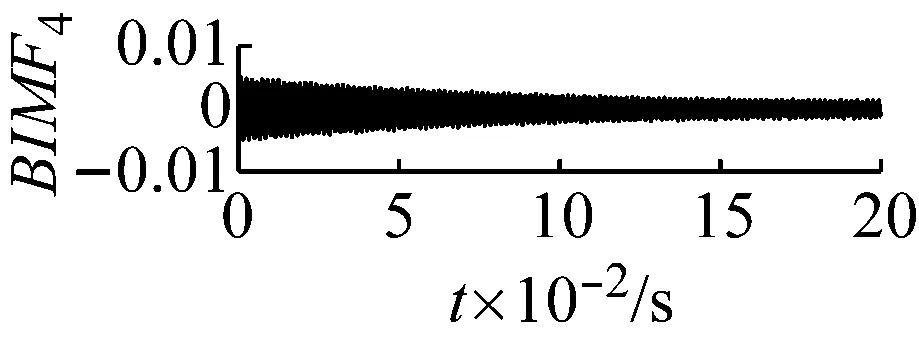
圖5k=4,α=3×106時域波形圖

Fig.5 The time domain waveform of each BIMF signalk=4,α=3×106

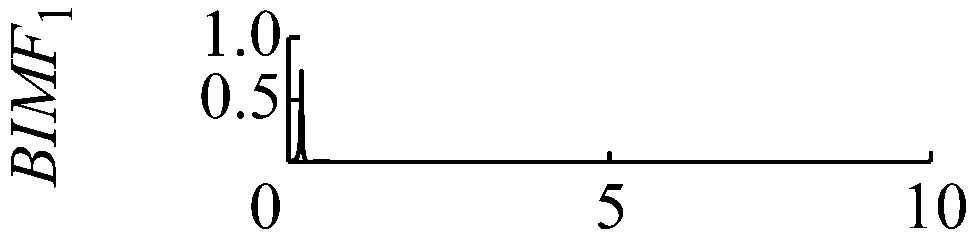
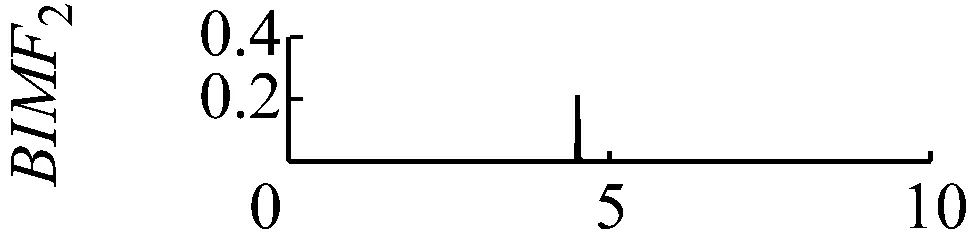
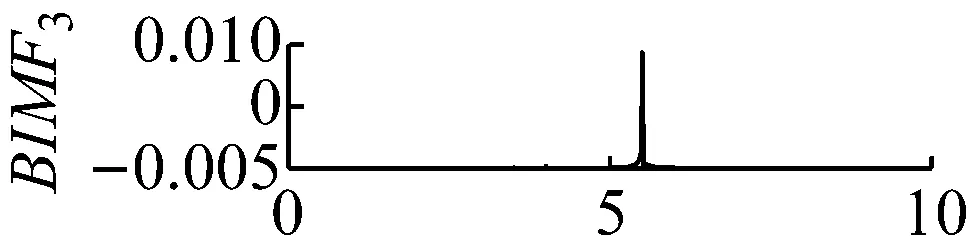
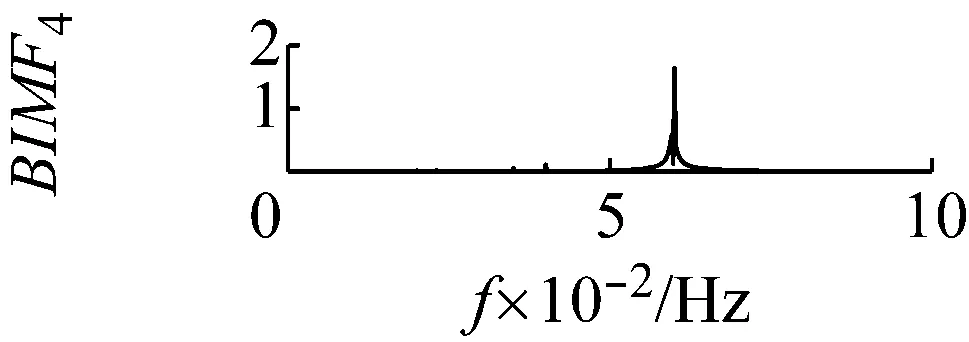
圖6 k=4,α=3×106頻譜

Fig.6 The frequency spectra of each BIMF signalk=4,α=3×106

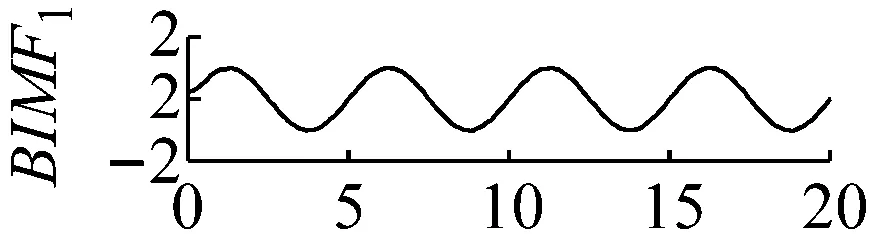
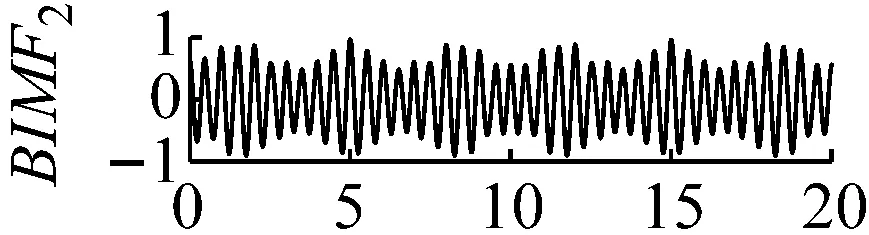
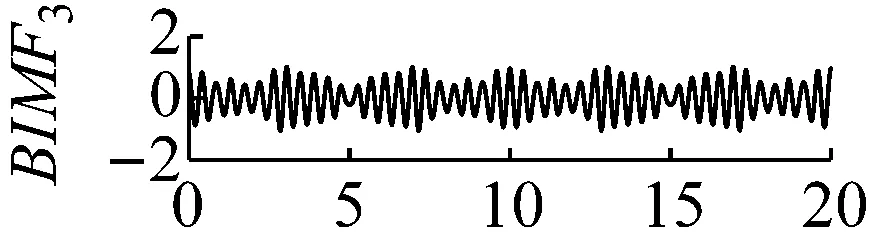
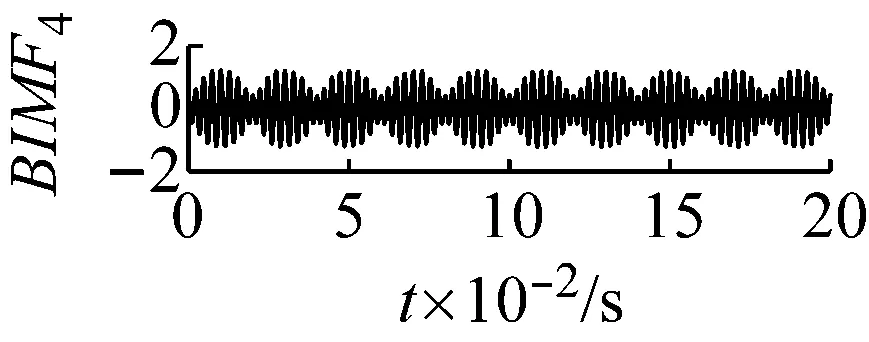
圖7k=4,α=300時域波形圖

Fig.7 The time domain waveform of each BIMF signalk=4,α=300

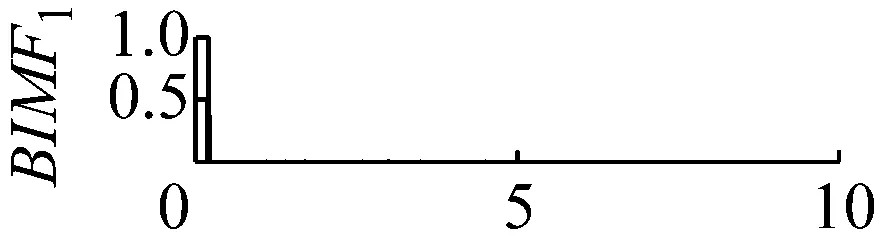
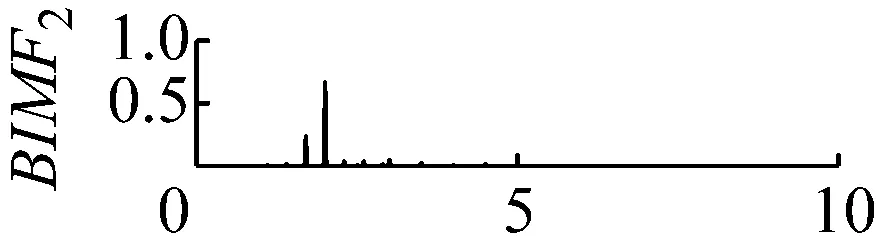
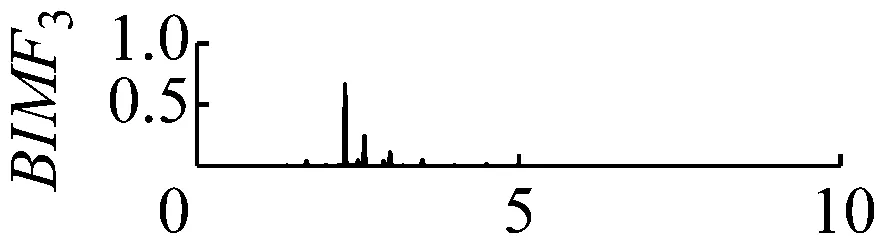
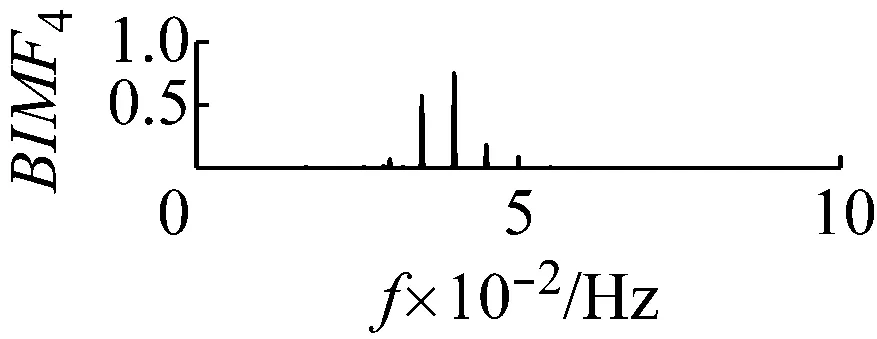
圖8 k=4，α=300頻譜

Fig.8 The frequency spectra of each BIMF signalk=4，α=300

由于k值和α的選取對于故障的提取至關重要。而對一個參數單獨優化往往會忽略這兩個參數之間的相互影響，只能獲得相對最優的結果。因此，本文引入螢火蟲算法對兩個影響參數同時進行優化，以避免人為主觀因素的干預，自動篩選出最佳的影響參數組合。

利用螢火蟲算法搜尋VMD算法的模態數和懲罰參數α時，需要一個評價參數來評價螢火蟲每次更新位置的適應度。本文引入正交低峰值作為優化目標，正交低峰值是一個新的評價參數，其計算如式(10)所示，式(10)中k為分量的個數，m為螢火蟲的個數。

正交低峰值的計算條件是BIMFi,BIMFi+1為中心頻率相鄰的兩個BIMF分量。

(10)

I=Zm=F(k,α)

(11)

β(r)=β0e-γrm

(12)

式中:k為分量的個數，α為懲罰參數，這兩個參數作為函數的輸入變量，分別為螢火蟲算法中的x軸和y軸上的變量;I為函數的輸出變量，為螢火蟲算法中z軸的變量。其計算原理如圖9所示。

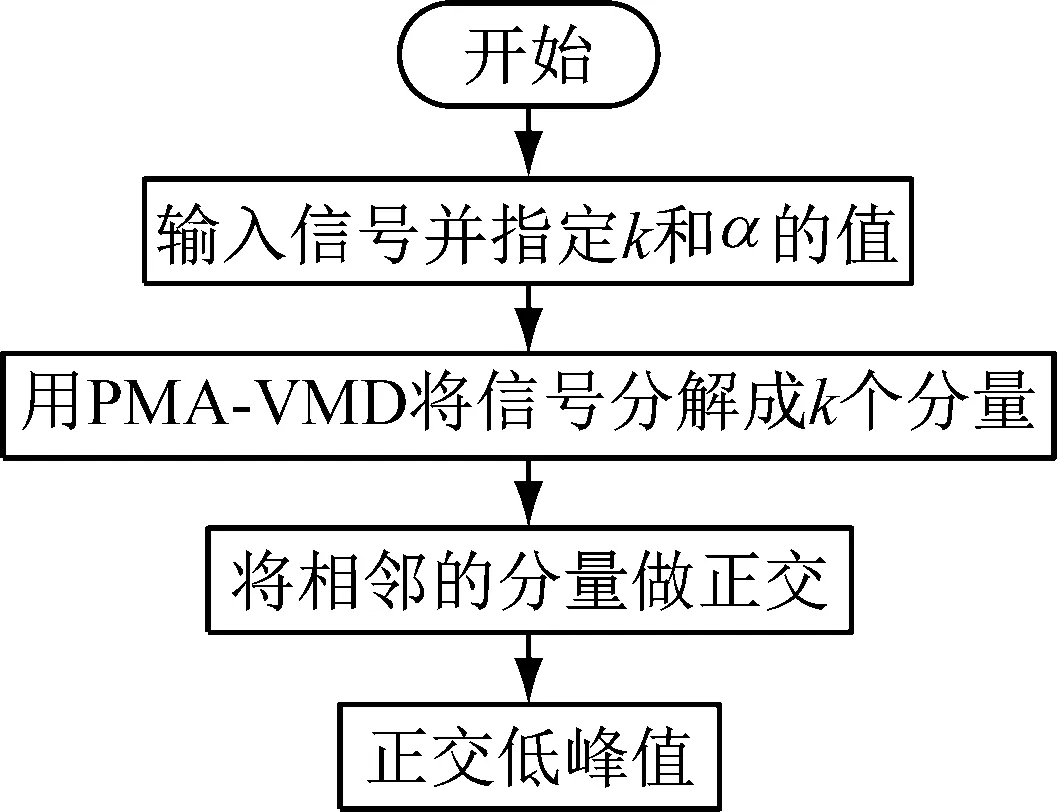
圖9 目標函數計算原理圖

式(10)和式(11)對目標函數的定義可知，在用螢火蟲算法搜尋VMD算法的模態數k和懲罰參數α時，首先需要以頻率重心為特征參數，通過PMA對BIMF分量按照中心頻率的大小，從小到大排列，以便求出對應分量的個數和懲罰參數的目標函數I。

FA-PMA-VMD算法的計算步驟為：

步驟1設置故障特征參數(頻率重心為默認設置，用于計算螢火蟲目標函數前通過PMA對獲得的BIMF分量進行排序。其他故障特征參數根據實際的故障來設置)。

步驟2初始化螢火蟲算法參數，最大吸引力β0、光吸收系數γ、步長因子α，給定群體規模m，指定迭代次數T。

步驟3隨機初始化螢火蟲的位置，計算螢火蟲的目標函數I=Zm=F(k,α)作為各自最大熒光亮度In。

步驟4計算螢火蟲的相對亮度和吸引度β[10]，吸引度公式如式(12)所示，根據相對亮度決定螢火蟲的移動。

步驟5更新螢火蟲的空間位置，對處于最佳位置的螢火蟲進行隨機擾動。

步驟6根據螢火蟲的位置從新計算螢火蟲的亮度。

步驟7判斷是否滿足終止條件，如果滿足，跳出循環獲得最優的全局極值點Zm和個體[k,α]。如不滿足，則重復步驟3～步驟5直到滿足循環終止條件。

步驟8根據前面確定的[k,α]，確定BIMF最終分量的個數，最后通過PMA獲得按照所選的故障特征參數綜合特征從強到弱排列BIMF分量。

2 仿真信號分析

在式(1)的信號中加入一個正弦信號n(t)=sin(2π120t)，如式(13)所示，作為輸入信號,如圖10所示。

S(t)=X(t)+n(t)

(13)

對輸入信號S(t)用EEMD進行分解，對于幅值系數K和總體平均次數M的選取，Wu等[11]建議K由原信號的標準差乘以一個分數來定義， 一般取原信號標準差的0.2倍。這樣當M為一、兩百次的時候，殘留噪聲引起的誤差一般會處在一個比較低的水平(不足1%)。同時，他們還認為：在噪聲水平合適的條件下，一味地增加執行次數對結果的改善并不顯著。而反過來在一定范圍內提高噪聲水平對結果的影響也甚微，當然噪聲太大也可能完全淹沒信號的本質特征，使得分解毫無意義。本文中K取原信號標準差的0.2倍，M取值為100。

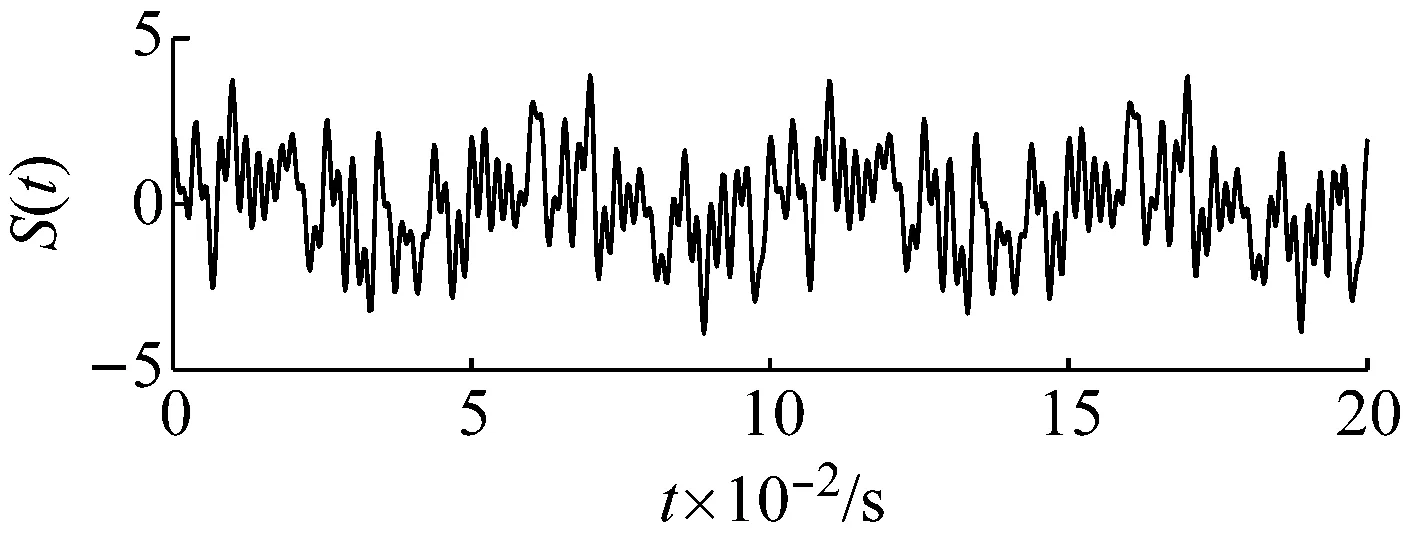
圖10 加入諧波信號后的時域波形圖

其結果如圖11所示。可以發現分量之間出現了較為嚴重的頻率混疊現象。

用FA-PMA-VMD方法對輸入信號進行處理，首先初始化螢火蟲算法的相關參數如表1所示。表1中：β0為最大吸引力;γ為光吸收系數;α為步長因子;n為群體的規模;T為迭代的次數。

表1 螢火蟲算法的相關參數

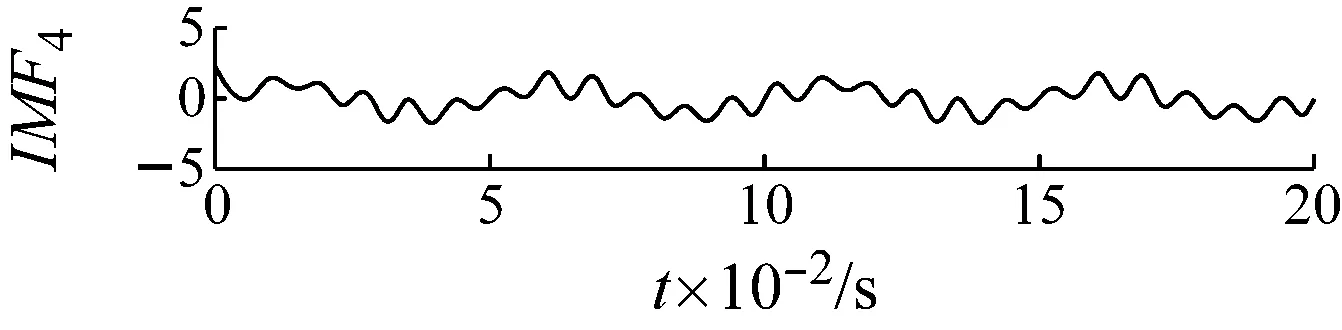
圖11 EEMD分解時域波形圖

齒輪齒根裂紋故障會對齒輪的信號帶來沖擊，文獻[12]表明峭度(Kurtosis，Kurt)對于沖擊信號特別敏感，而均方根值(Root Mean Square，RMS) 能表明信號的強弱，多尺度模糊熵(Multiscale Fuzzy Entropy,MFE)為信號復雜度的量化統計指標[13]，因此都對齒根裂紋故障比較敏感。齒根裂紋故障信號為調幅調頻信號，故本文將Kurt,RMS和MFE為故障特征參數。

按照FA-PMA-VMD方法的計算步驟，經過計算可以得到全局極點min(Imax)=0.009 2和最優個體值[k,α]=[4,2 325],計算結果如圖12所示。多次計算后的結果如表2所示。

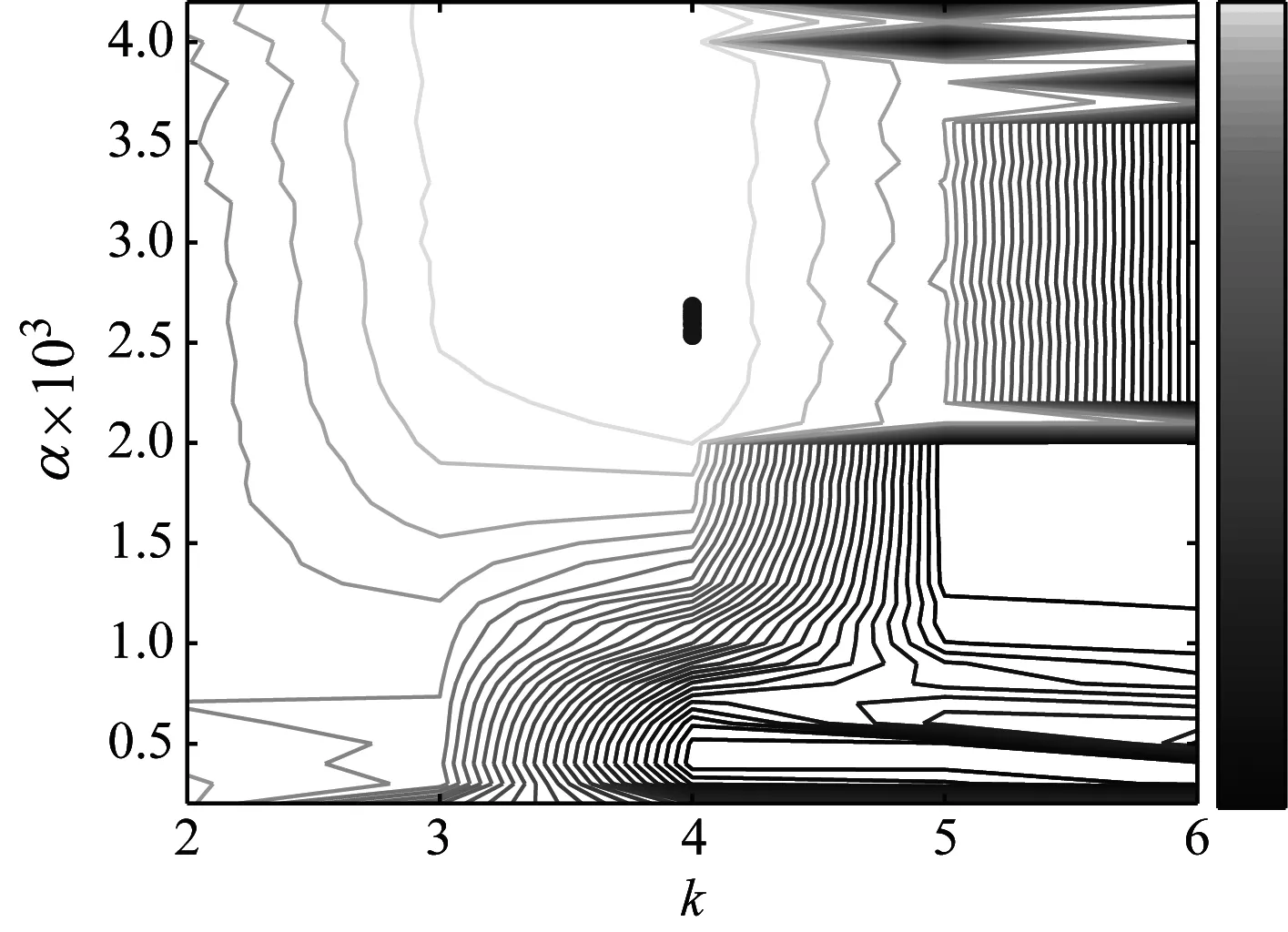
圖12 螢火蟲算法對k和α優化后結果

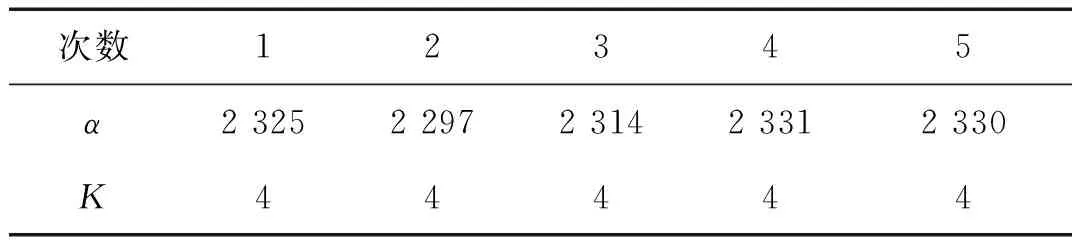
次數12345α2 3252 2972 3142 3312 330K44444

取五次計算后的平均值[4,2 319.4]作為優化后的最終結果，FA-PMA-VMD分解的最終分量的故障特征參數列的投影和Bk如表3所示。其分解結果如圖13和圖14所示。

對比圖11和圖13、圖14，可以觀察到FA-PMA-VMD對仿真信號的分解后，在效果優于EEMD，同時也可以觀察到EEMD分解后的分量只是由能量的大小按照高頻到低頻排列，而FA-PMA-VMD分解后，將含有豐富故障特征的調幅調頻信息的BIMF分量排在前面。

表3最終分量的故障特征參數列的投影和Bk值

Tab.3Bkvaluesofthefaultcharacteristicparametersofthefinalcomponent

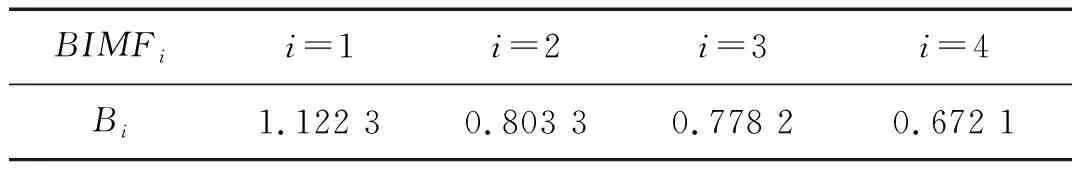
BIMFii=1i=2i=3i=4Bi1.122 30.803 30.778 20.672 1

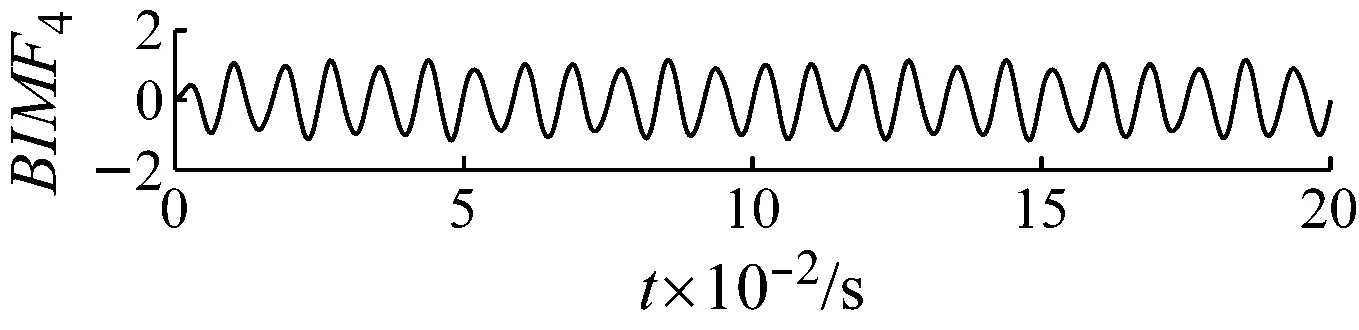
圖13 FA-PMA-VMD分解分量時域波形圖

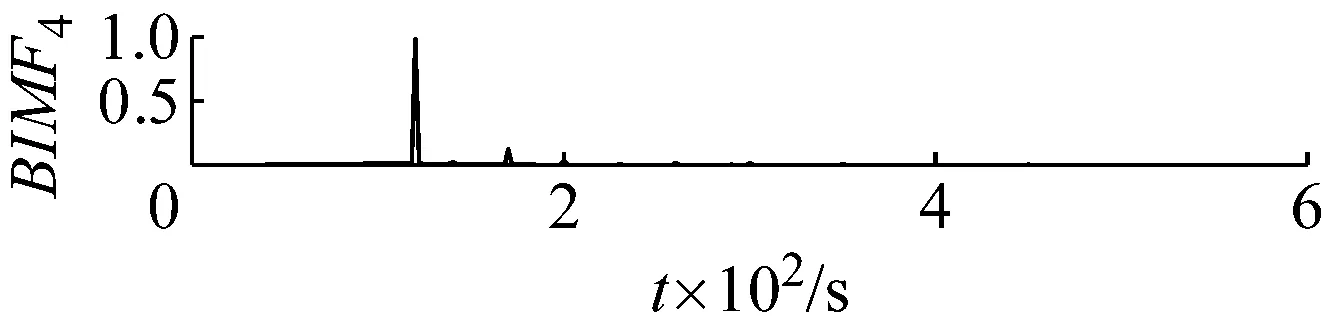
圖14 FA-PMA-VMD分解分量頻譜

Fig.14 Frequency spectra of the results decomposed by FA-PMA-VMD

3 實驗信號分析

為驗證本文方法對于振動信號分析的有效性，利用實際含有齒根裂紋的齒輪振動信號進行驗證。

實驗中齒輪為模數2.5 mm、齒數37的標準齒輪，齒根切割的裂紋寬度為0.15 mm，深度為20%。實驗伺服電機主軸轉速為 600 r/min，即轉頻為fr=10 Hz,嚙合頻率fz=370 Hz。實驗采樣頻率為1 024 Hz，每次采樣時間持續1 s。采集到的實驗信號如圖15所示。

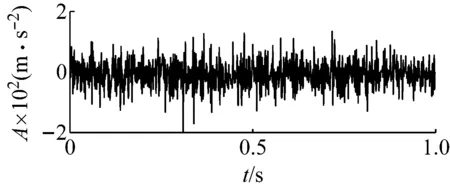
圖15 齒輪裂紋故障下的實驗信號

用FA-PMA-VMD方法對實驗信號進行分解，根據第2節仿真信號分析，選取RMS,Kurt,MFE為故障特征參數。最終分量的個數以及對應分量的故障特征參數列的投影和Bk如表4所示。分解結果如圖16和圖17所示。繼續對BIMF2分量進行包絡解調運算，并作出其包絡譜如圖18所示，其中特征頻率及倍頻處譜線幅值十分突出，說明特征頻率信息被提取了出來并包含在BIMF2分量中。

表4最終分量的故障特征參數列的投影和Bk值

Tab.4Bkvaluesofthefaultcharacteristicparametersofthefinalcomponent

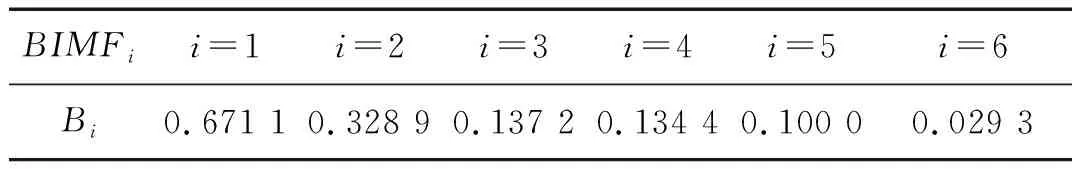
BIMFii=1i=2i=3i=4i=5i=6Bi0.671 10.328 90.137 20.134 40.100 00.029 3

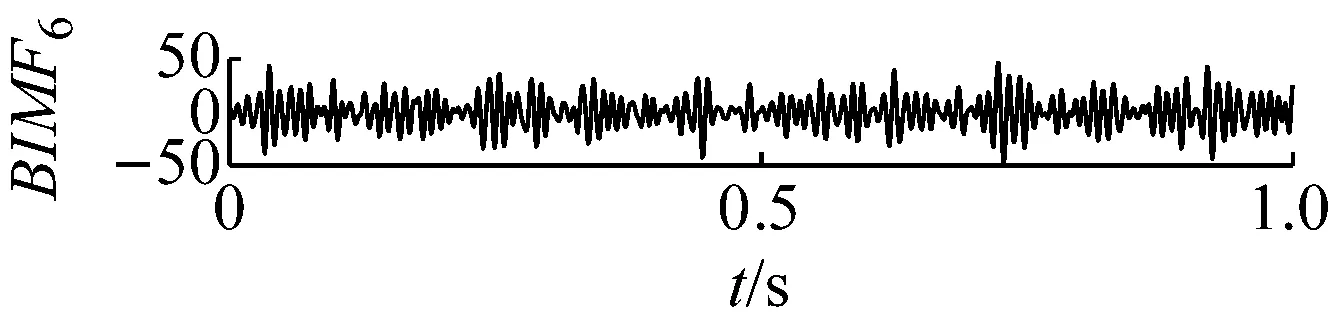
圖16 BIMF分量的時域波形圖

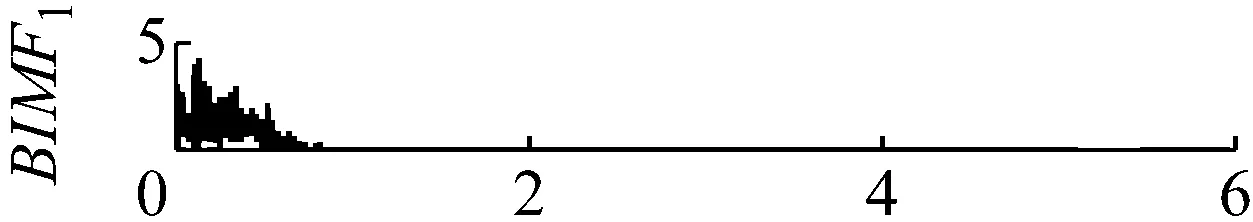
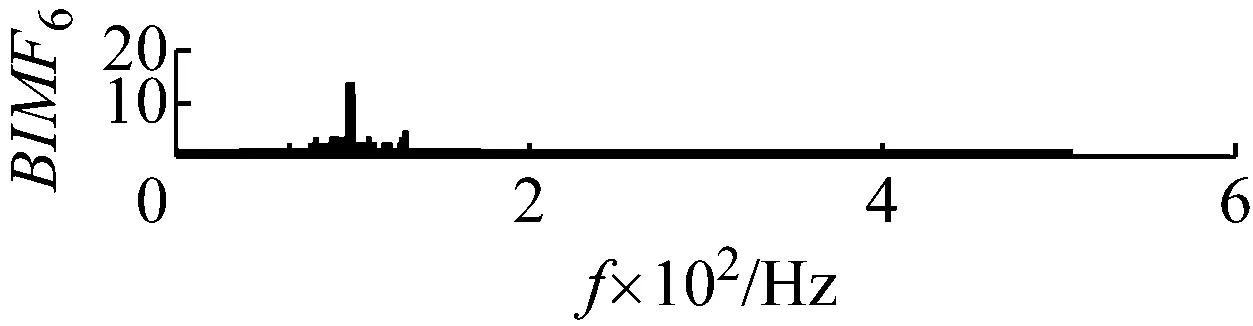
圖17 BIMF分量的頻譜

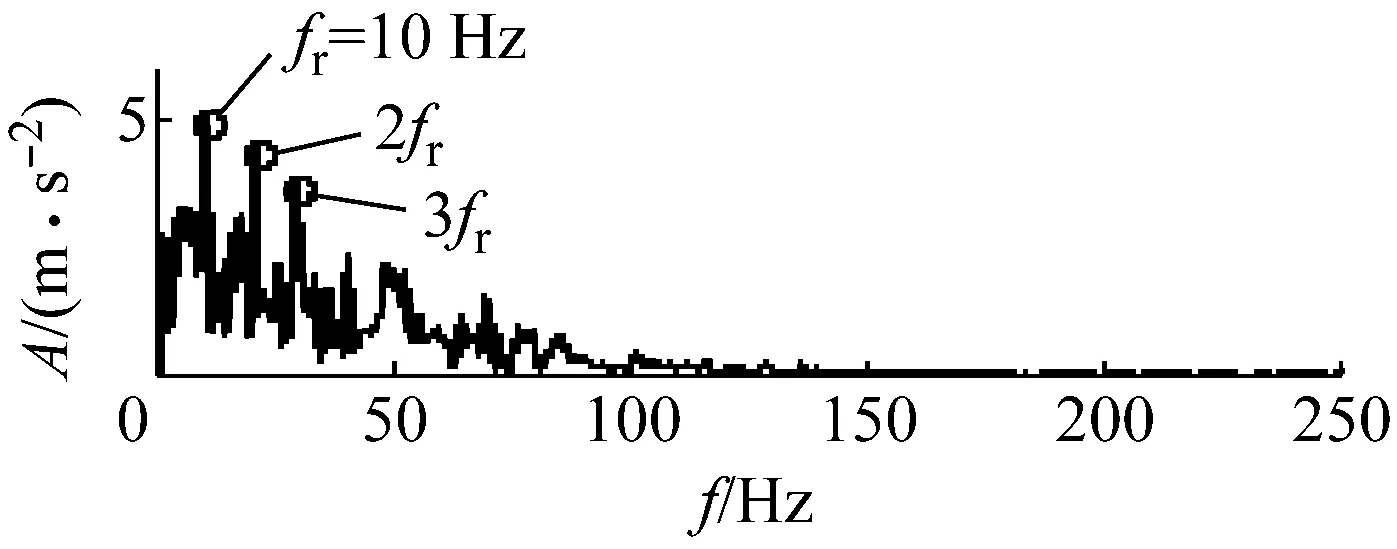
圖18 BIMF2分量的包絡譜

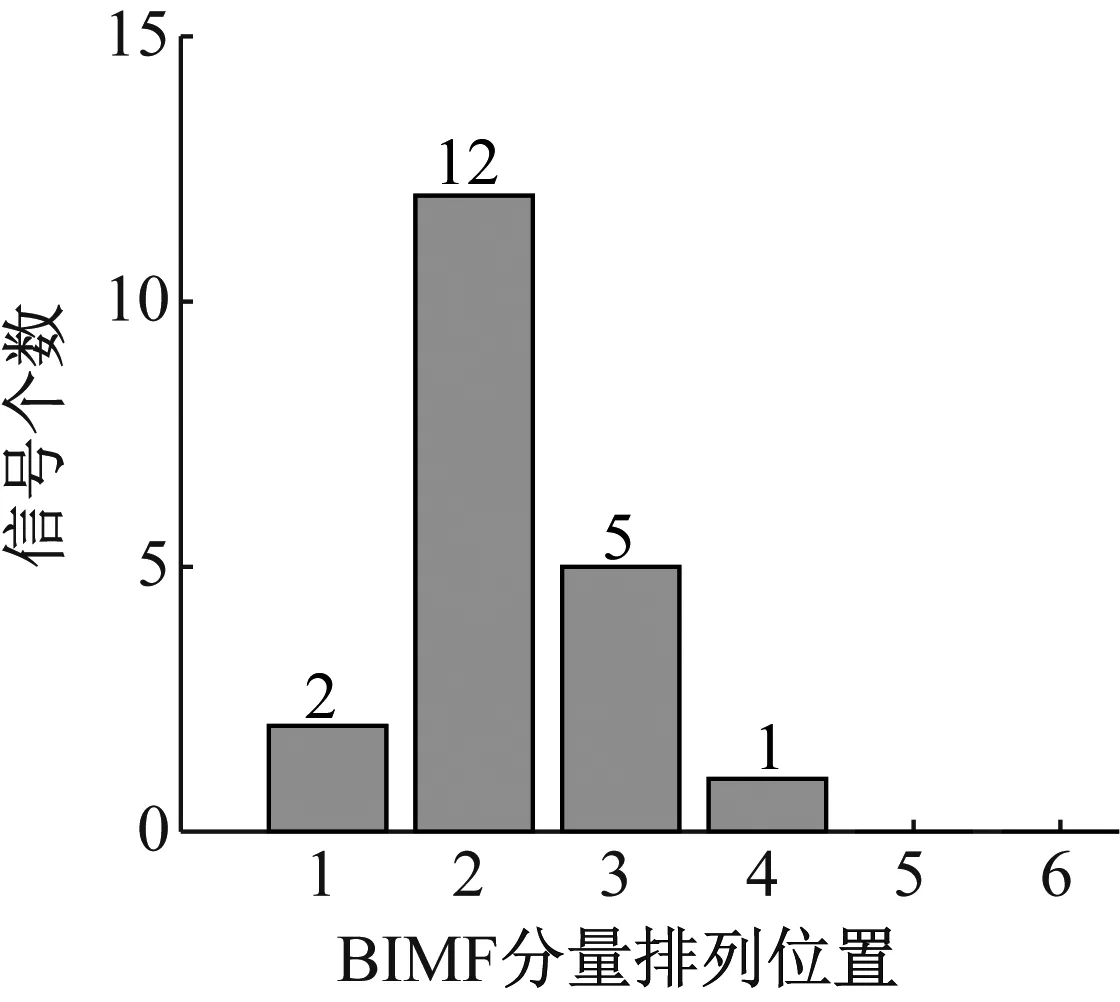
圖19 20組實驗信號中故障信息所在的BIMF分量及其個數

Fig.19 The BIMF components and the numbers of the fault information in the 20 experimental signals

為了進一步驗證FA-PMA-VMD方法可以將含豐富故障信息的BIMF分量靠前排列，選取與實驗信號同一測點但不同時間段獲取的20組信號。用FA-PMA-VMD方法對這些信號進行分解。然后以故障信息所在的分量的排列順序號為x軸，x對應的信號的個數(含有故障信息的同一順序號的BIMF分量個數)為y軸建立直方圖如圖19所示。可以觀察到這20組試驗信號經過FA-PMA-VMD方法分解后獲得的20組BIMF分量中，故障信息所在的分量主要集中在每組分量的前三項，表明FA-PMA-VMD方法可以將含豐富故障信息的BIMF分量靠前排列。

4 結 論

(1) 本文針對VMD方法分解所得BIMF分量排序不規律的問題，提出了PMA-VMD的方法，把主模態分析與VMD方法結合起來，根據故障特征來對BIMF分量進行排序，可將含豐富故障信息的BIMF分量靠前排列。對于大量BIMF分量組中含故障信息的BIMF分量的甄別具有指導意義。

(2) 針對PMA-VMD中[k,α]參數的選取對分解結果影響較大的問題，引入螢火蟲算法，提出FA-PMA-VMD方法對參數[k,α]進行組合優化。并在仿真信號中證明了此方法的可行性。

(3) 用FA-PMA-VMD方法對與帶齒根裂紋的齒輪振動實際信號進行分析，提取了有效的故障特征，得到了準確的診斷結果。具有一定的實用性。