鉛酸電池剩余放電時間預測的數學模型
宋劍萍
(西安職業技術學院基礎課部,陜西西安710077)
2016全國大學生數學建模競賽C題,電池剩余放電時間預測。本文根據題目中所給定的電池放電采樣數據,研究鉛酸電池放電數學模型的建立和剩余放電時間的預測。
1 問題重述
鉛酸電池作為電源,被廣泛用于日常生活、工業、軍事中。鉛酸電池在恒定電流強度荷載的放電過程中,電壓隨著放電時間單調下降,直到最低保護的額定電壓(Um=9 V)。從充滿電后開始放電,電壓隨時間變化的關系稱為放電曲線[1]。
問題一根據同一生產批次的電池,出廠時以不同電流強度荷載,放電測試記錄數據。用初等函數建立放電數學模型,并用模型的平均相對誤差MRE檢驗其精度。根據建立的模型,預測新電池分別以30 A、40 A、50 A、60 A和70 A電流強度放電,從電壓為9.8 V降到9 V時的剩余放電時間。
問題二依據任一恒定電流強度荷載下電池放電的數學模型,繪出電流強度為55 A時的放電曲線圖,并寫出其數學表達式。
問題三根據不同的衰減狀態,以同一恒定電流強度荷載的同一電池,從充滿電后開始放電的采樣數據。預測電池在衰減狀態3的剩余放電時間。
2 數據分析
根據題目中給出的生產同一批次電池,出廠時以不同電流強度放電,經測試得到完整放電曲線的采樣數據。將其數據導入MATLAB軟件中,使用程序為:
x1=xlsread(′CUMCM2016-C-Appendix-Chinese.xlsx′,′,exc1′,′A7:A1885′);
可得電池在不同電流強度狀態下,放電時間與電壓關系的散點圖,如圖1所示[2]。
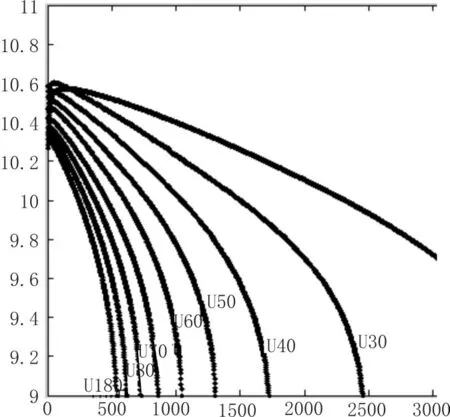
圖1 不同電流強度,時間與電壓的散點圖
因采樣數據點較多,數軸上的長度單位較小,所以圖1的散點圖給人以曲線圖的感覺。圖1得出,電流強度越大,電壓隨時間下降的越快。即電池以不同的恒定電流強度放電時,電流強度越大,其放電時間越短。電流強度越小,其放電時間越長。
3 恒定電流下,模型建立與求解
根據圖1不同的恒定電流下,電池的放電散點圖和題目要求用初等函數表示放電曲線,所以放電模型一為:

3.1 恒定電流下,放電模型建立
平均相對誤差MRE的計算公式為:
MRE=,其中Z為實際剩余放電時間,Z′為理論剩余放電時間,n為樣本點的數量。
題目要求用基本初等函數建立數學模型,基本初等函數有三角函數,對數函數,指數函數,冪函數以及它們的四則運算,根據圖1猜測,電池的放電曲線是多項式函數。
采用MATLAB軟件工具箱中的多形式擬合命令,擬合出放電曲線的多項式函數。
因100 A電流強度放電時的時間和電壓數據比較少,所以對它分別采用了二次曲線和三次曲線擬合,二者的擬合系數都在99以上。但是,用MATLAB程序計算這兩條曲線的平均相對誤差MRE分別為10.986 7和0.046 3。這兩個數據說明,采用二次曲線擬合時,實際放電時間與理論放電時間差別較大,超過了百分之百的誤差,而三次曲線擬合的MRE誤差在5%以下,說明三次曲線擬合得到的理論放電時間更接近于實際值。因此選用三次曲線擬合最佳[3-4]。
效仿100A電流強度下,電池放電曲線的三次多項式擬合方法,得到不同恒定電流下,電池的放電模型均采用三次多項式擬合。得到20 A,30 A,40 A,50 A,60 A,70 A,80 A,90 A,100 A 9種電流下的放電模型二為:

(其中u為電壓,t為放電時間,α,β,γ,λ分別是多項式的系數,n取1到9之間的整數)
3.2 恒定電流下,放電模型求解
圖1直觀顯示,時間與電壓的關系可分為3個階段:電壓隨放電時間急速下降階段,電壓隨放電時間單調上升階段,這是由于剛開始使用電池時,電池內物質的化學反應還沒達到穩定狀態所造成的。當電池放點持續一小段時間后,電壓隨放電時間進入單調下降階段。電池在放電初期,電壓隨放電時間急速下降和單調上升階段,這與題目中的要求“在鉛酸電池以恒定電流強度放電過程中,電壓隨放電時間單調下降”矛盾。電壓隨放電時間急速下降和單調上升階段不考慮,刪除不考慮階段的數據。將下降階段的整理后導入MATLAB軟件,建立初等函數數學模型,擬合放電曲線如圖2所示。本文僅僅從電壓隨放電時間下降階段開始研究[5]。

圖2 不同電流強度的放電曲線
運用MATLAB軟件工具箱中的擬合編程,分別得到20 A,30 A,40 A,50 A,60 A,70 A,80 A,90 A,100 A的放電曲線數學模型三如下:

根據平均相對誤差MRE的定義編程,得到上述各模型的放電曲線的平均相對誤差NRE值,如表1[6-7]。

表1 不同恒定電流下放電時間模型的MRE值表
上表中的數據說明,擬合得到的理論放電曲線與實際放電的記錄數據誤差在5%以下,放電曲線模型可以作為實際放電時間預測的理論根據。
根據上面的放電曲線模型三,將電壓分別是9.8 V和9 V帶入等式左邊,得到關于未知數為t的方程。用MATLAB軟件解方程得到對應的放電時間,如表1[8]。
電池的剩余放電時間=9 V所用放電時間—9.8 V所用放電時間。
在新電池使用中,分別以30 A、40 A、50 A、60 A和70 A電流強度放電,測得電壓都為9.8 V時,根據建立的數學模型,得到電池的剩余放電時間分別是:605 min,434 min,331 min,277 min,251 min。這與現實情況中,電流荷載越大,電池的使用時間越短是一致的。
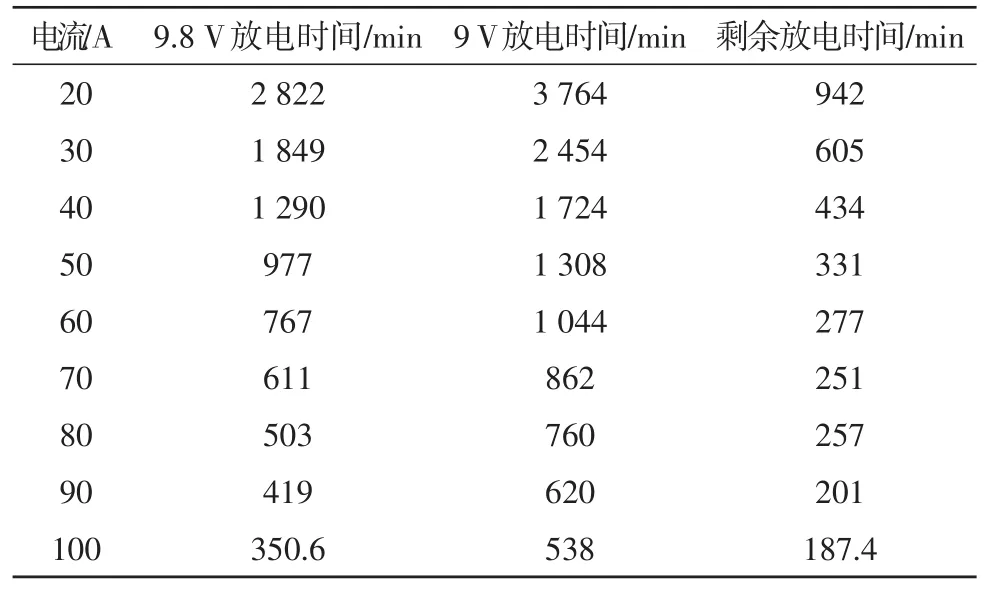
表2 電壓為9.8 V和9 V放電時間
4 任一恒定電流下,放電模型建立與求解
問題一是給定的恒定電流強度下放電曲線數學模型,建立的數學模型中有兩個變量,即電壓u和放電時間t。而問題二要求的是任一恒定電流強度下放電曲線數學模型,有3個變量,即電壓u,放電時間t和電流i[9]。建立如下模型四:

4.1 任一恒定電流下,放電模型建立
u=?(i,t)是二元非線性擬合,如果整體去擬合,難度大,并且積累起來的誤差比較大,所以采用逐步擬合的方法[10-11]。
利用(2)中各項系數α,β,γ,λ與電流i的之間的數據,即 (αn,in),(βn,in),(γn,in),(λn,in).用 MATLAB軟件工具箱中的擬合命令,建立各項系數α,β,γ,λ與電流i的函數關系[12]。即

得到任一恒定電流強度下放電曲線模型五為:
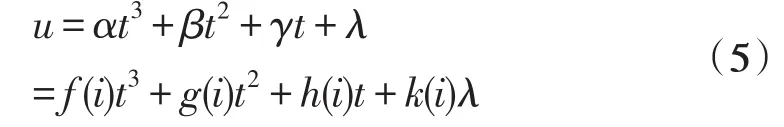
(其中u為電壓,t為放電時間,i為電流強度)
4.2 任一恒定電流下,放電模型求解
把i=50帶入式(4)中,得到平均相對誤差MRE為0.0097。說明模型五的建立是比較合理的[13]。
把i=55帶入式(4)中,得到電流為55A時的放電曲線函數表達式(6)和圖3:
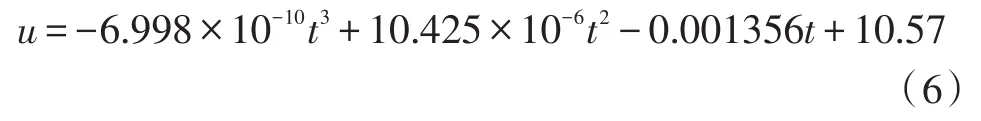

圖3 電流為55 A時的放電曲線
5 同一電流強度不同衰減狀態,放電模型建立與求解
由同一電池以同一電流強度的荷載,在不同衰減狀態下的,從充滿電后開始放電。根據電池放電時間與電壓的數據,建立新電池狀態、衰減狀態1、衰減狀態2 3種狀態的放電曲線,找出它們的放電曲線規律,預測衰減狀態3的放電曲線規律,從而得到衰減狀態3的未知放電時間。
5.1 同一電流強度不同衰減狀態的模型建立
根據放電電壓與時間的數據,使用MATLAB軟件,分別做出3種狀態的放電時間隨電壓變化的散點圖,如圖4所示[14]。

圖4 不同狀態,同一電流強度時間與電壓的散點圖
對圖4進行跟蹤定點,得出驟變節點坐標在10.4 V處。由驟變節點可以將圖像分為兩部分,電壓在10.4 V到10.5 V之間內,放電時間降低緩慢,3條曲線幾乎重合,可推出,在同一電流強度放電的情況下,電池的放電曲線差別甚微。當電壓u<10.4 V時,新電池狀態、衰減狀態1、衰減狀態2的放電曲線的趨勢大致相同,3種狀態放電曲線的趨勢大致相同,推測衰減狀態3的放電曲線與他們有相同的走勢。利用衰減狀態3的中已知放電時間與電壓的數據,擬合出的狀態3的放電曲線[15]。建立如下模型六

5.2 同一電流強度不同狀態的模型求解
根據圖4和建立模型六的過程分析,將衰減狀態3中的已知數值,帶入模型五中,通過曲線擬合得到衰減狀態3的放電曲線的函數表達式(8)如下:

其中,α=-156.9(-200.9,-112.8),β=4181(2848,5514),γ=-3.734×104(-5.078×104,-2.39×104),λ=1.126×105(6.738×104,1.577×105)。
在衰減狀態3下,電池的剩余放電時間t=tu=9-tu=9.765.所以,電池在衰減狀態3下的剩余放電時間為t=264.7min[16]。
6 結束語
本文依據采樣數據,運用MATLAB軟件,采用3次多項式擬合,建立了鉛酸電池在多種狀態下的放電曲線模型,對所建立的模型進行求解,用平均相對誤差MRE指標進行檢驗。該模型的建立,方法簡單易于操作,對電池放電時間的研究有一定的幫助和借鑒意義。

