大跨斜拉橋縱向地震碰撞響應參數(shù)分析

劉秀珍

（山西省交通科學研究院，山西 太原 030006）

橋梁結構的碰撞問題是橋墩及基礎平面撓曲振動在墩頂?shù)奈灰瞥^梁間伸縮縫寬度造成[1-2]。地震波激勵在傳播方向上經歷地質和路徑的不同，勢必會造成橋梁地震響應特征值的不同。由此造成梁體碰撞的主動碰撞體有所差異。在此基礎上，相鄰聯(lián)梁段自身周期大小和周期比被認為是影響碰撞效應的重要參數(shù)。周光偉等[3]對行波輸入下連續(xù)梁橋不同周期的墩梁相對位移碰撞效應進行了分析，指出當周期比較小(T1/T2＜0.5)時，碰撞效應最大，當周期比較大(T1/T2＞0.7)時，碰撞效應較大，而介乎中間的周期比的碰撞效應則較小。王軍文等[4]對相鄰梁體的周期比、基本周期大小、相鄰聯(lián)的質量比、伸縮縫間隙大小以及墩柱的彈塑性等因素進行了分析，但僅針對結構形式較簡單的梁橋分析，沒有考慮大跨徑斜拉橋結構特點對碰撞響應的影響。李建中等[5]也對橋梁碰撞方面進行了深入的研究，取得了一定的研究成果。鄧玉林等[6]提出主引橋極易發(fā)生碰撞，碰撞不僅會產生很大的撞擊，而且使引橋地震力需求、引橋梁端位移以及引橋梁體搭接長度需求有較大增長，但沒有考慮主引橋周期比這一影響地震碰撞反應的主要因素。

針對上述情況，本文考慮地震波傳播的方向性，基于主引橋周期不一致而表現(xiàn)出的動力特性差異，建立主引橋伸縮縫處碰撞效應非線性計算模型。以一座大跨斜拉橋與左右引橋地震碰撞響應為例，研究了縱向地震作用下主引橋碰撞效應影響規(guī)律，為橋梁的抗震安全性評估和抗震設計提供一定的參考。

1 計算模型

本文選取一座雙塔面漂浮體系斜拉橋為代表進行相關研究。該橋橋跨布置如圖1所示，跨徑組合為左右對稱形式，具體為45+67+416+67+45=640 m，左右引橋均為4×40 m等截面預應力混凝土箱梁結構。

圖1 橋梁總體布置圖

為便于分析周期比對主引橋碰撞響應規(guī)律的影響，主引橋的碰撞問題簡化為主動碰撞桿件一端正面垂直撞擊平整剛性桿件（靶體）問題。其中，將左引橋、主橋和右引橋分別擬化為彈性桿件1、彈性桿件2和彈性桿件3，引入等效彈簧剛度的概念，橋墩對主梁的抗推剛度等效為一定剛度的彈簧。

為方便推導，對下列符號作如下說明：kc1為左引橋等效彈簧剛度；kc2為主橋等效彈簧的剛度；kc3為右橋等效彈簧的剛度；kt為伸縮縫碰撞彈簧的剛度；l1為左引橋等效桿件長度；l2為主橋等效桿件長度；l3為右引橋等效桿件長度[7-8]。假設主引橋具有相同的截面形式A、質量密度ρ和楊氏模量E；主動碰撞桿件的彈性波速和被動碰撞桿件中壓縮彈性波的傳播速度均取

設定碰撞彈簧剛度遠大于引橋等效彈簧剛度，由系統(tǒng)運動微分方程組

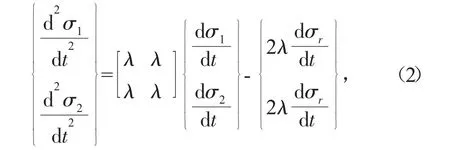
根據(jù)波陣面的動量守恒條件，主動碰撞體碰撞前為向靶體運動V0，即右行波。而碰撞瞬間，碰撞體的運動速度由兩部分組成：a）碰撞端部由于接觸應力的作用而引起的向左方后退速度為c,即左行波。b）左行波波面的前方是無應力區(qū)，在接這個區(qū)域的材料仍以原速度v0向靶體運動。靶體由接觸應力的作用而引起的向右方后退速度為v1，則：

左右兩側同時乘以ρc，根據(jù)波動面的動量守恒條件

式中：σ1=ρcv為彈簧固有頻率平方1，為彈性撞擊后，碰撞體和靶體之間的接觸應力；

σ0=ρcv0，為碰撞體仍以原速度v0運動部分產生的應力；

σl=ρcc，為以聲速c由碰撞接觸端沿左方向傳播產生的應力。

由于本文僅考慮主引橋周期比對橋梁碰撞力峰值和位移峰值的影響，忽略彈塑性交界面對梁體影響，碰撞后主碰撞體以左行波速度移動，式（4）簡化為：

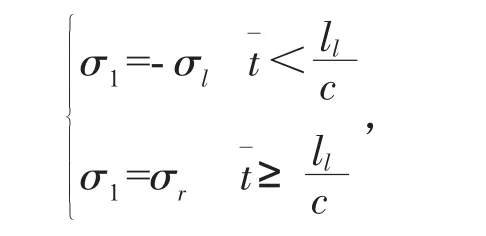
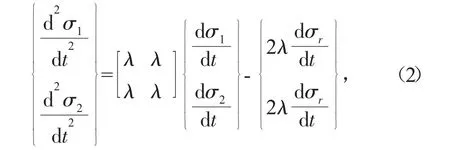
由桿件的基本周期T=2l/c，周期比可等效為：

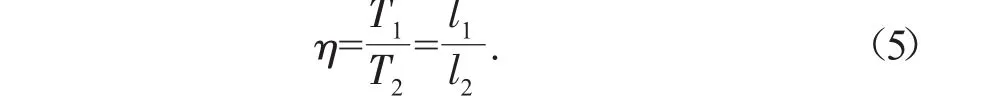
1.1 左引橋為主動碰撞體，主橋為靶體

a）η≤0.5 時（即 l2＞2l1），σ2被認為始終是右行波，

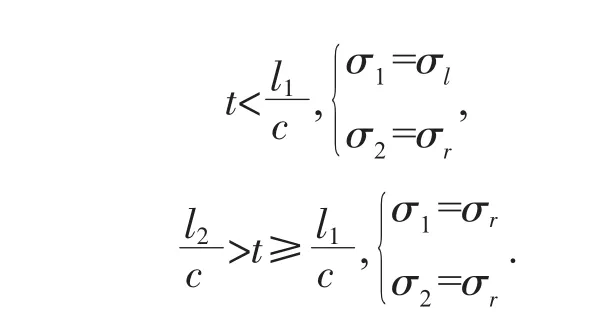
b）1≥η＞0.5 時（即 2l1≥l2＞l1），

1.2 主橋為主動碰撞體，右引橋為靶體時，周期比η′=T2/T3

a）η′≤0.5 時（即 l2＞2l3），

b）1≥η′＞0.5 時（即 2l3≥l2＞l3），

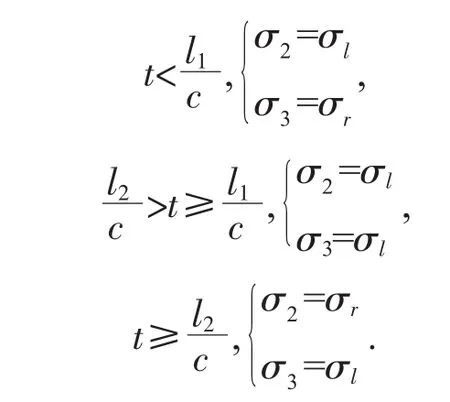
主引橋間碰撞彈簧采用接觸單元模擬。碰撞剛度取較短主梁縱向剛度[6]，恢復系數(shù)e取為1.0，即不考慮碰撞過程中的能量耗散。左引橋、主橋和右引橋的質量分別記為m1、m2和m3，基本周期記為T1、T2和T3，伸縮縫阻尼分別記為c1和c2，阻尼系統(tǒng)采用Rayleigh阻尼進行線性和非線性時程分析，伸縮縫間隙均為gp。具體如圖2所示。

圖2 簡化碰撞模型

1.3 主引橋碰撞過程存在的模式

考慮地震波的行波效應，行波速度方向的差異會導致主引橋的碰撞過程存在不同的模式，具體可分為：

a）工況1 以圖2a所示的動力計算模型考慮左引橋為主動碰撞體，該模型忽略右引橋的影響，只考慮左引橋與主橋之間的碰撞作用。

b）工況2 不考慮主橋與左引橋伸縮縫處的碰撞效應，簡稱左引橋無碰撞。

c）工況3 以圖2b所示的動力計算模型考慮主橋為主動碰撞體，該模型忽略左引橋的影響，只考慮右引橋與主橋之間的碰撞作用。

d）工況4 不考慮主橋與右引橋伸縮縫處的碰撞效應，簡稱右引橋無碰撞。

2 地震波輸入

為分析地震作用下的橋梁響應規(guī)律，選取了4條不同加速度時程從而分析碰撞效應對橋梁抗震性能的影響。

表1 選取的地震波

3 碰撞效應對橋梁抗震性能的影響

3.1 考慮碰撞效應對主橋的影響

圖3、圖4給出了工況1作用下考慮碰撞效應時主橋索塔塔頂位移比、索塔根部彎矩比隨周期比變化曲線。

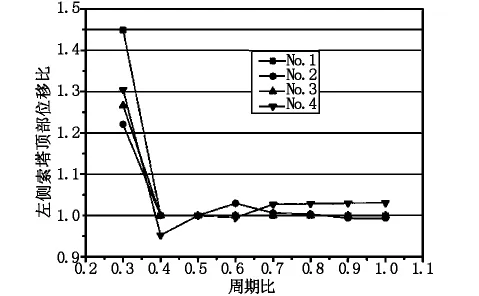
圖3 左側索塔塔頂相對位移比

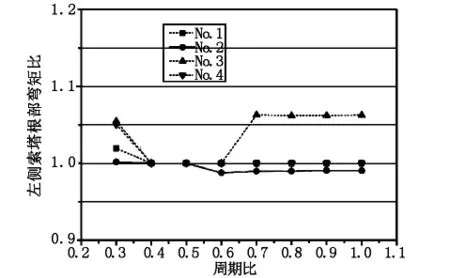
圖4 左側索塔根部彎矩比

由圖3可知，引橋對主橋的單邊碰撞效應導致索塔塔頂產生位移，左引橋基本周期T1越低，碰撞效應對索塔塔頂位移影響越大，但隨著周期比T1/T2的增加，碰撞效應的影響整體趨于減小，這也驗證了周期比是影響長周期橋梁地震碰撞效應的主要因素。由圖4可知，左引橋基本周期T1越低，碰撞效應對索塔根部彎矩的影響越大，這與索塔頂部位移趨勢保持一致。但隨著周期比T1/T2的增大，碰撞效應影響趨于復雜，索塔根部彎矩比有可能增大（如地震波No.3的影響曲線），也有可能減少，但增幅不大，整體上保持碰撞效應不斷減小的趨勢。因此，地震作用下的碰撞效應對大跨徑斜拉橋的影響較小，不會造成主橋結構地震需求的明顯增大。

圖5 右側索塔塔頂相對位移比

圖6 右側索塔根部彎矩比

圖5、圖6則給出了工況3作用下考慮碰撞效應時主橋索塔塔頂位移比、索塔根部彎矩比隨周期比變化曲線。對比圖3、圖4的變化曲線，工況3作用下主橋的碰撞效應影響較工況1時偏小，索塔塔頂位移比和根部彎矩比影響雖然也有所增大，但增大幅度小于工況1。特別是當周期比T1/T2＜0.5時，索塔塔頂相對位移比和根部彎矩比均小于1，此時碰撞效應反而減小地震導致的塔頂位移和索塔根部彎矩。因此，工況1和工況3兩種不同碰撞模式對主橋抗震效應會產生不同的影響，工況1影響效果大于工況3。

3.2 考慮碰撞對引橋的影響

圖7給出了工況1和工況3作用下伸縮縫處碰撞力峰值的比較圖。圖7表明，即使相同地震波作用下，不同主動碰撞體發(fā)生的單邊碰撞，產生的碰撞力峰值也會存在差異。工況3作用下碰撞過程更易激起較大的碰撞力，從而引起結構的震害也更為嚴重。這種差異表現(xiàn)將隨著地震波有效加速度峰值和持續(xù)時間的增大而增大。由于大跨徑斜拉橋的主梁質量大于引橋梁體，則在慣性作用下的碰撞強度加大，產生的碰撞力峰值也較大。

圖7 伸縮縫處碰撞力峰值曲線

圖8、圖9給出了工況1作用下，考慮碰撞效應時左引橋梁端相對主橋位移比和梁端位移比的變化曲線。

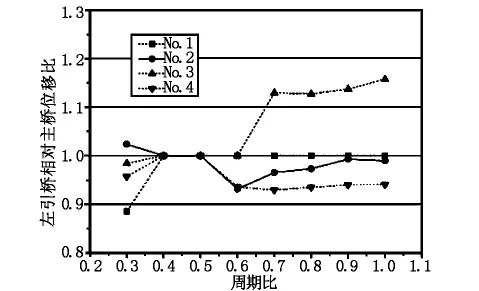
圖8 左引橋相對主橋位移比曲線

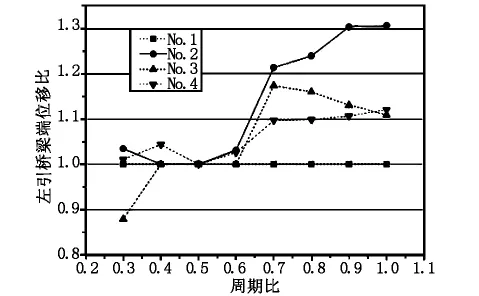
圖9 左引橋梁端位移比曲線

由圖8可以看出，在地震作用下，考慮引橋與主橋的周期比差異，不同縱向地震波引起伸縮縫處的非同向振動，形成引橋與斜拉橋主橋梁體相對位移的變化。單邊碰撞有時增大引橋梁端相對主橋位移，有時減小引橋梁端相對主橋位移，但總體影響不大。圖9則表明單邊碰撞作用下，左引橋梁端-過渡墩間的距離整體上隨著周期比的增加而增加。具體來說，當周期比T1/T2＜0.5時，碰撞效應影響不大，但當T1/T2＞0.5，碰撞效應則會使得左引橋梁端位移明顯增大，且碰撞效應對梁端位移影響隨周期比的增大而增大。

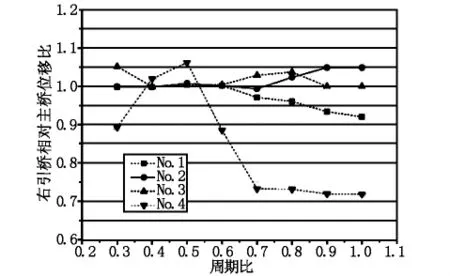
圖10 右引橋相對主橋位移比曲線

圖10、圖11分別給出了工況3作用下右引橋梁端相對主橋位移比和梁端位移比的變化曲線。由圖12和圖13可以看出，當T3/T1＜0.5時，碰撞效應對引橋梁端相對主橋位移比和梁端位移比影響不大。當T3/T1＞0.5時，總體上梁體碰撞效應隨主引橋周期比的增加而減小，但幅度變化不大。對比工況1和工況3對應的梁端相對主橋位移比和梁端位移比曲線可以發(fā)現(xiàn)，引橋單邊碰撞與主橋單邊碰撞呈現(xiàn)完全相反的結果，引橋單邊碰撞效應明顯大于主橋單邊碰撞效應，這也說明碰撞效應的不同源于地震波的縱向傳播方向的不同。

圖12 左引橋墩底彎矩比曲線

圖13 右引橋墩底彎矩比曲線

由圖12和圖13可以看出，考慮單邊碰撞作用，總體上將使引橋墩底地震響應增大，但增加幅度較小，相比較而言，工況1作用下墩底響應整體上隨周期比的增大而增大，而工況3作用下的引橋影響規(guī)律較為復雜，隨周期比的增加，碰撞效應的比值可能增加，也可能減小，這與地震波有效加速度峰值和持續(xù)時間有關。

4 結論

a）引橋基本周期T1越低，碰撞效應對索塔影響越大，但隨著周期比T1/T2的增加，碰撞效應的影響整體趨于減小。

b）主橋為主動碰撞體的碰撞效應會對增加主橋抗震位移和彎矩參數(shù)需求，但增大幅度小于引橋為主動碰撞體的碰撞效應，即后者的影響效果大于前者。

c）即使相同地震波作用下，不同主動碰撞體發(fā)生的單邊碰撞，產生的碰撞力峰值也會存在差異。主橋為主動碰撞體的碰撞過程更易激起較大的碰撞力，從而引起結構的震害也更為嚴重。這種差異表現(xiàn)將隨著地震波有效加速度峰值和持續(xù)時間的增大而增大。

d）引橋單邊碰撞與主橋單邊碰撞在梁體位移影響上呈現(xiàn)完全相反的結果，引橋單邊碰撞效應明顯大于主橋單邊碰撞效應，這也說明碰撞效應的不同源于地震波的縱向傳播方向的不同。