變換參考系巧解一道物理競賽題

李常明

(鳳凰縣高級中學(xué),湖南 鳳凰 416200)

拋體運動是全國中學(xué)生物理競賽常考題型之一.經(jīng)典的解題方法是將拋體運動分解為兩個直線運動求解．這類題型若能充分利用中學(xué)物理所學(xué)方法,大部分情況能化繁為簡達(dá)到快速求解的目的．筆者在給學(xué)生競賽輔導(dǎo)中發(fā)現(xiàn)第32屆拋體類競賽試題有更基礎(chǔ)、簡單、易懂的解法,現(xiàn)簡要分析如下．

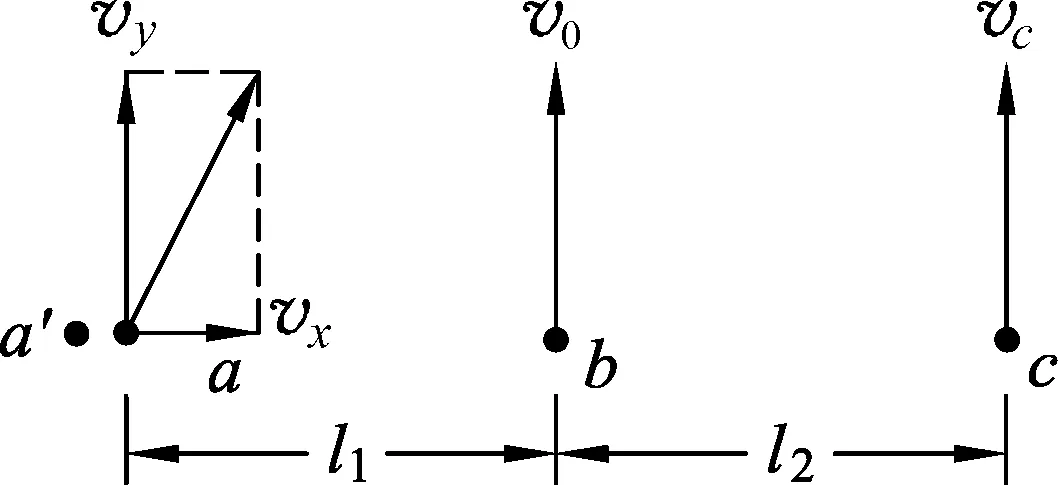
圖1

原題.從左至右在同一水平地面上依次有3個質(zhì)點a、b、c,且3者共線,a與b相距l(xiāng)1,b與c相距l(xiāng)2．現(xiàn)同時將它們從其初始位置拋出．已知質(zhì)點b以初速度v0豎直上拋,質(zhì)點c以某一初速度豎直上拋．設(shè)在這3個質(zhì)點的運動過程中,a能碰到質(zhì)點b和c;并假設(shè)質(zhì)點a的質(zhì)量遠(yuǎn)大于質(zhì)點b的質(zhì)量,且a與b碰撞時間極短．求質(zhì)點c的初速度vc和質(zhì)點a的初速度所滿足的條件．所求的結(jié)果均用題中的已知量表示出來．

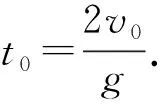
由以上解法可知適當(dāng)變換參考系,在動力學(xué)中選非慣性參考要引入慣性力解題不一定方便,但是在運動學(xué)中引入非慣性參考,增加了思維含量,運算與書寫過程則變得非常簡潔,其難度也由較難的競賽試題變得像一道簡易的直線運動基礎(chǔ)習(xí)題．