基于KFCM和AMDE-LSSVM的軟測量建模方法

，，，

(江蘇大學 電氣信息工程學院，江蘇 鎮江 212013)

0 引言

發酵過程涉及微生物生長繁殖，過程呈現高度非線性和不確定性；同時隨著發酵進行，發酵最適條件參數隨時間發生改變，使得傳統的傳感器方法難以實時在線檢測發酵過程關鍵參數，從而造成無法對發酵過程進行優化控制，自動化水平遠低于其他工業生產過程。因此“軟測量”建模被提出和廣泛應用在發酵工業中[1]。

最小二乘支持向量機(LS-SVM)建模方法采用結構風險最小化原則和核參數技術，同時建模速度較快，在解決小樣本的建模過程中有很好的表現[2-5]。實踐表明，LS-SVM模型過程中徑向基寬度和懲罰系數對建模性能影響很大。LU 等[6]采用量子粒子群算法來完成支持向量機參數選擇，并運用在發酵過程成中，取得很好測量效果；劉瑞蘭等[7]提出用遺傳算法對模型進行稀疏化以及參數尋優。這些算法不僅縮短了計算時間，而且降低了對初值選取的依賴度，但算法都比較復雜。差分進化(DE)算法利用隨機選擇的不同個體進行差分矢量運算對原始個體進行迭代優化，它是優化LS-SVM模型參數的一種合適的方法，它在收斂性和穩定性上都比其他算法有優勢。隨著差分進化算法迭代的進行，最優解容易陷入局部最優[8-10]。為了克服差分進化的缺陷，增加種群的規模是常用手段，該方法沒有從根本上解決早熟收斂的問題，增加種群規模同時增加算法了的運算時間。為了跳出局部收斂，改善DE算法的性能，本文針對差分進化中的局部最優解和交叉概率因子進行了優化。

在發酵過程中，隨著發酵過程的進行，發酵參數隨之改變，單一回歸模型不再適應新的工況，因此采用模糊C均值聚類(FCM)將數據劃分，再建立多個模型的多模型軟測量建模則顯得更加合理。梅從立等[11]將FCM與高斯過程回歸相結合，運用在紅霉素的生產發酵中，取得很好的效果。由于傳統FCM方法會導致某一聚類樣本過多，而另一類過少，從而分類的有效性下降。引入正定核函數，將輸入樣本數據映射到高維特征空間，得到基于核的模糊C均值聚類方法解決這一問題[12]。錢曉山等[13]將KFCM和LS-SVM相結合得出一種多模型軟測量建模方法，運用在蒸發過程的軟測量中，證明了KFCM對數據分類的有效性。陳貴華等[14]將多模型軟測量方法運用在乙烯裂解過程中，證明了多模型方法具有更好的精度和泛化能力。

本文將核模糊C均值聚類算法與AMDE-LSSVM相結合，提出的方法應用于秸稈發酵生產燃料乙醇過程中關鍵參量的測量，建立一種多模型(KFCM-AMDE-LSSVM)秸稈發酵過程軟測量模型，通過實際發酵工廠進行離線采集的數據，進行了軟測量仿真實驗。

1 算法描述

1.1 核模糊C均值聚類

假設存在樣本集：X={x1,x2,…,xn},創建聚類c，對于數據中與樣本集X相似的為一組；不相似的盡可能不在一組。通過求目標函數的最小值J來對數據進行分類[15-16]。

(1)

(2)

其中：c為聚類個數，vj為聚類中心，uij為數據xi對第j個聚類中心的隸屬度值，m為加權數。

引入非線性映射φ：x→φ(x)，特征空間的樣本距離定義為:

‖φ(xi)-φ(xj)‖2=K(xi,xj)+K(vj,vj)-2K(xi,vj)

(3)

其中：K為核函數。這里討論一種條件正定核：

K(x,y)=-(‖x-y‖2+b2)1/2，b∈R

(4)

令b=1,將正定核引入式(3)，可得目標函為：

(5)

構造拉格朗日函數，分別對v，u求偏導，得到的vj和U的更新公式如下：

(6)

1.2 基于AMDE-LSSVM的建模方法

1.2.1 最小二乘支持向量機

給定數據集{(xi,yi)|i=1，2，3....l}，xi∈Rn為n維樣本輸入，yi∈R為樣本輸出。通過對樣本數據逼近，函數擬合問題可以描述為最優化問題[17-18]:

(7)

式中，C為懲罰系數，e為允許誤差。引入拉格朗日算子對上式求解，得到

(8)

根據KKT條件，式(8)的一階導數為：

(9)

式(9)消去變量w、e，得線性方程組：

(10)

Q=[1,…,1]T,a=[a1,a2,…,al]T,y=[y1,y2,…,yl]T,

K為核函數矩陣。根據Mercer條件可以得核函數為：

K(xi,xj)=φ(xi)Tφ(xj)

(11)

綜上可以得到最終輸出為：

(12)

采用徑向基函數(RBF)：

(13)

其中：σ為徑向基寬度。

1.2.2 差分進化算法

差分進化算法是一種保留最優的貪婪算法，它由變異、交叉和選擇操作組成[19-20]。

(14)

其中：F為縮放因子。h1,h2,h3∈(1,2,…,NP)是互不相同且與i不同的隨機數。

(15)

其中：CR為范圍在[0,1]之間的交叉算子，rand(j)為[0,1]之間的隨機數。

3)在選擇操作中，按式(16)選擇新的種群個體。

(16)

其中：f(·)為目標函數。

1.2.3 自適應變異差分進化

本文選擇DE/best/2/bin策略。個體變異操作的方程為：

(17)

1.2.3.1 自適應二次變異思想

定義1 群體適應度方差為：

(18)

fi為第i個個體的適應度，favg顯示適應的程度，式中，f中是歸一化定標因子，其作用是限制群體適應度方差的大小，具體公式如下：

(19)

(20)

1.2.3.2 時變交叉概率因子CR。

由DE交叉操作可知，在搜索初期需要保持全局搜索能力，從而需要較小的CR，保持種群的多樣性；搜索的后期因已確定最優范圍，需要對局部進行精確搜索，從而需要較大的CR以保證搜索后期的搜索速度[9]。基于這種思想，在前期設定較小交叉概率因子CR，隨著搜索時間的增加而加大交叉概率因子CR。本文時變交叉概率因子CR由下式得到：

(21)

在算法設定初始交叉概率CRmin和最大交叉概率CRmax

1.2.4 基于AMDE-LSSVM建模

在LS-SVM中，懲罰系數C和徑向基寬度σ對模型的泛化能力有著很大的影響，因此尋求模型最佳懲罰系數與徑向基寬度是十分重要的。本文利用AMDE對LS-SVM建模中的參數進行選擇。

AMDE-LSSVM軟測量建模步驟如下：

2)初始化種群NP、變異算子F、最大迭代次數Gmax、初始交叉率CRmin、最大交叉概率CRmax、終止閾值、懲罰系數C和徑向基寬度σ的上、下值。令G=0，根據C和σ的上、下限產生一組隨機的[C1,σ1]。

5)G=G+1。

6)對[C,σ]進行變異、交叉、選擇操作。產生新的[C,σ]，返回步驟3)。

7)得到最優懲罰系數C和徑向基寬度σ作為建模參數，進行軟測量建模。

1.3 基于KFCM和AMDE-LSSVM軟測量建模

基于KFCM和AMDE-LSSVM軟測量建模思想在于：利用核模糊C均值聚類算法的有效分類，將采集的樣本數據集X分成{Xi|i=1,2,…,c}，c個聚類。對每一個Xi分別采用AMDE-LSSVM進行訓練，得到每一類的輸出為：

(22)

采用模糊隸屬度來綜合最后的結果：

(23)

式中uik為第k個樣本對應的第i類模糊隸屬度，fi(x)為第i個子模型。

秸稈發酵關鍵參量的多模型軟測量建模如圖1，步驟可如下描述：

步驟1：對采集數據進行預處理。

步驟2：將處理后的樣本用核模糊C均值聚類進行劃分為c個不同的子集。

步驟3：對每個聚類的樣本運用AMDE-LSSVM進行建模，得到c個秸稈發酵關鍵參量軟測量子模型。

步驟4：求得各個隸屬度，由式(19)得到最終的多模型軟測量輸出。

圖1 建模過程

2 實驗仿真

我國是世界上農作物秸稈類資源最多的國家，2015達到10.4億噸，其中20%為二次利用，而剩余大部分以堆積焚燒的方式處理。就地焚燒的處理方法，不僅給環境帶來極大污染，而且浪費了秸稈類資源的生物質能量。通過發酵的方式得到可保存的氣體或液體燃料，例如酒精、氫氣、柴油等，熱效率提升20%以上[22-23]。這樣不僅解決了污染問題，而且使農民得到了創收。近年來，秸稈發酵制取燃料乙醇規模化成為研究的熱點。乙醇濃度、總糖濃度、菌體濃度是觀察秸稈發酵過程的重要參數，但是無法通過物理傳感器檢測，制約了自動化水平的提升。因此將本文設計的多模型軟測量方法用于秸稈發酵的關鍵參量的測量中。

在建立秸稈發酵關鍵參量軟測量之前，必須對發酵機理進行分析，選取合適的輔助變量。秸稈發酵過程如圖2所示。根據課題組已有的成果選取：溶解氧、發酵液酸堿度、電機攪拌速度、空氣流量作為輔助變量。按照工藝要求，過程中罐溫控制在36 ℃±1 ℃，攪拌機轉速控制在120～180 r/min，通氣量為0.2 L/min，發酵罐壓控制在0.2 MPa±0.01 MPa。每隔1 h取樣并離線采集化驗乙醇濃度、總糖含量、菌體濃度。總共采集10批數據，其中前9批數據作為訓練數據，另外1批數據作為測試數據。軟測量模型建立完畢后,利用C語言編程實現，并嵌入到計算機中，當待預測罐批的輸入向量，經測量儀表讀入計算機后，利用軟測量程序計算得到關鍵狀態變量的預測值，并將預測結果經數據通道傳送到計算機上顯示，供操作人員進行觀察和控制發酵過程。

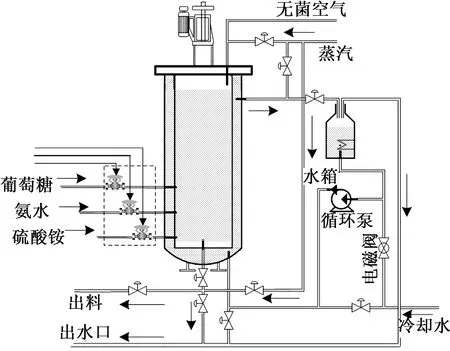
圖2 秸稈發酵過程

3 仿真結果與分析

設定分類個數c=3，加權數m=2，求出不同類相應的聚類中心v和隸屬度矩陣U。應用AMDE-LSSVM建立3個子模型。模型1的懲罰系數C=101.56，徑向基寬度σ=5.65；模型2的懲罰系數C=45.88，徑向基寬度σ=18.467；模型3的懲罰系數C=78.19，徑向基寬度σ=2.678。多模型輸出采用隸屬度加權策略。表1為幾種優化算法對比，表中的數據可見，AMDE算法在選擇LS-SVM的核參數優于交叉驗證和傳統DE算法，證明了AMDE算法的全局尋優能力。對比3種尋優方法的運行時間，AMDE和DE算法明顯要優于交叉驗證的方法。由于AMDE在結構上引入了時變的交叉概率因子，在算法搜索期間有不同的交叉概率因子，前期提高全局搜索能力后期提高局部搜索能力，從而加快了搜索時間。對于不同結果的標準差分析可以發現，AMDE的標準差最低，反映出設計的自適應二次變異思想有效地跳出傳統DE算法的早熟收斂。

基于KFCM和AMDE-LSSVM軟測量仿真結果如圖5所示，圖中顯示了離線化驗值、多模型軟測量預測值和DE-LSSVM軟測量預測值。從圖中可以明顯看出，DE-LSSVM軟測量方法預測值雖然在趨勢上接近離線化驗值，但是在發酵前期和后期有很大的誤差，這是因為在發酵秸稈發酵各個時期所表現的發酵最適條件不同，導致單一的模型失效。多模型軟測量方法預測值在發酵各個階段都表現出了良好的擬合精度，誤差更小，這是因為多模型方法是對秸稈發酵過程進行劃分得到多個模型，使得預測模型更加精確。發酵實際值與軟測量值的誤差如圖6所示，該圖進一步顯示了優化后的多模型軟測量方法在秸稈發酵關鍵參量的預測中表現更好。

表1 優化方法對比

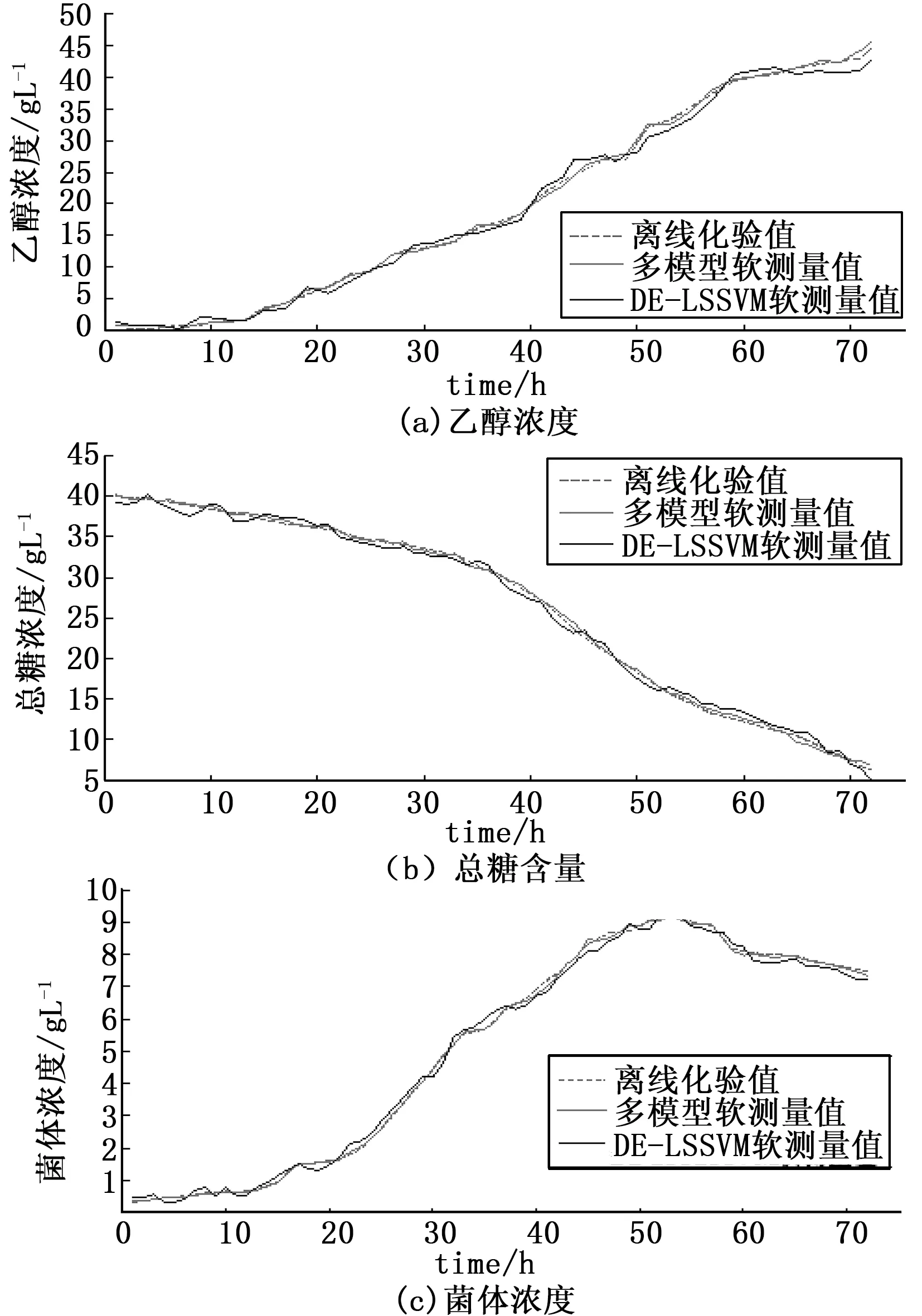
圖5 軟測量結果比較圖

圖6 相對誤差比較曲線

表2和表3是幾種不同算法下的性能比較。與BP、SVM、DE-LSSVM相比，改進后的多模型軟測量方法在乙醇濃度、總糖含量、菌體濃度的預測上標準誤差分別只有0.64%、1.85%、0.75%，與其他單一預測方法有了明顯的提高，并且訓練時間大幅度降低。詳細分析表2和表3中的DE-LSSVM建模和多模型建模，可以看出單一LS-SVM建模需要10.7 s，而本研究中建立3個子LS-SVM模型得到多模型雖然在時間上稍稍多于單個LS-SVM建模，但是在測量精度上要遠遠由于DE-LSSVM建模，可以滿足實際秸稈發酵過程關鍵參數測量的需要。

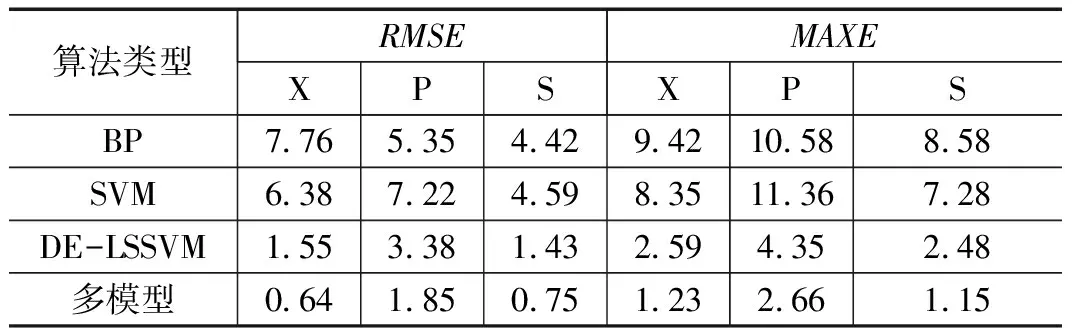
表2 不同算法的性能比較 %

表3 不同算法的訓練速度

4 結束語

針對發酵過程的復雜性、時變性，本文提出了發酵關鍵參量的多模型軟測量建模，運用KFCM將數據劃分為三類，分別建立LS-SVM模型，對于LS-SVM建立軟測量模型的不精確和常規交叉方法對選擇LS-SVM建模中懲罰系數C和徑向基寬度σ的盲目性和耗時性問題，本文引入DE算法對LS-SVM的參數進行尋優；同時針對DE算法存在易陷入局部最優和早熟收斂問題，提出一種自適應變異差分進化(AMDE)算法，該方法采用自適應變異操作和時變交叉概率因子對DE算法進行改進優化。通過仿真實驗顯示可以得到合適的懲罰系數C和徑向基寬度σ，并且提高了訓練的速度，最終得到的預測值的準確率有了明顯的提高。然而，本文算法的一個局限性就是使用的傳統KFCM算法對初始聚類中心初始值的設定的過分依賴性，通常的聚類算法往往對于不同的初始聚類中心會得到不同的聚類結果；二是需要預先設定聚類數目，這增加了算法的不確定性。因此下一步的研究方向可以針對這兩個問題進行開展。