一種高精度APNCKF算法在諧波檢測中的應用

，，，

(長沙理工大學 電氣與信息工程學院，長沙 410114 )

0 引言

諧波檢測是諧波問題中的一個重要分支，對諧波的分析和測量是電力系統分析和控制中的一項重要工作，也是治理諧波問題的出發點和主要依據[1]。準確而又快速地檢測出電力系統中的電力諧波,具有重要的工程實際意義[2]。

由于各種沖擊性負荷(高鐵等)、新能源(風電和光伏發電等)和電動汽車的接入，電網諧波實時精確檢測仍是電能質量測試技術的難點和熱點之一。常規的諧波檢測方法主要有：快速傅里葉變換及其改進算法、小波變換、HHT算法等[3-10]。DFT算法實用、穩定、有效，采用FFT可以提高算法的實時性[3]；但是頻率分辨率有限，對于臨近的頻率成分無法檢測[4]。改進算法中大多采用加窗譜線插值[5-6]，雖然加窗譜線插值FFT算法諧波參數的檢測精度較高，但是間諧波參數檢測卻相對較低，而且在低信噪比條件下，間諧波參數的檢測下降比較明顯[7]；譜估計算法對有限時寬的信號有無限的頻率分辨率，但需要進行大型矩陣運算，實時性不好，且需要對信號進行準確定階，對于電網寬帶多頻的信號無法直接檢測，穩定性不好；Prony 算法同樣受噪聲干擾的影響，諧波參數的檢測精度不高，在一定程度上限制了算法的實際應用[7-8]。小波變換和HHT可以實現非平穩的電力系統諧波分析；但是HHT 法在模態分解時存在模態混疊的現象，小波變換在用小波濾波器進行諧波分解時存在頻帶混疊現象，影響了算法的檢測精度[9-10]。IEC算法本質上是DFT的頻譜分組算法，精確計算的前提是盡可能實現同步采樣，實時性較好；但是僅僅針對諧波幅值的計算，沒有考慮諧波相位的計算。卡爾曼適用于平穩和非平穩過程，考慮到真實電網信號固有的隨機性和非平穩性[11]。卡爾曼已廣泛應用于頻率跟蹤、測量諧波分量、暫降等場合[12-13]。但是卡爾曼算法也存在一些難點，如噪聲統計特性的確定，特別是過程噪聲[14-15]。又如系統初始狀態和初始協方差的設置。通常情況下，過程噪聲統計特性(協方差)隨時間變化而變化，可能導致卡爾曼具有較大的估計誤差或甚至發散[16-17]。

為進一步提高含噪環境下諧波檢測的精確度，且不斷的在線辨識出過程噪聲協方差，提出了一種自適應過程噪聲協方差卡爾曼濾波算法(Adaptive Process Noise Covariance Kalman Filter ,APNCKF)。該算法利用序貫最大化可信度更新先驗信息，然后通過卡爾曼進行迭代運算，估計出相應的幅值和相位。通過在MATLAB環境下進行諧波仿真驗證，該算法在準穩態條件下較好地跟蹤電力系統諧波狀態，計算精度高。

1 APNCKF濾波的基本原理

卡爾曼濾波算法適用于線性系和部分非線性系統，被廣泛應用于諧波分量檢測、頻率跟蹤等場合。

1.1 APNCKF系統建模

電力系統中觀測信號包含基波、諧波和噪聲信號，可表述為:

(1)

式中，A1,k(r=2，…，M)、φr,k為r次諧波的幅值和相位，M為諧波的最高次數，ek為高斯噪聲信號。

若取如下狀態變量:

其中：

相應地，將觀測信號(1)可轉換成如下的狀態空間形式：

(2)

式中，ηk是均值為0方差為Qk的高斯白噪聲；vk是均值為0方差為Rk的高斯白噪聲。矩陣F，H，Qk，Rk分別定義為：

(3)

則各個頻率分量的幅值和相位可以由式(4)表示：

(4)

式中，x2r-1,k、x2r,k可以由模型(2)得到最優估計。

由卡爾曼濾波(Kalman Filter,KF)理論對諧波進行檢測的算法如下：

預測:

(5)

濾波:

(6)

1.2 APNCKF在線辨識過程噪聲

KF應用在諧波分量檢測時，過程噪聲統計特性(協方差)隨時間變化而變化，可能導致KF具有較大的估計誤差或甚至發散。針對噪聲統計特性的不確定性，本文采用序貫最大化可信度更新先驗信息的方法來在線辨識系統的過程噪聲，則使用模型(2)對xk進行最優估計時，KF具有較高的濾波精度。APNCKF方法認為噪聲均值為0，對噪聲二階中心矩(協方差)進行估計。

貝葉斯理論可知，可由下式估計噪聲Qk：

(7)

又因為Qk沒有先驗信息p(Qk|y1:k-1)，則可由最大化可信度密度函數p(yk|y1:k-1,Qk)來估計Qk，即為:

max{p(yk|y1:k-1,Qk)}

(8)

(9)

(10)

當qk=0時：

(11)

(12)

(13)

(14)

(15)

從而得到序列更新qk:

分析可知，只有15家高職高專院校圖書館對崗位職責給出了詳細描述，且集中在圖書流通和參考咨詢兩方面。同本科院校圖書館一樣，高職高專圖書館在其他需求上較為注重館員的工作經歷，不同的是，其對英語、計算機等相關證書沒有做出要求。

(16)

此方法只通過一個時刻的預測誤差來對過程噪聲協方差Qk進行修正，因此可信度不高。若利用多個時刻預測誤差的均值進行修正，則此方法更有效，更準確。設有N個時刻，則預測誤差均值為：

(17)

將式(18)代入式(17)可得:

(18)

其中：

(19)

因此，進行最優估計時，參數qk(或過程噪聲協方差Qk)的變化就能體現出信號的動態變化，從而實現諧波的跟蹤和檢測。且可由式(4)中狀態變量的幅值、相位曲線圖獲得基波和各次諧波的信息，對這些信息進行綜合判斷，統計分析，可以提高抗噪能力，增強魯棒性，提高對擾動時刻的準確性。

2 算例分析

本文通過常規卡爾曼、小波變換、KF-ML以及APNCKF進行仿真實驗，驗證APNCKF算法的在諧波檢測中的有效性，且該自適應算法的收斂速度、濾波精度及實時性顯著提升。

通過Matlab構造信號yt來模擬含有諧波的電壓信號，其由基波、3次、5次諧波以及不同信噪比噪聲疊加獲得，采樣頻率10 kHz。信號如圖1所示。

yk=E1,kcos(2πfkTs+φ1,k)+E3,kcos(6πfkTs+φ3,k)+E5,kcos(10πfkTs+φ5,k)+vk

(20)

其中：vt表示信噪比(SNR)值為40 dB，30 dB和20 dB的高斯白噪聲，即高斯白噪聲標準差分別為0.01 p.u，0.0316 p.u和0.1 p.u。電壓幅值Ei,t(i=1,3,5)和相位φi,k(i=1,3,5)模擬如下：

(21)

且:

(22)

顯然，諧波擾動發生的時間為0.04～0.16 s，且電壓暫降的時間為0.08～0.12 s。

圖1 諧波干擾的電壓信號(yt,y1,t,y2,t,y3,t分別為純凈，SNR為40 dB，30 dB和20 dB的電壓信號)

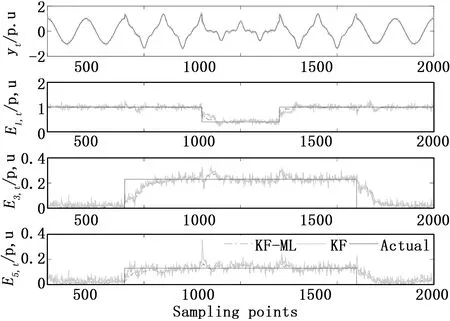
圖2 20 dB下KF-ML估計出的電壓信號(E1,t，E3,t，E5,t分別為基波，3次和5次諧波的幅值)

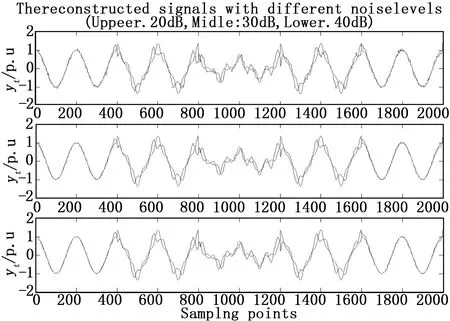
圖3 小波重構信號

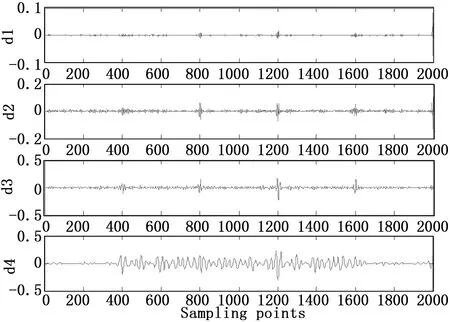
圖4 SNR=20 dB的四層小波分解

圖2給出了SNR=20 dB下KF-ML與常規KF對諧波的最優估計。圖3給出了實際信號與重構后的WT信號比較；圖4給出了SNR為20 dB時小波分解的結果。

從圖2可以看出常規KF在低信噪比時幅值曲線圖波動較大，對奇異值不能很好的跟蹤和檢測，精確度低。且常規KF的濾波性能依賴于系統噪聲的先驗統計信息，不準確的系統噪聲統計會導致KF濾波精度降低甚至發散。KF-ML算法則利用最大似然做為準則自適應地優化系統噪聲，從而提高其性能。從表1中可以看到KF-ML算法的RMSE值均小于KF和WT，這也驗證了KF-ML具有比KF更好的估計性能。但從圖2可知，KF-ML算法在基頻的幅值估計非常接近實際幅度，對電壓幅值響應也非常快速和準確；而在對諧波進行檢測時，相對于基頻的下降沿則表現出一些時延。其雖能比較準確地估計出諧波的幅值，但精度仍較差。

表1 不同算法的均方根誤差對比結果

圖3所示，由于諧波干擾，WT的重構信號明顯偏離實際信號。在圖4中，即SNR=20 dB時，小波系數d2，d3恰好在電壓暫降和諧波干擾處達到峰值，d4出現明顯的振蕩，表明在SNR=20 dB情況下，電壓暫降起止時小波系數峰值不明顯，這表明db4小波函數檢測性能隨著信號噪聲比的降低而變差。而從表1中也可以看到WT的RMSE值均高于KF和KF-ML。則隨著信號被噪聲和諧波嚴重污染時，WT精確度低、響應速度慢。

圖5 20 dB時APNCKF估計出電壓信號的幅值和相位

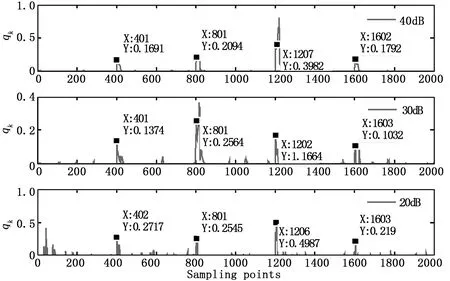
圖6 APNCPF中參數qk的變化過程

圖5為20 dB時APNCKF 估計出電壓信號的幅值和相位圖；圖6為APNCPF中參數qk的變化過程。由圖5可知，即使在高斯隨機噪聲比較強的情況下，APNCKF的估計信號與實際信號仍緊密匹配，進行很好地跟蹤與檢測。而KF估計的信號則具有一些不匹配的采樣點，例如在第400個采樣點與第500個采樣點之間、第800個采樣點與第900個采樣點之間、第1 200個采樣點與第1 300個采樣點之間以及在第1 600個采樣點與第1 700個采樣點之間，即發生諧波，電壓暫降和相位跳變的點與實際信號不匹配。因此，當跟蹤信號的突然變化時，KF的性能變差。對于幅值和相位的最優估計，即使這些干擾比較輕微，APNCKF對異常值(例如電壓暫降，相位跳躍或諧波干擾)的響應也快得多。這種精確地檢測為電力系統安全運行提供重要保證，這是因為APNCKF根據序貫最大化可信度更新先驗信息的方法來實時辨識系統的過程噪聲，對異常值(如諧波干擾或相位跳變)敏感。如圖6所示，每個子圖中有三組采樣點，其中參數突變非常接近諧波起止時間、電壓暫降以及相位跳變。因此，參數的動態變化可用于檢測諧波、相位跳變和電壓暫降。從表2可以看出，APNCKF在不同信噪比的情況下MAE和RMSE值均低于KF-ML，遠低于KF。這表明APNCKF可以獲得比傳統的KF和KF-ML更好的估計性能。與自適應KF-ML相比，參數qk對異常值敏感，它更容易檢測到干擾。因此，APNCKF優于用于檢測干擾的自適應KF-ML。

表2 不同算法誤差對比結果

3 結論

在電力系統諧波檢測中，系統隨機噪聲信息不完全可知，這可能會導致濾波器的估計精度不高；針對這一問題，采用序貫最大化可信度更新先驗信息來實時辨識系統過程噪聲，提出了一種自適應過程噪聲協方差卡爾曼濾波實現檢測電能質量擾動的時域方法。通過仿真和分析得出以下結論：

1)卡爾曼濾波器在進行諧波檢測時，時變的過程噪聲可能引起濾波精度低、甚至發散等問題，基于序貫最大化可信度更新先驗信息的方法來辨識系統的過程噪聲，提高了系統的穩定性以及檢測精度。

2)該算法與小波變換、常規卡爾曼以及基于最大似然準則的卡爾曼相比，當信號被隨機噪聲和諧波嚴重污染時，小波變換精確度低且響應速度慢；基于最大似然準則的卡爾曼在信噪比較低時，波動十分明顯，精度較差；而APNCKF在不同信噪比下MAE和RMSE值均較低，表現出較好的性能。

3)APNCPF中參數qk對異常值十分敏感。出現諧波干擾時，表現出不同幅度的峰值，更好的進行跟蹤與檢測，實時性強。