應用缺口件進行曲軸疲勞分析的可行性研究*

李建鋒，鐘劍鋒，孫嵩松，劉震濤*

(1.濰柴動力股份有限公司 內燃機可靠性國家重點實驗室，山東 濰坊 261061；2.浙江大學 動力機械及車輛工程研究所，浙江 杭州 310027)

0 引 言

隨著發動機強化程度的不斷提高，曲軸所承受的載荷越來越大，對其要求也越來越高。由于曲軸結構的復雜性，其應力集中十分嚴重，特別是在曲柄銷圓角和主軸頸圓角部位，曲軸失效位置也往往發生在這些部位，準確獲取曲軸的疲勞極限對曲軸疲勞可靠性研究具有重要意義[1-2]。

目前，常用疲勞試驗方法得到疲勞極限，但疲勞試驗往往存在試驗周期長、試驗成本高的問題。為了解決這些不足，國內外研究者們提出了臨界理論方法[3-4]、應力應變場強法、隱式梯度法、裂紋模擬方法[5-6]、等效標準缺口件等方法[7-11]，目的是更準確更有效地預測曲軸疲勞極限。裂紋模擬方法和等效標準缺口件方法的技術思路基本一致，都是將實際曲軸等效為某一標準體，但進一步的研究表明，等效標準缺口件方法比裂紋模擬方法精度更高，等效效果更好。等效標準缺口件的優勢在于可以將經過特殊工藝處理的實際構件等效為相同材料、相同工藝處理的標準缺口件，從而消除材料分散性和制造加工工藝等因素對等效疲勞分析結果的影響。

目前對缺口件的疲勞極限預測已有了大量的研究[12-16]，也達到了較高的精度，若能將曲軸等效為標準缺口件，則能夠應用缺口件對曲軸進行疲勞分析。

本文將對曲軸等效為圓形和橢圓形的標準缺口件進行優選設計，并對其等效的可信度進行試驗驗證。

1 曲軸單拐受力狀態分析

1.1 曲軸的有限元分析

以某型號曲軸為研究對象，建立曲軸單拐模型，利用有限元法對其進行受力分析，其有限元模型如圖1所示。

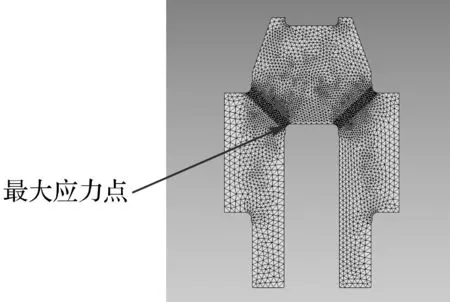
圖1 曲軸有限元模型

根據圣維南原理，曲軸的邊界條件可以等效為在曲軸的左主軸頸端面約束住所有的自由度，同時在對稱截面約束住平動自由度。曲軸的彎矩載荷施加在右截面，為試驗載荷的一半，曲軸圓角應力集中處在一個受力歷程內的應力計算結果如表1所示。

表1 曲軸圓角應力狀態的變化

表1中，拉伸和壓縮分別表示曲軸的曲柄圓角在受到對稱彎矩作用下，最大拉伸和壓縮應力；σm及Δσ分別表示曲軸圓角在一個受力歷程內的平均應力及應力幅值。

由表1可以看出：曲軸受到對稱循環載荷的作用。其載荷特征為：

(1)

式中：σmin—最小應力；σmax—最大應力。

1.2 曲軸的受力狀態分析

當材料所受應力狀態不同時，材料內部應力集中程度與塑性變形也將不同，因此，在曲軸疲勞分析中研究其內部的應力狀態，對研究曲軸的疲勞斷裂過程有著重要意義。

反映材料應力狀態的參數主要有應力三軸度η、應力Lode參數μ，以及應力狀態軟性系數α。其中，應力三軸度η是基于最小應變能密度因子理論而提出的，其物理含義在于材料的形變能密度最小處，其體變能最大，該處最容易發生疲勞斷裂，因此，選擇該參數作為應力狀態的表征量。

應力三軸度η的定義如下：

(2)

式中：σH—靜水壓力；σM—Von Mises應力。

本研究記錄從曲軸的最大應力點(如圖1連桿軸頸圓角所示)，深入到曲軸內部一段距離的應力值(沿黑線往最大應力點左上方)，共選取11個單元節點，標號為1，2…11，對其進行應力狀態分析，其曲軸應力梯度分布結果如圖2所示(后續分析圖表中橫坐標數字同樣表示相應的單元節點標號)。

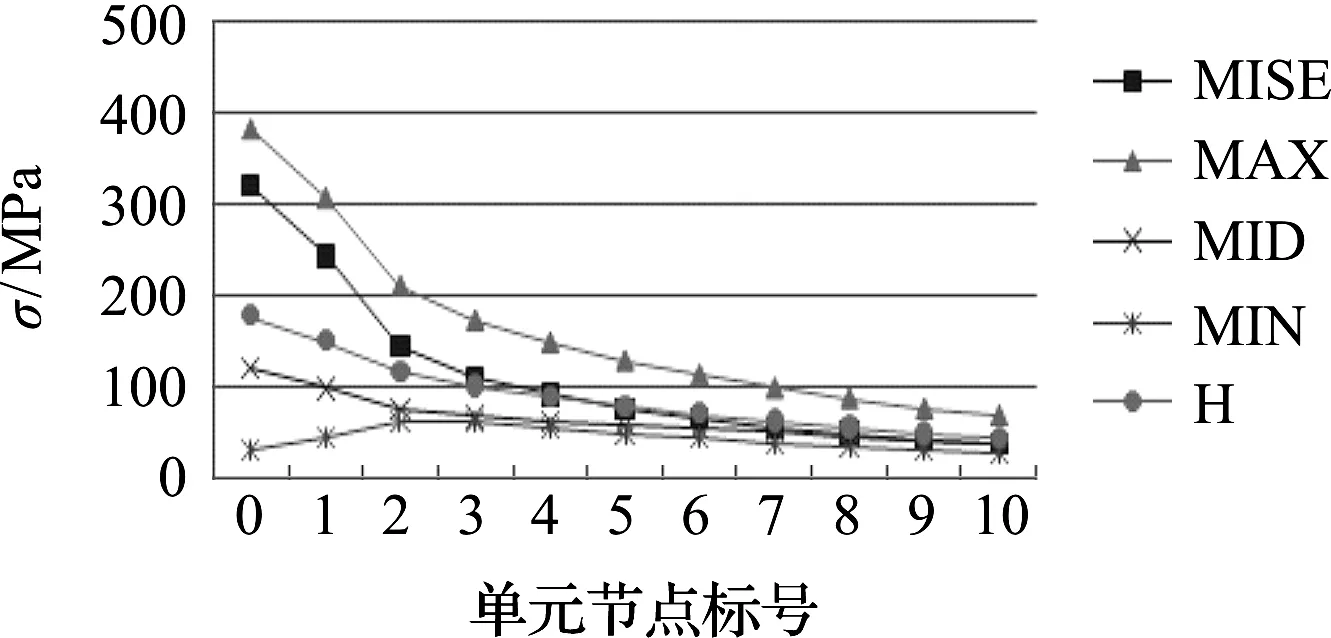
圖2 曲軸應力梯度分布

曲軸應力狀態分布如圖3所示。

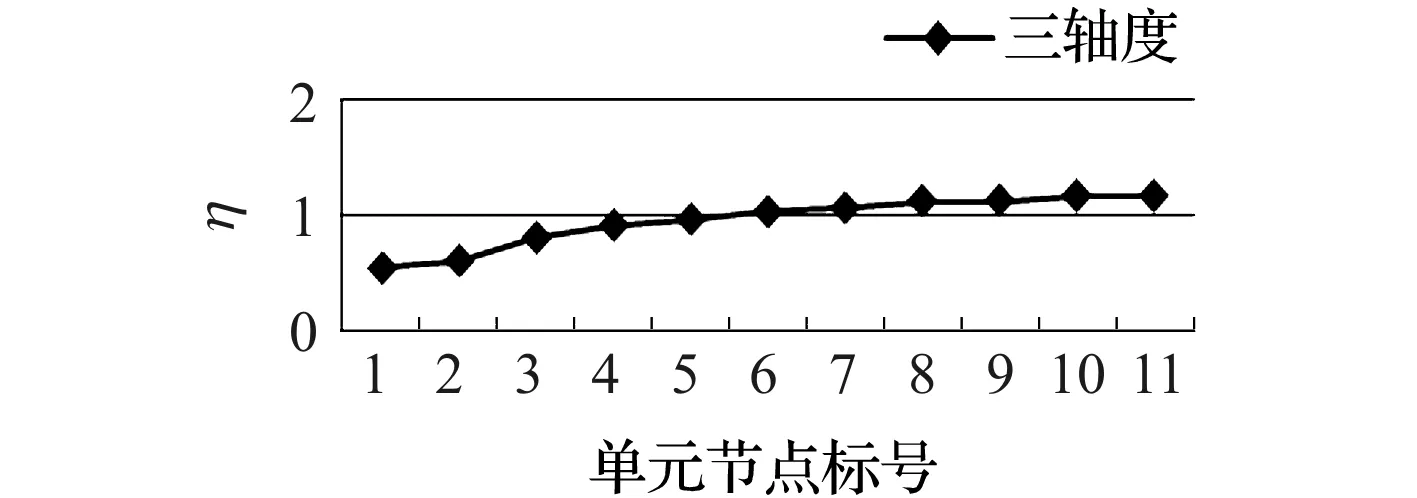
圖3 曲軸應力狀態分布

圖3中，MISE表示曲軸有限元模型節點的Von Mises等效應力，MAX、MID和MIN分別表示3個主應力，H表示靜水壓力，橫坐標表示單元節點標號。

2 圓形缺口件的優選設計

2.1 圓形缺口件的尺寸參數

根據力學理論，對于由同等材料制成的實際構件與缺口件，在受力狀態與載荷變化歷程相同的前提下，二者的疲勞損傷過程理論上應該是一致的。因此通過設計并選擇合適形式的缺口件，使其在載荷作用下的受力狀態與變化歷程與實際構件一致，便可實現標準缺口件與實際構件的等效。

依據這一理論，可設計圓形缺口件，結構如圖4所示。

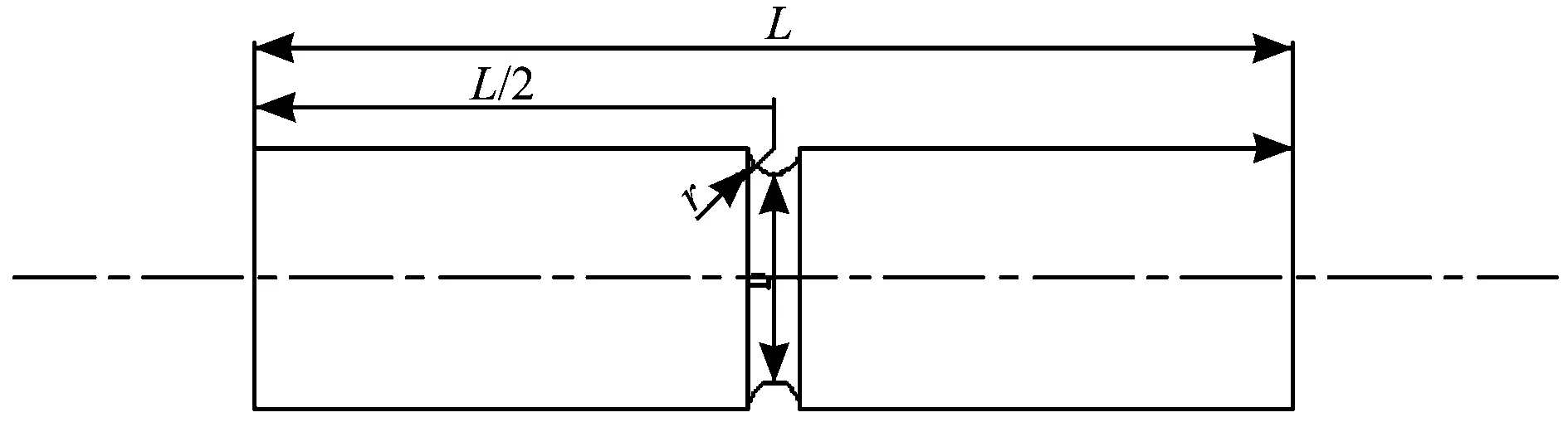
圖4 圓形缺口件結構示意圖

圓形缺口件的結構尺寸參數包括缺口件長度L，缺口件直徑d以及缺口半徑r，其中d=43 mm，與曲軸裂紋擴展的路徑長度一致。

2.2 圓形缺口件的有限元及受力狀態分析

本研究選取d=43 mm，r=10 mm，L=200 mm(該尺寸是試驗臺能夠可靠裝夾缺口件的最小長度)，對圓形缺口件進行不同長度下的有限元計算，載荷為作用在缺口件上表面的對稱彎矩，大小為1 000 N·m。

邊界條件為約束缺口件底面的所有自由度和對稱截面的平移自由度，計算結果如表2所示。

表2 圓形缺口件應力狀態的變化

注：表中各參數含義與表1的相同，其載荷特征為r=-1

2.3 圓形缺口件的尺寸參數對應力分布的影響

2.3.1 圓形缺口件長度L對應力分布的影響

本研究選取d=43 mm，r=10 mm的圓形缺口件，對其進行不同長度下的有限元計算，載荷為作用在缺口件的上表面的彎矩，大小為1 000 N·m，邊界條件為約束缺口件底面的所有自由度和對稱截面的平移自由度，圓形缺口件應力分布計算結果如圖5所示。

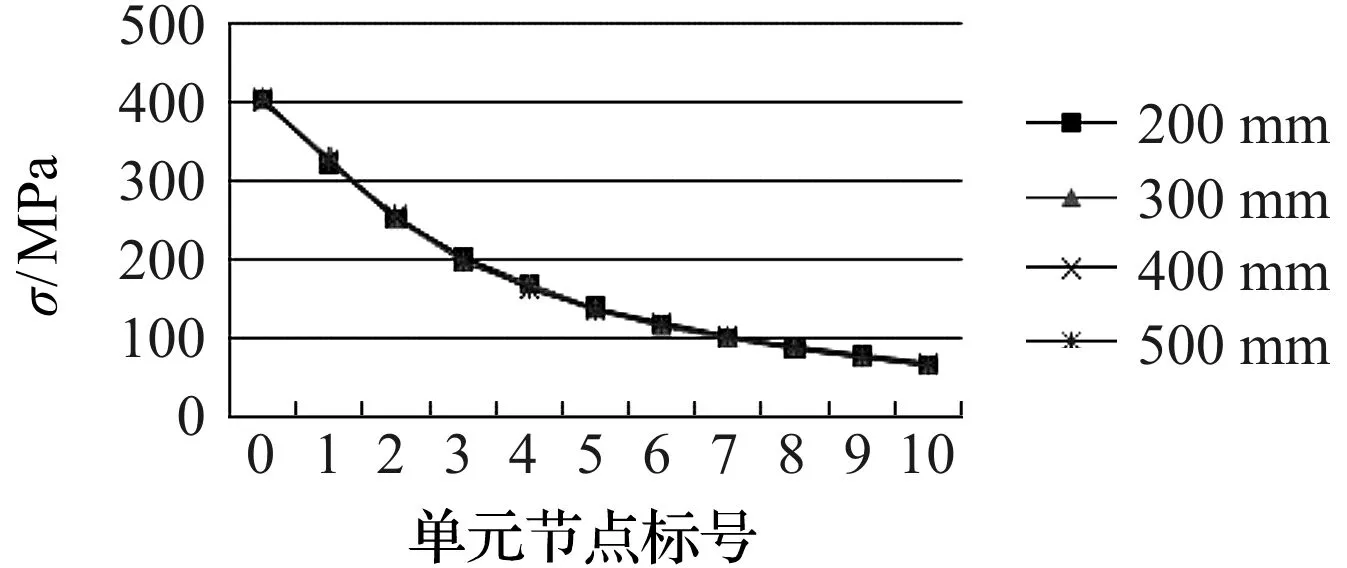
圖5 不同長度下的圓形缺口件應力分布

由圖5可知：在保持圓形缺口件的直徑和缺口半徑以及載荷大小不變的情況下，單獨改變缺口件的長度，對缺口件應力分布幾乎沒有影響。因此，本研究在后續的缺口件優選過程中，不再將缺口件長度作為改變參數，而是統一定為200 mm。

2.3.2 圓形缺口件缺口半徑r對應力分布的影響

本研究取L=200 mm，d=43 mm的缺口件，對其進行不同缺口半徑下的有限元計算。為了能夠更準確地進行對比，調整各尺寸下缺口件所受載荷值，使其最大應力與曲軸最大應力相同，觀察期應力變化梯度，結果如圖6所示。

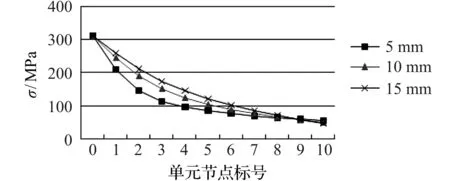
圖6 不同半徑下的圓形缺口件應力分布

由圖6可以看出：當缺口件的缺口半徑增大時，應力下降的梯度變小。

2.4 圓形缺口件的優選設計方法

在缺口件和曲軸的疲勞損傷過程中，隨著裂紋的擴展，其內部的應力狀態也將發生相應的變化，通過改變缺口件的缺口半徑，構造與曲軸的應力狀態最為接近的缺口件，最優解的選擇方法為同一距離點的兩應力差值百分比之和D最小，即：

(3)

式中：σin—曲軸在該深度下的Von Mises等效應力；σic—缺口件在該深度下的Von Mises等效應力。

經計算得到該尺寸的缺口件與曲軸之間的D值為0.717 5。二者的應力梯度及應力狀態對比如圖(7，8)所示。

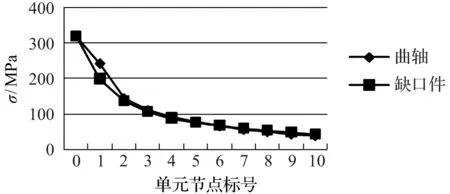
圖7 曲軸與圓形缺口件應力梯度分布

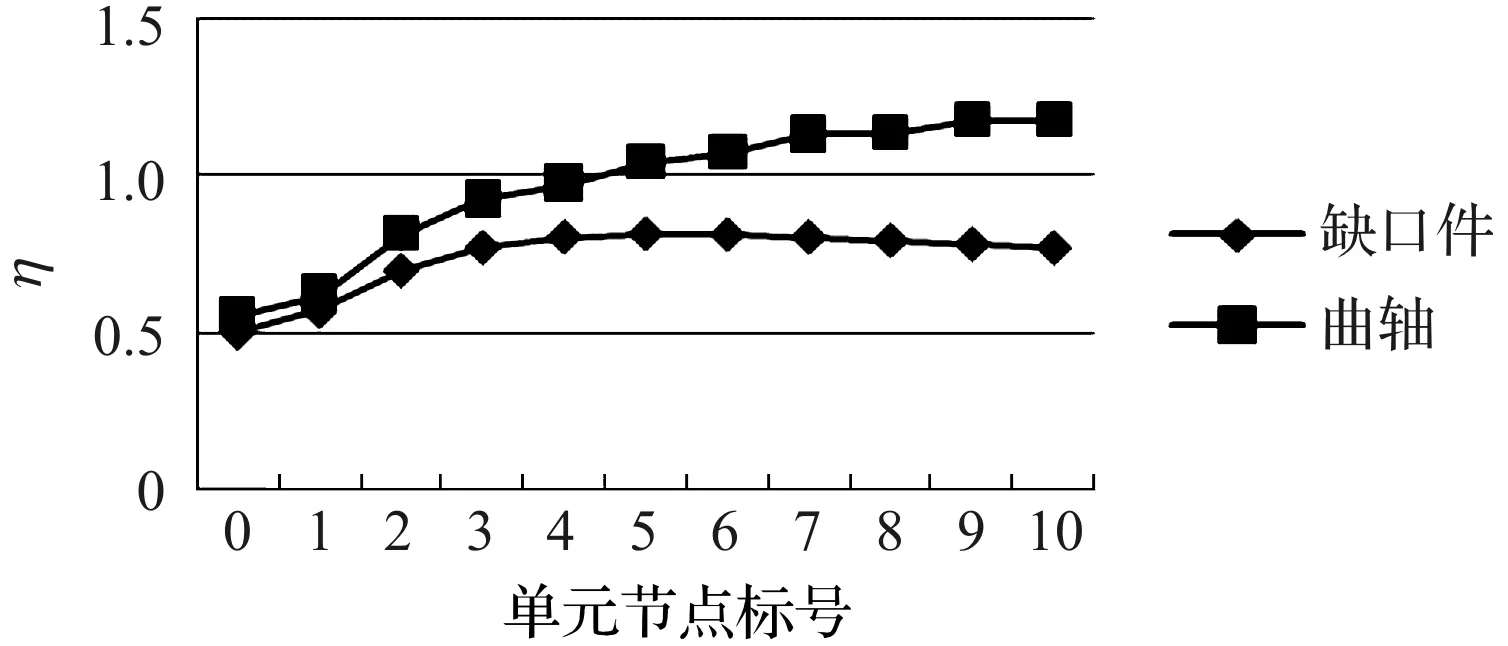
圖8 曲軸與圓形缺口件應力狀態對比

3 橢圓形缺口件的優選設計

3.1 橢圓形缺口件的尺寸參數

橢圓形缺口件的結構尺寸參數包括缺口件長度L，缺口件直徑d以及缺口的長軸半徑a以及短軸半徑b。

橢圓缺口件結構示意圖如圖9所示。

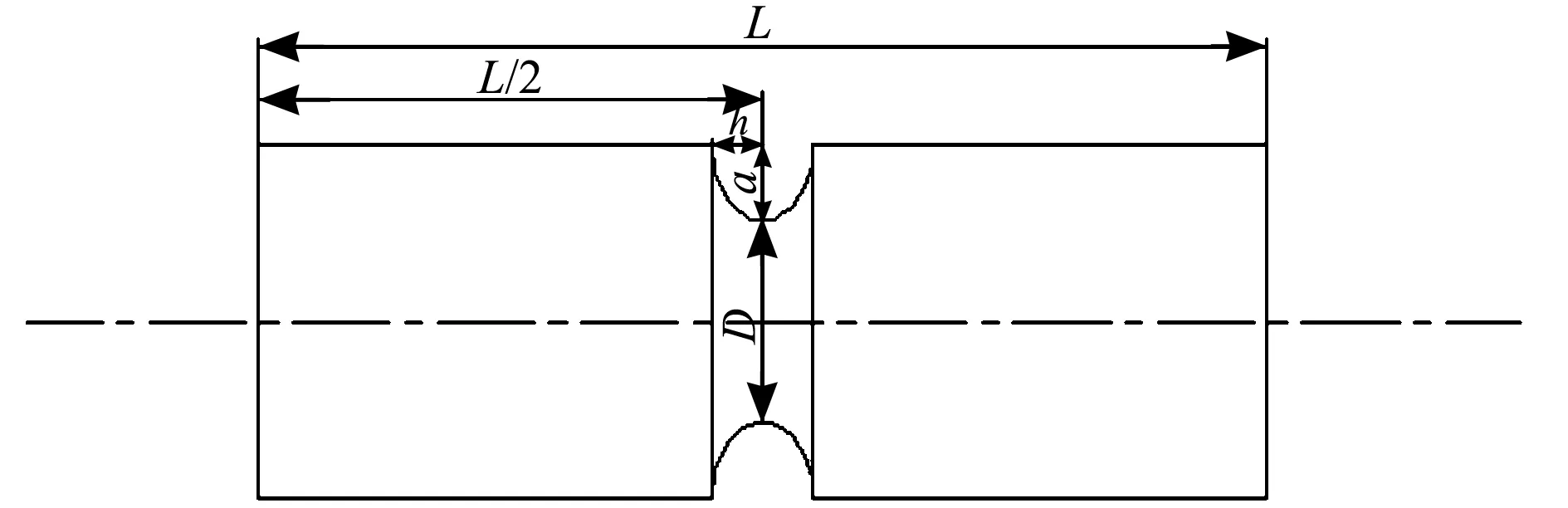
圖9 橢圓缺口件結構示意圖

3.2 橢圓形缺口件的有限元及受力狀態分析

本研究選d=43 mm，a=10 mm，b=5 mm，L=200 mm的橢圓形缺口件，對其進行不同長度下的有限元計算，載荷為作用在缺口件的上表面的對稱彎矩，大小為1 000 N·m。

邊界條件為約束缺口件底面的所有自由度和對稱截面的平移自由度，計算結果如表3所示。

3.3 橢圓形缺口件的尺寸參數對應力分布的影響

3.3.1 橢圓形缺口件長度L對應力分布的影響

本研究選取a=10 mm，b=5 mm的橢圓形缺口件，對其進行不同長度下的有限元計算，載荷為作用在缺口件的上表面的彎矩，大小為1 000 N·m，邊界條件為約束缺口件底面的所有自由度和對稱截面的平移自由度。計算結果與圓形缺口件的相同，即在保持橢圓形缺口件的長、短軸以及載荷大小不變的情況下，單獨改變缺口件的長度，對缺口件應力分布幾乎沒有影響。因此，在后續的缺口件優選過程中，不再將缺口件長度作為改變參數，而是統一定為200 mm。

注：表中各參數含義與表1的相同，其載荷特征為r=-1

3.3.2 橢圓形缺口件短軸b對應力分布的影響

本研究選取a=10 mm，d=43 mm，L=200 mm的橢圓形缺口件，對其進行不同短軸下的有限元計算，載荷為作用在缺口件的上表面的彎矩。

為了能夠更準確地對比，本研究調整各尺寸下缺口件所受載荷值，使其最大應力與曲軸最大應力相同，計算結果如圖10所示。

由圖10可以看出：當橢圓形缺口件的短軸增大時，應力下降的梯度變小，這是因為隨著橢圓缺口件的短軸長度的增加，缺口的應力集中系數變小。

3.3.3 橢圓形缺口件長軸a對應力分布的影響

本研究選取b=5 mm，d=43 mm，L=200 mm的橢圓形缺口件，對其進行不同長軸下的有限元計算，載荷為作用在缺口件的上表面的彎矩，為了能夠更準確地對比，本研究調整各尺寸下缺口件所受載荷值，使其最大應力與曲軸最大應力相同，計算結果如圖11所示。

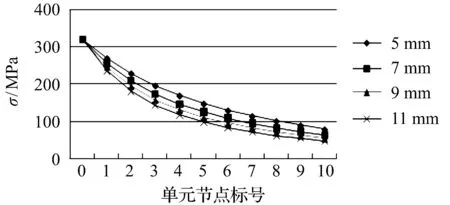
圖11 橢圓缺口件應力分布隨長軸變化

由圖11可以看出：當缺口件的長軸增大時，應力下降的梯度變大，這是因為隨著橢圓缺口件長軸的增長，缺口的應力集中系數變大。

3.4 橢圓形缺口件的優選設計結果

綜上所述，對于橢圓形缺口件，在缺口件直徑一定(d=43 mm)的情況下，本研究以橢圓形缺口件的長、短軸為變量，進行不同尺寸缺口件的有限元模型構造，并對計算結果進行優選，使得缺口件的應力梯度與曲軸誤差最小，最后求得缺口件的缺口尺寸參數為a=15 mm，b=10 mm。

橢圓形缺口件與曲軸的應力梯度及應力狀態對比如圖(12，13)所示。

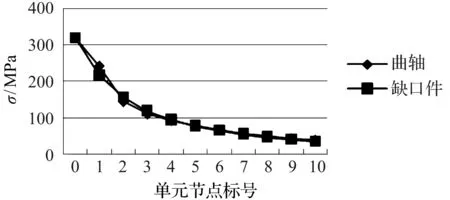
圖12 曲軸與橢圓形缺口件應力梯度分布

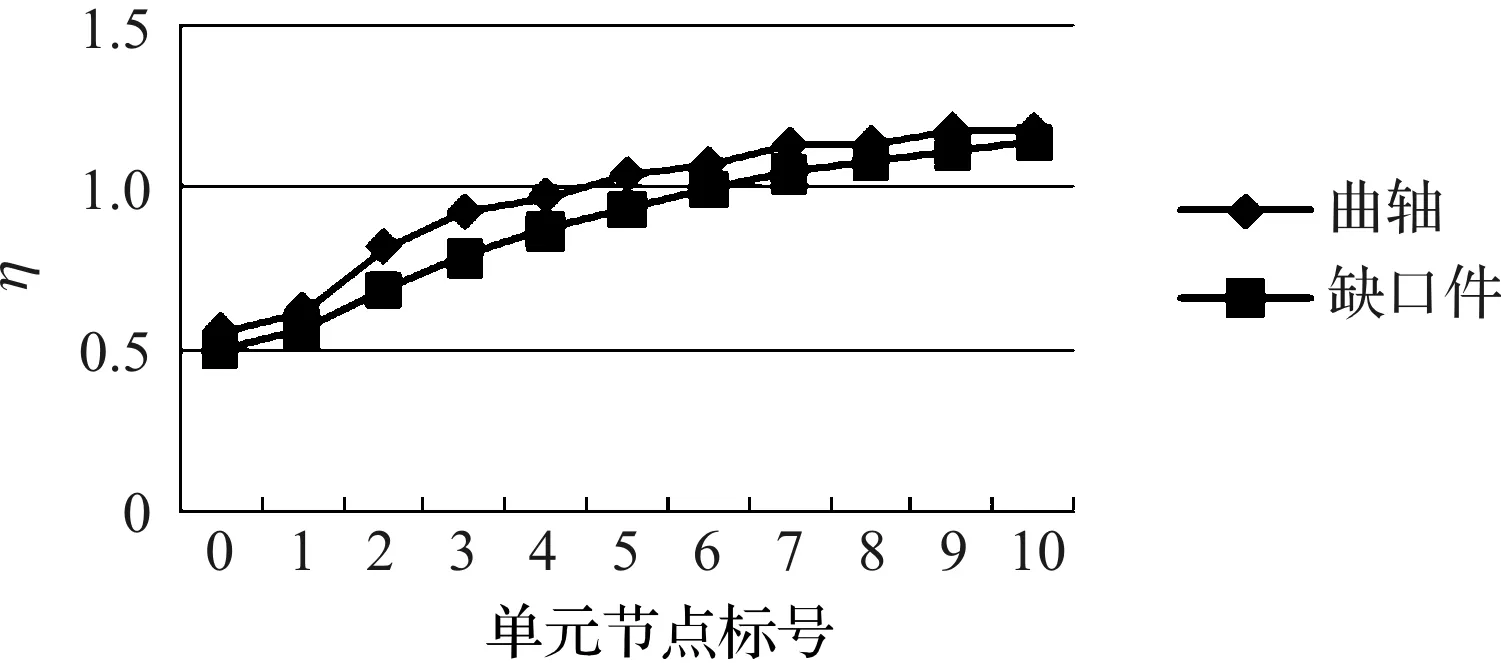
圖13 曲軸與橢圓形缺口件應力狀態對比

當a=15 mm，b=10 mm時，經公式(3)計算得到該尺寸下的缺口件與曲軸的D值為0.517。通過對比可以發現相比較圓形缺口件，橢圓形缺口件無論是應力梯度還是應力狀態，都比圓形缺口件更加接近實際的曲軸。

4 實驗及結果分析

在曲軸彎曲疲勞試驗中，通過由電機、偏心輪、主動臂、從動臂組成的加載系統，對曲軸進行對稱載荷加載，以模擬曲軸實際工況中的疲勞損傷過程。當曲軸在疲勞加載過程中出現裂紋萌生和擴展，曲軸的剛度逐漸下降，響應加速度逐漸變大，系統通過反饋控制降低電機的轉速，以保持對曲軸的恒幅加載。當電機轉速下降到一定值之后，就認為曲軸失效。

曲軸為非對稱結構，在對稱載荷作用下的疲勞損傷過程中，裂紋的萌生以及擴展，都只出現在連桿軸頸的圓角結構處；而缺口件為對稱結構，在對稱載荷作用下，理論上缺口件的兩側缺口都將出現裂紋，且以同樣的速率進行擴展。但在實際試驗當中，由于制造誤差以及缺口件內部缺陷等客觀因素的影響，缺口件很難做到兩側缺口的完全對稱疲勞，直接通過對比缺口件和曲軸的試驗結果并不可行。

通過前期討論及驗證，本研究決定采取間接驗證法，具體步驟如圖14所示。

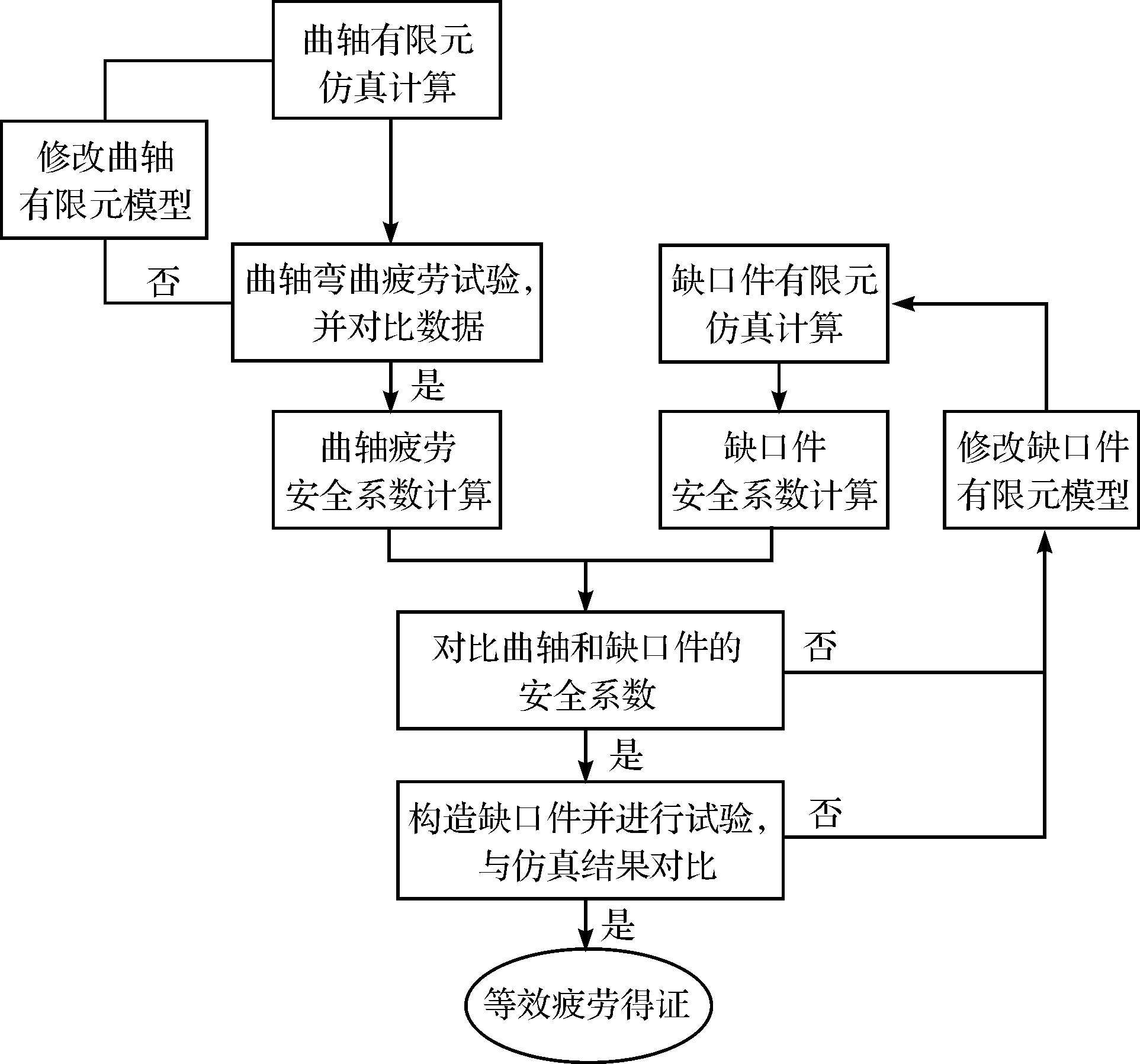
圖14 等效疲勞間接驗證流程

具體流程為：

(1)利用有限元法，確定缺口件的最終結構尺寸，并構造缺口件；

(2)針對缺口件和曲軸所受到的對稱載荷，進行疲勞損傷仿真計算，得到各自應力集中處的安全系數，并進行對比；

(3)對曲軸進行對稱載荷下的加載試驗，測得曲軸應力集中處的應力(或者應變、固有頻率)，與缺口件有限元結果進行對比。

通過驗證之前有限元計算的準確性，間接證明利用缺口件進行曲軸疲勞分析的可行性。

橢圓形缺口件有限元仿真及曲軸疲勞試驗結果對比如表4所示。

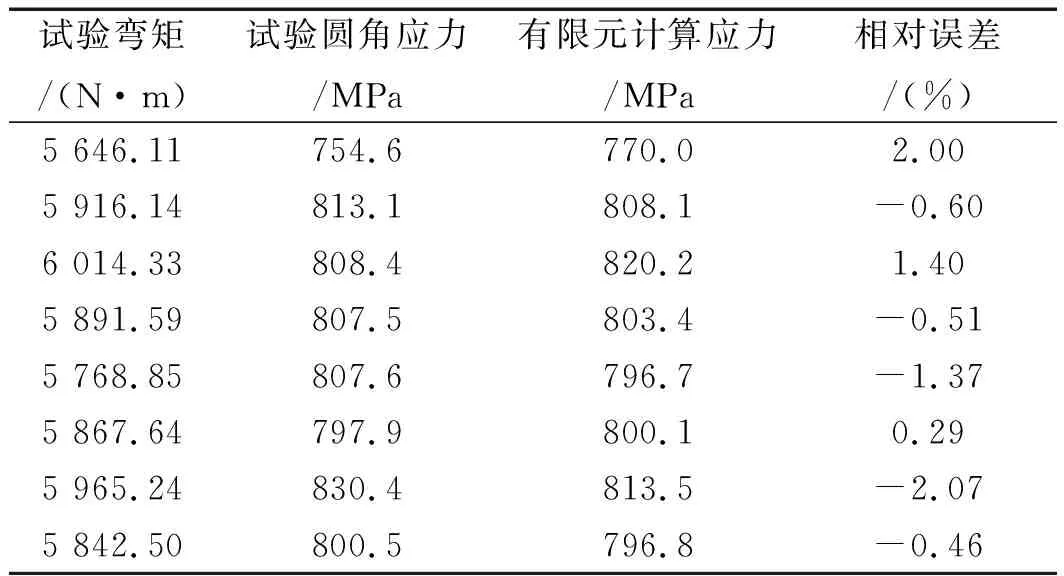
表4 橢圓形缺口件有限元仿真及曲軸疲勞試驗結果對比

由表4可以看出：不同彎矩下兩者得到的曲軸圓角應力的最大誤差小于2.07%，驗證了兩者的疲勞等效性。

5 結束語

本研究采用有限元分析的手段得到某一型號曲軸的受力狀態，并以該曲軸為基礎，分別設計了該曲軸的圓形和橢圓形缺口件，在對比分析了兩者的尺寸參數對應力分布和應力梯度分布的影響的基礎上，提出了缺口件的優選設計方法和流程。

研究結果表明：橢圓形缺口件無論是在應力狀態還是在應力梯度方面都比圓形缺口件的等效精度更高，更接近實際曲軸結構。對橢圓形缺口件的有限元計算結果和曲軸疲勞試驗結果得到的圓角應力進行了對比分析，結果表明兩者的最大誤差小于2.07%，從而驗證了應用橢圓形缺口件進行曲軸疲勞分析的可行性。