基于免疫優化的腦電自適應集成分類方法研究*

李嘉偉，任立紅，丁永生，陳 磊

(東華大學 數字化紡織服裝技術教育部工程研究中心，上海 201620)

0 引 言

近年來，基于腦電(electroencephalogram, EEG)信號的腦機接口系統受到了廣泛的關注。腦機接口是一種新的人機交互方式，通過識別腦電信號來獲取被試者意圖，這項技術能為神經肌肉損傷的患者提供不依賴外圍神經的新的通訊工具[1]。通常在EEG信號處理中，P300誘發電位由于它的穩定性，以及不需要訓練等特性越來越被研究人員所接受。P300誘發電位是一種事件相關電位[2]，是對發生概率相對較小的外界事件或刺激的反應，由于P300誘發電位一般出現在刺激發生后300 ms左右，故稱為P300信號。

基于腦電信號識別用戶意圖是腦機接口的核心任務，特征提取和分類是識別腦電信號最重要的環節，直接決定了分類的性能。目前特征提取以及分類算法主要分為3大類:生成模型分類器、線性分類器以及非線性分類器。在生成模型分類器中貝葉斯分類器是選擇具有最大后驗概率的類作為該對象所屬的一類。線性分類器中常用的是LDA(linear discriminant analysis)分類器，LDA分類速度快且無須高性能計算，通常用于二分類問題，在線性分類中占有一席之地[3]。另外一類是非線性分類器，例如支持向量機(SVM)神經網絡分類器等。RAKOTOMAMONJY A等[4]提出一種集成支持向量機，將數據分為多個類，并利用不同的支持向量機訓練數據，最后綜合多個支持向量機的結果來降低由于單個數據誤差造成的整體影響，并最終得出96%的分類準確率；CECOTTI H等[5]將卷積神經網絡(CNN)應用于腦電分類中，提出了基于CNN的7個分類器—4個具有不同特征集的單一分類器以及3個多分類器，并應用于BCI競賽數據集得出95.5%的識別率；除此之外還有多種用于分類的方法如基于小波變換的識別算法[6-7]、線性回歸算法[8]。

在近幾年腦電最新研究成果中，國內學者利用SSVEP信號針對以往只控制機器人方向的實驗進行改進[9]，加入了對機器人速度的精細化控制，結果表明：通過對設備的恰當設置，8名被試腦控機器人到達終點平均用時2分40秒，能夠實現對機器人多個運動方向和多級速度控制；孟明等[10]學者在處理運動想象腦機接口中引入堆疊降噪自編碼器提出一種兩級特征提取方法應用于BCI VI的數據，平均Kappa系數可以達到0.69。除此之外，國外的一些學者針對腦電的高度非平穩性，以及傳統靜態方法在線應用識別錯誤率高的問題，在自適應分類算法上做出研究，可以實時更新分類器參數，例如VIDAURRE C等[11]提出一種簡單的無監督自適應LDA分類器，可以抵消腦電信號非平穩性的負面影響，并且將算法應用于在線實驗其性能甚至優于目前最先進的監督學習算法。

本文將結合SVM的二分類性能以及IA算法的自適應性，提出基于IA的自適應集成算法。

1 基于免疫優化的混合核函數集成SVM

1.1 Bagging集成學習方法

單一SVM分類準確率低，所以本文借用了集成學習方法的思想[12]。集成學習方法中AdaBoost算法主要用于弱分類器，對于腦電這種高維小樣本信號分類不理想，所以采用Bagging集成算法，對強分類器進行集成。Bagging算法對訓練樣本進行采樣，之后訓練出n個相互獨立的強學習器。在對預測輸出進行結合時，對分類任務通常采用簡單投票法。

1.2 IA-SVM算法

1.2.1 SVM算法

SVM是建立在統計學習理論、VC維理論和結構風險最小化原理基礎上的機器學習方法，它在解決小樣本、非線性和高維模式識別問題中有優勢。

給定一個數據集T以及n個樣本，T={(xi,yi),i=1,…,n,xi∈Rd,yi∈{-1,+1}}。其中：xi—輸入集；yi—目標值。

數據集x經過非線性變換φ(x)可以映射到高維空間F：

φ:Rn→F
x→X=φ(x)

(1)

線性回歸函數f(φ(x))可以在空間F中預測目標y的值：

(2)

式中：w—權值向量，w∈F；b—偏移量。

式(2)即為F中的超平面，在超平面確定的情況下，根據結構風險最小化原理可以從中找出間隔最短的最優超平面，即：

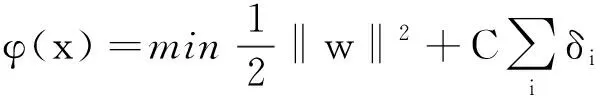
(3)

式中：C—正規化參數，其取值范圍較大，該類型的SVM稱為C-SVM。

只要采取適當的內積函數φ(xi)就可以實現某一非線性變換后的線性分類，而計算復雜度沒有增加。將正定的核函數k(x,xi)代替點乘x·xi，分類器的判別函數轉化為：

(4)

常用的內積函數有兩種。一種為多項式核函數:K(x,xi)=[r*(x·xi)+coef]d。其中：d—多項式的階；coef—偏置系數。多項式核函數是全局性核函數中的典型代表，其最突出的特點是泛化能力強。另一種為高斯核函數(RBF)。K(x,xi)=exp(-r*‖x-xi‖2)。其中：r—核函數的寬度。高斯核函數是局部性核函數的代表，對一定距離內的樣本具有很好的學習性能。

1.2.2IA算法

智能算法是受生物自然機理啟發而得出的一系列處理策略，如人工免疫算法、遺傳算法以及粒子群算法[13-18]。人工免疫算法是在免疫學理論基礎上發展起來的一種新興的智能算法。通常，免疫算法的優化策略如下：

(1)生成初始群體。將數據輸入，如果記憶庫非空，則初始抗體群從記憶庫中選擇生成。否則在可行解空間隨機產生初始抗體群，滿足約束條件：

β∈{0,1},β,θ,∈{0,10}

(5)

(2)對上述群體中各抗體進行評價。通常對個體評價是以個體期望繁殖率P為標準的；在群體中，每個個體的期望繁殖率由抗體抗原間親和力AV和抗體濃度CV兩部分共同決定：

(6)

通過式(6)可得出當前SVM種群分類錯誤率。抗體濃度CV為群體中相似抗體所占比例：

(7)

式中：kυ,s—抗體v與抗體s相同位數；L—抗體長度；N—抗體總數。

根據AV，CV可得出當前抗體期望繁殖率。

(3)形成父代群，更新記憶庫。將初始群體按期望繁殖率P進行降序排序，并取前N個個體構成父代群，同時取前m個個體存入記憶庫中；

(4)判斷是否滿足結束條件，是則結束，反之則繼續下一步；

(5)新群體產生。基于步驟(3)的計算結果對抗體進行選擇，pc概率交叉，pm概率進行變異得到新群體，再從記憶庫中取出記憶個體，共同構成新一代群體；

(6)轉去執行步驟(2)。

1.2.3 IA-SVM算法

通過上文對兩種算法的介紹，SVM的性能取決于它的參數、內核以及C參數，然而對于不同的內核，C的選擇也不同，SVM參數需要根據實際數據的不同特征來選擇，例如腦電分類中每個個體腦電特征都會存在細微差別，固定的SVM參數不能很好地適應每個個體。這個問題利用目前先進的免疫算法可以很好地解決，借鑒免疫算法產生多樣抗體的能力，以及免疫系統的自我調節機構和免疫記憶功能。免疫算法是一種自適應智能算法，可以針對SVM對不同個體參數的不確定性進行優化。將SVM與免疫算法結合出自適應的分類算法，把參數作為初始種群輸入免疫算法中，通過種群間個體信息交換，新種群產生這一循環過程來獲得問題最優解，每一代種群中借助克隆選擇，免疫記憶，疫苗接種等機理可以保存下來優秀的參數，并且又保證了參數的多樣性。本文通過對SVM以及IA兩種算法的結合利用IA的自適應性優化SVM強大的二分類性能從而可以對腦電信號進行分類得出較高的分類準確率。

IA-SVM完整流程圖如圖1所示。

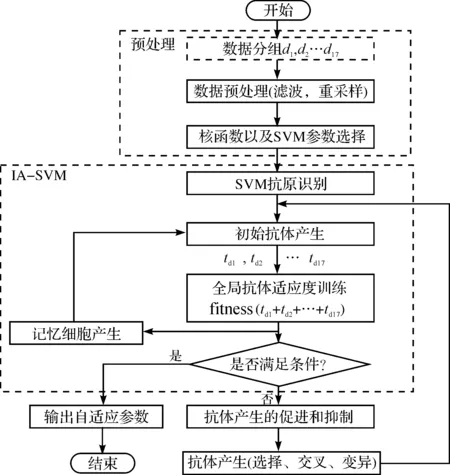
圖1 整體算法流程圖

IA-SVM算法中將SVM中需要的參數看作是免疫算法中的抗原，每次迭代存儲下來這一代優秀的參數作為記憶細胞，并對最終SVM分類結果進行優化。

2 腦電信號分類的應用

2.1 數據集

本文實驗所用EEG數據來源于BCI Competition III Dataset II所提供的P300拼寫器實驗數據[16]。該P300拼寫器基于Oddball范式，是利用P300誘發電位即視覺刺激后約300 ms開始在頭頂皮層引起的EEG正峰設計出的BCI應用實驗，實驗所用EEG數據如圖2所示。

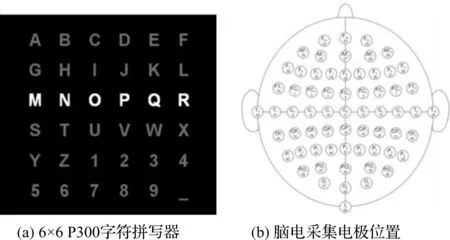
圖2 實驗所用EEG數據

該拼寫器實驗由FARWELL和DONCHIN[17]在1988年提出，是一個6×6的字符矩陣。Oddball拼寫器實驗設計如下：拼寫器的6行6列會隨機被高亮，被試者需要從拼寫器的36個字符中選出一個字符作為靶目標，然后全神貫注地觀察高亮的行或列中是否存在靶目標。根據伏云發等[18]對腦信號時間-空間模式的定義:

(8)

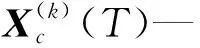
對于Oddball實驗6行6列各隨機高亮一次稱為一次Trail，即每次Trail對應12次高亮，為了使試驗數據更可靠，被試者在選定一個字符后要進行15次這樣的重復Trail實驗，每次需要對靶目標所在行和列的高亮次數進行計數，這樣靶目標的高亮次數對于非靶目標來說就是小概率事件(分別為2次高亮和10次高亮)，可以誘導被試者產生P300信號。根據這一特點，均出現P300電位的行與列交叉得到的字符就是被試者注視的字符。

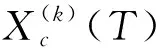
(9)

式中：ED(Error decision)—錯誤決策數目；CD(Correct decision)—正確決策數目。

2.2 數據預處理

P300與非P300信號對比如圖3所示。

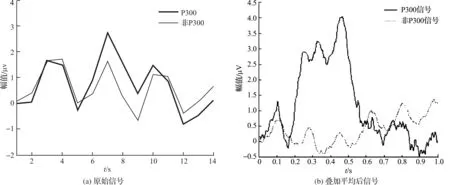
圖3 含P300與不含P300信號對比

從原始信號中含P300與不含P300信號對比中可以看出：在6 s～8 s時間區間內P300信號幅值要略大于非P300信號，但是圖中現象不夠明顯，可以通過取平均操作來降低信號信噪比從而看出P300與普通信號差別。將多組P300與非P300信號疊加取平均后效果非常明顯，可以看出包含P300腦電信號的幅值遠遠大于非P300腦電信號。

P300誘發電位通常出現在受刺激后300 ms時間范圍內，所以本文采取刺激后0～667 ms時間點的電位值，從文獻中可以得出P300誘發電位是低頻波，所以低通濾波和下采樣可以去除高頻成分中的不重要的信息。對每一個提取出來的信號通過8階帶通截止頻率0.1 Hz～10 Hz的Chebyshev Type I濾波器，之后再對信號根據最高頻率進行下采樣，通過以上預處理步驟后得到待分類的腦電輸入信號。

2.3 參數以及分類器選擇

首先需要確定集成算法中基分類器的個數，查閱文獻得知腦電數據采集時有很大的時間相關度，即被試者在短時間內腦電數據處于一個狀態，根據這方面考慮決定對樣本采用時間序列分組，按照樣本的采樣時間順序，1～5組數據訓練一個基學習器，6～10位一個基學習器，以此類推訓練得出17個基學習器。

之后確定基學習器，本次實驗為二分類問題，所以本研究選擇一些常用分類方法作為對比試驗。針對實驗腦電數據Dataset II，在不使用集成分類以及免疫優化的條件下分別測試SVM、神經網絡、稀疏自編碼器(sparse auto encoder, SAE)、深度信念網絡(deep belief networks, DBN)4種分類器下10次測試平均分類錯誤率，實驗結果如表1所示。

表1 分類器對比結果

結果顯示：直接對預處理過后腦電信號進行二分類，SVM效果最佳，平均分類錯誤率僅為0.116 2，優于其他3種分類器。在神經網絡分類器中稀疏自編碼器與深度置信網絡效果相近，神經網絡稍差。從實驗結果可以看出采用SVM作為基分類器可以達到更好的分類效果。同時也得出不使用集成分類以及免疫優化時最佳分類準確率僅能達到0.92，對腦電信號的分類準確度并不高。

2.4 實驗及結果分析

訓練好所有基學習器后，對被試者的測試數據利用集成的自適應分類算法進行分類。經過實驗不同免疫迭代次數下該算法對測試數據的字符識別結果，正確字符集，以及識別正確率如表2所示。

從表中識別結果可以看出:算法對識別字符率的優化效果，識別準確率隨著迭代次數增加逐步提高。在迭代次數達到13時，獲得0.96的準確率，已與競賽第一準確率持平，在迭代次數達到15時，獲得最高98%的準確率。

表2 不同免疫算法迭代次數正確率

免疫算法對參數優化效果如圖4所示。

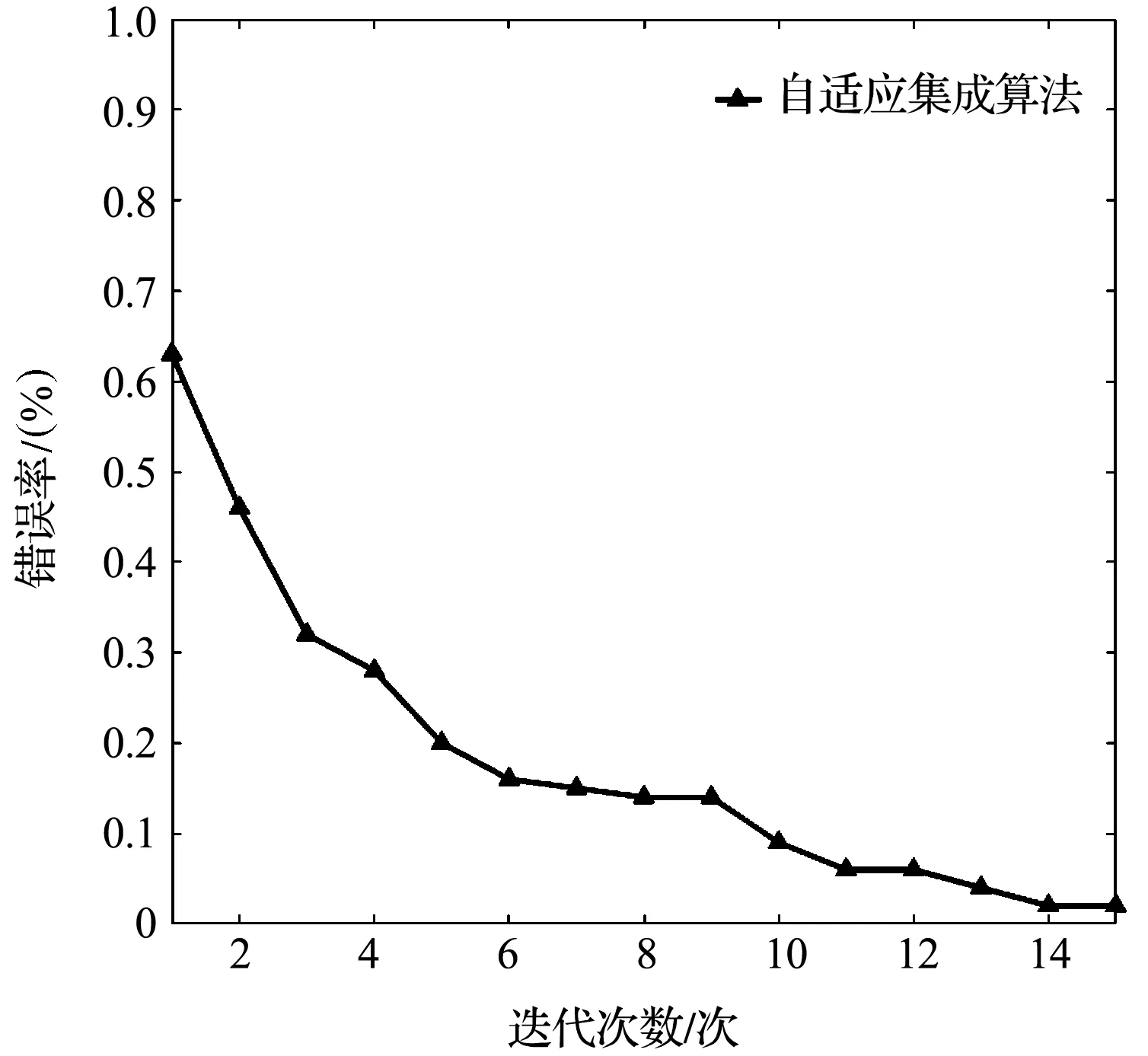
圖4 免疫算法對支持向量機優化效果

圖4展示了免疫算法迭代次數不斷增加對17個支持向量機參數的優化結果。可以看出參數隨著迭代次數的增加使整體朝著錯誤率低的方向自適應地改變，并逐漸趨于穩定。

為了更直觀的表達本文方法在腦電分類上的優良性能，還進一步對比分析在兩個不同被試者(Dataset I, Dataset II)試驗集上不同優化方法的分類準確率。

本文算法在兩個數據集上與未使用自適應集成算法以及PSO優化算法的分類正確率對比如圖5所示。

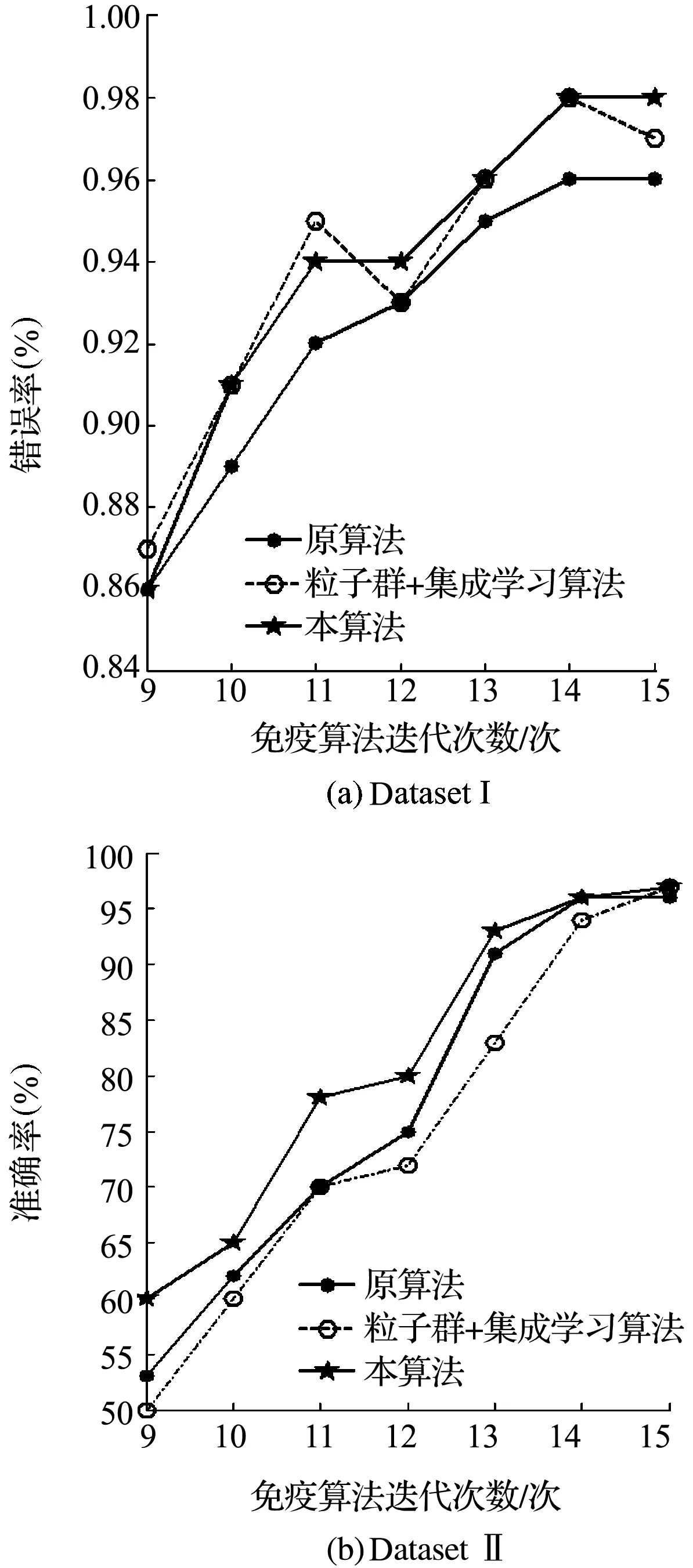
圖5 自適應集成學習算法與原始分類算法以及PSO優化算法對比

PSO是一種基于群體的算法，是一種與免疫算法類似的優化算法。PSO算法粒子速度及位置更新公式如下：

(10)

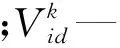
PSO算法中，粒子速度可以智能地隨著局部以及全局最優解更新來調控最終結果，從而得出結果最佳的參數。接下來對比分析3種算法對數據集的分類效果，從dataset I可以看出PSO對參數優化可以提高準確率，然而缺點在于PSO不能保存優秀解，免疫算法迭代次數從11到12以及14到15均出現準確率下降，同樣對比原算法與自適應算法可以看出自適應參數與定值參數相比，自適應參數可以很好地調節準確率，迭代15次時可以達到0.98的準確率，比原準確率提高了0.2。且整體水平均高于原競賽第一名。在分析dataset II數據可以看出自適應算法的增長速度均高于其他兩種算法，證明其擁有很好的適應調節效果，最終準確率可以達到0.97。

綜合兩張圖，該算法都能獲得相對較優的準確度，表明該法在處理P300腦電信號這類問題上是可行性的。

3 結束語

本文提出了一種自適應的集成分類方法，該算法利用免疫算法對集成的SVM中每個基學習器進行尋優，最后得出98%的分類正確率；免疫優化算法可以保留優秀的參數，并且又保證了參數的多樣性，與集成的SVM結合，可以改進SVM參數，又通過適當的核函數選擇得到自適應的效果，使分類準確率達到最佳。

由于數據分組較多，本文提出的自適應的集成分類算法免疫優化的尋優過程需要一定的時間，準確率的提高以損失時間作為代價，所以該法適用于離線處理，對于在線的腦電處理還需進一步研究。