多元線性回歸的估值漂移及其判定方法

高 庚，吳 悠，葛永慧

（太原理工大學 礦業工程學院，太原 030024）

0 引言

在實際生產實踐和科學實驗中，為了闡明多種因素與事件發生、發展的關系，通常采用多元線性回歸分析的方法。多元線性回歸研究的是建立一個能反映因變量Y與多個自變量X之間線性關系的多元回歸方程，利用這個方程來分析因變量和自變量之間的相互關系，以及回歸系數的相關情況等。為了檢驗回歸方程的擬合程度，通常采用復相關系數和復判定系數來進行判定，復相關系數和復判定系數越趨近于1，說明因變量和自變量的線性關系越密切，回歸方程的擬合程度越高，回歸有效性越好。文獻[1]詳細敘述了最小二乘法(LS法)在多元線性回歸分析中的應用研究，以及相關系數等的計算。文獻[2]運用仿真實驗的方法，在多元線性回歸分析中，通過回歸系數估值的相對真誤差發現，在應用LS法解算多元線性回歸系數時，總會有回歸系數估值明顯偏離其真值的現象出現，即估值發生了顯著漂移。大量模擬實驗表明，即便復相關系數和復判定系數都趨近1，也總會有回歸系數發生估值漂移現象，甚至會發生嚴重的估值漂移。在多元回歸統計分析的分支中，如主成分分析、因子分析等，回歸系數的有效性顯得尤為重要，若其回歸系數發生了顯著估值漂移，則將會產生不可預知的結果。

本文以三元線性回歸分析為例，對回歸系數中出現的顯著估值漂移現象進行了分析與討論，并進一步通過二元至五元線性回歸仿真實驗，提出了一種判定多元線性回歸系數估值漂移的總體指標和判定回歸系數有效性的基本條件。

1 材料與方法

1.1 多元線性回歸的計算

多元線性回歸方程的一般形式：

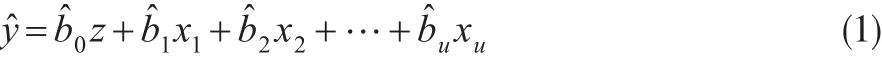
誤差方程：

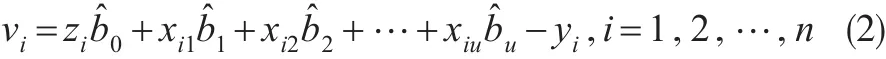
由LS法得多元線性回歸的法方程：

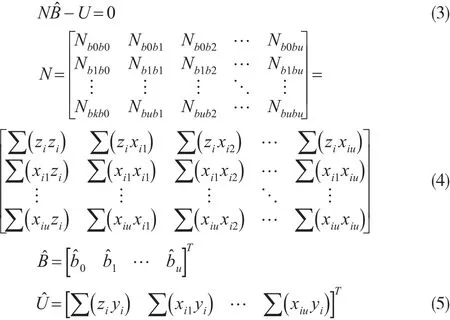
式中，N為法方程系數矩陣，Q為協因數矩陣。

回歸系數的解：

觀測值的均方誤差：

觀測值絕對值平均值：

相關系數、復相關系數和復判定系數：

1.2 參數估值的相對真誤差與估值漂移

定義：用參數估計方法得到的參數的估值顯著地偏離其真值的現象稱為參數的估值漂移（Estimated Value Drift，EVD）。當dk＞時就認為是“估值顯著地偏離其真值”。不同應用可對賦予不同值。當dk＞=50%時，參數估值的有效數字只有1位，而且還是可疑數字，稱為參數具有顯著估值漂移。dk表示觀測值估值的相對真誤差或回歸系數估值的相對真誤差。

實踐表明，在多元線性回歸分析中，當觀測值母體的均方誤差大到一定程度，回歸系數估值就可能出現估值漂移現象。用σ0表示觀測值母體的均方誤差，||表示參與回歸計算的觀測值絕對值的平均值，ω表示為均方誤差系數。對于給定的估值漂移指標，當：

就認為回歸系數估值可能產生估值漂移。在實際應用中用觀測值的驗后均方誤差?0代替觀測值母體的均方誤差σ0。

2 結果與討論

2.1 算例

三元線性回歸的理論回歸方程：

用觀測值真值加隨機誤差生成三組模擬觀測值（簡稱為觀測值），三元線性回歸的理論觀測值與模擬觀測值見表1。對于三組模擬觀測值分別用LS法計算回歸方程回歸系數估值、相對真誤差及相關系數見表2。

2.1.1 回歸系數估值可能產生估值漂移

表1 三元線性回歸的理論觀測值和模擬觀測值

表2 回歸系數估值、相對真誤差及相關系數

回歸數學模型的特點導致了回歸系數估值可能產生顯著的估值漂移。由于多元線性回歸數學模型的特點，導致了用LS法求解時法方程系數間的差異很大，例如在本算例中法方程系數主對角線Nb0b0=10.000、Nb1b1=1.272×1010、Nb2b2=1.808×108和 Nb3b3=2.871×109。不同的觀測值誤差會導致法方程的常數項有微小的變化，法方程的常數項的微小變化就有可能導致回歸系數的顯著變化。

觀測值估值不會產生顯著估值漂移。由后文表3可知，A、B和C三組的觀測值估值的相對真誤差最大值分別為0.59%、0.29%和0.06%，三組觀測值估值與其真值的差異均不顯著。

2.1.2 僅用復相關系數和復判定系數說明多元線性回歸的有效性有一定局限性

2.2 仿真實驗

理論觀測值模擬值見表1，仿真實驗方法見文獻[1]。理論觀測值絕對值的平均值約為1500。回歸系數估值相對真誤差均小于等于給定限值的百分比見表3。回歸系數估值相對真誤差平均值和相對均方誤差平均值的百分比見表4。

表3 回歸系數估值相對真誤差均小于等于的百分比（%）

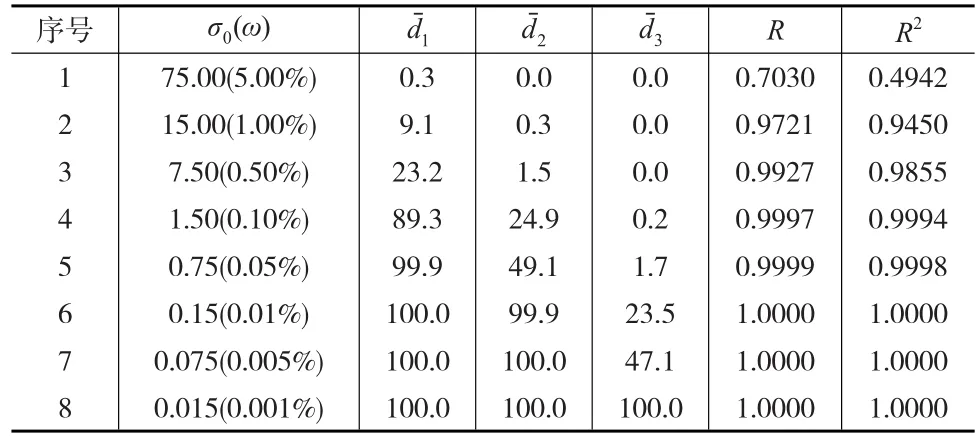
表3 回歸系數估值相對真誤差均小于等于的百分比（%）

注：σ0表示觀測值母體均方誤差，ω表示均方誤差系數；1表示回歸系數估值的相對真誤差均小于等于=50%的百分比，2表示回歸系數估值的相對真誤差均小于等于=10%的百分比，表示回歸系數估值的相對真誤差均小于等于=1%的百分比。R表示復相關系數的總體平均值，R2表示復判定系數的總體平均值。

序號1 2 3 R R2 0.4942 0.9450 0.9855 0.9994 0.9998 1.0000 1.0000 1.0000 12345678 σ0(ω)75.00(5.00%)15.00(1.00%)7.50(0.50%)1.50(0.10%)0.75(0.05%)0.15(0.01%)0.075(0.005%)0.015(0.001%)0.3 9.1 23.2 89.3 99.9 100.0 100.0 100.0 0.0 0.3 1.5 24.9 49.1 99.9 100.0 100.0 0.0 0.0 0.0 0.2 1.7 23.5 47.1 100.0 0.7030 0.9721 0.9927 0.9997 0.9999 1.0000 1.0000 1.0000

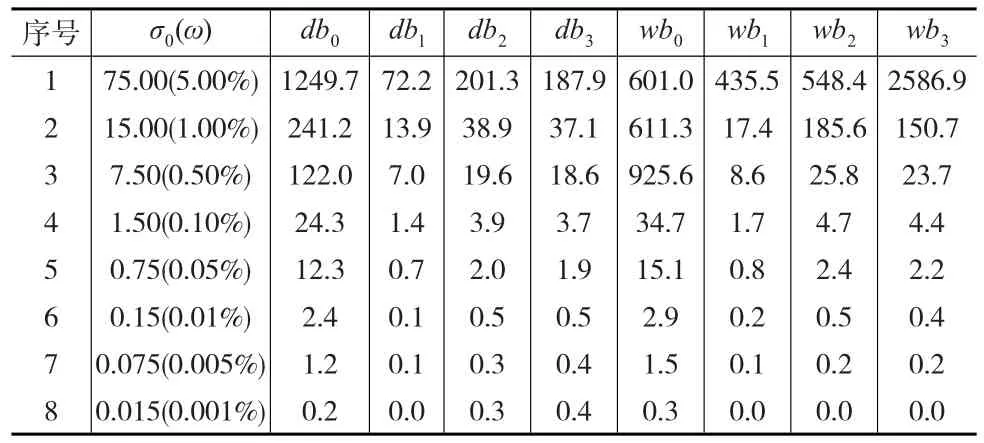
表4回歸系數估值相對真誤差平均值和相對均方誤差平均值的百分比（%）

2.2.1 回歸系數估值的估值漂移

由表3可知，當ω=5%時，回歸系數估值的相對真誤差均小于等于=50%的百分比是0.3%，當ω=1%時，回歸系數估值的相對真誤差均小于等于1=50%的百分比是9.1%，當ω=0.5%時，回歸系數估值的相對真誤差均小于等于1=50%的百分比是23.2%，即回歸系數估值漂移的顯著程度隨著均方誤差系數ω的增大而增大。對于2=10%和2=1%具有相同的結果。

2.2.2 僅用復相關系數和復判定系數說明多元線性回歸的有效性有一定局限性

由表3可知，當ω=1%時，復相關系數和復判定系數總體平均值分別是0.9721和0.9450,回歸系數估值的相對真誤差均小于等于=50%的百分比是9.1%；當ω=0.5%時，復相關系數和復判定系數總體平均值分別是0.9927和0.9855,回歸系數估值的相對真誤差均小于等于=50%的百分比是23.2%。由此可見，即使復相關系數和復判定系數滿足要求，回歸系數的估值也可能產生顯著的估值漂移。

2.2.3 回歸系數估值的有效性和均方誤差系數ω的選取

由表3可知，當ω=0.10%時，回歸系數的相對真誤差均小于等于=50%的百分比是89.3%；即當ω≈0.10%或ω＜0.10%時，回歸系數估值的相對真誤差小于等于=50%，回歸系數估值具有1位有效數字。當ω=0.01%時，回歸系數估值的相對真誤差均小于等于=10%的百分比是100%；即當ω≈0.01%或ω＜0.01%時，回歸系數估值的相對真誤差小于等于=10%，回歸系數估值具有2位有效數字。當ω=0.001%時，回歸系數估值的相對真誤差均小于等于=1.0%的百分比是100%；即當ω≈0.001%或ω＜0.001%時，回歸系數估值的相對真誤差小于等于=1.0%，回歸系數估值具有3位有效數字。

2.2.4 回歸系數估值有效性的判定方法

由表4可知，對于相同的均方誤差系數ω，回歸系數的相對真誤差均值和相對均方誤差均值的各種百分比均接近。比如，在三元仿真實驗中，當ω=0.10%時，回歸系數的相對真誤差均小于等于=50%的百分比是89.3%，其相對均方誤差均小于等于=50%的百分比是88.3%，兩者同時小于等于=50%的百分比是82.3%，數據差距不大，對于相同的均方誤差系數和其相應給定的限值也具有相同的結果。即用回歸系數估值的相對均方誤差和用回歸系數估值的相對真誤差對回歸系數估值的有效性判定基本等價，可用回歸系數估值的相對均方誤差代替回歸系數估值的相對真誤差對回歸系數估值的有效性進行判定。

按照三元線性回歸仿真實驗的方法，本文模擬了二元至五元線性回歸的五組實驗，每組至少整理了五個線性回歸方程來進行仿真實驗，根據每個回歸方程觀測值絕對值均值來模擬觀測值母體均方誤差的大小，從而判斷回歸系數的估值中是否可能會出現估值漂移,并確定判定多元線性回歸系數估值漂移的總體指標。對于不同元的線性回歸方程，則有不同的回歸系數估值漂移總體指標,二元至五元線性回歸系數的估值漂移總體指標見表5。

表5 二元至五元線性回歸系數估值漂移總體指標(%)

3 結論

多元線性回歸中回歸系數的估值可能產生估值漂移，隨著觀測值均方誤差的增大，回歸系數估值漂移的可能性增大。

在二元線性回歸中，當均方誤差系數ω≈1.0%或ω＜1.0%時，回歸系數估值的相對真誤差小于等于=50%（=50%是本文所采用的回歸系數估值漂移的臨界值，根據不同的應用情況可做適當的調整），回歸系數估值具有1位有效數字；當ω≈0.1%或ω＜0.1%時，其相對真誤差小于等于=10%，具有2位有效數字；當ω≈0.01%或ω＜0.01%時，其相對真誤差小于等于=1.0%，具有3位有效數字。為了確保二元線性回歸系數的有效性，至少應當使ω≈0.1%或ω＜0.1%。

在三元至五元線性回歸中，當均方誤差系數ω≈0.10%或ω＜0.10%時，回歸系數估值的相對真誤差小于等于=50%，回歸系數估值具有1位有效數字；當ω≈0.01%或ω＜0.01%時，其相對真誤差小于等于=10%，具有2位有效數字；當ω≈0.001%或ω＜0.001%時，其相對真誤差小于等于=1.0%，具有3位有效數字。為了確保三元至五元線性回歸系數的有效性，至少應當使ω≈0.01%或ω＜0.01%。

用回歸系數估值的相對均方誤差和用回歸系數估值的相對真誤差對回歸系數估值的有效性判定基本等價，可用回歸系數估值的相對均方誤差代替回歸系數估值的相對真誤差對回歸系數估值的有效性進行判定。當回歸系數估值的相對均方誤差大于50%時，就認為回歸系數產生了顯著估值漂移。相對于僅用復相關系數和復判定系數確定多元線性回歸有效性，增加回歸系數估值漂移的確定，對多元線性回歸特別是回歸系數的有效性確定具有更高的可靠性。