基于相關向量機的鋰離子電池剩余壽命預測

李 賽，龐曉瓊，林慧龍，王竹晴

(中北大學 大數據學院，山西 太原 030051)

0 引 言

為了減少因電池故障帶來的人身傷害以及財產損失[1-3]，準確預測電池的剩余使用壽命(remaining useful life，RUL)成為了現有研究的熱點和難點[4]。

目前，將鋰離子電池的RUL預測的方法主要分為基于經驗的統計方法以及基于性能的方法兩大類[5]。后者應用比較廣泛，主要有基于物理模型方法，數據驅動方法以及融合方法[2]。然而在實際應用中，物理模型的電子系統通常復雜，因此其適用性較差。基于數據驅動方法中相關向量機算法優點是它在貝葉斯框架下構建學習機，對核函數選擇沒有約束，其輸出結果能夠反映目標值的不確定性，有很好的泛化能力，算法簡單，容易實現[6]。

本文以容量作為性能參數采用相關向量機(relevance vector machine，RVM)算法對鋰離子電池的剩余使用壽命進行直接預測，得到該電池的剩余壽命的預測值和預測置信區間。

1 相關向量機模型預測原理

相關向量機是Tipping基于貝葉斯框架提出來的[7]。RVM函數形式與支持向量機相同，且均是由核函數將低維非線性向高維線性問題轉化，完成高維特征空間中最優分離超平面的構造，使得平面上較難分的非線性數據分離[8]。

1.1 相關向量回歸描述

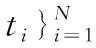
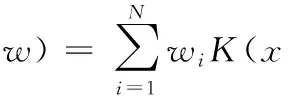
(1)

K(·)是核函數，wi表示RVR的權值N是樣本數。

假定輸出值獨立，數據的噪聲用εi表示，且εi～N(0,σ2)，則帶有噪聲的模型，我們定義為下式

ti=y(xi,w)+εi

(2)

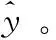
因此，相關向量回歸(relevance vector regression，RVR)表達式為下式

t=φw+ε

(3)

其中，w=(w0,…,wN)T，N+1維列向量,表示RVR的權值；φ是N×M的設計矩陣且φ=(φ0，…,φN)T；φi(xi)=[1,K(xi,x1),…,K(xi,xN)]，i=1,2,…,N；K(·)是核函數。

由于前文中假設ti獨立，得到訓練集的似然函數是

(4)

把超參數引入每一個權值中。相關向量機通過為每一個權值定義了高斯先驗概率分布來約束超參數

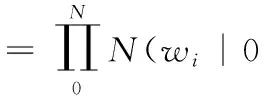
(5)

其中，α={α0,α1,…,αN}是N+1個超參數。

1.2 貝葉斯過程推理

所有未知參數有后驗公式

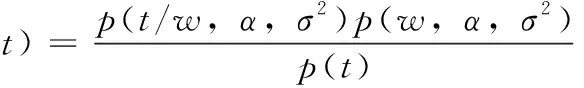
(6)

輸入一個新的觀測值x*，得到對應的預測目標值為

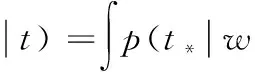
(7)

因為p(w,α,σ2/t)=p(w/α,σ2,t)p(α,σ2/t),所以

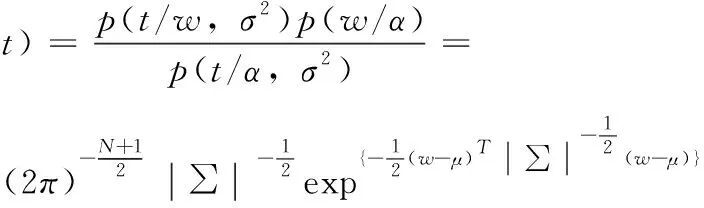
(8)

其中，權重的協方差方差∑=σ2I+ΦA-1ΦT，A=diag(α0,α1,…,αN)，均值μ=∑ΦTBt(B=σ2I)；

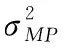
因為p(α,σ2/t)∝p(t/α,σ2)p(α)p(σ2),求出p(t/α,σ2)的最大值即可。

根據

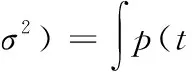
(9)

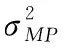
1.3 超參數的更新及RUL預測

(10)

式中:μi是第i個后驗權值的均值，∑ii為后驗方差矩陣的第i個對角線元素。

對式(10)求偏導得

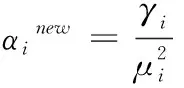
用相同的方法求出噪聲方差

(11)

通過迭代計算式(10)、式(11)，很多超參數會在進行重新估計的過程中趨于無窮大，甚至無限接近于0，所以與之對應的核函數可以刪除，進而達到稀疏化[10]，從而獲得使α和σ2的最大解析表達式。

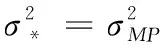
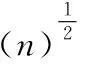
2 仿真實驗設計與分析對比

2.1 仿真實驗設計

實驗目的：為對本文提出的鋰離子電池RUL預測方法進行有效的驗證，將電池的容量數據作為該實驗的樣本數據進行RUL 預測，從而對本文所提方法的預測能力進行評估。

實驗方法：本文的實驗對象選取為NASA提供的公開數據集(B5、B6、B18)，這3種電池的型號和額定參數均相同。設定預測起始時刻，用RVM預測法進行RUL預測。

實驗步驟：本文選擇的容量數據，前60周期用于訓練模型的超參數， 從60周期開始作為預測起始時刻，經仿真實驗，得到對電池容量預測的退化曲線以及預測上限和下限。當電池隨充放電不斷進行，容量達到壽命結束點(end of life，EOL)，即電池容量衰減達到額定容量的70%左右時，實驗終止。實驗時電池的失效閾值設置為1.38 Ah。由于B7電池容量未退化到 1.38Ah，故實驗未采用。最后將預測結束點的循環周期數及其置信區間轉化為RUL值和RUL置信區間，與真實的RUL 進行對比與分析。

2.2 實驗結果分析

2.2.1 容量退化曲線

根據容量的真實值完成4個型號電池的退化曲線，如圖1所示。

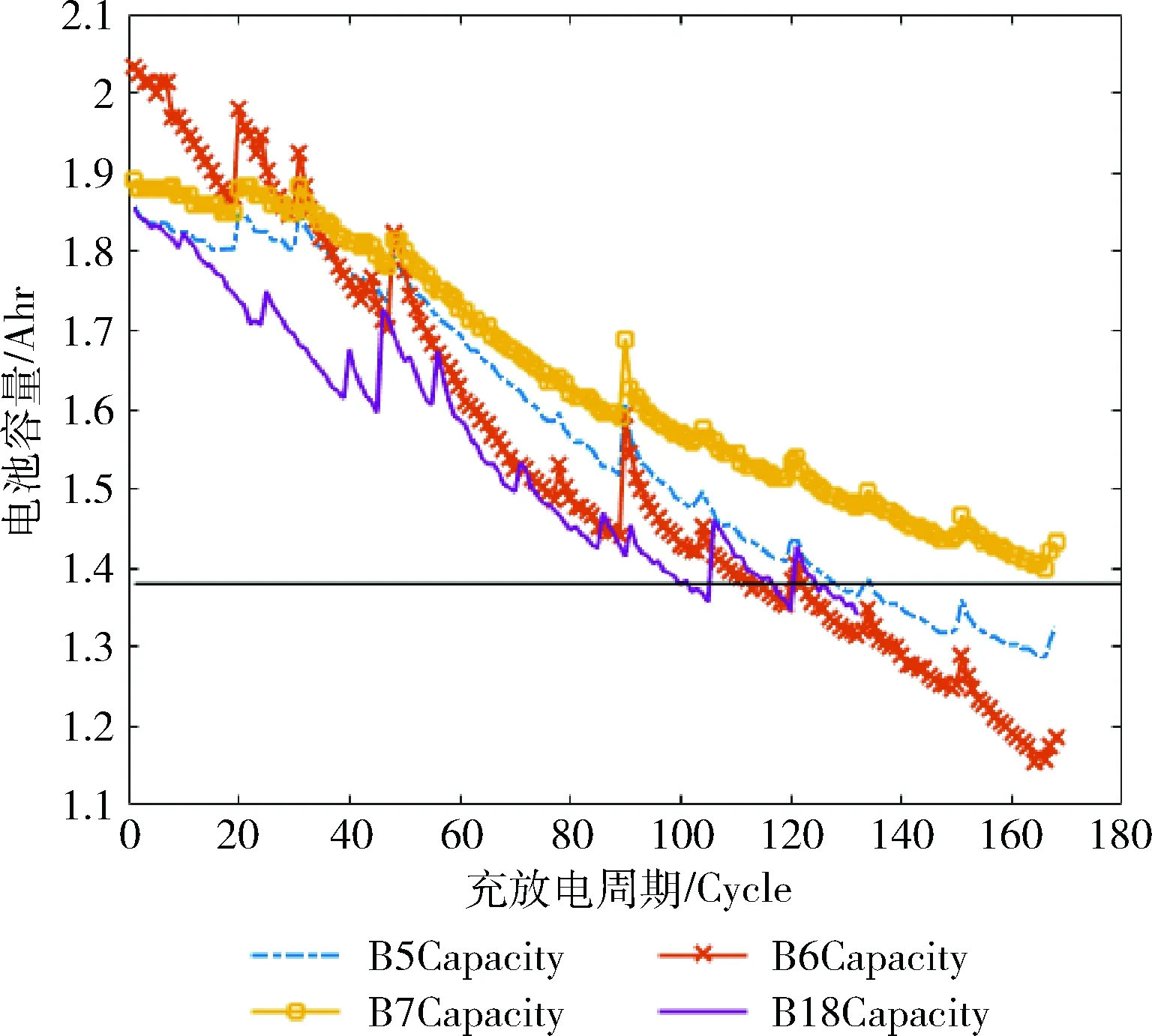
圖1 電池容量退化曲線(B5、B6、B7、B18)

從圖1可知，鋰離子電池的容量隨著充放電次數的增加而減小。其實在電池的使用過程中，導致其性能退化的原因還有很多種，如溫度升高的速度加快、內阻變大等[11]。

2.2.2 RUL預測

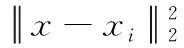
B5、B6、B18電池的預測起始時刻設為60。首先對B5電池進行實驗，得到如圖2所示的結果。

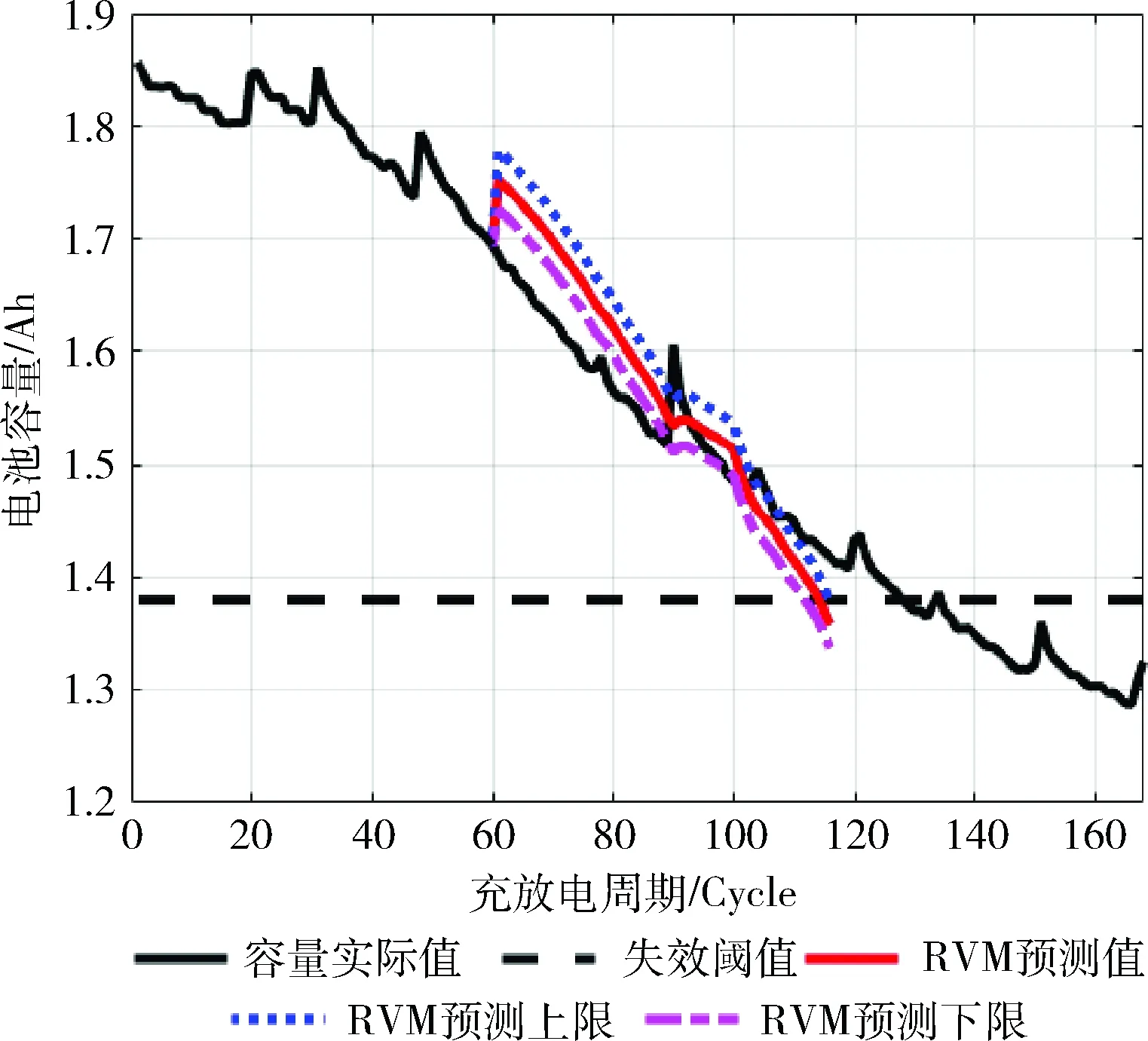
圖2 RVM預測曲線(B5)

在圖2中，黑色虛線代表該電池的失效閾值，黑色實線代表該電池的實驗測量數據，實線曲線表示利用相關向量機的時間序列算法得到的該電池的預測值。點線和點劃線分別表示RVM算法對容量的預測上限和預測下限。

為了進一步的驗證該算法的有效性，我們分別B6和B18電池進行實驗。

對B6電池進行實驗，得到如圖3所示的結果。

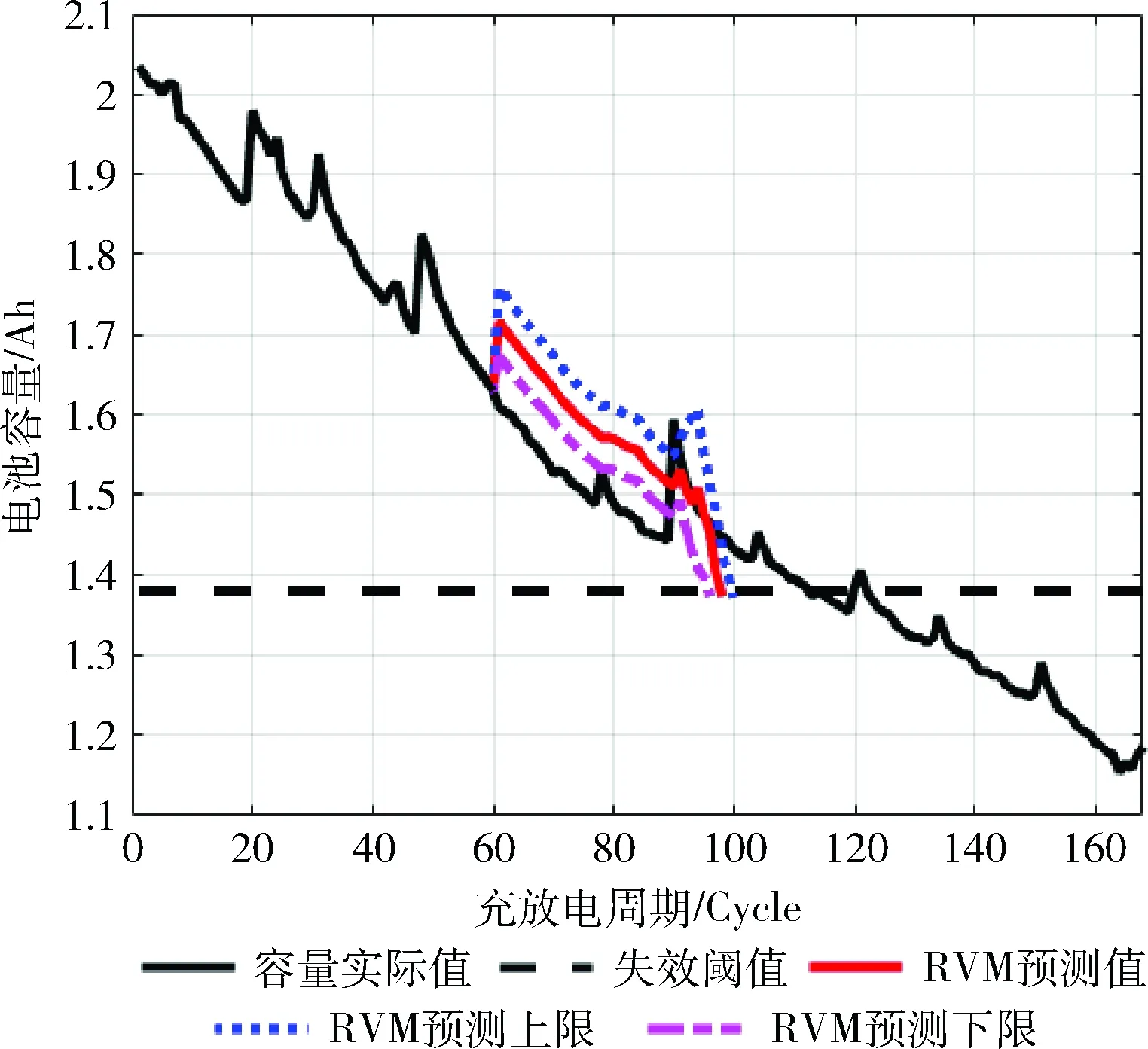
圖3 RVM預測曲線(B6)

對B18電池進行實驗，得到如圖4所示的結果。

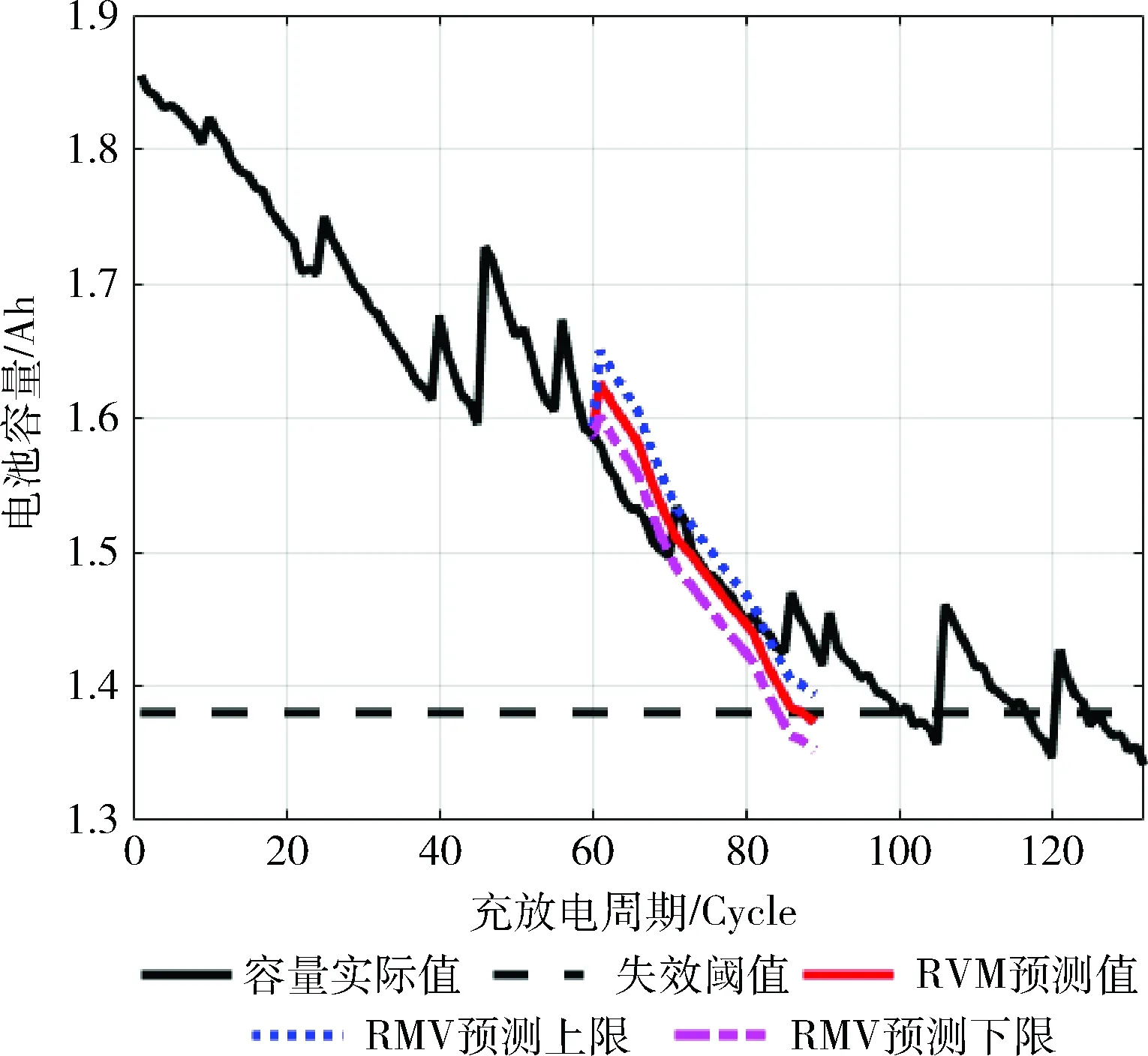
圖4 RVM預測曲線(B18)

從以上3個圖中，我們可以看出，B5、B6、B18電池預測起始點均為第60個周期，壽命結束點的真實值分別是129、113和100周期，預測結果分別是114、97和87周期。B5電池壽命的預測下限和上限分別是116和112周期；B6電池壽命的預測下限和上限分別是99和95周期；B18電池預測上限和下限分別是89和84周期。具體結果見表 1。

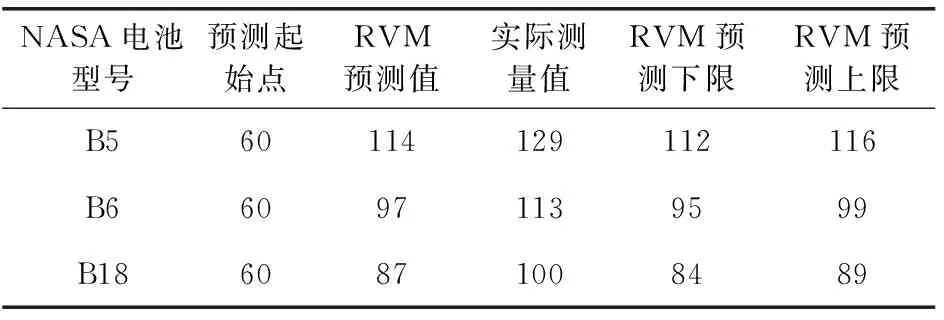
表1 RVM預測值及其預測上限和下限

2.3 實驗分析

本文中RVM超參數的設置對容量的預測結果有直接的影響，比如樣本數據的多少和高斯核函數中核寬度的設置決定了模型的稀疏性和精確性[12],本文分別對B5、B6、B18電池進行實驗，它們的起始預測周期均為60周期，電池的真實使用壽命終點分別為129、113和100周期,并仿真出容量預測值，見表2。

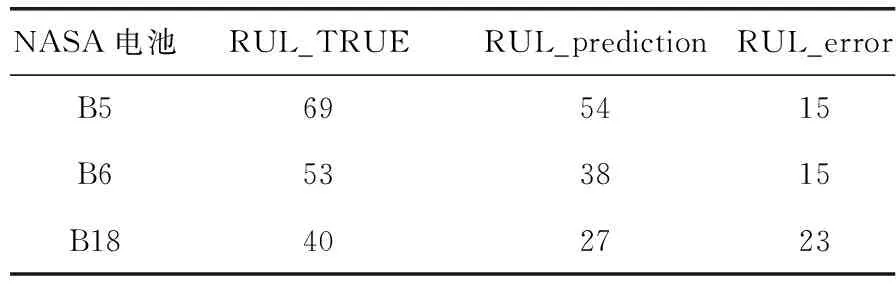
表2 采用RVM的RUL預測結果

在表2中，RUL_prediction表示利用RVM預測所得的鋰離子電池的剩余循環使用壽命，RUL_error表示RUL的絕對誤差值，定義為：

RUL_error=RUL_prediction-RUL_true其中，RUL_true表示設置預測起始點后電池的真實剩余循環使用壽命。

由表1得出，B5、B6、B18的RUL_true分別是129-60=69周期、113-60=53周期和100-60=40周期。采用相關向量機算法預測的剩余使用壽命分別是RUL_prediction=114-60=54個周期、RUL_prediction=97-60=37個周期和RUL_prediction=87-60=27個周期。預測的循環使用壽命誤差分RUL_error=69-54=15、RUL_error=53-37=16和RUL_error=40-27=13。

2.4 相關向量機算法與擴展卡爾曼濾波算法對比實驗分析

為了進一步說明相關向量機算法的有效性，現在將該算法和擴展卡爾曼濾波(extended kalman filter，EKF)的RUL預測周期和預測誤差進行對比，預測周期見表3。

從表3中可以得到，B5、B6、B18號電池在相同的預測起點第60個周期時，相關向量機方法對鋰離子電池的RUL預測結果分別為54、38和27個周期。擴展卡爾曼濾波方法得到的B5電池預測結果分別為49個周期，B6電池僅為24個周期，B18電池為14個周期。

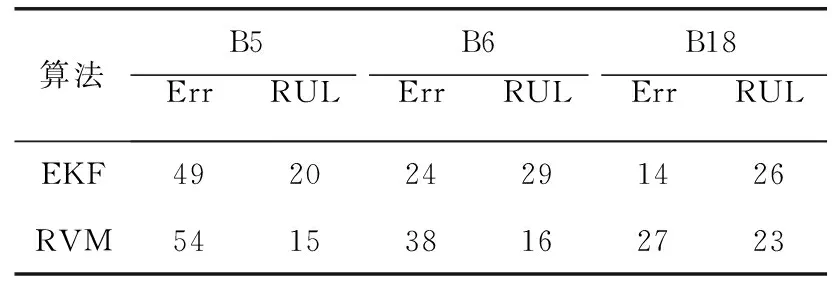
表3 兩種方法的RUL預測結果及誤差對比

為了較準確對兩種算法分析對比，引入絕對誤差均值(mean absolute error，MAE)與均方根誤差(root mean square error，RMSE)。

式中:n是預測數據的長度，x_real(i)是第i次預測時的真實容量值，x_m(i)是第i次預測的容量值，該電池平均絕對誤差和均方根誤差見表4。

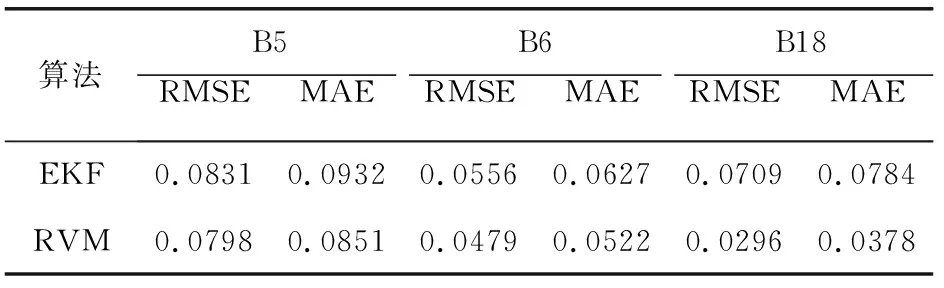
表4 兩種方法的RUL預測誤差

從表4中可以得到RVM算法的誤差均小于EKF的誤差，即RVM算法的預測精度高于EKF的預測精度。

3 結束語

鋰離子電池已經被應用在生活、工業等領域，其工作性能狀態的在線監測和預測性維護已成為研究熱點，并已在電子系統故障預測和健康管理技術領域形成新的研究熱點。

本文借鑒了時間序列多步預測的遞推計算的思想，實現了鋰離子電池RUL預測，并給出了電池壽命的置信區間，充分考慮了遞推過程中預測不確定性的傳遞問題。與擴展卡爾曼濾波算法相比,本文的獨特之處為該算法輸出的鋰離子電池的剩余壽命分布能夠更加有效地反映各種不確定性和隨機因素,比較符合實際情況。