隨機沖擊影響的多部件退化設(shè)備壽命預(yù)測方法

白 燦， 胡昌華， 張建勛， 裴 洪， 張 鵬， 張 優(yōu)

(火箭軍工程大學(xué)，陜西 西安 710025)

0 引 言

現(xiàn)代工程設(shè)備，如航天工業(yè)中的在軌飛行器、電力工業(yè)中的各類電機等都是具有復(fù)雜系統(tǒng)的設(shè)備。當(dāng)其中某些部件發(fā)生異常時，若未及時發(fā)現(xiàn)或維修不足，將有可能導(dǎo)致整個設(shè)備的失效，從而產(chǎn)生不可估量的后果[1]。從設(shè)備喪失規(guī)定功能形式來看，失效可分為退化失效和突發(fā)失效。退化失效即設(shè)備在正常工作過程中經(jīng)歷的緩慢老化直至達(dá)不到工作指標(biāo)要求；突發(fā)失效指設(shè)備在正常工作期間內(nèi)由于偶然的外界因素如沖擊、擊穿、短路等造成的意外失效。因此根據(jù)設(shè)備的失效機理建立合理的退化模型對其可靠性進行有效評估并預(yù)測壽命具有重要的現(xiàn)實意義。

當(dāng)前設(shè)備可靠性評估及壽命預(yù)測方法已得到廣泛研究。文獻[2]系統(tǒng)地從數(shù)據(jù)采集、健康因子、狀態(tài)階段以及壽命預(yù)測4個方面對設(shè)備的預(yù)測研究方法進行了回顧與總結(jié)。文獻[3]和[4]以維納過程為基礎(chǔ)建立連續(xù)退化模型，研究了慣性平臺系統(tǒng)中的陀螺儀分別為線性退化和非線性退化時的壽命預(yù)測問題；文獻[5]基于布朗運動建立了具有自適應(yīng)漂移系數(shù)的壽命預(yù)測模型，利用連續(xù)攪拌釜反應(yīng)器產(chǎn)生的實驗數(shù)據(jù)驗證模型有效性及預(yù)測精度。特別地，隨機系數(shù)回歸模型[6]、馬爾科夫鏈[7]、伽瑪過程[8]、逆高斯過程[9]等都廣泛應(yīng)用于退化建模和壽命預(yù)測領(lǐng)域。上述研究大都在設(shè)備正常退化的基礎(chǔ)之上開展的，實際工程中設(shè)備由于轉(zhuǎn)運、測試、磨損、沖擊等原因，會加速其性能退化。在可靠性領(lǐng)域中，有大量考慮沖擊影響的退化設(shè)備研究。文獻[10]采用多狀態(tài)模型刻畫沖擊退化過程并給出了系統(tǒng)可靠性方程；文獻[11]基于Brown-proschan模型，考慮了沖擊效應(yīng)、沖擊到達(dá)以及故障率3者之間關(guān)系并給出其可靠性方程。文獻[12]將沖擊損傷刻畫為固定常數(shù)，研究了線性退化設(shè)備設(shè)備剩余壽命自適應(yīng)預(yù)測問題，并將理論應(yīng)用于銑刀切削金屬材料的運行退化過程。

上述研究工作大都基于單部件設(shè)備的退化過程進行研究，而現(xiàn)代工業(yè)設(shè)備大多由多部件系統(tǒng)組成。文獻[13]針對多部件系統(tǒng)建立了多依賴競爭失效過程模型，考慮了軟失效對系統(tǒng)連續(xù)退化的影響以及硬失效對系統(tǒng)退化突發(fā)的影響；文獻[14]分別考慮了沖擊對系統(tǒng)退化量和退化速率的影響，為依賴競爭失效的系統(tǒng)提供多目標(biāo)優(yōu)化的不完善預(yù)防性維護策略；文獻[15]以一個組件間串聯(lián)的系統(tǒng)為研究對象建立可靠性模型，分析了沖擊引發(fā)的軟、硬失效相互競爭的可靠性評估；文獻[16]針對沖擊影響的系統(tǒng)建立退化與突發(fā)競爭失效過程的可靠性模型，評估系統(tǒng)可靠性并提出了基于狀態(tài)的維修策略；文獻[17]以沖擊載荷影響下的多競爭失效系統(tǒng)為研究對象，采用Copula函數(shù)描述退化和沖擊影響之間的相關(guān)性，對系統(tǒng)可靠性進行評估。可以看出，盡管針對多部件設(shè)備沖擊與退化過程已有相當(dāng)?shù)难芯抗ぷ鳎跊_擊對退化影響之間的相關(guān)性和系統(tǒng)壽命預(yù)測領(lǐng)域仍缺乏較好的研究。針對這些問題，區(qū)別于上述方法，本文基于競爭失效過程提出一種退化沖擊模型，并考慮了隨機沖擊對各部件硬失效影響之間的相關(guān)性進而分析設(shè)備的可靠性及壽命分布。

1 問題描述與建模

1.1 問題描述

針對存在隨機沖擊影響下的多部件退化設(shè)備壽命預(yù)測問題，可由圖1進行描述。圖1（a）反映的是部件i正常退化和沖擊導(dǎo)致的累積損傷情況，橫坐標(biāo)為時間，縱坐標(biāo)反映了設(shè)備性能隨時間t變化的狀態(tài)退化量{M(t),t≥0}。ωMi為部件i的軟失效閾值，T1，T2，T3···為沖擊到達(dá)時刻。若部件的退化水平Mi(t)達(dá)到ωMi，則導(dǎo)致軟失效發(fā)生。圖1（b）表示的是部件i由于設(shè)備受到?jīng)_擊造成的突發(fā)影響情況，ωVi為部件i的硬失效閾值，當(dāng)設(shè)備受到的沖擊大小傳輸?shù)讲考超過ωVi時，設(shè)備發(fā)生硬失效，且兩種失效模式相互獨立。

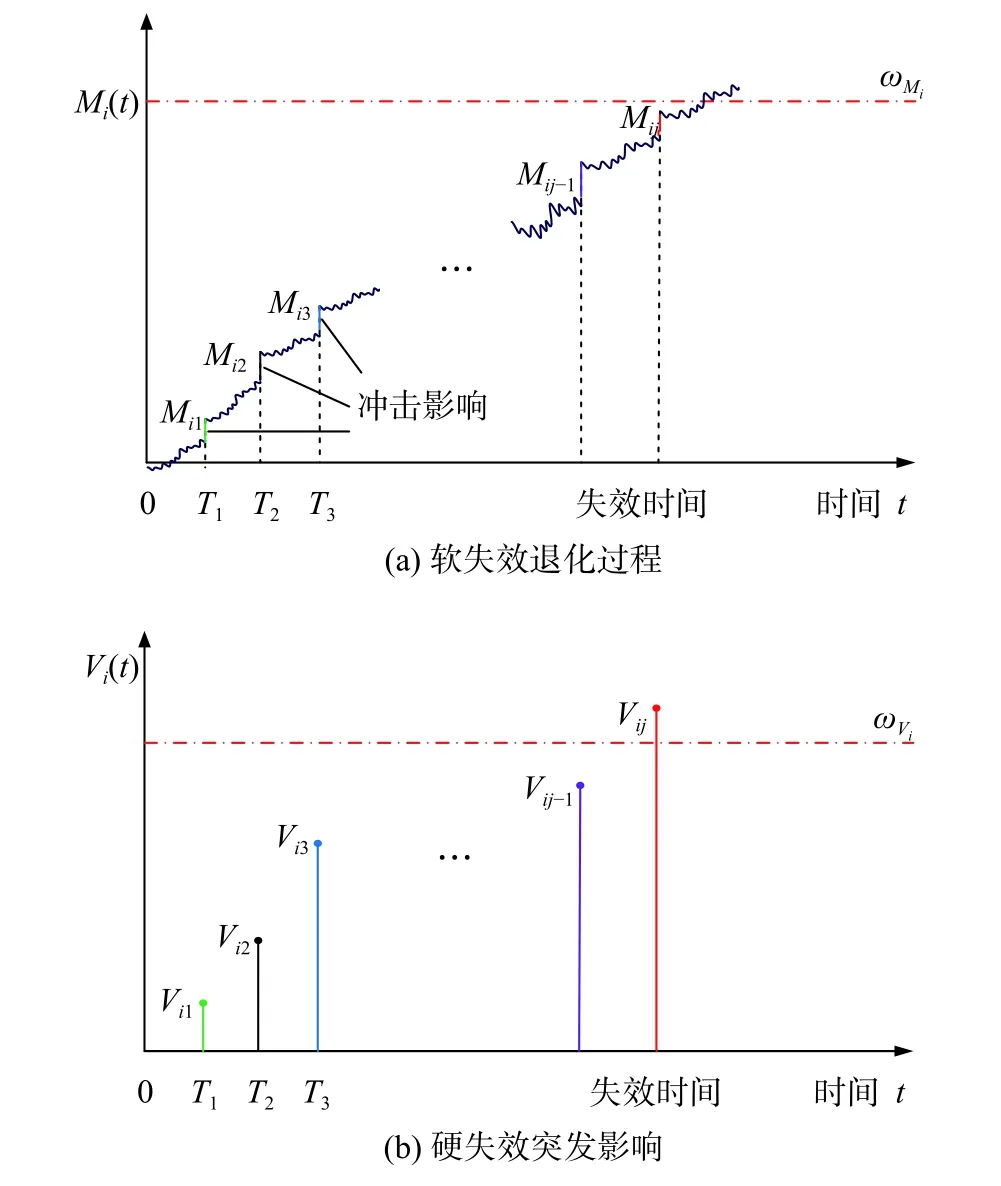
圖1 考慮隨機沖擊影響下的部件i退化軌跡

1.2 退化建模

用隨機過程{Mi(t),t≥0}刻畫設(shè)備中部件i的正常退化和累積沖擊過程。根據(jù)上述分析可建立模型如下：

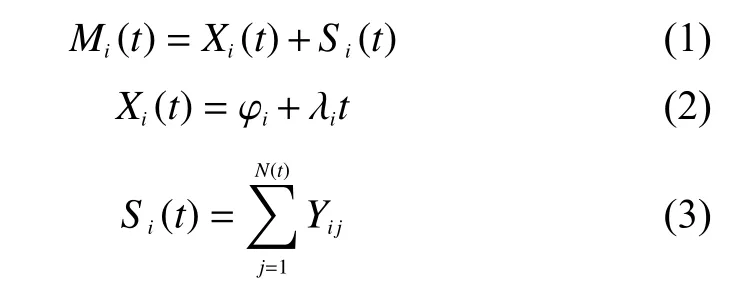
當(dāng)設(shè)備受到外界沖擊影響時傳輸?shù)讲考的突發(fā)性沖擊分量大小為

其中Mi(t)為第i個部件在t時刻經(jīng)歷的自然退化和沖擊導(dǎo)致的累積退化量之和。Xi(t)是第i個部件正常退化量，為考慮模型適用性，一般采用部件為線性退化軌跡模型[18-20]。其中，φi為 初始退化量，λi為部件的線性退化速率，λi可以是固定常數(shù)也可以是隨機變量，當(dāng)λi為隨機變量時更貼合于實際退化的不確定性，本文假定λi是服從高斯分布的隨機變量。Yij是設(shè)備經(jīng)歷的第j次沖擊對第i個部件造成的軟失效損傷影響，Si(t)是設(shè)備經(jīng)歷的所有沖擊對第i個部件造成的基于正常退化之外的累積損傷，與對其他部件影響類似。{N(t),t≥0}是發(fā)生率為γ(t)的泊松過程，表示在一定時間間隔內(nèi)發(fā)生沖擊的次數(shù)，且N(0)=0。若γ(t)取為常數(shù)，則N(t)是發(fā)生率固定的泊松過程。Vij是設(shè)備經(jīng)歷的第j次沖擊對第i個部件造成的硬失效突發(fā)影響，為第j次沖擊對第i部件造成的與沖擊大小無關(guān)的退化影響，αi為硬失效沖擊傳輸參數(shù)，Zj為設(shè)備經(jīng)歷的第j次沖擊大小。

2 可靠性及壽命分布

2.1 兩種失效模式介紹

硬失效即為突發(fā)性實效，如圖1（b）所示，當(dāng)部件i經(jīng)歷沖擊j后承受的沖擊量大小Vij超過硬失效閾值ωVi導(dǎo)致硬失效發(fā)生。部件i受到第j次沖擊不發(fā)生硬失效的概率可由文獻[13]得到

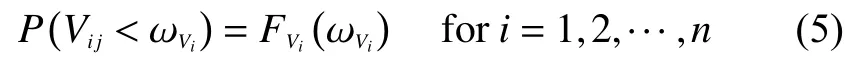
公式（5）是不帶有任何參數(shù)設(shè)定的通用公式，

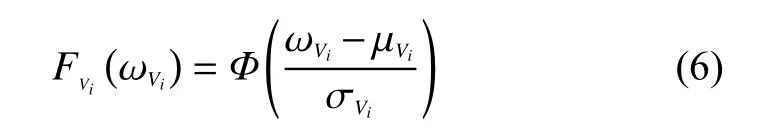
其中，Φ(·)為標(biāo)準(zhǔn)正態(tài)隨機變量的累積分布函數(shù)（cumulative distribution function，CDF）。值得注意的是，一個普通正態(tài)分布隨機變量可能有負(fù)值，然而實際中，由沖擊造成的退化增量Vij一定是非負(fù)的，因此，選取合適的隨機變量均值和方差使得Vij為負(fù)數(shù)的概率忽略不計是至關(guān)重要的。

軟失效即為退化型失效，本文指部件自然退化和隨機沖擊導(dǎo)致的累積退化量超過設(shè)備自然退化的閾值后發(fā)生的失效。如圖1（a）所示，對于部件i，在正常退化和沖擊造成的累積退化影響之和Mi(t)超過軟失效閾值ωMi時，軟失效發(fā)生。t時刻總退化量Mi(t)低于一個特定值mi的概率可由文獻[13]得到

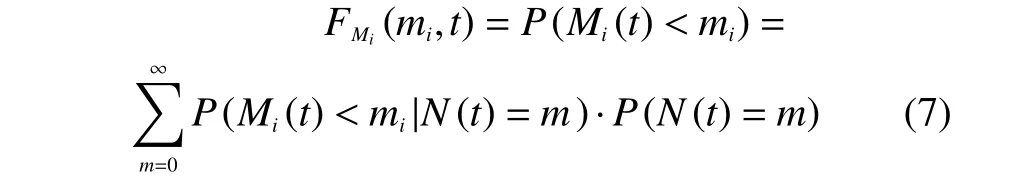
假定沖擊的到達(dá)服從發(fā)生率為固定值γ的泊松過程，則在t時刻，發(fā)生數(shù)量為m個沖擊的概率為exp(?γt)(γt)m/m！。定義在t時刻的CDF，為m個 獨立同分布變量Yij的聯(lián)合概率密度函數(shù)（probability density function，PDF），則根據(jù)參考文獻[13]可得到

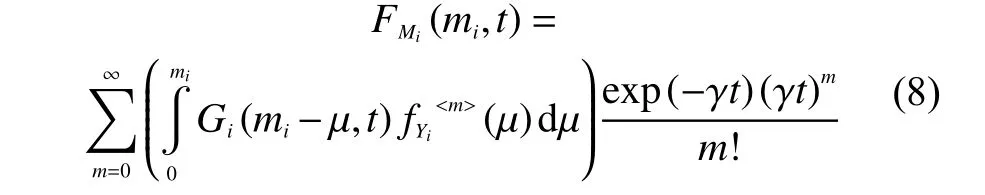
給定沖擊對部件i造成的軟失效退化影響Yij服從正態(tài)分布退化速率服從正態(tài)分布則基于公式（8），可得到進一步的顯示結(jié)果

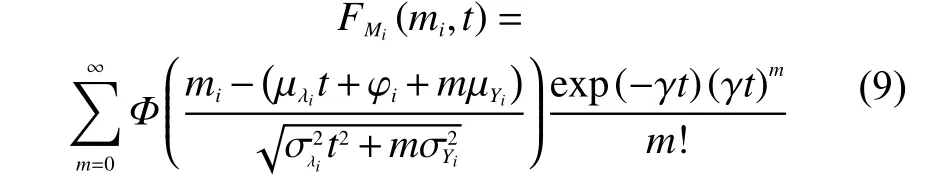
公式（8）可以適用于不同情況時的參數(shù)設(shè)定組合，公式（9）僅提供了一個便于得到顯示結(jié)果的特例，當(dāng)模型中參數(shù)服從其他分布時可以以此類推。實際上，λi和Yij同樣是非負(fù)的，根據(jù)選擇合適的正態(tài)分布均值和方差可以使這兩個變量為負(fù)的概率忽略不計。

2.2 可靠性R(t)與壽命分布PDF

根據(jù)參考文獻[13]，當(dāng)沖擊造成的硬失效影響Vij與軟失效損傷Yij之間相互獨立時，多部件串聯(lián)系統(tǒng)的可靠性函數(shù)為

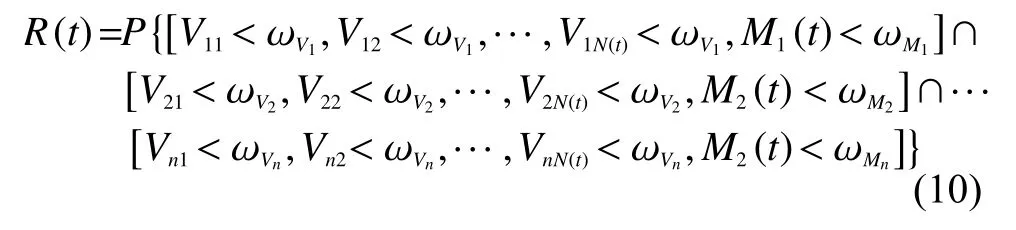
實際上，由系統(tǒng)沖擊對各部件造成的退化影響一般不是相互獨立的。本文模型中，為將沖擊效應(yīng)更好融入到退化過程中，假定設(shè)備經(jīng)歷的沖擊對各部件的硬失效影響V1m,V2m,···,Vnm與設(shè)備經(jīng)歷的第m次沖擊大小為線性相關(guān)，不失一般性，假定軟失效過程中沖擊損(傷Yij服從獨立)同分布的正態(tài)隨機變量。變量V=V1j,V2j,···,Vnj的聯(lián)合累積分布函數(shù)FV(v)為

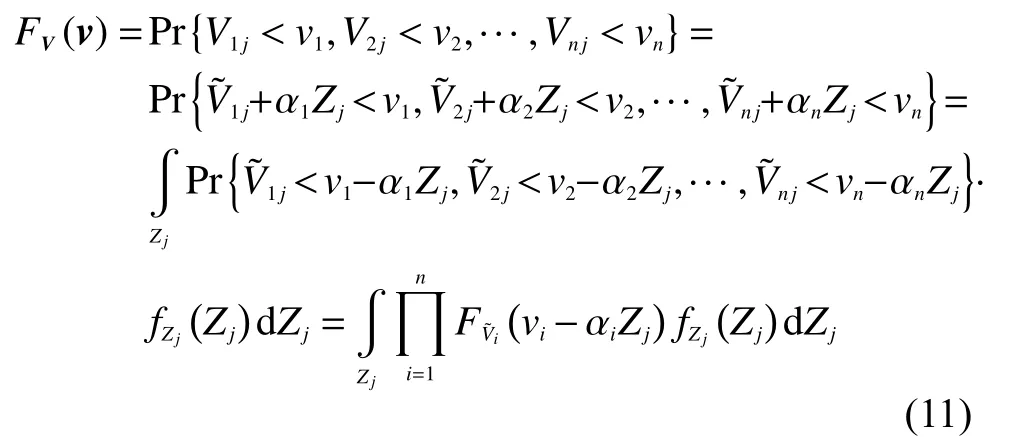
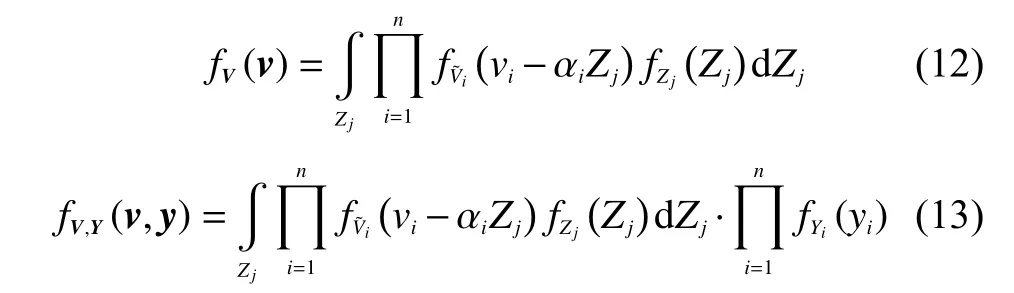
對于一個部件間串聯(lián)的設(shè)備，考慮在t時刻發(fā)生沖擊的數(shù)量，同時考慮由沖擊對各部件帶來的硬失效影響相關(guān)性時，設(shè)備可靠度函數(shù)為

在經(jīng)歷一定數(shù)量的沖擊后，由于部件間發(fā)生軟失效和硬失效過程是相互獨立的，則公式（14）可進一步簡化為

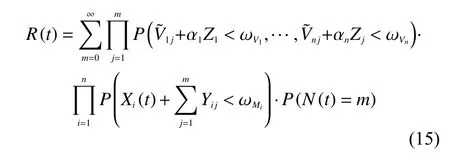
由于沖擊到達(dá)服從發(fā)生率為γ的泊松分布，在設(shè)備經(jīng)歷的第j個沖擊大小已知的條件下對所有zj的值進行積分可得

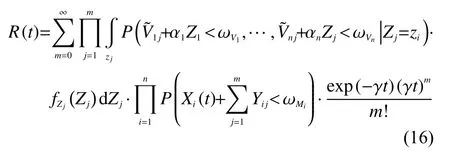
進而轉(zhuǎn)化為

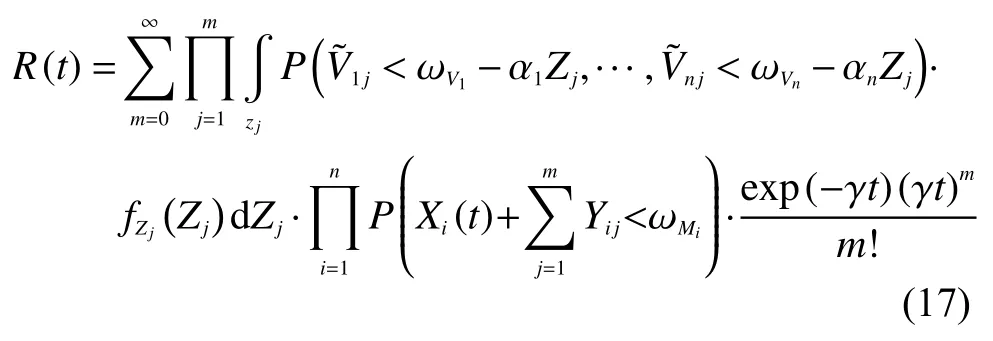
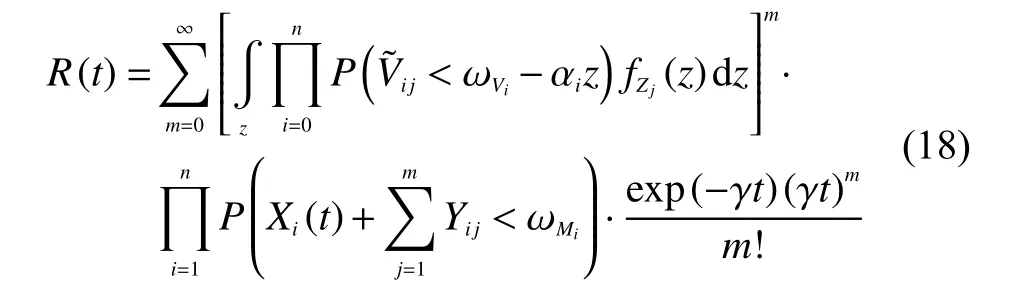
基于本文帶有隨機沖擊效應(yīng)的退化模型，利用卷積積分特性由公式（18）可得到

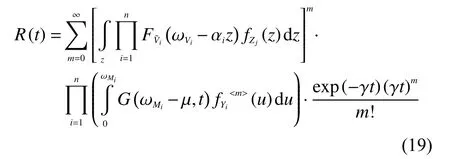
公式（19）是一個一般通用性的可靠度函數(shù)表達(dá)式，可以適用于本模型中參數(shù)的不同分布情況。給定沖擊數(shù)量m一個上限值，并利用數(shù)值積分，即可求解。作為實例驗證，當(dāng)參數(shù)Vij,Yij,Zj均服從正態(tài)分布時，公式（19）可以進一步表示為

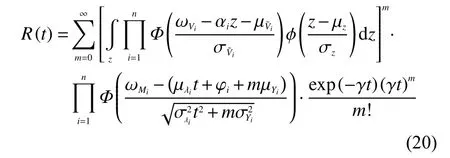
與可靠度函數(shù)相比，設(shè)備的壽命分布概率密度函數(shù)能夠更多地掌握有關(guān)設(shè)備的壽命信息，知道壽命分布PDF可以清楚了解到工作設(shè)備的大概使用壽命，為后續(xù)設(shè)備的定期檢修、維護更換、健康管理等決策提供技術(shù)支持。由參考文獻[17]得到壽命分布累計分布函數(shù)F(t)和概率密度函數(shù)f(t)分別為

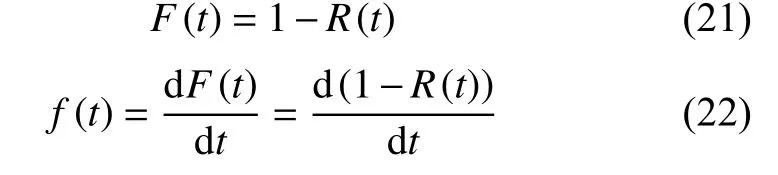
由于公式（20）的復(fù)雜性導(dǎo)致求出f(t)的顯示結(jié)果表達(dá)式相當(dāng)困難，因此借用數(shù)值計算的方法并利用Matlab軟件可對其壽命分布f(t)進行求解和分析。

3 數(shù)值仿真

在仿真研究方面，以一個三部件串聯(lián)系統(tǒng)為例，通過分別改變刻畫系統(tǒng)沖擊參數(shù)μz和σz以及γ三者其中之一和固定其他兩個參數(shù)的大小來模擬隨機沖擊對三部件系統(tǒng)可靠性函數(shù)及壽命預(yù)測精度的影響。作為前提，退化沖擊系統(tǒng)各參數(shù)需要事先給定，系統(tǒng)仿真參數(shù)設(shè)定如表1，沖擊參數(shù)改變情況如表2。分別實現(xiàn)3組模擬仿真，一方面用于驗證先前方法得到的系統(tǒng)可靠性及壽命分布結(jié)果有效性；另一方面，通過參數(shù)的改變說明隨機沖擊對壽命預(yù)測精度的影響。具體仿真結(jié)果，如圖2～圖7所示。

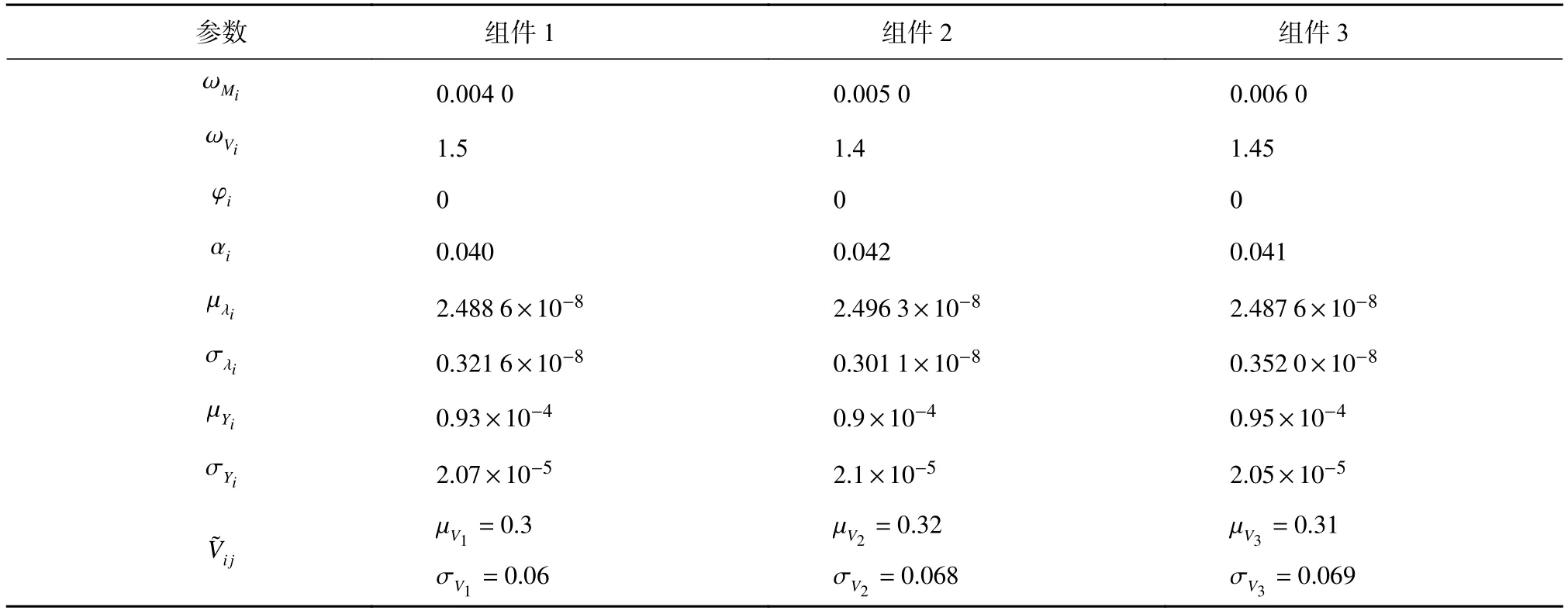
表1 仿真參數(shù)設(shè)定

表2 系統(tǒng)沖擊參數(shù)設(shè)定

上述仿真結(jié)果表明改變多部件設(shè)備經(jīng)歷的隨機沖擊參數(shù)均值μz、方差σz以及發(fā)生率γ的大小都會對多部件設(shè)備的可靠度函數(shù)R(t)以及壽命分布PDF造成影響。首先，根據(jù)圖2、圖4、圖6可以看出增加μz、γ都會不同程度地使可靠度函數(shù)下移，導(dǎo)致設(shè)備提前失效，增加σz會使可靠度函數(shù)上移，設(shè)備失效提前，失效風(fēng)險降低，這是符合客觀實際的。其次，圖3、圖5、圖7表明增加μz會導(dǎo)致壽命分布的方差減小而均值保持不變；增加σz會導(dǎo)致壽命分布方差增大而均值保持不變；而增加γ既會導(dǎo)致壽命分布的方差減小同時也會導(dǎo)致壽命分布的均值減小。

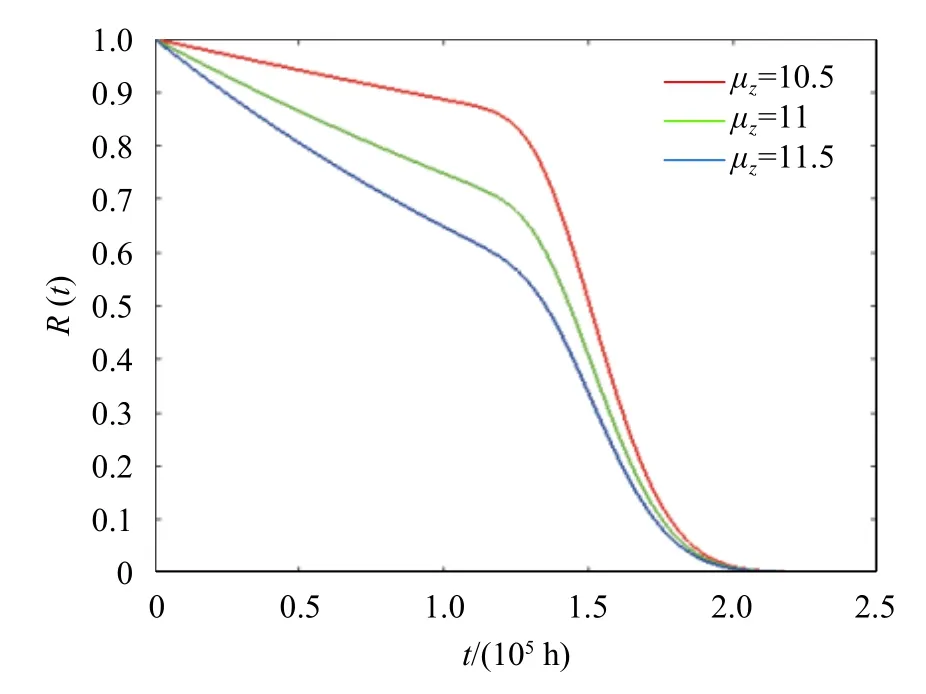
圖2 不同μz值時設(shè)備可靠度函數(shù)曲線

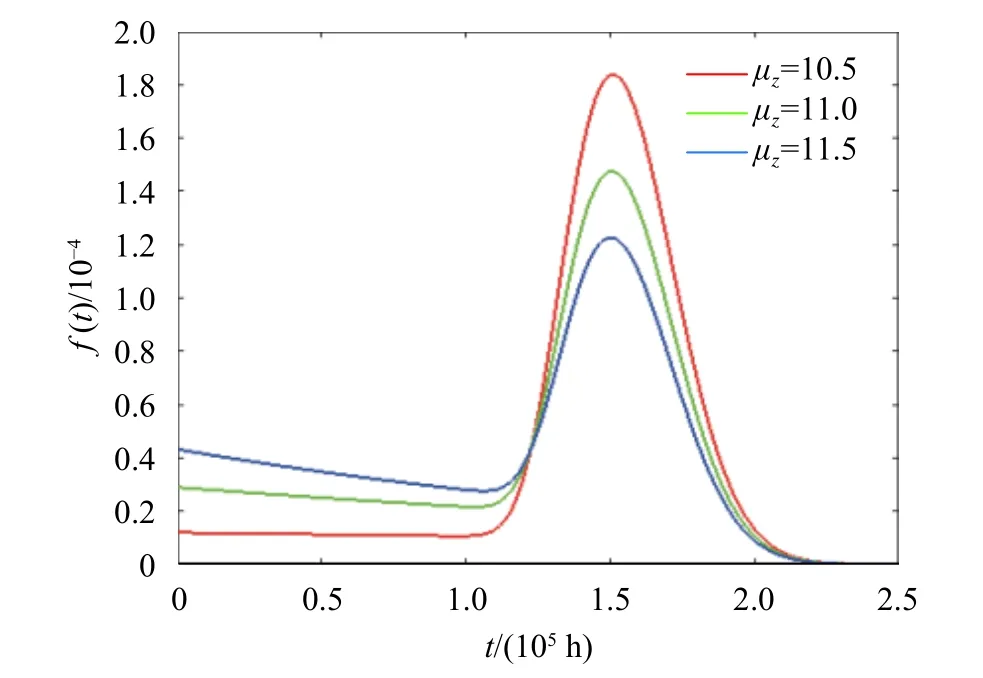
圖3 不同μz值時設(shè)備壽命分布PDF

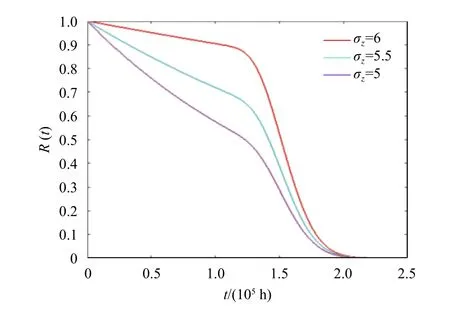
圖4 不同σz值時設(shè)備可靠度函數(shù)曲線

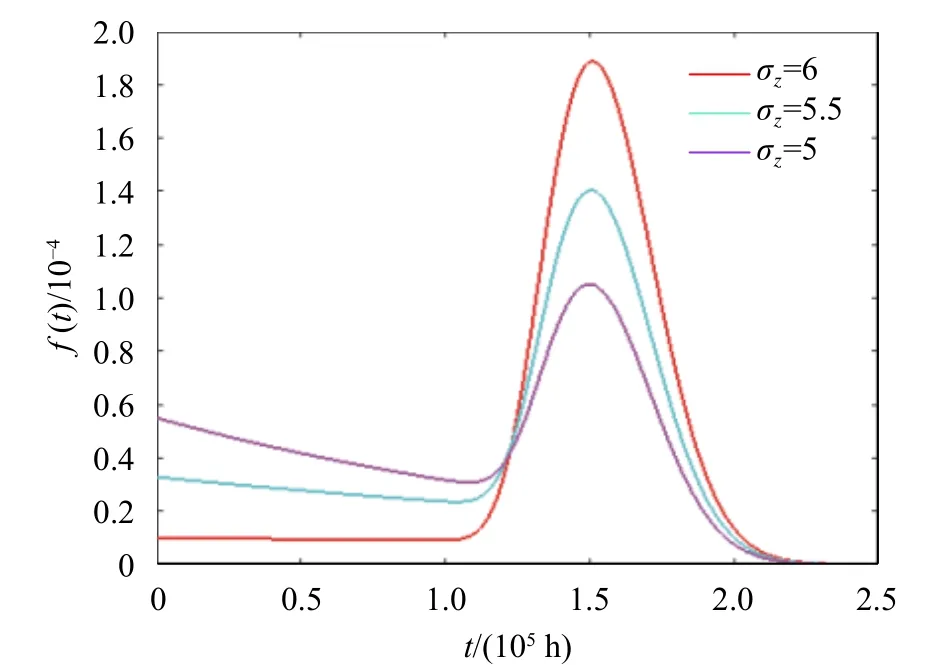
圖5 不同σz值時設(shè)備壽命分布PDF

4 實例驗證

將本文所提方法應(yīng)用于分析微機電系統(tǒng)（micro electromechanical system，MEMS）退化現(xiàn)象。采用美國圣地亞國家實驗室微機電系統(tǒng)可靠性試驗時記錄的參數(shù)值[21]。MEMS大多為一個獨立的智能系統(tǒng)，其主要由傳感器、執(zhí)行器和微能源3大部件組成，在國民經(jīng)濟和軍事系統(tǒng)方面有著廣泛的應(yīng)用前景。本實驗采用的微電機系統(tǒng)由4個組件串聯(lián)組成，組件1和組件2退化特性相同，組件3和組件4退化特性相同。模型中參數(shù)的取值見表3。同時為了體現(xiàn)本文所提模型的優(yōu)越性，將隨機沖擊導(dǎo)致的硬失效影響相互獨立的模型與本文模型作比較。具體結(jié)果如圖8、圖9所示。

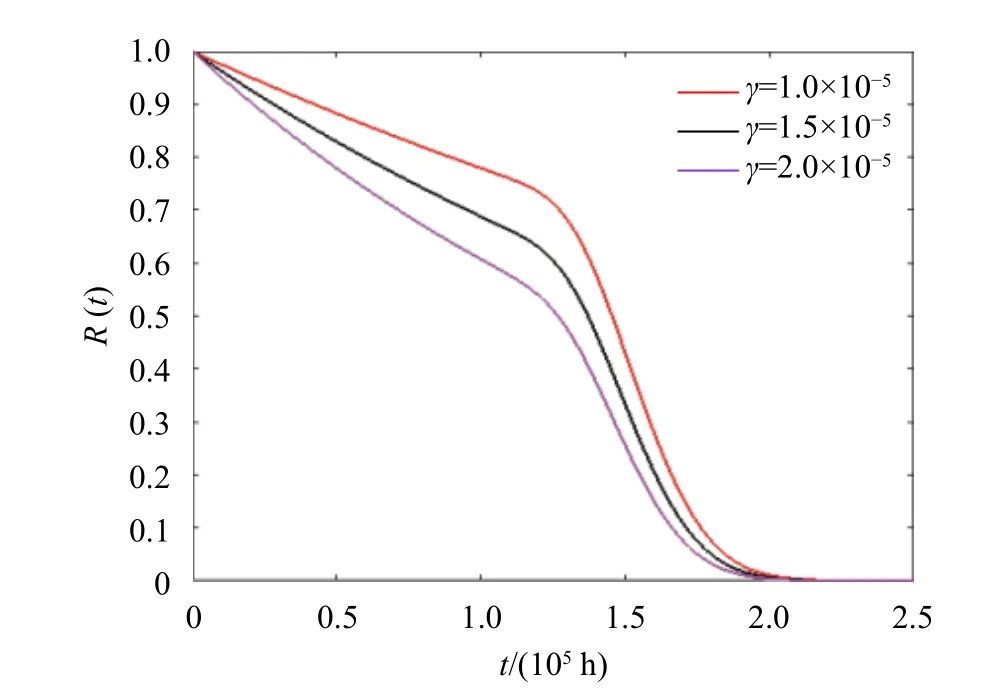
圖6 不同γ值時設(shè)備可靠度函數(shù)曲線

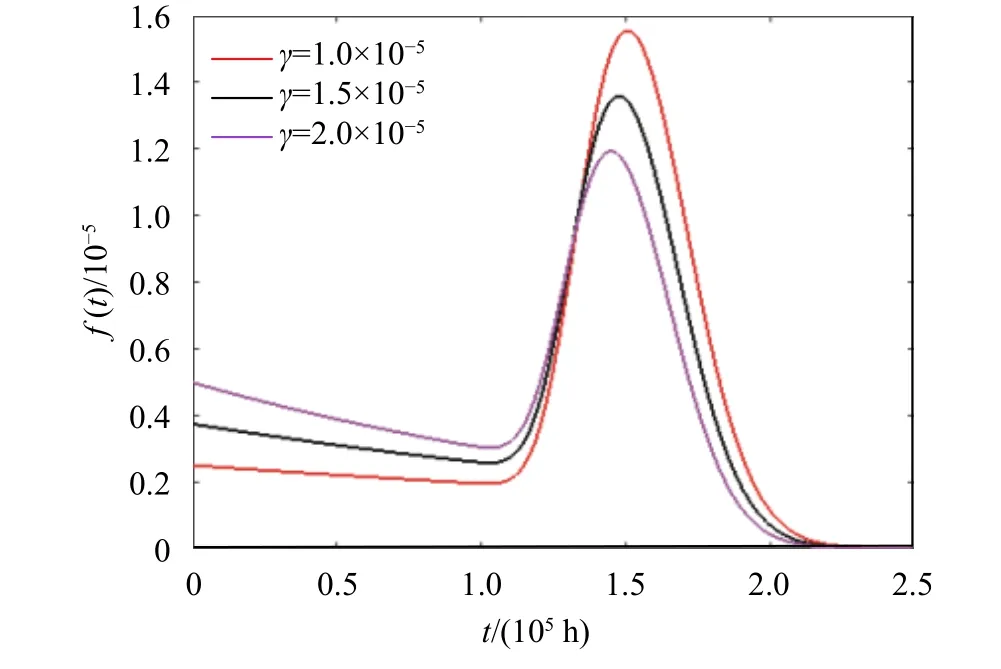
圖7 不同γ值時設(shè)備壽命分布PDF

從實例驗證的結(jié)果對比中可以看出隨機沖擊導(dǎo)致硬失效影響的相關(guān)性對多部件設(shè)備的可靠性以及壽命分布的影響。圖8表明考慮沖擊對硬失效之間相關(guān)性的設(shè)備可靠度函數(shù)R(t)曲線下降速率更快，若不考慮其相關(guān)性可能導(dǎo)致對其可靠性的過高評估，在系統(tǒng)投入使用后期(t>130000h)后兩曲線重合，這是由于在設(shè)備壽命后期硬失效影響間的相關(guān)性體現(xiàn)的不再明顯。圖9結(jié)果表明，在設(shè)備投入使用的中后期之前(t＜100000h)，硬失效影響之間相關(guān)性對壽命分布的影響大于不考慮其相關(guān)性，在設(shè)備投入使用的中后期之后(t>100000h)，考慮沖擊對硬失效影響之間的相關(guān)性對壽命分布影響體現(xiàn)得也不再明顯。因此，在設(shè)備壽命周期的中前期，考慮該相關(guān)性與否會較大地影響工程實際中對多部件退化設(shè)備的可靠性評估與壽命預(yù)測預(yù)測的精度。

表3 微電機系統(tǒng)參數(shù)值

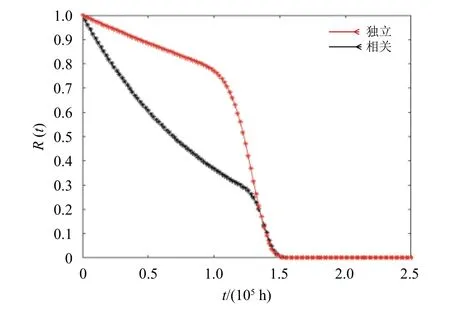
圖8 微機電系統(tǒng)可靠度函數(shù)

5 結(jié)束語

本文研究了考慮隨機沖擊影響的多部件退化設(shè)備可靠性及壽命預(yù)測方法，基于競爭失效過程建立了多部件設(shè)備退化沖擊模型，通過復(fù)合泊松過程描述沖擊對設(shè)備各部件退化的累積影響。基于軟失效和硬失效相互競爭并同時考慮沖擊對硬失效影響之間的相關(guān)性求出設(shè)備的可靠度函數(shù)表達(dá)式，進而得到其壽命分布。數(shù)值仿真通過分別改變不同沖擊參數(shù)的大小說明沖擊對退化設(shè)備的可靠度函數(shù)及壽命分布均值和方差的影響。最后通過一個4組件串聯(lián)系統(tǒng)實例，在考慮沖擊導(dǎo)致硬失效影響相關(guān)性和未考慮其相關(guān)性的對比試驗中，驗證了本文所提方法的有效性，體現(xiàn)了本文研究內(nèi)容對存在隨機沖擊影響的多部件退化設(shè)備壽命預(yù)測研究中具有一定的實用價值。

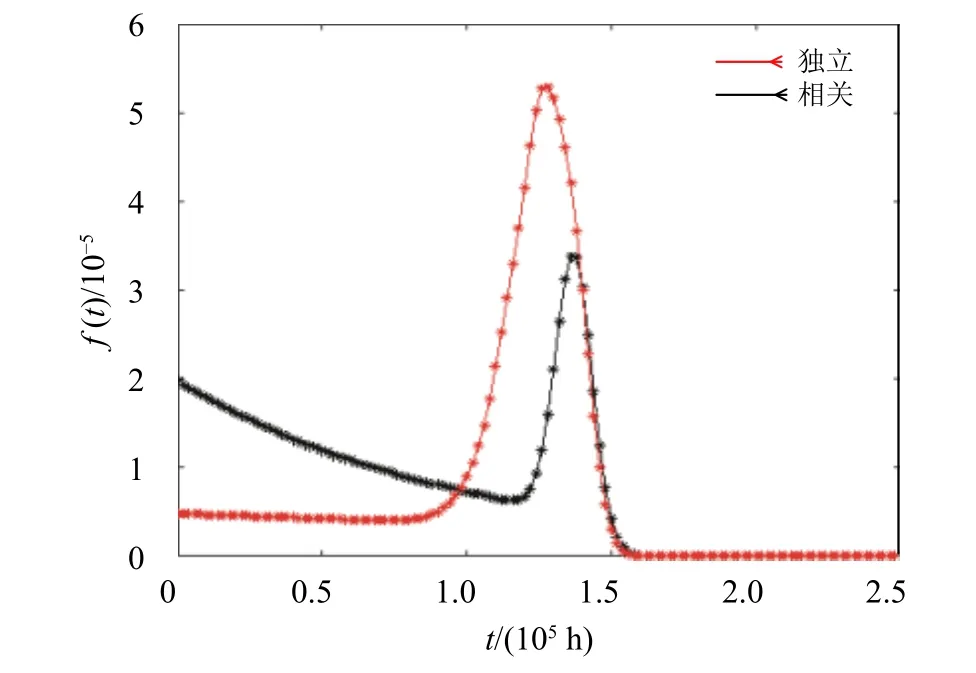
圖9 微機電系統(tǒng)壽命分布PDF