數學建模在生活中的應用
——以《備件最優配置模型》為例

王慧

(榆林市第三中學，陜西榆林 719000)

1 問題重述

系統由若干部件組成，只要一個部件出現故障，系統就不能正常工作。為提高系統可靠性，每個部件都裝有備件，一旦原部件出現故障，備件就自動進入系統。顯然，備件越多系統可靠性越大，但費用也越高。問題是在一定的費用下，如何配置各部件的備件使系統的可靠性最大。

問題一:由N個部件串接的系統，當部件

k

配置

j

個備件時，該部件正常工作的概率及費用已知，在總費用不超過定值的條件下，建立使系統的可靠性最大的模型。問題二:先設定總費用為10，若

n=

3且每個部件至多配置3個備件，部件

k

配置

j

個備件時正常工作的概率

p

及費用

c

如表1，求證如何配置各部件的備件系數使系統的可靠性最大。

2 問題分析

串聯系統是所有部件均可使用時才運轉正常的系統，它的可靠性為各部件可靠性的乘積。求系統的最大可靠性是一個典型的多階段決策問題。動態規劃是解決這樣一類最優化問題的專門計算方法，這類問題允許把它的過程(求解)分解為一系列的單級過程(步驟)。

而適用動態規劃的問題必須滿足最優化原理和無后效性。于是，我們有必要考察一下所求問題是否具有這兩點性質:

(1)最優化原理(最優子結構性質):不論過去狀態和決策如何，對前面的決策所形成的狀態而言，余下的諸決策必須構成最優策略。

這里，系統可靠性取決于各部件可靠性的乘積，可將系統配置的最優化問題轉化為各部件配置的優化問題。

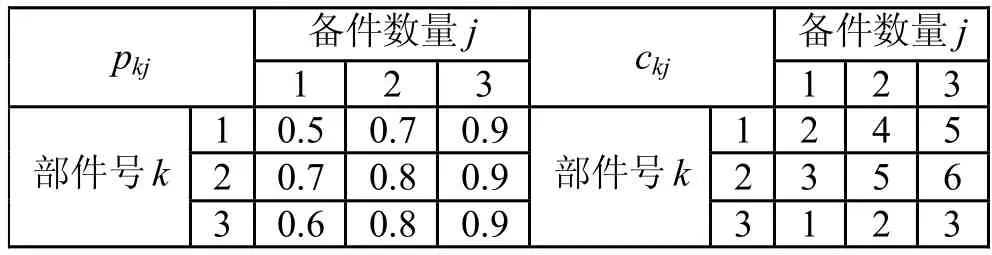
表1 給定費用和配件數后各部件正常工作的概率及費用表

(2)無后效性:某給定的階段狀態，它之前各階段的狀態無法直接影響它未來的決策，而只能通過當前的狀態。

該題表現為各部件的最優效率不影響下一部件的效率性能。

綜上所述，該系統可靠性優化問題完全可以用動態規劃的方法來解決。

2.1 問題一分析

經分析，該問題滿足動態規劃的諸要素，故可按以下步驟來建立動態規劃模型:

(1)把問題的過程劃分為恰當的若干個階段，引入階段變量；(2)正確選擇狀態變量，使它既能描述過程的演變，又能滿足無后效性；(3)確定決策變量及每個階段的允許決策集；(4)寫出狀態轉移方程；(5)指出階段指標及指標函數；(6)寫出最優函數。

2.2 問題二分析

在問題一的模型基礎上，結合必要數據，采用逆序解法進行求解即可。

3 模型假設

(1)系統的正常運作只取決于題給的部件；(2)備件配置后即發揮可靠性作用，不因意外因素停止運轉；(3)題給數據精確可靠。

4 定義與符號說明

k

:階段變量(

k

=1,2,…,

n

)；

x

:狀態變量；

c

:決策變量；

D

(

x

):允許決策集合；

M

:總費用；

p

(

x

,

c

):階段指標；

n

:部件號；

f

(

x

):最優值函數。

5 模型建立與求解

由問題分析可知，該問題可用動態規劃的方法來求解。

5.1 模型建立

按部件劃分階段，將它看做一個

n

階段決策問題。把系統第

k

個部件看作

k

個階段(

k

=1,2,…,

n

)，每個階段初可用于支配的費用是前面階段決策的結果，也是本階段決策的依據(示意圖如圖1)。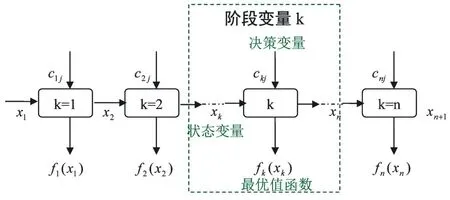

圖1 系統正態化圖

針對問題一，在總費用為

M

時，為使系統的可靠性最大，建立動態規劃模型:(1)階段變量

k

:按部件號將問題分為

k

個階段(

k

=1,2,…,

n

);(2)狀態變量

x

:表示第

k

個階段可用于支配的費用，其中

x

=

M

；(3)決策變量

c

:表示部件

k

配置

j

個備件時的費用；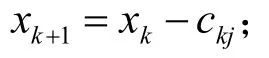

(6)階段指標

p

(

x

,

c

):表示當部件

k

配置

j

個部件時該部件可正常工作的概率；

(7)動態規劃基本方程:

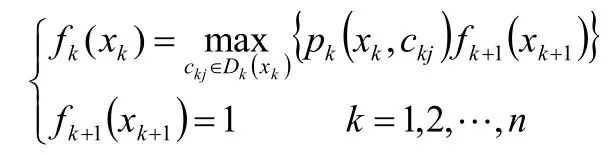
5.2 模型的實際應用

在問題一建立的模型中，取

n=

3且每個部件最多配置3個備件，總費用

M

=10。動態規劃基本方程為: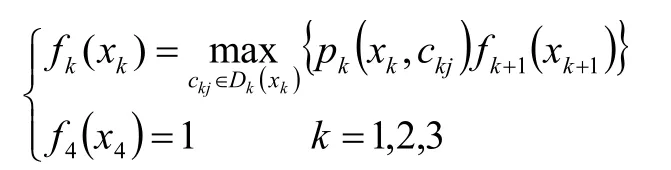

結合表1數據，對基本方程求解:

當

k

=1時，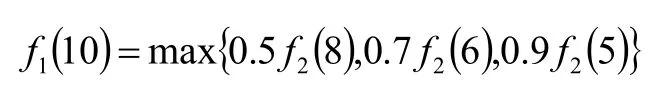

當

k

=2時，

當

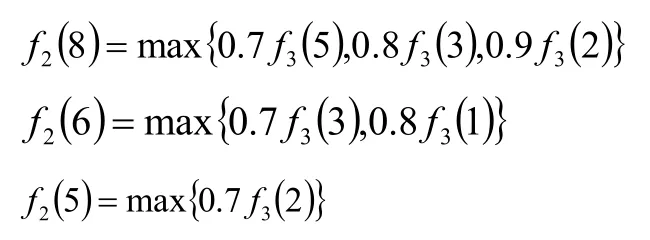
k

=3時，

按上面的順序反推算，可以得到:

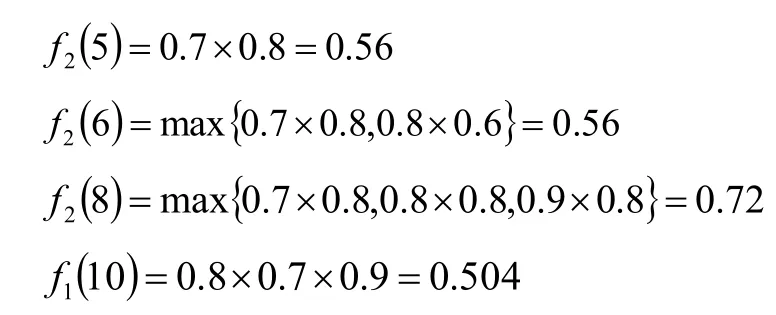
由以上求解可知，當總費用為10，部件1的備件數量為3，部件2的備件數量為1，部件3的備件數量為2時，系統的可靠性達最大，此時，系統正常工作的概率為0.504。

6 結果分析與檢驗

6.1 結果的程序驗算

對于模型的準確性驗證，可利用程序證明(見附錄程序6—1)。將動態規劃函數的程序錄入并計算后發現結果與我們的逆序解法完全一致，充分證明了模型的準確性和科學性。

6.2 模型合理性驗證

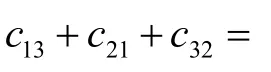
7 模型評價與推廣

本文運用動態規劃的重要思想，建立了給定費用下，系統配置的最優化模型。

7.1 模型評價

優點:(1)原理簡單，適用性廣；(2)在模型檢驗方面，針對該題數據少的實際情況，引入了遍歷搜索的辦法，更加精準的驗證了模型的科學性；(3)由于動態規劃方法反映了過程逐段演變的前后聯系和動態特征，在計算中可以利用實際知識和經驗提高求解效率。

缺點:(1)用數值方法求解時存在維數災；(2)對于較復雜的問題在選擇狀態、決策、確定狀態轉移規律等方面缺乏靈活性，這就帶來了應用上的局限性。

7.2 模型改進

當系統部件數目較大時，可借助計算機求取最優解。

7.3 模型推廣

本模型適用性較廣，可用于解決實際生活中的問題，例如，人員分配問題，最大受益問題以及最短路徑問題。