伯努利方程原理及其應用

吳明眼

（運城護理職業學院 山西 運城 044000）

1 伯努利方程原理

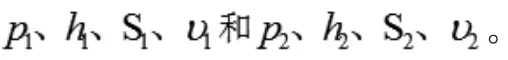
設a2b2與a1b1段液體的體積和質量為V和m。a1b1段液體的機械能為段液體的機械能為在Δt時間內a1a2段液體總的機械能的增量為

圖1 伯努利方程的推導

右側的力F2它對流體做負功，所做的功為

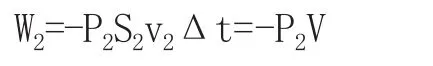
∴兩側外力對所研究液體所做的功為：

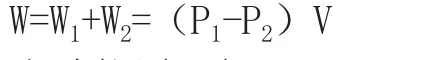
由功能原理得，ΔE=W

上式各項除以V并移項整理后得：

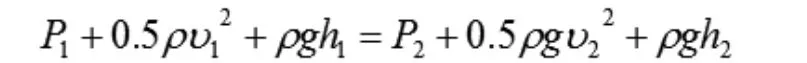
伯努利方程應用說明：嚴格地說，伯努利方程只適用于理想液體做穩定流動的情況。對于黏性較小的水、乙醇等液體或流動中密度變化很小的氣體，當它們作穩定流動時，伯努利方程仍近似成立[1]。

2 伯努利方程的應用

2.1 列車進站時，要站在兩米安全線外

在乘坐火車時，我們都會在站臺上看到一條長長的黃漆線，每當列車快進站時站臺工作人員都會要求乘客站在這條黃線后面。這是因為列車進站時速度都比較快，高速行駛的列車會帶動車廂兩側的空氣快速流動。根據伯努利方程可知，越靠近列車空氣流速越大，人體就會感到一股將人體推向列車的力。下面用伯努利方程定量計算靠近列車時，在人體兩側產生的壓力差的值，我們稱之為“風壓”。

由于空氣密度ρ和重度r的關系為r=ρg，因此有ρ=r/g。將ρ=r/g代入（1）式，得：

這就是風壓公式。在標準大氣壓下空氣重度r=0.0122599（kN/m3），重力加速度g=9.8m/s2，我們得到風速估計風壓的通用公式：

測算表明，一列時速為250公里的“子彈頭”開起來，在靠近列車車廂兩邊掀起的風速v高達26m/s。根據計算人體表面積許文生氏公式：

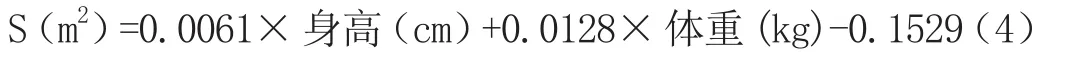
以某乘客身高170cm，體重65kg為例，根據（4）式，其體表面積計算S約為1.716m2。那么乘客在列車附近感受到時速為250公里的“子彈頭”的風的壓力F=ΔPS=362.5N，換算成公斤單位為37公斤。通過以上計算可知，人體靠近高速進站行駛的列車時會受到37公斤左右的推向列車的推力，這時非常危險的，很容易發生意外。因此，列車進站時，乘客要站在2米安全線外。

2.2 “香蕉球”原理

在足球比賽罰球時，我們經常看到球員將球踢出去之后球并不是沿著直線飛向球門，而是以弧形曲線飛向球門并進球。足球史上最著名的“香蕉球”球員非英國的貝克漢姆莫屬。貝克漢姆主罰任意球時，面對前方的人墻，往往不是直接把球射向球門，而是用右腳把球踢向球門外側，看似不會進球，但球往往在飛行的過程中最后卻意外拐彎進了球門，令守門員防不勝防。如果我們仔細觀察貝克漢姆射門時的右腳就會發現，他并不是用腳尖直接踢球的正中間，而是腳尖偏左側踢球的右側一邊。這樣踢球的結果就是足球在飛行過程中會逆時針旋轉著向前飛行，足球右側由于是逆風飛行，球面的旋轉方向和風向相反，空氣流線疏，足球左側球面的旋轉方向和風向相同，空氣流線密。這樣，球面左側的風速大于球面右側的風速，由伯努利方程可知，球飛行過程中空氣會產生向左的推力，足球的飛行軌跡活像一支香蕉，“香蕉球”的由來就是這樣產生的。用伯努利方程作如下分析：

式中，P1，P2為足球球面上對稱兩點的壓強，v0為空氣介質流速，v1為旋轉足球球面帶動與之相鄰的空氣的流速。

解上面方程式得：P1-P2=2ρv0v1

2.3 風掀屋頂

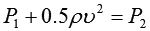
2.4 飛機的升力

飛機的重量非常大，飛機是如何能夠從地面上騰空而起的呢？飛機之所以能在空中飛行靠的就是飛行中一對機翼產生的升力。而飛機機翼一般都是上表面彎曲，下表面平坦，在飛機飛行過程中，機翼將迎面的風切割成了上下兩部分，在相同的時間里流過機翼上下表面空氣流走過相同位移但經過不同的路程，也就造成了機翼上、下表面空氣流速不同致使流過機翼下表面空氣速度小于流過機翼上表面空氣速度，機翼上下表面產生了向上的壓力差，所以飛機可以克服重力起飛并飛行。

下面定量計算飛機飛行時機翼上下表面產生的壓力差。為了計算的簡便，我們采用簡易模型的方法，把飛機的機翼橫截面設計成圓形的一部分（圖2）。設機翼上表面弧長對應的圓心角為π/3，流經飛機上表面氣流速度為v1，流經下表面氣流速度為v2，機翼上下表面壓強差為Δp。利用伯努利方程可得：。

圖2 飛機機翼橫截面圖

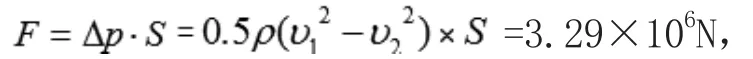
2.5 航行中的的兩船不能靠的太近[2]

當航行中的兩船彼此接近平行行駛時，兩船之間的水受到兩船的擠壓，兩船之間水的流線比船外側的流線更密一些，所以兩船之間水流速度比外部大一些，根據伯努利方程可知兩船之間的水壓比兩船外部的水壓小一些，這樣外部壓強較大的水壓就把兩船逐漸往一塊擠。因此，航行中的兩條船不能靠的太近，必須保持一定的距離。

2.6 風速太大導致人呼吸困難

當人們站在風口時，常會感到呼吸有略微的“困難”，用伯努利方程來解釋這是由于風口處空氣氣流較大，導致風口處氣壓略微降低，進而讓空氣進入人體肺部變得困難。

2.7 行駛的列車打開窗戶窗簾會向外飄

列車在高速行駛過程中，當打開窗戶時我們發現車窗窗簾總是呼啦啦往外飄。這是由于列車在高速行駛時車外兩側的風速遠遠大于車廂內部的氣流速度，根據伯努利方程可知車外兩側的氣壓遠遠小于車廂內部的氣壓，故打開車窗時，氣流會吹動窗簾往外飄。

2.8 在倒置的漏斗下放一個輕質小球不會掉落

在倒置的漏斗下放一個輕質小球，用手抵住，在小口中吹氣同時放開乒乓球，我們發現乒乓球不會掉落。這時由于吹氣時乒乓球上方的空氣流線密，流速大，下方的氣體流線疏，流速小，根據伯努利方程可知乒乓球下方的氣體大氣壓大于上方的大氣壓，故小球不會落下，只會在漏斗中跳躍。