風(fēng)沙對(duì)風(fēng)力機(jī)翼型繞流及其氣動(dòng)性能的影響

李仁年，趙振希，李德順，李銀然，陳 霞，于佳鑫

?

風(fēng)沙對(duì)風(fēng)力機(jī)翼型繞流及其氣動(dòng)性能的影響

李仁年1,2,3，趙振希1，李德順1,2,3，李銀然1,2,3，陳 霞1，于佳鑫1

（1. 蘭州理工大學(xué)能源與動(dòng)力工程學(xué)院，蘭州 730050；2. 甘肅省風(fēng)力機(jī)工程技術(shù)研究中心，蘭州 730050；3. 甘肅省流體機(jī)械及系統(tǒng)重點(diǎn)實(shí)驗(yàn)室，蘭州 730050）

中國(guó)西北地區(qū)風(fēng)能資源豐富，然而該地區(qū)經(jīng)常遭受沙塵天氣的侵襲。風(fēng)力機(jī)在強(qiáng)風(fēng)沙環(huán)境下運(yùn)行，其氣動(dòng)性能難免會(huì)受到沙塵的影響，并且其葉片會(huì)受到比較嚴(yán)重的磨損，導(dǎo)致機(jī)組的出力明顯下降。翼型作為風(fēng)力機(jī)葉片的基本組成單元，沙塵顆粒對(duì)翼型的繞流和氣動(dòng)特性的影響研究顯得尤為必要。該文利用雷諾平均Navier-Stokes方程-大渦模擬（large eddy simulation）混合方法中的延遲分離渦模擬方法，模擬了NREL S809翼型在風(fēng)沙環(huán)境下的流動(dòng)特性，將不同顆粒直徑條件下翼型周圍的繞流情況和翼型的氣動(dòng)性能進(jìn)行了對(duì)比，研究了空氣中的顆粒對(duì)風(fēng)力機(jī)翼型繞流及其氣動(dòng)性能的影響規(guī)律。結(jié)果表明，6.1°攻角時(shí)，顆粒對(duì)翼型繞流和升力系數(shù)的影響較小，但仍會(huì)使翼型的升力系數(shù)略微降低。隨著顆粒直徑的增大，翼型的升力系數(shù)先減小再增大，其中顆粒直徑為20m時(shí)達(dá)到最小值。當(dāng)顆粒直徑為150m時(shí)，其升力系數(shù)仍小于潔凈空氣下的升力系數(shù)，但兩者已十分接近。8.2°攻角時(shí)，不同直徑顆粒對(duì)翼型繞流具有不同程度的影響，當(dāng)顆粒直徑小于20m時(shí)，顆粒的跟隨性較好，顆粒緊隨氣相運(yùn)動(dòng)，對(duì)翼型繞流的影響較小；當(dāng)顆粒直徑為20m時(shí)顆粒對(duì)翼型繞流造成了極大的影響，如分離點(diǎn)提前、出現(xiàn)展向流動(dòng)；當(dāng)顆粒直徑大于20m后，隨著顆粒直徑的繼續(xù)增大，顆粒的慣性力變強(qiáng)，顆粒逐漸獨(dú)立于氣相運(yùn)動(dòng)，對(duì)翼型繞流的影響也逐漸減弱。升力系數(shù)隨顆粒直徑的變化趨勢(shì)和小攻角時(shí)相同，但變化幅度變大，升力系數(shù)最小時(shí)比潔凈空氣時(shí)減少了7.9%。該文可為不同顆粒直徑的風(fēng)沙環(huán)境下顆粒對(duì)翼型周圍繞流流場(chǎng)及其對(duì)翼型升力系數(shù)影響等相關(guān)研究提供參考。

風(fēng)力機(jī)；風(fēng)能；計(jì)算機(jī)仿真；延遲分離渦模擬；翼型；顆粒直徑；翼型繞流；流動(dòng)分離

0 引 言

風(fēng)力機(jī)在工作過(guò)程中會(huì)受到空氣中顆粒的影響，造成氣動(dòng)力和載荷的變化以及磨損。同時(shí)，由于固相的加入，改變了翼型周圍的繞流流動(dòng)，對(duì)翼型的氣動(dòng)性能造成不可忽視的影響，因此針對(duì)風(fēng)沙環(huán)境下翼型流場(chǎng)的研究很有必要。Khalfallah等[1]對(duì)赫爾格達(dá)風(fēng)電場(chǎng)內(nèi)風(fēng)電機(jī)組進(jìn)行了長(zhǎng)期的監(jiān)測(cè)，結(jié)果表明，由于沙塵對(duì)風(fēng)力機(jī)葉片的沖蝕磨損作用，風(fēng)力發(fā)電機(jī)組運(yùn)行3個(gè)月后，其出力出現(xiàn)明顯的下降，下降率近15%，且隨著運(yùn)行時(shí)間的增長(zhǎng)，下降幅度加劇；Khakpour[2]研究了風(fēng)沙環(huán)境下翼型的氣動(dòng)性能；李德順等[3-4]研究了DU96-W-180翼型前緣不同磨損階段下的氣動(dòng)性能，結(jié)果表明前緣發(fā)生脫層后翼型的氣動(dòng)性能顯著降低；采用可實(shí)現(xiàn)湍流模型和離散相模型(discrete phase model, DPM)研究了風(fēng)力機(jī)翼型的升阻力系數(shù)和靜壓隨沙塵質(zhì)量濃度變化的規(guī)律，以及不同風(fēng)沙環(huán)境下風(fēng)輪的轉(zhuǎn)矩特性。但是這些研究都是以二維翼型為研究對(duì)象并且采用定常的方法計(jì)算，而顆粒對(duì)翼型周圍流動(dòng)結(jié)構(gòu)的影響是十分復(fù)雜的并且具有很強(qiáng)的非定常特性，特別是在攻角較大的情況下。

目前針對(duì)風(fēng)力機(jī)翼型的氣固兩相流研究較少，但是針對(duì)圓柱繞流的相關(guān)研究已初具規(guī)模。羅坤等[5]利用PIV技術(shù)研究了氣固兩相圓柱繞流的近場(chǎng)特性；樊建人等[6]利用直接數(shù)值模擬研究了氣固兩相圓柱繞流中顆粒的擴(kuò)散運(yùn)動(dòng)；劉洪濤等[7]研究了圓柱繞流背風(fēng)區(qū)不同直徑顆粒的運(yùn)動(dòng)特性；李文春等[8]針對(duì)三維氣固兩相圓柱繞流進(jìn)行了數(shù)值模擬，分析了不同Stokes數(shù)的顆粒在渦作用下的擴(kuò)散；嵇峰等[9]進(jìn)行了三維數(shù)值模擬，發(fā)現(xiàn)顆粒在圓柱展向上的擴(kuò)散也和顆粒的Stokes數(shù)有關(guān)，相同雷諾數(shù)下，顆粒Stokes數(shù)越小，展向擴(kuò)散越大，流動(dòng)越不穩(wěn)定；黃遠(yuǎn)東等[10]針對(duì)液固兩相圓柱繞流研究了顆粒的擴(kuò)散。結(jié)合針對(duì)圓柱繞流的相關(guān)研究，說(shuō)明了針對(duì)翼型的兩相流研究也應(yīng)該采用三維、非定常的方法。

當(dāng)前經(jīng)常使用的湍流模型是求解雷諾平均Navier- Stokes（reynolds average navier-stokes, RANS）方程，該方法可以準(zhǔn)確預(yù)測(cè)附著流和小分離時(shí)的氣動(dòng)特性。但該方法對(duì)顆粒引入后的翼型流場(chǎng)其預(yù)測(cè)精度急劇下降，預(yù)測(cè)結(jié)果不真實(shí)。大渦模擬（large eddy simulation, LES）通過(guò)模化小尺度渦，直接計(jì)算大渦，在非定常及分離流動(dòng)問(wèn)題上體現(xiàn)出明顯的優(yōu)勢(shì)，然而該方法對(duì)網(wǎng)格的要求十分苛刻，且尚不成熟的近壁面模型制約了LES方法的應(yīng)用。近年來(lái)興起的RANS-LES混合方法，結(jié)合了RANS和LES2種方法的優(yōu)點(diǎn)。其中包括Spalart等[11-13]提出的分離渦方法（detached eddy simulation，DES），采用RANS方法高效準(zhǔn)確地模擬近壁區(qū)域的高頻小尺度運(yùn)動(dòng)，同時(shí)采用LES方法模擬低頻大尺度占主導(dǎo)的非定常分離流動(dòng)區(qū)域。Strelets[14]結(jié)合SST湍流模型發(fā)展了SST-DES模型。Menter等[15]改進(jìn)了SST-DES模型并提出了給出了一種延遲分離渦模擬（delay detached eddy simulation，DDES），此方法解決了近壁面網(wǎng)格較密時(shí)，LES方法提前啟動(dòng)的問(wèn)題，以保證邊界層內(nèi)完全使用RANS方法。

胡偶等[16]將SST-DDES混合模型應(yīng)用在大分離流動(dòng)的分析中。劉周等[17]研究了翼型大攻角非定常分離流動(dòng)。劉健等[18]基于iDDES模型研究了雙三角翼大攻角的渦破特征。趙偉文等[19]利用DES模型研究了串列雙圓柱繞流的問(wèn)題。夏明等[20]采用DDES模型模擬了Gurney襟翼的分離流動(dòng)，得到滿意的效果。白俊強(qiáng)等[21]模擬了鈍前緣三角翼在大攻角下的流動(dòng)。王翔宇等[22]基于SST-DES模型在小分離流動(dòng)中的表現(xiàn)，提出了改進(jìn)方法，以減小RANS區(qū)對(duì)LES區(qū)的影響。靳瑤等[23]針對(duì)=3 900的圓柱繞流進(jìn)行了數(shù)值模擬并與試驗(yàn)結(jié)果對(duì)比，發(fā)現(xiàn)DDES模擬可捕捉豐富的流場(chǎng)結(jié)構(gòu)。劉若陽(yáng)等[24-26]利用DDES模型對(duì)葉柵以及翼型繞流問(wèn)題進(jìn)行了大量研究。

本文選用基于SST湍流模型的DDES方法，對(duì)美國(guó)風(fēng)力機(jī)翼型NREL S809[27]在風(fēng)沙環(huán)境下進(jìn)行數(shù)值模擬，研究不同直徑顆粒對(duì)翼型繞流流場(chǎng)及其氣動(dòng)性能的影響。

1 數(shù)值方法

1.1 數(shù)學(xué)模型及計(jì)算網(wǎng)格

本文以NREL S809三維直葉片為研究對(duì)象，其相對(duì)厚度21%，弦長(zhǎng)1 m，展向拉伸0.5倍弦長(zhǎng)。采用C型計(jì)算域。以翼型前緣點(diǎn)為原點(diǎn)建立坐標(biāo)系，尾緣方向?yàn)榉较颍灰硇驼瓜驗(yàn)榉较颍硎疽硇拖议L(zhǎng)。在方向，從翼型前緣拓展到弦長(zhǎng)的16倍，從翼型尾緣拓展到弦長(zhǎng)的20倍；在方向，正負(fù)兩方向拓展到弦長(zhǎng)的16倍。

本文采用歐拉-拉格朗日方法，空氣作為連續(xù)相基于歐拉框架通過(guò)SST-DDES湍流模型進(jìn)行求解；固相顆粒作為離散相基于拉格朗日框架通過(guò)離散相模型求解。顆粒噴射入口采用surface類型，噴射入口距葉片前緣5倍弦長(zhǎng)，面積0.5 m×6 m，顆粒軌道數(shù)為960×80，共76 800。

采用結(jié)構(gòu)化網(wǎng)格，首層網(wǎng)格厚度取0.012 mm，其無(wú)量綱高度+小于1，翼型表面有250個(gè)點(diǎn)，展向布置50個(gè)點(diǎn)，使得D≈D。顆粒入射方向和速度與氣相一致，時(shí)間步長(zhǎng)取0.000 4 s。計(jì)算域和近壁面網(wǎng)格如圖1所示。

1.2 計(jì)算條件與可靠性驗(yàn)證

進(jìn)口采用速度進(jìn)口邊界，出口采用壓力出口邊界，翼型展向兩側(cè)邊界設(shè)置為對(duì)稱邊界。雷諾數(shù)為=106，風(fēng)速為14.61 m/s。顆粒密度為1 550 kg/m3，顆粒入射質(zhì)量流率取為空氣質(zhì)量流率的0.01，為0.537 kg/s。換算成顆粒質(zhì)量濃度為6.13′106g/m3，對(duì)應(yīng)體積濃度為3.95′10-6（屬于強(qiáng)沙塵暴）[28]。計(jì)算采用SIMPLEC算法，動(dòng)量和湍動(dòng)能均采用二階迎風(fēng)格式。根據(jù)文獻(xiàn)[29-30]中的方法修正模型系數(shù)1和*，提高近壁面RANS區(qū)的模擬精度。圖2為潔凈空氣條件下不同攻角下的升力系數(shù)與文獻(xiàn)[31]中DUT大學(xué)（Delft University of Technology）利用低速低湍流度風(fēng)洞得到的試驗(yàn)數(shù)據(jù)進(jìn)行對(duì)比，模擬結(jié)果與試驗(yàn)數(shù)據(jù)吻合度較好，14.2°攻角時(shí)升力系數(shù)誤差達(dá)到最大，為3.3%。

注：c為弦長(zhǎng)；x方向?yàn)闄M坐標(biāo)正方向。

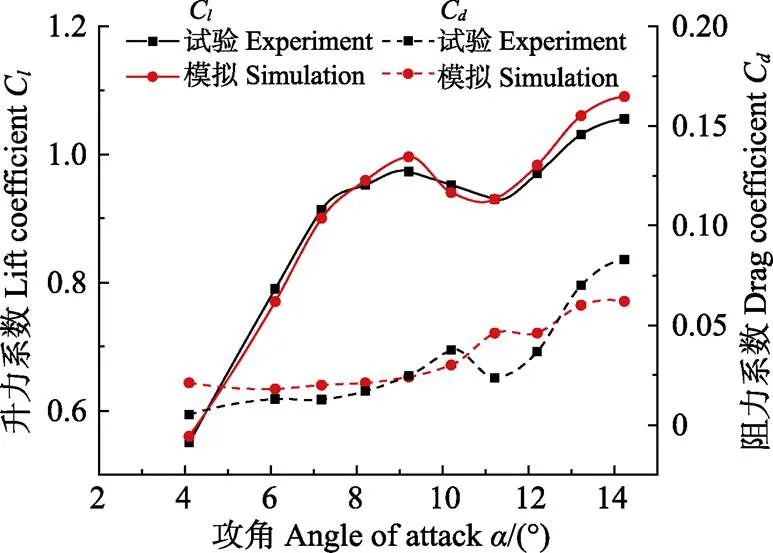
圖2 潔凈空氣條件下升力、阻力系數(shù)模擬數(shù)據(jù)與試驗(yàn)數(shù)據(jù)對(duì)比圖

對(duì)于DPM模型，通過(guò)對(duì)氣固兩相流條件下的圓柱繞流進(jìn)行數(shù)值模擬，通過(guò)分析顆粒的運(yùn)動(dòng)軌跡，并與羅坤等[5]的圖像測(cè)速（particle image velocimetry）試驗(yàn)進(jìn)行比較。工況設(shè)置與試驗(yàn)條件相同，質(zhì)量濃度比為10%，顆粒Stokes數(shù)為0.98，圓柱直徑d為0.01 m。結(jié)果如圖3所示，離散相模型可以模擬出沙塵顆粒隨空氣圓柱繞流時(shí)的運(yùn)動(dòng)特性，但是對(duì)比真實(shí)情況，數(shù)值模擬的耗散較快，導(dǎo)致顆粒運(yùn)動(dòng)到圓柱后較遠(yuǎn)時(shí)模擬結(jié)果與試驗(yàn)結(jié)果差異較大。圖4為距離圓柱后x/d=2截面上的顆粒平均速度試驗(yàn)結(jié)果和模擬結(jié)果對(duì)比，可以看出在近尾流區(qū)域模擬結(jié)果與試驗(yàn)結(jié)果吻合度較高[32]。因此，認(rèn)為本文的模擬方法可靠。

圖3 模擬顆粒運(yùn)動(dòng)軌跡與試驗(yàn)PIV圖像對(duì)比

注：U0為來(lái)流速度；U為顆粒速度；y/dc表示縱向位置；dc為圓柱直徑。

2 結(jié)果及分析

2.1 顆粒對(duì)翼型繞流的影響

圖5是6.1°攻角時(shí)，潔凈空氣和不同直徑顆粒條件下的翼型吸力面極限流線圖，可以看出在此攻角時(shí)，顆粒對(duì)翼型表面的繞流情況沒(méi)有明顯的影響，翼型表面沒(méi)有發(fā)生流動(dòng)分離，流動(dòng)狀態(tài)穩(wěn)定且可以簡(jiǎn)化為二維流動(dòng)。

注：d為顆粒直徑。

當(dāng)攻角增大到8.2°時(shí)，從潔凈空氣下翼型表面極限流線，翼型吸力面從前緣起0.607處將發(fā)生流動(dòng)分離，并在分離點(diǎn)后產(chǎn)生了分離泡，流動(dòng)狀態(tài)穩(wěn)定，依然可以視為二維流動(dòng)，如圖6所示。

圖7為在不同直徑顆粒條件下，翼型吸力面的極限流線圖，從圖中可以看出8.2°攻角時(shí)，顆粒對(duì)翼型表面繞流的影響非常大。當(dāng)加載10m直徑的顆粒時(shí)，流動(dòng)開(kāi)始發(fā)生變化，沿展向每個(gè)截面上分離點(diǎn)的位置均不同，平均分離位置略微朝翼型前緣移動(dòng)了0.049，即分離點(diǎn)在0.558處，并且分離渦出現(xiàn)了微小的展向流動(dòng)，流動(dòng)狀態(tài)已從簡(jiǎn)單的二維流動(dòng)變成了三維流動(dòng)；顆粒直徑增大到20m，可以看出翼型表面的流動(dòng)狀態(tài)發(fā)生了非常大的變化，分離點(diǎn)大幅度前移，平均分離位置大幅度向翼型前緣移動(dòng)了0.094，即分離點(diǎn)在0.512處，并且沿展向每個(gè)截面上分離的位置均不同，氣流經(jīng)過(guò)分離點(diǎn)后的流動(dòng)狀態(tài)為復(fù)雜的三維流動(dòng)；當(dāng)顆粒直徑為30m時(shí)，翼型表面的繞流狀態(tài)趨于穩(wěn)定，分離點(diǎn)后移，三維流動(dòng)現(xiàn)象減弱。隨著顆粒直徑的繼續(xù)增大，翼型表面的流動(dòng)狀態(tài)愈發(fā)趨于穩(wěn)定，三維流動(dòng)現(xiàn)象減弱。當(dāng)顆粒直徑為50m時(shí)三維流動(dòng)現(xiàn)象基本消失；當(dāng)顆粒直徑為100m時(shí)分離點(diǎn)位置向潔凈空氣時(shí)的分離位置移動(dòng)。當(dāng)顆粒直徑為150m時(shí)，分離點(diǎn)基本與潔凈空氣狀態(tài)下的分離點(diǎn)重合，相較潔凈空氣下的分離點(diǎn)仍向前緣移動(dòng)了0.01。

圖6 8.2°攻角時(shí)潔凈空氣下極限流線和中間截面處流線

圖7 8.2°攻角時(shí)不同直徑顆粒條件下翼型吸力面極限流線

為了更好地揭示顆粒對(duì)翼型周圍繞流流場(chǎng)的影響，在翼型尾緣和翼型尾緣后0.5處分別建立截面，圖8為潔凈空氣和不同直徑顆粒條件下翼型周圍三維流線和截面上的展向速度云圖。圖9是各工況下翼型展向0.5倍截面處顆粒質(zhì)量分布圖和三維流線圖。

由圖8可知，潔凈空氣時(shí)，在翼型尾流區(qū)存在微小的展向流動(dòng)，速度較小可忽略；當(dāng)加載10m顆粒時(shí)，翼型周圍的流線出現(xiàn)了小幅度的擾動(dòng)，從翼型尾緣處的展向速度云圖可知，氣流在尾流區(qū)有微弱的展向速度，在氣流經(jīng)過(guò)翼型之后展向速度逐漸減弱，在尾緣后0.5處基本消失；加載20m直徑顆粒時(shí)，翼型周圍流線出現(xiàn)了大幅度的擾動(dòng)，氣流在尾流區(qū)具有較大的展向速度，且在翼型尾緣后0.5處依然較大；隨著顆粒直徑的增大，流動(dòng)趨于穩(wěn)定，展向速度減弱。當(dāng)顆粒直徑為150m時(shí)，流動(dòng)狀態(tài)基本與潔凈空氣時(shí)無(wú)異，但展向速度仍大于潔凈空氣時(shí)的展向速度。

當(dāng)氣相流經(jīng)翼型表面時(shí)，在翼型的前駐點(diǎn)分為兩股，沿著上、下翼面流向翼型尾緣。此時(shí)的流動(dòng)狀態(tài)明顯區(qū)別于來(lái)流的流動(dòng)狀態(tài)[33]。同時(shí)，空氣中的沙塵顆粒響應(yīng)氣相流動(dòng)狀態(tài)改變的時(shí)間稱為顆粒的松弛時(shí)間，過(guò)程中伴隨著顆粒與氣相之間的動(dòng)量交換。顆粒的松弛時(shí)間為τ=ρd2/18，為氣相流動(dòng)的特征時(shí)間，其中ρ和d分別為顆粒的密度和直徑；和為翼型的弦長(zhǎng)和來(lái)流風(fēng)速，顆粒的Stokes數(shù)=τ/可以用來(lái)衡量顆粒的慣性[34]。越大，顆粒的慣性力越強(qiáng)，顆粒需要更長(zhǎng)的時(shí)間來(lái)響應(yīng)流場(chǎng)的變化；越小，顆粒的跟隨性越好，顆粒響應(yīng)流場(chǎng)變化所需的時(shí)間越短。綜上，顆粒對(duì)翼型繞流流場(chǎng)的影響非常大。這是顆粒與氣相之間的動(dòng)量交換引起的。

圖8 8.2°攻角時(shí)不同直徑顆粒條件下翼型周圍三維流線和截面上的展向速度云圖

圖9 8.2°攻角時(shí)不同直徑顆粒條件下翼型中間截面上顆粒質(zhì)量濃度分布圖和三維流線

由圖9可知，當(dāng)顆粒直徑為10m時(shí)，較小。顆粒主要分布在分離區(qū)邊緣，表現(xiàn)出較強(qiáng)的跟隨性。慣性力的作用很小，氣流挾顆粒繞過(guò)翼型時(shí)發(fā)生了微弱的動(dòng)量交換，導(dǎo)致出現(xiàn)了微弱的三維流動(dòng)現(xiàn)象并且分離點(diǎn)略微前移，但這并不足以對(duì)整個(gè)流場(chǎng)產(chǎn)生劇烈的影響；當(dāng)顆粒直徑為20m時(shí)，顆粒不再緊隨氣相運(yùn)動(dòng)，大量顆粒進(jìn)入了尾流區(qū)，并改變了翼型附近的流場(chǎng)，說(shuō)明此時(shí)氣流與顆粒之間發(fā)生了很強(qiáng)的動(dòng)量交換。這是因?yàn)閷?duì)比10m直徑的顆粒，20m直徑顆粒的數(shù)較大，慣性力的作用較強(qiáng)，因此氣流挾顆粒繞流過(guò)翼型時(shí)與顆粒發(fā)生了劇烈的動(dòng)量交換，從而導(dǎo)致了整個(gè)流場(chǎng)的變化，表現(xiàn)出三維流動(dòng)現(xiàn)象并且分離點(diǎn)大幅度前移。

顆粒直徑為30m時(shí)，可以看出此時(shí)流場(chǎng)情況已經(jīng)開(kāi)始逐漸恢復(fù)；當(dāng)顆粒直徑增大到50m，流動(dòng)狀態(tài)開(kāi)始趨于穩(wěn)定，觀察顆粒質(zhì)量分布和翼型周圍流線可以發(fā)現(xiàn)此時(shí)顆粒的流動(dòng)基本獨(dú)立于氣流，這是因?yàn)轭w粒直徑增大慣性力已經(jīng)開(kāi)始占主導(dǎo)作用，氣流對(duì)于顆粒的作用力基本可以忽略；顆粒直徑為150m時(shí)，由于慣性力作用，此時(shí)顆粒已經(jīng)完全獨(dú)立于氣相運(yùn)動(dòng)，從此工況下的三維流線中，可知?dú)饬骶o貼翼型表面流動(dòng)，與潔凈空氣狀態(tài)下的流動(dòng)狀態(tài)幾乎一致。對(duì)比不同時(shí)刻不同截面的三維流線圖和顆粒質(zhì)量分布圖，發(fā)現(xiàn)當(dāng)顆粒大于50m時(shí)和潔凈空氣條件時(shí)流動(dòng)沒(méi)有體現(xiàn)出非定常現(xiàn)象。

2.2 顆粒對(duì)翼型氣動(dòng)性能的影響

顆粒對(duì)翼型繞流的影響反映到對(duì)翼型氣動(dòng)性能的影響上。圖10是潔凈空氣和不同直徑顆粒條件下翼型表面壓力系數(shù)圖。

由圖10可知，在流動(dòng)發(fā)生分離之前，風(fēng)沙環(huán)境下翼型壓力面的壓力系數(shù)均小于潔凈空氣下壓力面的壓力系數(shù)，同時(shí)吸力面的壓力系數(shù)顆粒也均小于潔凈空氣下的壓力系數(shù)；流動(dòng)發(fā)生分離之后，風(fēng)沙環(huán)境下壓力面的壓力系數(shù)仍小于潔凈空氣下壓力面的壓力系數(shù)，當(dāng)流動(dòng)發(fā)生分離后，風(fēng)沙環(huán)境下吸力面的壓力系數(shù)明顯大于潔凈空氣時(shí)吸力面的壓力系數(shù)，并且在20m直徑顆粒條件下達(dá)到最大值，這與流動(dòng)尚未發(fā)生分離時(shí)的規(guī)律恰好相反，這說(shuō)明在翼型吸力面的分離區(qū)，顆粒的加入反而會(huì)提高壓力系數(shù)。通過(guò)對(duì)比不同條件下翼型表面的壓力系數(shù)，可以發(fā)現(xiàn)隨著顆粒直徑的增大，壓力面和吸力面的壓力系數(shù)變小，當(dāng)顆粒直徑為20m時(shí)達(dá)到最小值，隨后隨著顆粒直徑的增大逐漸朝潔凈空氣時(shí)的圧力曲線靠攏，當(dāng)顆粒直徑為150m時(shí)，其壓力系數(shù)曲線基本與潔凈空氣時(shí)無(wú)異。

注： x/c表示橫向位置，見(jiàn)圖1a。

圖11是S809翼型的升力系數(shù)隨顆粒直徑變化曲線。可以看出當(dāng)潔凈空氣中加入小直徑顆粒，翼型升力系數(shù)變小，顆粒直徑為20m時(shí)升力系數(shù)達(dá)到最小值。6.1°攻角時(shí)減小了3.9%，隨后隨著顆粒直徑的增大，翼型升力系數(shù)將逐漸增大，但還是比潔凈空氣時(shí)小，顆粒直徑為150m時(shí)的升力系數(shù)比潔凈空氣時(shí)減小了1.3%。當(dāng)攻角為8.2°時(shí)，總體趨勢(shì)跟6.1°攻角時(shí)一樣，在20m直徑顆粒條件下升力系數(shù)達(dá)到最小值，比潔凈空氣時(shí)減小了7.9%，顆粒直徑為150m時(shí)的升力系數(shù)比潔凈空氣時(shí)減小了0.77%。相較沒(méi)有發(fā)生流動(dòng)分離的6.1°攻角，8.2°攻角時(shí)升力系數(shù)的變化幅度更大。

圖11 升力系數(shù)隨顆粒直徑變化

3 結(jié)論與討論

本文基于RANS-LES混合方法中的SST-DDES方法，研究了風(fēng)力機(jī)翼型在不同顆粒直徑的風(fēng)沙環(huán)境下顆粒對(duì)翼型周圍繞流流場(chǎng)及其對(duì)翼型升力系數(shù)的影響，結(jié)論如下：

1）顆粒對(duì)翼型繞流流場(chǎng)有不可忽視的影響。當(dāng)攻角較小時(shí)，顆粒對(duì)流場(chǎng)的影響較小，但仍使翼型的升力系數(shù)發(fā)生微小的變化；當(dāng)攻角較大時(shí)（8.2°），顆粒對(duì)翼型繞流流場(chǎng)的影響較大，體現(xiàn)在分離點(diǎn)提前、出現(xiàn)展向流動(dòng)、尾渦變大。當(dāng)顆粒直徑不同時(shí)，翼型繞流情況也不同。當(dāng)顆粒直徑小于20m時(shí)，隨著顆粒直徑的增大，翼型吸力面分離點(diǎn)提前，三維流動(dòng)現(xiàn)象出現(xiàn)并逐漸加劇；當(dāng)顆粒直徑大于20m后，隨著顆粒直徑的增大，翼型繞流情況逐漸恢復(fù)，三維流動(dòng)現(xiàn)象減弱、分離點(diǎn)后移。當(dāng)顆粒直徑為150m時(shí)，其繞流情況基本與潔凈空氣時(shí)相同。

2）當(dāng)顆粒直徑小于20m時(shí)，翼型的升力系數(shù)隨著顆粒直徑的增大而減小。當(dāng)顆粒直徑為20m時(shí)，翼型的升力系數(shù)達(dá)到最小值：6.1°攻角時(shí)相對(duì)于潔凈空氣條件下的升力系數(shù)減小了3.9%；而8.2°攻角時(shí)則下降了7.9%。當(dāng)顆粒直徑大于20m后，翼型的升力系數(shù)隨著顆粒直徑的增大而增大，但當(dāng)顆粒直徑增大到150m時(shí)仍比潔凈空氣時(shí)的升力系數(shù)小。

3）當(dāng)顆粒直徑小于20m時(shí)，顆粒的慣性力較弱，顆粒緊隨著氣相運(yùn)動(dòng)，表現(xiàn)出良好的跟隨性，對(duì)翼型繞流流場(chǎng)的影響較小。隨著顆粒直徑的增大，顆粒對(duì)翼型繞流流場(chǎng)的影響越來(lái)越大；當(dāng)顆粒直徑為20m時(shí)，此時(shí)顆粒的慣性力較強(qiáng)，顆粒與氣相之間存在劇烈的動(dòng)量交換，顆粒對(duì)翼型繞流流場(chǎng)的影響最為嚴(yán)重；當(dāng)顆粒直徑大于20m后，隨著顆粒直徑的增大，顆粒的慣性力越來(lái)越強(qiáng)，固相幾乎獨(dú)立于氣相運(yùn)動(dòng)，對(duì)翼型繞流流場(chǎng)的影響逐漸減弱。

本文在同一顆粒質(zhì)量濃度下，研究了不同直徑顆粒對(duì)翼型繞流及其氣動(dòng)性能的影響，后續(xù)將進(jìn)一步研究系統(tǒng)顆粒數(shù)翼型繞流及其氣動(dòng)性能隨攻角和顆粒質(zhì)量濃度的變化規(guī)律。

[1] Khalfallah M G, and Koliub A M. Effect of dust on the performance of wind turbines[J]. Desalination, 2007, 209(1): 209－222.

[2] Khakpour Y. Aerodynamic Performance of Wind Turbine Blades in Dusty Environments[D]. Chicago: Illinois Institute of Technology, 2007.

[3] 李德順，王成澤，李銀然，等. 葉片前緣磨損形貌特征對(duì)風(fēng)力機(jī)翼型氣動(dòng)性能的影響[J]. 農(nóng)業(yè)工程學(xué)報(bào)，2017，33(22)：269－275. Li Deshun, Wang Chengze, Li Yinran, et al. Influence of blade leading edge erosion features on aerodynamics characteristics of wind turbine airfoil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(22): 269－275. (in Chinese with English abstract)

[4] 李德順，董麟，劉宜，等. 風(fēng)沙環(huán)境對(duì)NACA-0012翼型氣動(dòng)性能的影響[J]. 蘭州理工大學(xué)學(xué)報(bào)，2015，41(6)：54－59. Li Deshun, Dong Lin, Liu Yi, et al. Effect of sand-laden wind environment on aerodynamic characteristics of airfoil NACA-0012 [J]. Journal of Lanzhou University of Technology, 2015, 41(6): 54－59. (in Chinese with English abstract)

[5] 羅坤，陳松，蔡丹云，等. 氣固兩相圓柱繞流近場(chǎng)特性的實(shí)驗(yàn)研究[J]. 中國(guó)電機(jī)工程學(xué)報(bào)，2006，26(24)：116－120. Luo Kun, Chen Song, Cai Danyun, et al. Experimental study of flow characteristics in the near field of gas-solid two-phase circular cylinder wakes[J]. Proceedings of the CSEE, 2006, 26(24): 116－120. (in Chinese with English abstract)

[6] 樊建人，胡桂林，姚軍，等. 氣固兩相圓柱繞流的直接數(shù)值模擬[J]. 工程熱物理學(xué)報(bào)，2003(3)：433－436. Fan Jianren, Hu Guilin, Yao Jun, et al. Direct numerical simulation of particle dispersion in the temporal wake of a circular cylinde[J]. Journal of Engineering Thermophysics, 2003(3): 433－436. (in Chinese with English abstract)

[7] 劉洪濤，張力，陳艷容. 氣固兩相圓柱繞流背風(fēng)區(qū)顆粒的運(yùn)動(dòng)特性[J]. 重慶大學(xué)學(xué)報(bào)，2010，33(4)：54－59. Liu Hongtao, Zhang Li, Chen Yanrong. Investigations of the particle motion characteristics in the gas-solid two-phase wake of leeward side circular cylinder[J]. Journal of Chongqing University, 2010, 33(4): 54－59. (in Chinese with English abstract)

[8] 李文春，金晗輝，任安祿，等. 氣固兩相三維圓柱繞流的直接數(shù)值模擬[J]. 工程熱物理學(xué)報(bào)，2006，27(5)：808－810. Li Wenchun, Jin Hanhui, Ren Anlu, et al. Direct numerical simulation of gas-solid two-phase 3d wake of a circular cylinder[J]. Journal of Engineering Thermophysics, 2006, 27(5): 808－810. (in Chinese with English abstract)

[9] 嵇峰，樊建人，任安祿，等. 氣固兩相圓柱繞流轉(zhuǎn)捩兩種模式的三維直接數(shù)值模擬[J]. 中國(guó)電機(jī)工程學(xué)報(bào)，2006，26(23)：55－60. Ji Feng, Fan Jianren, Ren Anlu, et al. Three-dimensional direct numerical simulation of circular cylinder wake transition in gas particle flow[J]. Proceedings of the CSEE, 2006, 26(23): 55－60. (in Chinese with English abstract)

[10] 黃遠(yuǎn)東，吳文權(quán). 液固兩相圓柱繞流尾跡內(nèi)顆粒擴(kuò)散分布的離散渦數(shù)值研究[J]. 應(yīng)用數(shù)學(xué)和力學(xué)，2006，27(4): 477－483. Huang Yuandong, Wu Wenquan. Numerical study of particle distribution in wake of liquid-particle flows past a circular cylinder using discrete vortex method[J]. Applied Mathematics and Mechanics, 2006, 27(4): 477－483. (in Chinese with English abstract)

[11] Spalart P. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2008, 41(41): 203－229.

[12] Shur M, Strelets M, Zajkov L, et al. Comparative numerical testing of one- and two-equation turbulence models for flows with separation and Reattachment[R]. Reno, NV: AIAA 1995－0863.

[13] Shur M, Spalart P, Strelets M, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29: 1638－1649.

[14] Strelets M. Detached eddy simulation of massively separated flows[R]. Reno, NV: AIAA 2001－0879.

[15] Menter F, Kuntz M. Development and application of a zonal DES turbulence model for CFX-5[R]. CFX-VAL17/0703, 2003.

[16] 胡偶，趙寧，沈志偉. SST-DDES模型在大分離流動(dòng)問(wèn)題中的應(yīng)用[J].南京航空航天大學(xué)學(xué)報(bào)，2017，49(2)：206－211. Hu Ou, Zhao Ning, Shen Zhiwei. Simulation of large separated flow with SST-DDES model[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49(2): 206－211. (in Chinese with English abstract)

[17] 劉周，楊云軍，周偉江，等. 基于RANS-LES混合方法的翼型大迎角非定常分離流動(dòng)研究[J]. 航空學(xué)報(bào)，2014，35(2)：372－380. Liu Zhou, Yang Yunjun, Zhou Weijiang, et al. Study of unsteady separation flow around airfoil at high angle of attack using hybrid RANS-LES method[J]. Acta Aeronautica ET Astronautica Sinica, 2014, 35(2): 372－380. (in Chinese with English abstract)

[18] 劉健，蔣永，吳金華. 基于iDDES的雙三角翼大迎角非定常渦破裂特征分析[J]. 工程力學(xué)，2016，33(4)：241－249. Liu Jian, Jiang Yun, Wu Jinhua. Analysis on characteristics of unsteady vortex breakdown flows around a double-delta wings at high incidence based on iddes method[J]. Engineering Mechanics, 2016, 33(4): 241－249. (in Chinese with English abstract)

[19] 趙偉文，萬(wàn)德成. 用DES分離渦方法數(shù)值模擬串列雙圓柱繞流問(wèn)題[J]. 應(yīng)用數(shù)學(xué)和力學(xué)，2016，37(12)：1272－1281. Zhao Weiwen, Wan Decheng. Detached-Eddy Simulation of flow past tandem cylinders[J]. Applied Mathematics and Mechanics, 2016, 37(12): 1272－1281. (in Chinese with English abstract)

[20] 夏明，張曉東，鐘伯文. 基于延遲脫體渦模擬方法對(duì)Gurney襟翼分離流動(dòng)的數(shù)值模擬[J]. 航空制造技術(shù)，2014，460(16)：114－117. Xia Ming, Zhang Xiaodong, Zhong Bowen. Numerical simulation of separated flow over gurney flap based on DDES[J]. Aeronautical Manufacturing Technology, 2014, 460(16): 114－117. (in Chinese with English abstract)

[21] 白俊強(qiáng)，王波，孫智偉. 使用RANS/LES混合方法對(duì)鈍前緣三角翼進(jìn)行數(shù)值模擬[J]. 空氣動(dòng)力學(xué)學(xué)報(bào)，2012，30(3)：373－379. Bai Junqiang, Wang Bo, Sun Zhiwei. The application of numerical simulation of delta wing with blunt leading edge using RANS/LES hybrid method[J]. Acta Aerodynamica Sinica, 2012, 30(3): 373－379. (in Chinese with English abstract)

[22] 王翔宇，李棟. SST-DES在小分離流動(dòng)數(shù)值模擬中的改進(jìn)[J]. 北京航空航天大學(xué)學(xué)報(bào)，2014，40(9)：1245－1249. Wang Xiangyu, Li Dong. Improved SST-DES in numerical simulation of mild separation[J]. Journal of Beijing University of Aeronautics & Astronautics, 2014, 40(9): 1245－1249. (in Chinese with English abstract)

[23] 靳瑤，蔡晉生，廖飛. Re=3900的圓柱繞流湍流模擬對(duì)比研究[J]. 應(yīng)用數(shù)學(xué)和力學(xué)，2016，37(12)：1282－1295. Jin Yao, Cai Jinsheng, Liao Fei. Comparative numerical studies of flow past a cylinder at Reynolds number 3900[J]. Applied Mathematics and Mechanics, 2016, 37(12): 1282－1295. (in Chinese with English abstract)

[24] 劉若陽(yáng)，侯安平，單樹(shù)軍，等. 基于DDES方法的葉柵分離旋渦的非定常流動(dòng)數(shù)值研究[J]. 推進(jìn)技術(shù)，2017，38(1)：16－26. Liu Ruoyang, Hou Anping, Shan Shujun, et al. Unsteady numerical investigation on cascade separation vortex flow based on delayed detached-eddy simulation [J]. Journal of Propulsion Technology, 2017, 38(1): 16－26. (in Chinese with English abstract)

[25] 杜若凡，閻超，韓政，等. DDES延遲函數(shù)在超聲速底部流動(dòng)中的性能分析[J]. 北京航空航天大學(xué)學(xué)報(bào)，2017，43(8)：1585－1593. Du Ruofan, Yan Chao, Han Zheng, et al. Performance of delayed functions in DDES for supersonic base flow[J]. Journal of Beijing University of Aeronautics & Astronautics, 2017, 43(8): 1585－1593. (in Chinese with English abstract)

[26] 唐雨萌，柳陽(yáng)威，陸利蓬. 高升力翼型復(fù)雜流動(dòng)模擬中湍流模型性能評(píng)估[J]. 航空動(dòng)力學(xué)報(bào)，2016，31(12)：2859－2869. Tang Yumeng, Liu Yangwei, Lu Lipeng, et al. Evaluation on turbulence models in simulating complex flows around high-lift airfoil[J]. Journal of Aerospace Power, 2016, 31(12): 2859－2869. (in Chinese with English abstract)

[27] Somers D M. Design and experimental results for the S809 airfoil[J]. Office of Scientific & Technical Information Technical Reports, 1997, 25(3): 555－562.

[28] 顧兆林. 風(fēng)揚(yáng)粉塵[M]. 北京：科學(xué)出版社，2010.

[29] 文曉慶，柳陽(yáng)威，方樂(lè)，等. 提高k-ω SST模型對(duì)翼型失速特性的模擬能力[J]. 北京航空航天大學(xué)學(xué)報(bào)，2013，39(8)：1127－1132. Wen Xiaoqing, Liu Yangwei, Fang Le, et al. Improving the capability of k-ω SST turbulence model for predicting stall characteristics of airfoil[J]. Journal of Beijing University of Aeronautics & Astronautics, 2013, 39(8): 1127－1132. (in Chinese with English abstract)

[30] 鐘偉，王同光. 湍流模型封閉常數(shù)對(duì)S系列翼型CFD模擬的影響[J]. 太陽(yáng)能學(xué)報(bào)，2013，34(10)：1690－1696. Zhong Wei, Wang Tongguang. Influence of closure coefficient of turbulence model on CFD simulations of S series airfoils[J]. Acta Energiae Solaris Sinica, 2013, 34(10): 1690－1696. (in Chinese with English abstract)

[31] Hand M M, Simms D A, Fingersh L J, et al. Unsteady aerodynamics experiment phase VI: Wind tunnel test configurations and available data campaigns[R]. Colorado: National Renewable Energy Laboratory, 2001.

[32] Li D S, Zhao Z X, Li Y R, et al. Effects of the particle Stokes number on wind turbine airfoil erosion[J]. Applied Mathematics and Mechanics: English Edition, 2018, 39(5): 639－652.

[33] 吳雙群，趙丹平. 風(fēng)力機(jī)空氣動(dòng)力學(xué)[M]. 北京：北京大學(xué)出版社，2011.

[34] 袁竹林. 氣固兩相流動(dòng)與數(shù)值模擬[M]. 南京：東南大學(xué)出版社，2013.

Effect of wind sand on flow around airfoil of wind turbine and its aerodynamic performance

Li Rennian1,2,3, Zhao Zhenxi1, Li Deshun1,2,3, Li Yinran1,2,3, Chen Xia1, Yu Jiaxin1

(1.,,730050,; 2.,730050,; 3.,730050,)

As a kind of clean and environment-friendly energy, wind power has been developed rapidly in recent years. With top wind power capacity, Northwest region is also a region with frequent dust storm incidents. Obviously, when wind turbine works under sand-wind conditions, its aerodynamics performance will be affected severely, and the flow structure around airfoil will be affected by the function of particles in the air. Wind turbine blades will even be eroded due to the impact of particles. Therefore, it is urgent to study the effect of sand-wind flow on wind turbine. The effect of particles on the flow structure around airfoil and its aerodynamic performance has been studied in this paper. In order to capture the detail of the flow structure around airfoil in various dusty environments with different particle diameters, a delayed detached eddy simulation (DDES) method, which is a hybrid Reynolds average Navier-Stokes equation and large eddy simulation (RANS-LES), and the discrete phase model were used for the simulation of the flow around NREL S809 airfoil. The flow structure around airfoil, mass distribution of particles and its aerodynamic performance in each dusty environment were compared. Both aerodynamic performance and flow structure were affected by particle, and the influences would be different when the angle of attack or particle diameter was different. When the angle of attack was small (6.1°, there was no flow detachment), the particles did not affect the flow around airfoil obviously, but the lift coefficient was decreased. With the increasing of particle diameter, lift coefficient of S809 decreased first and then went up, and turning point was 20m (3.9% lower than the lift coefficient obtained in clear air). Butthe lift coefficient could not be completely recovered, and it was still smaller than the lift coefficient in clear air when the particle diameter was 150m. When the angle of attack became larger (8.2°, flow detachment occurred), particles had a great influence on the flow structure around airfoil, such as the advancing of the flow separation point and the appearing of the flow along spanwise direction, and these influences were also affected by particle diameter. With particle diameter increasing, the flow structure became chaotic first and then gradually recovered. When the particle diameter was 20m, particles had the most effects on the aerodynamics performance of airfoil and the flow around it. This was due to the dramatic momentum exchange between particle and gas, that was, a large number of particles were rolled into wake area and broke the flow structure around airfoil, which affected the lift coefficient greatly. When the particle diameter was smaller than 20m, the particles would flow closely with air due to its weak inertia force. On the contrary, the particles would move independently of air flow, because of its strong inertia force when the particle diameter was larger than 50m. The flow structure recovered gradually with the increasing of particle diameter when particles diameter was larger than 20m. However, the aerodynamic performance of airfoil could not recover completely, only close to the lift coefficient in clear air, and the minimum value of lift coefficient was also obtained when the particle diameter was 20m (7.9% lower than thelift coefficient in clear air). In summary, the particles in the air will have a great influence on both the flow around airfoil and the aerodynamic performance of airfoil, especially in the area where the flow separates. When the particle diameter is smaller than 20m, the particle diameter increase will strengthen the effect, which reaches the climax when the particle diameter is 20m. Under this condition, if there is no flow detachment in clear air (the attack angle is small), the influence of particles would be weak, which can be ignored. If there exists flow separation phenomenon in clear air (the attack angle is large), then the influence would be strong, and it would aggravate the flow separation, causing the flow to transform into three-dimensional flow. After that, further increase of the particle diameter would weaken the effects of the particles, and when the particle diameter is 150m, both the flow structure and the lift coefficient are very close to that in clear air.

wind turbines; wind energy; computer simulation; delayed eddy simulation; airfoil; particle diameter; flow around airfoil; flow separation

10.11975/j.issn.1002-6819.2018.14.026

TK83

A

1002-6819(2018)-14-0205-07

2018-01-05

2018-05-20

國(guó)家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃（973計(jì)劃）（2014CB046201）；國(guó)家自然科學(xué)基金（51766009，51566011）

李仁年，教授，博導(dǎo)，主要從事流體機(jī)械理論及工程技術(shù)的研究。Email：lrn@lut.cn

李仁年，趙振希，李德順，李銀然，陳 霞，于佳鑫. 風(fēng)沙對(duì)風(fēng)力機(jī)翼型繞流及其氣動(dòng)性能的影響[J]. 農(nóng)業(yè)工程學(xué)報(bào)，2018，34(14)：205－211. doi：10.11975/j.issn.1002-6819.2018.14.026 http://www.tcsae.org

Li Rennian, Zhao Zhenxi, Li Deshun, Li Yinran, Chen Xia, Yu Jiaxin. Effect of wind sand on flow around airfoil of wind turbine and its aerodynamic performance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(14): 205－211. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.14.026 http://www.tcsae.org