冰蓋下梯形及拋物線形輸水明渠正常水深顯式迭代算法

韓延成，初萍萍，梁夢媛，唐 偉，高學平

?

冰蓋下梯形及拋物線形輸水明渠正常水深顯式迭代算法

韓延成1，初萍萍1，梁夢媛1，唐 偉1，高學平2

（1. 濟南大學資源與環境學院，濟南 250022；2. 天津大學水利工程仿真與安全國家重點實驗室，天津 300072）

隨著冬季用水量的增加，越來越多的輸水工程在冬季冰蓋下輸水，冰蓋下輸水已經成為一種常態化輸水方式，但目前對明渠正常水深的顯式計算方法的研究主要針對不結冰渠道的，缺少對冰蓋下輸水時正常水深的顯式計算方面的研究。該文推導了梯形斷面冰蓋下輸水時正常水深和流量關系，提出了正常水深的簡易顯式迭代算法，并經過證明，此迭代算法是收斂的。用同樣的方法，推導了拋物線形斷面冰蓋下輸水時正常水深和流量關系，提出了計算正常水深的簡易顯式迭代算法。算例表明，該文提出的冰蓋下梯形斷面和拋物線形斷面的顯式迭代算法具有形式簡單、計算量小、精度高，收斂性好的特點，一般需要3~5次迭代就可使誤差小于0.01 m，當增大迭代次數時，誤差進一步減小。研究為冰蓋下輸水渠道正常水深計算提供了便捷的計算方法，對冰期輸水渠道的設計及運行管理具有理論和實踐意義。

渠道；水力學; 設計; 明渠; 冰蓋下輸水；正常水深；顯式迭代算法

0 引 言

中國北方受蒙古高壓寒冷氣流的控制，冬季寒冷，北方10月以后大部分地區氣溫都會降到0℃以下，水體表面會發生結冰現象。隨著冬季反季節農業種植規模的擴大以及城市的發展，冬季需水量大幅增加。越來越多的工程采用常年輸水或冬季輸水。例如引黃濟青工程為冬季輸水渠道，輸水期為10月至翌年3月。南水北調東線山東段輸水期為10月至翌年5月。另外南水北調中線、引灤入津、引黃濟津、萬家寨引黃調水、新疆烏什水水庫引水工程等在結冰后也采用冰蓋下輸水的模式。除此之外，東北、西北、華北等地許多引水發電工程也采用冰蓋下輸水。冬季冰蓋下輸水已經成為一種重要的渠道輸水方式[1-2]。

正常水深的計算是渠道水力學計算的重要內容之一，在渠道設計、運行管理、輸水調度過程中大量使用[3]。但是正常水深與流量之間為復雜的非線性函數關系，不能直接求解，不方便工程應用[4-6]。學者們對正常水深的顯式求解方法進行了大量的研究，趙延風等[4,7]提出了梯形斷面的迭代算法，Bijankhan等[8]給出了蛋形斷面正常水深的迭代算法，Liu等[9]研究了馬蹄形斷面的正常水深的迭代算法，Li等[10]提出了拋物線形斷面正常水深的迭代算法。張新燕等[11]研究了拋物線形斷面的正常水深計算公式，張寬地等[12]研究了圓形隧洞正常水深的牛頓迭代算法，張新燕等[13-14]采用SAS軟件研究了U形渠道和圓形隧洞無壓流正常水深直接求解公式，武周虎[15]提出了蛋形斷面明渠正常水深的簡化算法。

這些顯式或直接計算方法，極大地方便了渠道設計者和運行管理者。但是已有的正常水深計算方法和公式是針對不結冰渠道的，對冰期輸水渠道，冰蓋的形成導致過流能力下降[16]，其正常水深計算需要考慮冰蓋阻力的影響；因此那些不結冰條件下正常水深的顯式計算公式是不適應的。目前還缺少對冰蓋下輸水時正常水深的顯式計算方法研究，對冰蓋下輸水渠道的運行和管理帶來了不便，研究冰蓋下正常水深的計算對冰期輸水渠道設計、運行具有重要意義。本文以梯形斷面、拋物線形斷面為研究對象，推導冰蓋下輸水時正常水深和流量之間的關系，提出梯形斷面、拋物線形斷面正常水深的簡易顯式迭代算法，對方便冰期輸水渠道在運行、設計中正常水深的計算具有現實意義。

1 梯形斷面冰蓋下輸水均勻流計算

由于冰蓋密度較水小，且柔性較大，冰蓋一般浮在水面。冰蓋下均勻流一般用曼寧公式表示為[17]

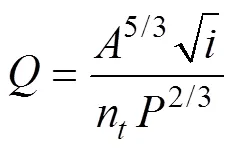
將式（2）代入式（1）得到冰蓋下輸水正常水深計算公式為

2 梯形斷面的正常水深的顯式迭代法

2.1 顯式迭代算法

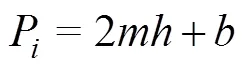
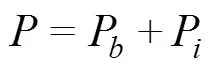
注：為水深，m；為底寬，m；為邊坡系數；下同。

Note:is water depth, m;is bottom width, m;is side slope; Same as below.

圖1 冰蓋下梯形渠道斷面示意圖

Fig.1 Schematic of cross section of trapezoid channel under ice cover

由式（9）可以看出，冰蓋下輸水糙率不是常數[2]，其與水深有關。將式（4）、（8）、（9）代入式（1），得到冰蓋下均勻流輸水流量的計算公式為

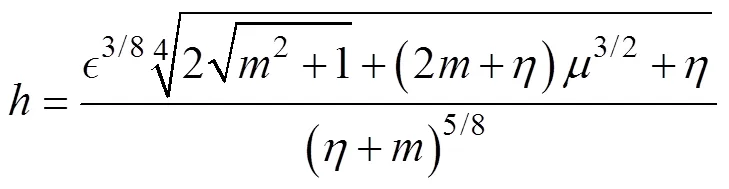
因此迭代公式可表示為

2.2 梯形斷面簡易迭代公式的應用

編制數值求解程序，采用埃特金迭代法或擬牛頓法[23]，求解式（10），得到正常水深h=3.745 138 7 m。將其作為理論參考值。

為了檢驗迭代公式的收斂性，采用不同初值0=0.01、0.1、1.0、2.0、5.294 2、10、100 m（其中，=5.294 2 m為根據水力最優斷面得到的正常水深），代入式（13）迭代得到結果如表1所示。可以看出，本迭代公式具有很好的收斂性，一般需要3～5次就可使誤差小于0.01 m。取水力最優斷面為初值時，只需要3次可使誤差小于0.01 m。除了上述初值，也用其他初值經過檢驗，不論初值多少，公式均具有良好的收斂效果。當增大迭代次數時，不論初值為多少，均能收斂于理論值。

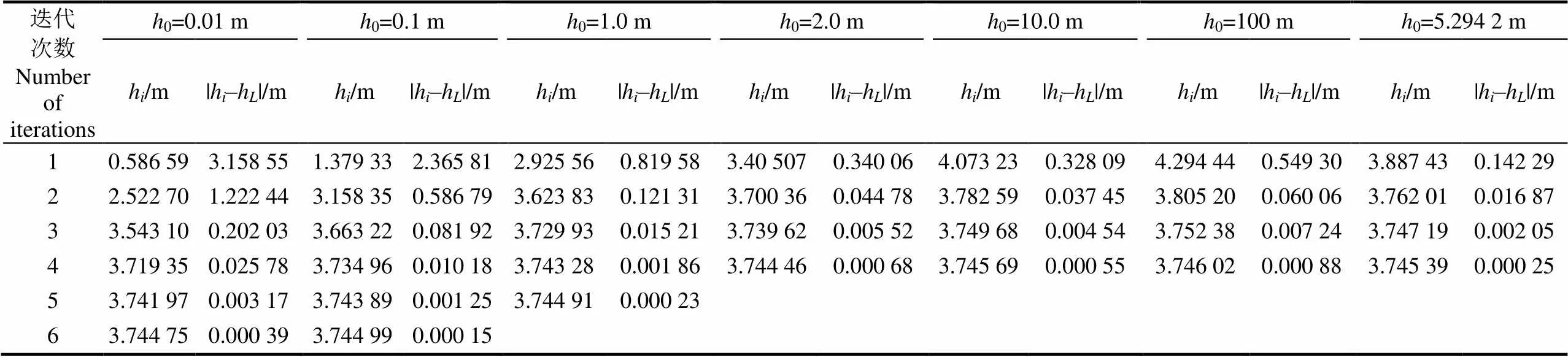
表1 梯形斷面不同初值時正常水深的迭代結果

注：0為初始值，h為第次迭代結果，h理論參考值。下同。

Note:0is the initial value;his the value of thethiteration for normal depth,his the theoretical value of normal depth. Same as below.

3 冰蓋下拋物線形斷面的正常水深顯式迭代算法

3.1 冰蓋下拋物線形渠道均勻流計算

學者們普遍認為拋物線形斷面（見圖2）具有拐點少、應力集中點少、裂縫少、滲漏小，另外具有穩定性好、過流能力大，水力學特性優良的特點[24-27]。巴基斯坦的High Level渠，西班牙Genil-Cabra渠等采用了拋物線形斷面[28]。

拋物線形斷面形狀可表示為[17,29-31]

注：為水面寬度；為水深，m。

Note:is width of water surface, m;is water depth, m.

圖2 冰蓋下拋物線形渠道斷面特性

Fig.2 Cross section characteristics of parabolic channel under ice cover

濕周包括渠床濕周和冰蓋造成的濕周，分別表示為

將式（22）代入式（2），可以得到綜合糙率為

將式（21）～式（23）代入曼寧公式（1），簡化后得到流量和水深的關系式為

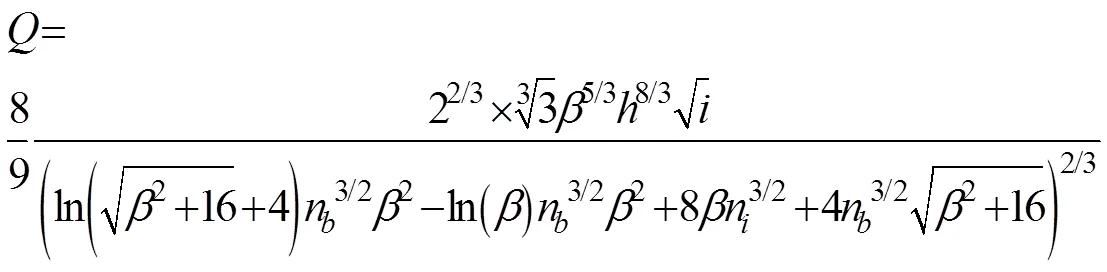
3.2 顯式迭代法公式構建

根據式（25），構造的迭代公式為

為了減小迭代次數，初值可取非冰蓋下拋物線形最優斷面得到的水深[26-27]

用同樣的方法，可以證明式（26）是收斂的，在此不在贅述。

3.3 顯式迭代法公式應用

編制數值求解程序，采用埃特金迭代法或擬牛頓 法[23]，均可得到正常水深h=3.846 841 14 m。將其作為理論參考值。

根據水力最優斷面公式（27），得到水力最優斷面條件下0=3.040 4 m。取不同初值（0=0.01、0.1、1.0、5.0、10.0、100、3.040 4 m），根據迭代公式（26）得到結果如表2所示。

可以看出，本迭代公式具有很快的收斂速度，一般需要3~5次就可使誤差小于0.01 m。取最優斷面為初值時，只需要3次可使誤差小于0.01 m。當增大迭代次數時，不同初值，均能收斂于理論值。

表2 拋物線形斷面不同初值正常水深迭代結果

4 結 論

本文推導了冰蓋下輸水時梯形斷面和拋物線形斷面綜合糙率及流量計算公式，根據理論推導提出了冰蓋下梯形斷面和拋物線形斷面正常水深顯式迭代算法，得到如下結論：

1）提出了冰蓋下梯形斷面和拋物線形斷面的新的迭代公式，具有形式簡單，計算方便的特點，采用不同初值，均能收斂于理論值。

2）通過理論證明，本文提出的冰蓋下梯形斷面和拋物線形斷面正常水深的迭代公式是收斂的。

3）實例表明，本文提出的迭代公式具有很好的收斂性，一般需要3～5次就可使誤差小于0.01 m。增加迭代次數后都能收斂到理論值。

[1] 穆祥鵬，陳文學，郭曉晨，等. 高緯度地區渠道無冰蓋輸水的冰情控制研究[J]. 水利學報，2013，44(9)：1071－1079. Mu Xiangpeng, Chen Wenxue, Guo Xiaochen et al. Study on long-distance water transfer channel with thermal insulation cover in winter[J]. Journal of Hydraulic Engineering, 2013, 44(9): 1071－1079. (in Chinese with English abstract)

[2] Han Yancheng, Xu Zhenghe, Easa S M, et al. Optimal hydraulic section of ice-covered open trapezoidal channel[J]. Journal of Cold Regions Engineering, 2017, 31 (3): 06017001. DOI: 10.1061/(ASCE)CR.1943-5495.0000128

[3] 韓延成，徐征和，高學平，等. 二分之五次方拋物線形明渠設計及提高水力特性效果[J]. 農業工程學報，2017，33(4)：131－136. Han Yancheng, Xu Zhenghe, Gao Xueping, et al. Design of two and a half parabola-shaped canal and its effect in improving hydraulic property[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(4): 131－136. (in Chinese with English abstract)

[4] 趙延風，祝晗英，王正中，等. 梯形明渠正常水深的直接計算方法[J]. 西北農林科技大學學報：自然科學版，2009，37(4)：220－224. Zhao Yanfeng, Zhu Hanying, Wang ZhengZhong, et al. A direct formula for normal depth in trapezoidal open channel[J]. Journal of Northwest A &F University: Nat Sci Ed, 2009, 37(4): 220－224. (in Chinese with English abstract)

[5] 張寬地，呂宏興，趙延風. 明流條件下圓形隧洞正常水深與臨界水深的直接計算[J]. 農業工程學報，2009，25(3)：1－5.Zhang Kuandi, Lü Hongxing, Zhao Yanfeng. Direct calculation for normal depth and critical depth of circular section tunnel under free flow[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(3): 1－5. (in Chinese with English abstract)

[6] 張新燕，呂宏興. 拋物線形斷面渠道正常水深的顯式計算[J]. 農業工程學報，2012，28(21)：121－125. Zhang Xinyan, Lü Hongxing. Explicit solution for normal depth in parabolic-shape channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(21): 121－125. (in Chinese with English abstracts)

[7] 王正中，席跟戰，宋松柏，等. 梯形明渠正常水深直接計算公式[J]. 長江科學院院報，1998，15(6)：1－7. Wang Zhengzhong, Xi Genzhan, Song Songbai, et al. A direct calculation formula for normal depth in open trapezoidal channel[J]. Journal of Yangtze River Scientific Research Institute, 1998, 15(6): 1－7. (in Chinese with English abstract)

[8] Bijankhan M and Kouchakzadeh S. Egg-shaped cross

section: Uniform flow direct solution and stability identification[J]. Flow Measurement and Instrumentation, 2011, 22(6), 511－516.

[9] Liu Jiliang, Wang Zhengzhong, and Fang Xing. Iterative formulas and estimation formulas for computing normal depth of horseshoe cross-section tunnel[J]. Journal of Irrigation and Drainage Engineering, 2010, 36(11): 786－790.

[10] Li Yonghong, Gao Zhaoliang. Explicit solution for normal depth of parabolic section of open channels[J]. Flow Measurement and Instrumentation, 2014, 38: 36－39.

[11] 張新燕，呂宏興. 拋物線形斷面渠道正常水深的顯式計算[J]. 農業工程學報，2012，28(21)：121－125. Zhang Xinyan, Lü Hongxing. Explicit solution for normal depth in parabolic-shape channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(21): 121－125. (in Chinese with English abstracts)

[12] 張寬地，呂宏興，趙延風. 明流條件下圓形隧洞正常水深與臨界水深的直接計算[J]. 農業工程學報，2009，25(3)：1－5.Zhang Kuandi, Lü Hongxing, Zhao Yanfeng. Direct calculation for normal depth and critical depth of circular section tunnel under free flow[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(3): 1－5. (in Chinese with English abstract)

[13] 張新燕，呂宏興，朱德蘭. U形渠道正常水深的直接水力計算公式[J]. 農業工程學報，2013，29(14)：115－119. Zhang Xinyan, Lü Hongxing, Zhu Delan. Direct calculation formula for normal depth of U-shaped channel[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(14): 115－119. (in Chinese with English abstract)

[14] 張新燕，呂宏興. 無壓圓形隧洞正常水深直接算法[J]. 水力發電學報，2014，33(1)：127－131. Zhang Xinyan, Lü Hongxing. Direct calculation method for normal depth in non-pressure circular tunnel[J]. Journal of Hydroelectric Engineering, 2014, 33(1): 127－131. (in Chinese with English abstract)

[15] 武周虎.蛋形斷面明渠正常水深和臨界水深的簡化算法[J]. 人民長江，2014(4)：73－76.Wu Zhouhu. Simplified algorithm of normal depth and critical depth of egg-shape cross-section open channel[J]. Yangtze River, 2014(4): 73－76. (in Chinese with English abstract)

[16] 楊開林. 明渠冰蓋下流動的綜合糙率[J]. 水利學報，2014，45(11)：1310－1317. Yang Kailin. Composite roughness of ice-covered flows in open channels[J]. Journal of Hydraulic Engineering, 2014, 45(11): 1310－1317. (in Chinese with English abstract)

[17] Chow V T. Open Channel Hydraulics[M]. New York: McGraw-Hill, 1959.

[18] Uzuner M S. The composite roughness of ice covered streams[J]. Journal of Hydraulic Research, 1975, 13(1): 79－102.

[19] 顏丙池. 南水北調冰期輸水原型觀測與研究[J]. 河北水利水電技術，2002(2)：41－42. Yan Bingchi. Prototype observation and research for South- to-North Water Diversion Project during freezing period[J]. Water Conservancy and Hydropower Technology of Hebei, 2002(2): 41－42. (in Chinese with English abstract)

[20] 馬喜祥，白世錄，袁學安，等. 中國河流冰情[M]. 鄭州：黃河水利出版社，2009

[21] 穆祥鵬，陳文學，崔巍，等. 南水北調中線干渠冰期輸水能力研究[J]. 南水北調與水利科技，2009，7(6)：118－122. Mu Xiangpeng, Chen Wenxue, Cui Wei et al. Study on water diversion capacity in the middle route of the south- to-north water transfer project in ice period[J], South- to-North Water Transfers and Water Science & Technology, 2009, 7(6): 118－122. (in Chinese with English abstract)

[22] 顏慶津. 數值分析[M]. 北京：北京航天航空大學出版社，2006.

[23] 周長發. 科學與工程數值算法：Visual Basic 版[M]. 北京：清華大學出版社，2002.

[24] Mironenko A P, Willardson L S, Jenab S A. Parabolic canal

design and analysis[J]. Journal of Irrigation and Drainage Engineering, 1984, 110(2): 241－246.

[25] Han Yancheng. Horizontal bottomed semi-cubic parabolic channel and best hydraulic section[J]. Flow Measurement and Instrumentation, 2015, 45: 56－61.

[26] Han Yancheng, Easa S M. Superior cubic channel section and analytical solution of best hydraulic properties[J]. Flow Measurement and Instrumentation, 2016, 50: 169－177.

[27] Han Yancheng, Easa S M. New and improved three and one-third parabolic channel and most efficient hydraulic section[J]. Canadian Journal of Civil Engineering, 2017, 44(5): 387－391.

[28] Anwar A A, de Vries T T. Hydraulically efficient power-law channels[J]. Journal of Irrigation and Drainage Engineering, 2003, 129(1): 18－26.

[29] Hu Han, Huang Jiesheng, Qian Zhongdong, et al. Hydraulic analysis of parabolic flume for flow measurement[J]. Flow Measurement and Instrumentation, 2014, 37: 54－64.

[30] Han Yancheng, Gao Xueping., Xu Zhenghe. The best hydraulic section of horizontal-bottomed parabolic channel section[J]. Journal of Hydrodynamics, 2017, 29(2): 305－313.

[31] Loganathan G V. Optimal design of parabolic canals[J]. Journal of Irrigation and Drainage Engineering, 1991, 117(5): 716－735.

Explicit iterative algorithm of normal water depth for trapezoid and parabolic open channels under ice cover

Han Yancheng1, Chu Pingping1, Liang Mengyuan1, Tang Wei1, Gao Xueping2

(1.250022,; 2.300072,)

With the increase of water demand in winter in northern China, more and more open-channel water diversion projects transport water under the ice cover in winter such as the Middle Route of South-to-North Water Diversion Project. The method of transporting water using open channel under the ice cover has become increasingly common to delivery water from reservoirs, rivers and lakes to cities. The normal water depth is an important parameter in channel design, operation, flood control, and flow measurement and maintenance of the open channel or sewage systems. The explicit calculation algorithms of the normal water depth for the open channel are mainly for free-ice channels. This paper proposed algorithm of normal water depth of open channel under ice cover. The expression of the synthesis roughness for the flow of the channel under the ice cover was determined based on the studies of Sabaneev. The relationship between the normal water depth and the flow rate of the trapezoid section under the ice cover was derived. A simple explicit iterative algorithm to compute the normal water depth was then proposed. It proved that the new iterative algorithm was convergent using the convergence theory of iteration. The formula to getting the initial value was proposed using the best hydraulic section. The application examples were given to compute the normal depth under the ice cover by using the new iterative algorithm. The results showed that the explicit iterative algorithm proposed had a fast convergence speed. In general, the error would be less than 0.01 m with only 3-5 times iterations. The number of the iteration decreased when using the initial value from the best hydraulic section. When the number of iterations was increased, the iterative value would be closer to the theoretical value of the normal depth. By using the same method, the relationship between the normal water depth and the flow rate under the ice cover was derived for the parabolic section, and a simple explicit iterative algorithm for calculating the normal depth of water was proposed too. The examples showed that the explicit iterative formula of the parabolic section proposed was simple and had a fast convergence speed too. In general, the error would be less than 0.01 m with only 3-5 times iterations as well as trapezoid section. The study of this paper provides a convenient method for the calculation of the normal water depth of the water conveyance channel under the ice cover. The research has theoretical and practical significance for the design, operation and management of the water conveyance channels under the ice cover because the normal depth is most widely used in the water conservancy project.

canals; hydraulic; design; open channel; water transport under ice cover; normal depth of water; explicit iterative algorithm

10.11975/j.issn.1002-6819.2018.14.013

TV 131.4

A

1002-6819(2018)-14-0101-06

2018-01-31

2018-05-10

國家“十二五”科技支撐計劃（2015BAB07B02-6）；山東省自然科學基金(ZR2017LEE028); 山東省重點研發計劃（2016GSF117038）

韓延成，甘肅武威人，副教授，主要從事水力學及河流動力學方面的研究。Email：stu_hanyc@ujn.edu.cn

韓延成，初萍萍，梁夢媛，唐 偉，高學平.冰蓋下梯形及拋物線形輸水明渠正常水深顯式迭代算法[J]. 農業工程學報，2018，34(14)：101－106. doi：10.11975/j.issn.1002-6819.2018.14.013 http://www.tcsae.org

Han Yancheng, Chu Pingping, Liang Mengyuan, Tang Wei, Gao Xueping. Explicit iterative algorithm of normal water depth for trapezoid and parabolic open channels under ice cover[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(14): 101－106. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.14.013 http://www.tcsae.org