空間多層次誤差移動平均模型的廣義矩估計
——基于廣東省產業知識溢出三維非平衡面板數據

葉倩婷，龍志和（博士生導師），吳 梅（副教授），陳青青（博士）

一、引言

經濟管理研究中的數據常呈現層級結構分布，數據層級間相互嵌套、相互作用，被稱為層級數據[1][2]；層級數據包含了經濟管理研究中常用的面板數據，對面板數據維度作了進一步延伸。常見的面板數據空間模型主要關注數據的空間特性，卻未考慮數據的層級結構以及層級間的嵌套關系。

為深入挖掘層級數據的內在規律，需要進一步拓展空間多層次計量經濟學模型，即同時考慮研究對象層級間的嵌套關系和層級數據的空間相關關系，以及多層次模型誤差項的空間相關性，建立并研究空間多層次滯后模型和空間多層次誤差模型及其衍生結構組合模型。現有文獻中，對空間多層次計量經濟學模型研究得并不多。Corrado和Fingleton[3]探索性地提出了空間多層次計量經濟學模型的結構，但未對其具體的參數估計方法做深入討論。在層級數據空間計量模型參數估計方面，Baltagi等[4]提出了空間多層次滯后（HSLAG）模型，并使用工具變量法（IV）以及兩階段最小二乘法（2SLS）對模型的參數進行估計；葉倩婷、龍志和[5]使用廣義矩（GMM）估計法和可行的廣義最小二乘法（FGLS），對空間多層次誤差自回歸（HSEAR）模型的參數進行了估計；隨后，Fingleton等[6]把HSEAR模型用于分析英格蘭房價的空間關系與層級嵌套關系。

然而，對于空間多層次誤差模型而言，HSEAR模型在考察層級效應的基礎上僅關注鄰接地區數據誤差的空間自相關關系，該如何同時考慮層級效應以及衡量地區自身所受到的空間誤差沖擊呢？這就需要對誤差項進行高階自回歸。當自回歸過程階數提高，為減少待估參數的數量，移動平均過程的存在顯得尤為必要。空間多層次誤差移動平均（HSEMA）模型該如何建立，其參數該如何估計，模型可以如何應用，均為本文需展開研究的內容。

模型建立方面，由于層級數據存在層級嵌套關系，本文將以空間誤差移動平均（SEMA）模型為基礎，將嵌套誤差項引入SEMA模型，構建HSEMA模型。模型參數估計方面，Fingleton、Le Gallo[7]推導了截面數據SEMA模型可行的廣義空間兩階段最小二乘（FGS2SLS）估計，并指出SEMA模型估計量的推導與SEAR模型有許多相似之處，但在其細節與意義上有很大的區別。本文參考Fingleton[8]對面板SEMA模型參數的GMM估計方法，對HSEMA模型參數進行估計。HSEMA模型可以同時衡量研究對象自身的誤差沖擊效應，并考慮數據層級結構，進而對其產生的空間誤差移動平均系數和層級效應進行有效測量，填補當空間多層次誤差模型的誤差項存在移動平均結構時，其估計方法的空白，以期推進空間多層次模型的理論研究。進一步，在模型應用方面，采用2005～2013年廣東省21個地級市所具有不同數量工業產業的“時間—地區—產業”三維非平衡面板數據，同時考慮數據中的層級嵌套效應與空間溢出作用，對產業間知識溢出效應進行實例分析。

二、空間多層次誤差移動平均（HSEMA）模型

空間多層次誤差移動平均（HSEMA）模型構建思路如下，參考前人對HSLAG和HSEAR模型的研究[4][5][9]，以測量時間—地區—產業（此層級亦可為省、市、縣）三維數據為例，建立HSEMA模型：

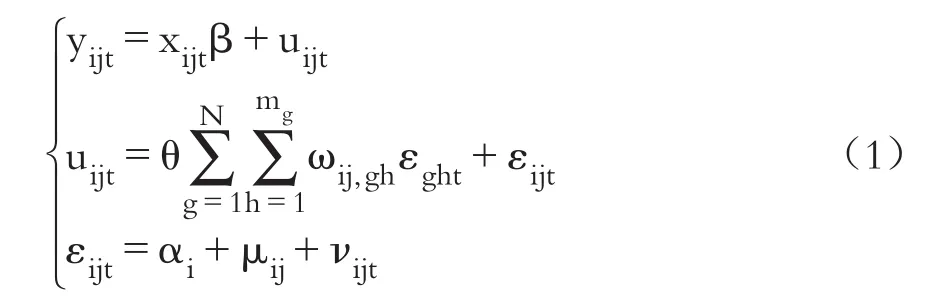
其中：i=1，…，N；j=1，…，mi；t=1，…，T；記yijt為t時期i地區j產業因變量的觀測值；xijt為一個1×K維觀測向量；β是一個K×1維參數向量；uijt為t時期i地區j產業的誤差項；εijt為t時期i地區j產業的由于未被考慮到的變量所引致的新息誤差，且具有誤差分量結構；θ是空間誤差移動平均系數，衡量在j點自身的誤差沖擊效應大小，它只影響在空間權重矩陣非零元素對應的產業間有直接相互作用的位置，這樣的沖擊效應為局部的空間相關性；兩個層級隨機效應誤差分量結構αi和μij分別代表地區隨機效應，以及第j個產業嵌套于第i個地區中的嵌套隨機效應；νijt為其他誤差沖擊因素。HSEMA模型設定與估計的前提假設與HSEAR模型類似。此外，這個模型允許每個地區的產業數量不相等，地區間可以有不同數量的觀測時期，即適用于非平衡面板數據。

模型（1）可轉換為矩陣形式：

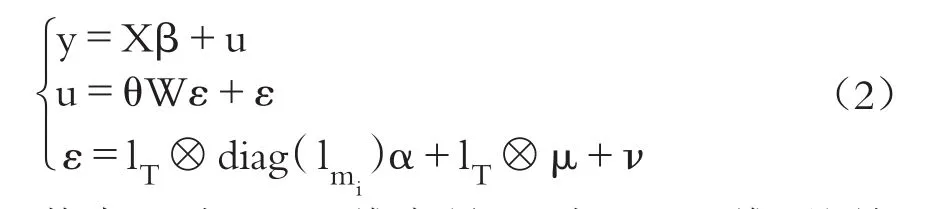
其中：y為TS×1維向量；X為TS×K維觀測矩陣，假設X為列滿秩且其元素絕對值一致有界；β的維度為K×1，u的維度為TS×1；αT=（α1，…，αN），μ是S×1維向量，ν與u類似定義；lT為T×1維全1列向量；W=IT?WS，?為克羅內克積，WS是一個已知的S×S維空間權重矩陣，且主對角線上元素為0，WS由 N2個子矩陣組成，WS=［Wig］，其中 i、g=1，…，N ，其子矩陣Wig的維數為mi×mg，即Wig=［ωij，gh］，其中j=1，…，mi，h=1，…，mg；ITS=IT?IS為TS×TS維單位矩陣，（ITS+θW）為TS×TS維非奇異矩陣，且|θ|＜1成立。

因為E［u］=0，誤差項u的方差協方差矩陣為：

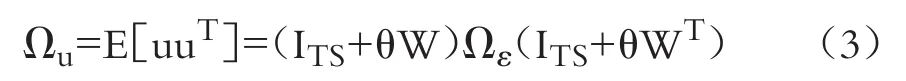
其中，由于ε的誤差分量結構與HSEAR模型的設定相同，故ε的方差協方差矩陣Ωε和與HSEAR模型一致。

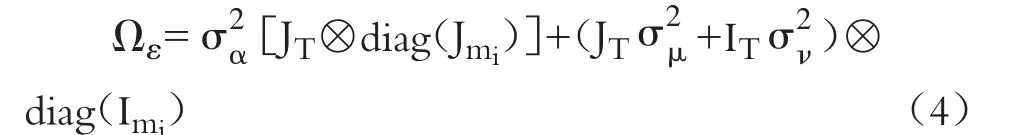
經譜分解后，方差協方差矩陣Ωε的逆可表達如下：

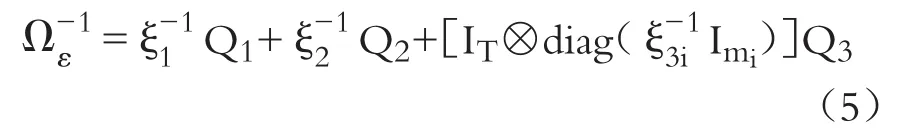
三、廣義矩（GMM）估計

本文借鑒Kapoor等[10]與Fingleton[8]的GMM估計研究框架，推導HSEMA模型的矩條件，據此定義其參數的最優權重GMM估計量。區別于HSEAR模型，推導HSEMA模型矩條件主要涉及、、。為了計數方便，令：

為了得到這些變量的期望，對2≤T≤∞求得18個矩條件，如表1所示。

那么由式（2）和（6）可得：

對?i=1，2，3，左乘Qi至式（7）有：

不難得到以下二次型：

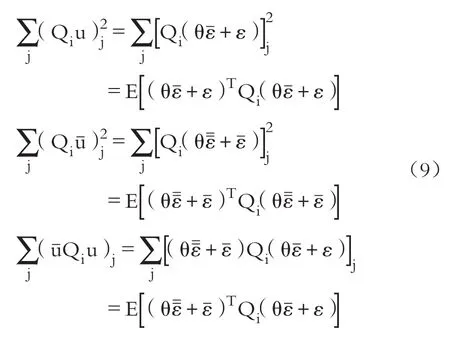
將矩條件代入式（9），記：

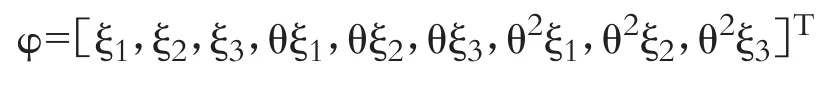
得到包含參數θ、ξ1、ξ2和ξ3的矩函數體系：

由辛欽（Wiener-khinchin）大數定理，只要樣本容量達到充分大，樣本矩收斂到總體矩的概率等于1。令為β的一致估計量，則：

令參數向量為ψ=（θ，ξ1，ξ2，ξ3），且ψ∈△，其中△=［-a，a］×［0，b］×［0，c］×［0，d］，a≥1，b≥bν，c≥式（11）對應關于和的樣本形式為：

這里?（ψ）是一個殘差向量。

顯然，式（10）中的前三個等式與ξ2和ξ3無關，后六個等式與ξ1無關 。令可改寫為：

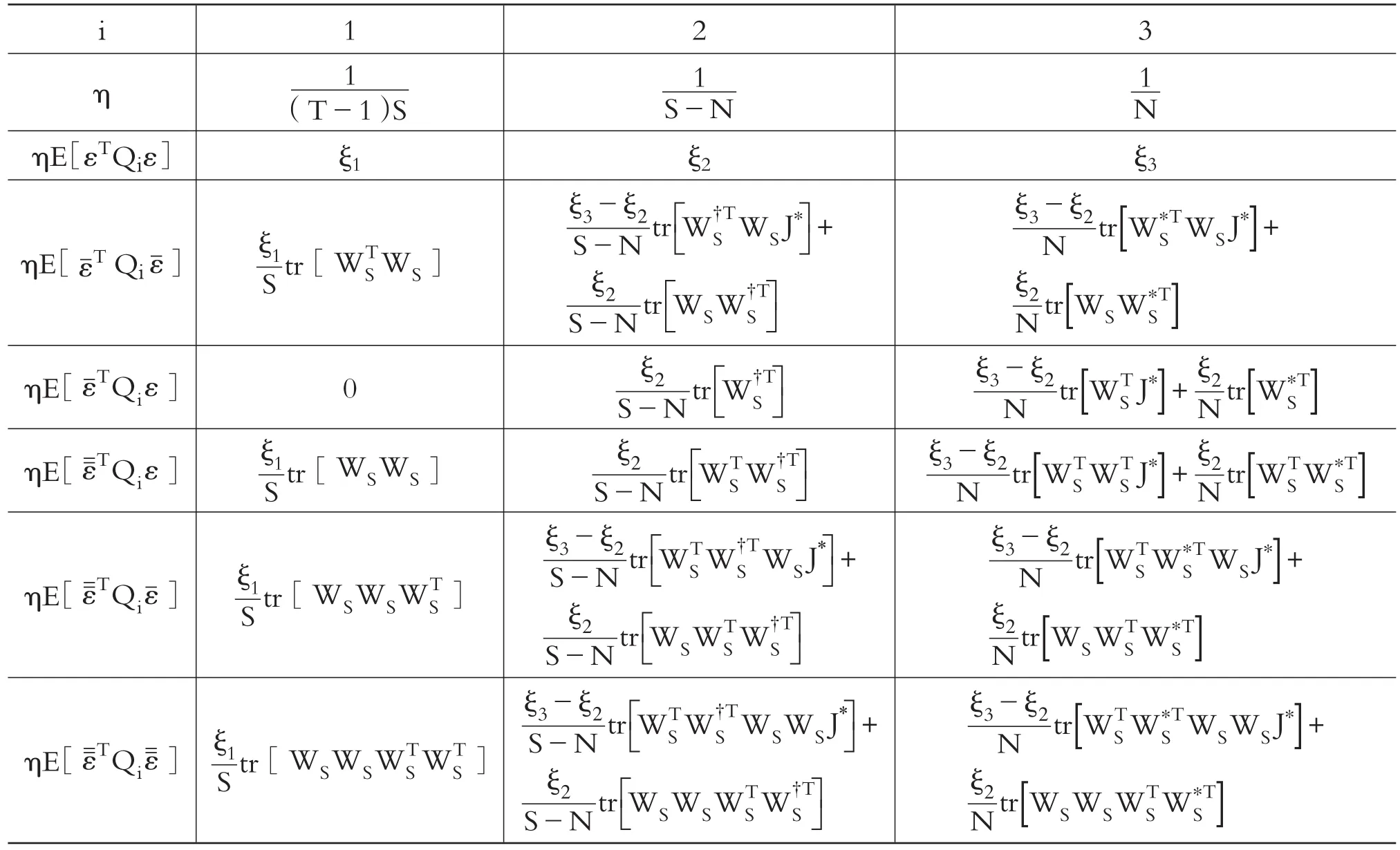
表1 HSEMA模型矩條件

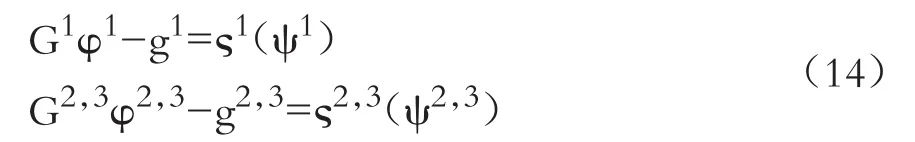
基于GMM估計的基本規范與論述[11][12]，采用矩條件的方差協方差矩陣構建最優權重矩陣，從而得到漸近有效的GMM估計量，將樣本矩之間的加權距離最小化。那么最優權重GMM估計量定義為：

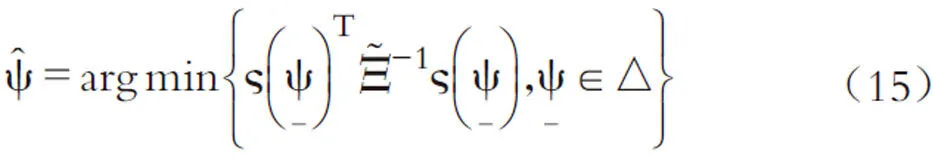
此處要求參數空間△為緊集，從而保證GMM估計量的一致性。

由于模型誤差項ε的方差協方差矩陣Ωε不是常數，式（2）中總體回歸系數β的廣義最小二乘（GLS）估計量為：

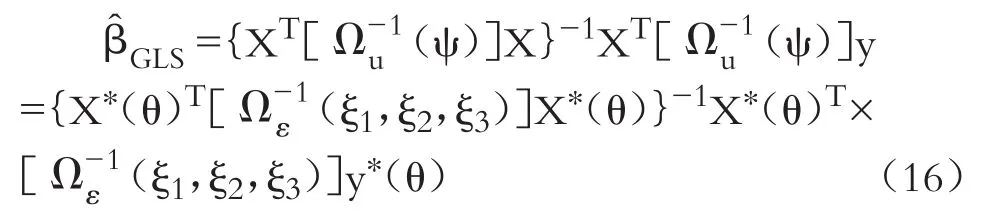
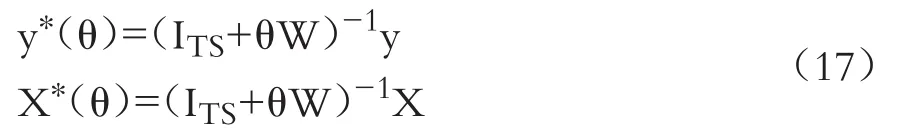
變量y?（θ）和X?（θ）可看成原始模型（2）的空間科克倫—奧克特變換。

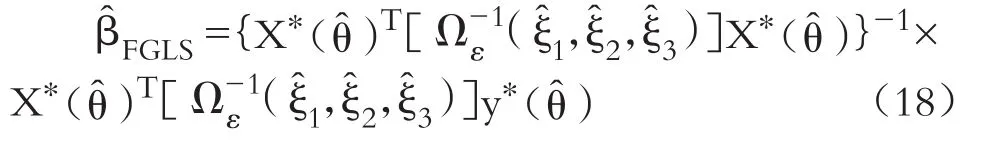
四、基于HSEMA模型的廣東省工業產業知識溢出實例分析

“粵港澳大灣區”已經上升到我國經濟發展的核心戰略地位。本文以三維非平衡層級數據為例，對廣東省工業產業知識溢出效應進行研究。由下圖可以看出廣東省技術密集型產業工業增加值占比均超過50%，且逐年遞增，說明廣東省工業產業結構以技術密集型為主導。弄清廣東省是否存在知識溢出效應且為何種知識溢出效應，對“粵港澳大灣區”經濟發展規劃意義重大。

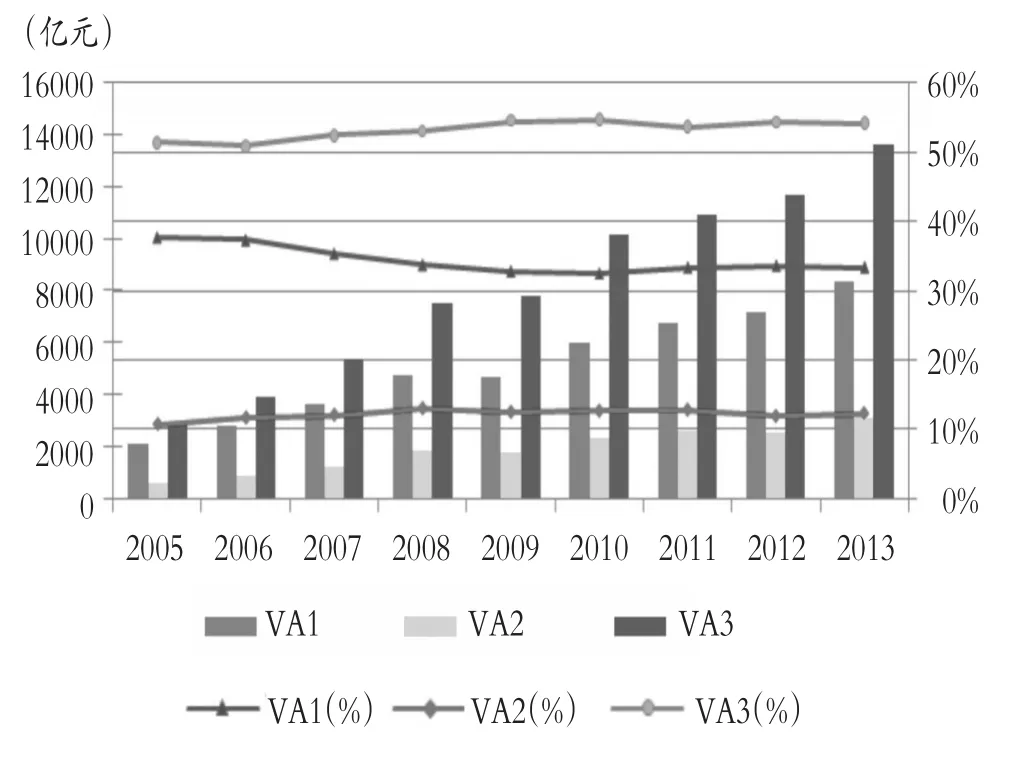
2005～2013年廣東省按資源密集度分類工業增加值圖

有關工業產業的知識溢出效應，國內外學者依據不同地區、不同時期的數據做了大量研究[13][14]，研究產業經濟增長是如何受知識溢出影響的[15]。然而，已有研究未同時考慮數據間存在的空間效應和層級結構，可能對知識溢出程度的估計產生偏差。廣東省經濟總量以及GDP增速等主要經濟指標均位居各省前列，對全國的經濟增長有重要的支撐和標桿作用。實際經濟管理數據經常為“多維度”“不完整”的非平衡數據，為了進一步考察工業產業的知識溢出效應對經濟的影響，采用HSEMA模型，使用廣東省9個年度、21個地級市所具有不同數量工業產業的三維非平衡面板數據進行實例分析。

本文所需數據取自2006～2014年《廣東統計年鑒》和《廣東工業統計年鑒》，所選取產業類別參考國家統計局2002年對工業產業的分類。

考慮數據的層級結構和空間效應，考察工業產業知識溢出效應對經濟增長的作用。此處采用Cobb-Douglas生產函數，令第“t年—i地區—j產業”的工業增加值為模型的因變量，技術水平、勞動力和物質資本投入為自變量：

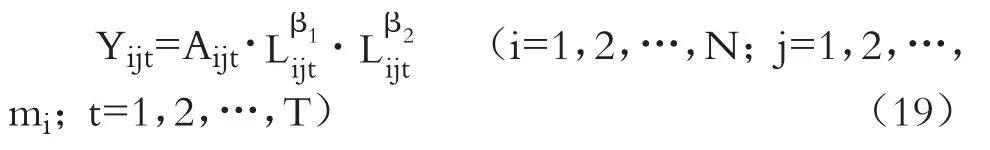
其中，i代表第i個地區，j表示第j個產業，t代表時間，采用頻度為年的數據。Y代表工業增加值，A代表技術水平，L為勞動力投入，K為物質資本投入。為便于估計和消除量綱影響，對方程（19）兩邊取對數，得到以下模型：

對方程（20）中的技術水平A進行分解，包括以下三個外溢指標：MAR外溢（某地區專注于某一類產業的專業化生產能促使該地區經濟增長）、Jacobs外溢（地理位置鄰近的地區產業多元化比產業結構單一更能促進產業創新和經濟增長）和Porter外溢（產業間的相互競爭、優勝劣汰促使產業知識更新換代推動經濟增長），分別代表產業專業化、多元化與競爭性外溢，用SPEC、DIV和COMP表示其變量名稱。由式（1）和式（20）得到基于空間多層次誤差移動平均模型的知識溢出效應實證分析基礎理論模型：

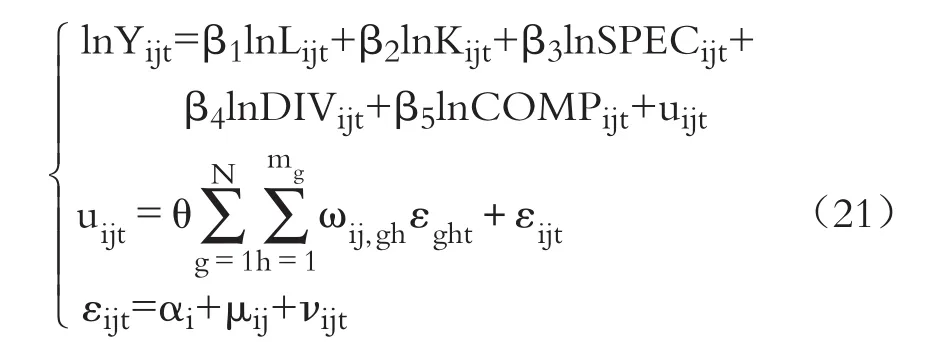
其中，Yijt為t年i地區j產業的工業增加值，衡量產業的發展；Lijt、Kijt、SPECijt、DIVijt、COMPijt為 t年i地區j產業影響產業發展的要素；μij為t年i地區j產業的誤差項。θ是空間誤差移動平均系數，誤差項εijt具有移動平均結構以及誤差成分結構，αi為地區隨機效應，μij為第j個產業嵌套于第i個地區中的嵌套隨機效應，νijt為其他誤差沖擊因素。各變量意義與對應參數如表2所示：

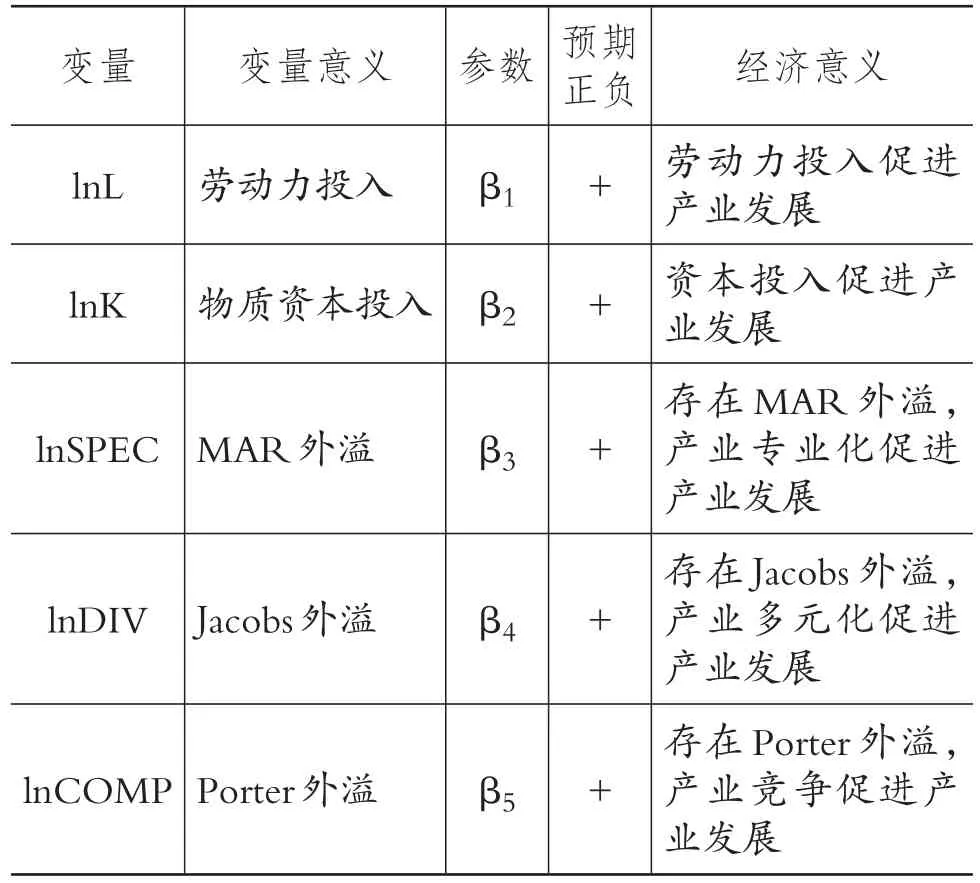
表2 指標體系設定與預期經濟意義

根據Batisse[16]和Mihn[17]的方法計算專業化指標（MAR 外溢）lnSPECijt，根據 Ellison、Glaeser[18]的方法計算多元化指標（Jacobs外溢）lnDIVijt，根據De Lucio等[19]的方法計算競爭性指標（Porter外溢）lnCOMPijt，以t年i地區j產業的工業增加值（或從業人數、企業個數）占全國該產業對應指標的比重，描述知識溢出效應（即份額相對值或比例相對值）。

使用上述2005～2013年廣東省“時間—地區—產業”的三維非平衡面板數據，采用混合回歸模型和面板數據SEMA模型，與HSEMA模型進行對比。對混合回歸模型，若該地區無對應產業，則以空值替代，其參數使用OLS估計；根據Fingleton[8]的估計方法對SEMA模型參數進行估計；對HSEMA模型，運用本文提出的最優權重GMM估計量對其誤差項標準差進行估計，進而對總體回歸參數進行FGLS估計。估計運算用GAUSS 15.0軟件進行編程，結果見表3。

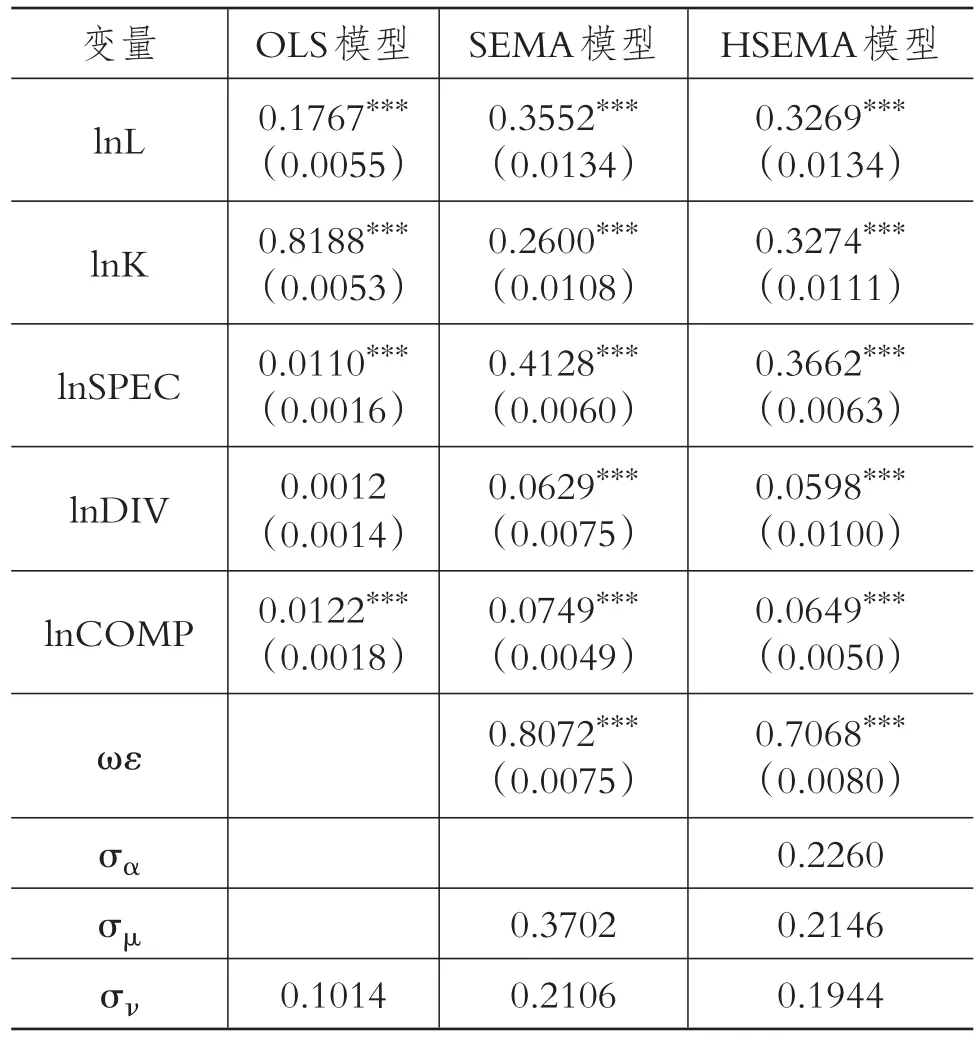
表3 空間多層次誤差移動平均模型參數估計

從實證結果可以看到，混合回歸模型中勞動力和物質資本投入，以及其他各知識溢出效應對工業增加值存在推動作用，OLS估計結果認為物質資本投入彈性（0.8188）的作用遠超出勞動力投入彈性（0.1767），即廣東工業產業發展主要依靠物質資本投入，與事實不符。變量lnDIV對應的參數不顯著，說明產業多元化結構對廣東省產業發展沒有顯著影響，其余各參數估計值均在1%的水平上顯著為正值，但產業專業化和競爭性溢出彈性估計值分別為0.0110和0.0122，即廣東省工業產業專業化程度與競爭對工業增加值影響甚微，此結果與廣東省的技術密集型特征明顯相悖。混合回歸模型單純地將9個年度廣東省所有地區的數據一起回歸，核心變量lnL和lnK的方差膨脹因子（VIF）均大于10，有較嚴重的多重共線性，而且忽略了數據的時間跨度、層級特性與空間溢出作用，造成過度擬合、最小二乘估計結果與現實背離，導致回歸結果失真。

從SEMA和HSEMA模型估計結果可知，模型考慮數據中的時間跨度與空間效應，其參數估計值都在1%的水平上顯著為正，勞動力投入彈性分別為0.3552和0.3269，物質資本投入彈性分別為0.2600和0.3274，MAR外溢彈性分別為0.4128和0.3662，Jacobs外溢彈性分別為0.0629和0.0598，Porter外溢彈性分別為0.0749和0.0649。這說明本文所列出的各項指標均對工業增加值具有促進作用，不同于混合回歸模型，產業專業化、多元化與競爭性給廣東省的工業發展帶來顯著正向影響，與表2預期經濟意義一致。勞動力投入彈性和各項知識溢出彈性顯著提高，物質資本投入彈性大大降低，表明當模型考慮空間相關性的影響時，勞動力投入和一定程度的知識溢出對產業經濟增長的貢獻作用增大，勞動力和物質資本的跨區域流動因素、產業專業化、多元化以及競爭外溢得以體現。

對于空間相關性的評估，SEMA和HSEMA模型衡量一個地區產業內部誤差沖擊效應的空間誤差移動平均系數θ分別為0.8072和0.7068，說明一個地區產業中具有非常強的局部空間相關性，某一產業受到其過去以及該地區內部各產業未被考慮到的新息沖擊效應的影響較大。HSEMA模型在考慮空間相關性的基礎上同時考慮數據中的層級結構，θ的估計值與SEMA模型相比有所降低，空間誤差移動平均系數θ、勞動力投入、物質資本投入和知識溢出指標彈性均得到修正。

此外，SEMA模型給出了衡量所有地區全體產業隨機效應的標準差（波動率）為σμj=0.3702。HSEMA模型給出了衡量地區間的差異程度的地區層級隨機效應標準差為σαi=0.2260，以及考慮產業嵌套于地區中，衡量產業間的差異程度的產業嵌套隨機效應的標準差為σμij=0.2146，說明地區隨機效應差異程度和嵌套隨機效應差異程度可被識別。可以發現，當考慮數據層級結構的影響，σμij＜σμj，按地區分組后組內產業差異程度σμij較所有地區全體產業混合的產業差異程度σμj下降，即組內相似性得到提高，使得SEMA模型在一定程度上得到修正。不難看出，采用同時考慮空間誤差移動平均和嵌套隨機效應的HSEMA模型更好，模型估計結果更為符合經濟現實。

使用HSEMA模型對廣東省工業產業知識溢出效應的實證研究發現，勞動力和物質資本投入、產業專業化、多元化以及競爭外溢對產業發展起到正向促進作用，且具有相當強的產業局部空間相關性。在研究對象存在層級結構與空間相關的情況下，與SEMA模型相比，HSEMA模型能識別地區間差異，并進一步修正產業間差異。

五、結論

本文構建了可同時考察數據層級效應與空間誤差移動平均系數的HSEMA模型，其誤差項可以分解成兩類層級隨機效應，分別是地區隨機效應以及產業嵌套于地區中的嵌套隨機效應。基于廣義矩估計框架，得出HSEMA模型的18個矩條件元素，由此得到各參數的GMM-FGLS估計量。實例分析表明，模型適用于三維非平衡面板數據，并對傳統計量經濟學模型的估計結果進行了修正，能更好地反映實際經濟運行特征。

文章推進了空間多層次誤差模型關于空間誤差局部相關估計的研究，與HSLAG模型、HSEAR模型可以相互補充，完善了同時具有層級結構與空間效應數據模型的估計方法研究，為經濟管理研究提供了新的研究思路。對于后續探索，可研究空間多層次模型的檢驗統計量；考慮數據的地理坐標，結合地理加權回歸重塑空間多層次模型，對其參數估計量與檢驗統計量進行推導，側重研究層級數據的空間異質性。