基于渦流效應的線圈陣列傳感器設計與神經網絡檢測算法

，，

(江蘇大學 電氣信息工程學院，鎮江 212000)

鋼筋混凝土結構相較于其他建筑結構具有堅固耐用，承重性好、抗剪切性強以及造價低廉等優點，被大量應用于日常生活中。對于鋼筋混凝土結構進行檢測具有較高的經濟價值及社會意義，而鋼筋質量與結構整體質量有較大關系，因此對混凝土內部鋼筋進行檢測尤為重要。

目前，對于混凝土內部鋼筋的檢測方式主要有破墻檢測和無損檢測。破墻檢測方式具有直觀精確的優點，但檢測的同時會對結構造成損傷；無損檢測可在不破壞結構的情況下完成檢測。應用于混凝土鋼筋檢測的無損檢測方法包括超聲波法，電磁法，射線法等，因其不會對被檢測物造成損害，是發展最為迅速的檢測方法之一[1]。

鋼筋檢測裝置多采用電磁法中的渦流檢測法。渦流檢測具有裝置小型化、易于操作、檢測速度快、精度高等優點。但由于渦流檢測裝置的結構一般都較為簡單，對于鋼筋直徑的檢測存在困難，使用上還是存在局限性[2]。

筆者提出了一種基于線圈陣列的檢測方式，將過去較為簡單的兩個線圈變為多個線圈，按一定結構排列，并采用脈沖渦流檢測方式以提高檢驗效率。該方法在完成鋼筋定位和保護層厚度檢測的同時，也能測量鋼筋直徑，通過軟件仿真和試驗，驗證該檢測方案具有一定的可行性。

1 渦流檢測

渦流檢測的主要理論依據為電磁感應原理。當導體在磁場中運動，或者處在變化的磁場中時，導體內部會產生自成閉合回路的感應電流，稱為渦流[2]。因渦流是瞬變的，自身也會產生瞬變的磁場，檢測線圈受到該磁場的影響會產生阻抗的變化，通過這部分變化就可以得到鐵磁性被檢測物的部分性能指標。

渦流檢測的優點有：檢測時無需接觸試件，且不需要耦合介質；檢測速度快；由于導體和非導體的磁導率不同，渦流檢測能檢測金屬覆蓋層或非金屬保護層的厚度；檢測信號為電信號，有利于檢測結果的數字化處理。

1.1 正弦渦流測厚

渦流測厚技術利用的原理是渦流效應中的提離效應。當線圈靠近導體試件時，線圈阻抗變化不僅與導體試件的磁導率、檢測頻率等因素有關，同時還受到線圈至試件表面距離變化的影響[3]。

傳統渦流測厚采用的是單一激勵頻率的正弦波。由于較高的激勵頻率可增大試件中由激勵產生的渦流密度，進而增強渦流檢測的提離效應，且可以抑制由于電導率變化所產生的影響，故工作頻率一般都較高。渦流滲透入導體的距離，通常稱為滲透深度，其同樣受到激勵頻率的影響。當渦流密度衰減到其表面值的1/e時的滲透深度稱為標準滲透深度δ，其公式為

(1)

式中：f為激勵頻率；μ0為真空磁導率，一般取μ0=4π×10-7H·m-1；μr為相對磁導率；σ為電導率。

一般將標準滲透深度的2.6倍作為最大滲透深度，并以此衡量儀器所能檢測的最大深度e[4-5]。

通過式(1)可以看出，標準滲透深度與激勵頻率成反比關系，激勵頻率越高，所能檢測的深度越有限。

1.2 脈沖渦流陣列檢測

脈沖渦流檢測的激勵信號采用的是具有一定占空比的方波信號。根據傅里葉信號展開理論，脈沖渦流相比于傳統的正弦渦流具有更為豐富的頻譜特性，所攜帶的試件信息也更為豐富[6-7]。

渦流陣列的特點在于多線圈以特定方式排列，由于在不同位置上，不同特性的線圈所受到的脈沖渦流磁場的影響存在差別，故可通過多個線圈激勵與檢測的方式獲得鋼筋直徑與保護層厚度的信息，從而解決鋼筋直徑檢測的問題[8]。

2 神經網絡

神經網絡具有極強的非線性擬合能力，且學習規則簡單，有較強的魯棒性和記憶性，具有強大的自學習能力[9-10]，常見應用領域涵蓋了醫學應用、經濟金融預測、圖像處理以及工業控制等多種場合。

BP(Back Propagation)神經網絡也稱誤差反向傳遞神經網絡，其特點在于信號正向傳遞，誤差反向傳遞，其結構模型示意如圖1所示。其優點在于將誤差分攤給各個節點，易獲得誤差信號，進而可對權值進行有效修改。BP神經網絡采用多層網絡結構，大致可將其分為3層，即輸入層、中間層(隱含層)和輸出層；其中輸入層與輸出層固定為1層，而隱含層可有1層或多層，層與層的節點之間以權的方式連接，層內部節點無連接。

圖1 BP神經網絡結構模型示意

相較于其他形式的神經網絡，BP神經網絡由于采用多層結構方式，理論上可以逼近任意非線性函數。

3 檢測系統構成

檢測系統的組成主要包括3個部分：線圈傳感器部分、硬件電路部分以及單片機部分。線圈傳感器部分采用脈沖渦流陣列傳感器，特點在于使用多個不同電感、形狀和匝數的線圈，按照一定結構進行傳感器設計，相較于傳統渦流傳感器，脈沖渦流陣列傳感器可產生更多的激勵信號和檢測信號，有利于鋼筋的相關檢測，在文中，線圈結構的排列組合方式在鋼筋定位中起到了至關重要的作用。硬件電路部分的主要作用在于放大濾波處理。單片機模塊采用STM32單片機。

3.1 線圈傳感器設計

采用脈沖渦流檢測陣列的方式，檢測裝置由8個線圈組成，其中一個為激勵線圈A，3個主檢測線圈為B1，B2，B3，4個定位及輔助檢測線圈C1，C2，C3，C4。為了驗證方案的合理性，采用ANSOFT MAXWELL軟件進行模型仿真，線圈陣列結構示意如圖2所示。

圖2 線圈陣列結構示意

裝置激勵信號采用脈沖激勵，脈沖激勵的優點在于具有豐富的頻率成分，可兼顧檢測深度和檢測精度，且方波的獲取相較于諧波更為簡單。

3.2 硬件電路設計

硬件電路主要分為兩部分，激勵部分和信號放大部分。激勵部分電路采用單片機驅動的MOS管(場效應晶體管)電路，由于STM32管腳驅動能力有限，故采用MOS管控制激勵線圈的通斷，以產生矩形波信號作為激勵信號。

信號放大電路主體為比例放大電路，輸入信號為各個檢測線圈的響應信號，共7組。

3.3 單片機部分設計

采用的控制器為STM32單片機。STM32單片機具有高性能、低成本、低功耗等優點，大量應用于工業領域。

STM32單片機作為硬件電路中激勵部分的驅動來源，可較為方便地通過PWM(脈沖寬度調制)方式產生矩形波信號。此外，該單片機具有較多的管腳資源，3個ADC(模數轉換器)模塊，共16個外部通道，滿足渦流脈沖檢測信號較多的需求。

經ADC采樣完成后的數字信號經STM32單片機進行累加處理，并通過自帶串口輸出上位機進行數據處理[12]。

4 試驗過程

4.1 檢測裝置與響應信號

圖3為檢測裝置實物外觀。

圖3 檢測裝置實物外觀

圖4為試驗的激勵信號，圖5為檢測線圈B1在無鋼筋情況下的響應信號，圖6為檢測線圈B1在有鋼筋情況下響應信號。

圖4 試驗的激勵信號

圖5 檢測線圈B1無鋼筋情況下的響應信號

圖6 檢測線圈B1在有鋼筋情況下的響應信號

如圖4所示，tb時刻為激勵下降沿產生的時刻，tp為激勵上升沿產生的時刻。對比圖5和圖6可知，混凝土保護層厚度以及鋼筋直徑對于信號的影響主要體現在激勵下降沿tb時刻開始至響應信號歸零時刻tp這一區間內，即激勵信號的低電平區。由圖6可知，當檢測區域內有鋼筋存在時，該區域檢測信號明顯下移，檢測線圈瞬態感應電壓產生變化。考慮到計算方便，采用積分方式將下降沿時刻至歸零時刻信號的積分s作為特征量，公式為

(2)

式中：U(t)為檢測信號。

積分后的s可較好地表述信號，且有利于減少樣本數量，方便單片機處理。

STM32單片機自帶12位ADC，可采集經放大濾波后的脈沖渦流響應信號，累加后得到一個無量綱量S，其意義等同于式(2)中的s。

4.2 保護層厚度與直徑檢測

圖7為檢測線圈B3在高度分別為5，15，30，45，60 mm，鋼筋直徑分別為6，8，10，12，14，16，18，22，25 mm時，單片機采樣輸出信號并累加的結果。

圖7 不同高度、不同鋼筋直徑時的B3線圈信號累加結果

圖8 不同高度、不同鋼筋直徑時的B2線圈信號累加結果

圖8為檢測線圈B2在高度分別為5，15，30，45，60 mm，鋼筋直徑分別為6，8，10，12，14，16，18，22，25 mm時，單片機采樣輸出信號并累加的結果。

結合圖7和圖8可知，信號S與保護層厚度L成正比，與鋼筋直徑D成反比，均呈現單調性。假設檢測線圈B3采樣累加值為SB3，則存在函數f(D，L)=SB3，其解分別為(D1，L1)，(D2，L2),…,(Dn，Ln)。同理，當檢測線圈B2采樣累加值為SB2時，存在函數g(D，L)=SB2，其解分別為(1，1)，(2，2),…,(n，n)，其中必然存在一點(Dx，Lx)，使得(Dx，Lx)=(y，y)，此時Dx即為鋼筋直徑，Lx即為混凝土保護層厚度。

4.3 鋼筋定位

目前常見的鋼筋定位方式為差動連接方式(見圖9)。差動連接方式是將兩個線圈反向串聯，當鋼筋處于兩個線圈中間位置時，兩線圈產生方向相反、大小相同的響應信號，反向串聯后輸出為0，具有定位準確的優點。但是其缺點在于線圈數量少，當鋼筋處在線圈組的中心點時，無論鋼筋是何走向，輸出均為0，故僅能對鋼筋進行簡單定位，而對于鋼筋角度的偏差不敏感。

圖9 差動連接方式示意

定位線圈為4個獨立線圈，圖10為鋼筋與線圈陣列位置示意。

圖10 鋼筋與線圈陣列位置示意

圖11 鋼筋定位信號累加結果

圖11為鋼筋定位信號累加結果。當鋼筋處于檢測線圈C1正下方時，存在SC1>SC2；當鋼筋處于檢測線圈C2正下方時，存在SC2>SC1。由于線圈呈對稱性排列，故C3，C4線圈的信號類似。故可通過4個檢測線圈之間的大小關系對鋼筋所在位置進行判定，當且僅當SC1=SC2=SC3=SC4時，鋼筋位于裝置正下方，且與裝置長邊平行走向，具有定位準確，可對鋼筋走向進行檢測的優點，從而解決了目前儀器對于鋼筋角度偏差不敏感的難題。

5 建立神經網絡模型

BP神經網絡一般采用3層結構，即輸入層、隱含層和輸出層。其中隱含層節點數量會對神經網絡的準確性產生較大影響。隱含層節點數量過多易產生過擬合現象，節點數量過少，網絡精度不足。隱含層節點數選擇規律一般遵循如下公式

(3)

式中：l為隱含層節點數；n為輸入層節點數；m為輸出層節點數；a為0～10之間的常數。

神經網絡隱含層節點數設置為8，迭代次數設置為100，誤差目標設置為0.000 1,神經元激勵函數為

(4)

采用MATLAB軟件神經網絡工具箱所提供的函數，newff函數創建BP神經網絡，其函數格式為newff[PR,(S1,…,Sn),(TF1,…,TFn),BTF,BLF,PF]，PR為R個輸入向量的范圍，即一個R*2的矩陣；Si為第i層的節點數；TFi為第i層的傳遞函數；BTF為訓練函數；BLF為學習函數；PF為性能函數。

將目前采集到的4 042組數據隨機劃分為兩組，訓練數據共3 900組，用于網絡訓練，驗證數據142組，用于檢測神經網絡精度。

通常情況下，建立一個多輸入多輸出的神經網絡便可對變量進行有效識別。但若采用一個兩輸入兩輸出的BP神經網絡，對于鋼筋保護層厚度識別效果非常差，猜想可能是由于鋼筋直徑對于渦流信號的影響以及混凝土保護層厚度對于渦流信號的影響的相互耦合，以至于對于保護層厚度的識別效果不佳。基于該猜想，采用建立兩個多輸入單輸出的神經網絡方案，經驗證對混凝土保護層厚度和鋼筋直徑具有一定的識別效果。

由于BP神經網絡對于鋼筋直徑識別準確度較高，故首先建立神經網絡network1，其輸入為采樣的渦流信號積分組，輸出為鋼筋直徑的預測值(見圖12)，表1為直徑預測的部分數據。

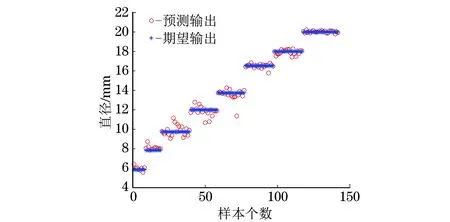
圖12 鋼筋直徑預測結果

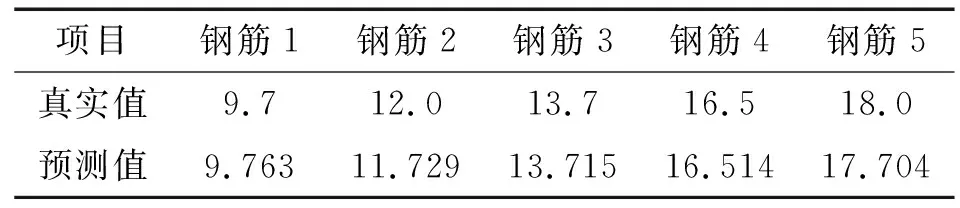
表1 鋼筋直徑預測結果的部分數據 mm

由神經網絡network1可獲得鋼筋直徑預測值，將其和采集的渦流信號數據作為3個輸入量，建立3個輸入量，1個輸出量的神經網絡network2，其輸出為保護層厚度的預測值(見圖13)，表2為保護層厚度預測值的部分數據。

圖13 保護層厚度預測結果

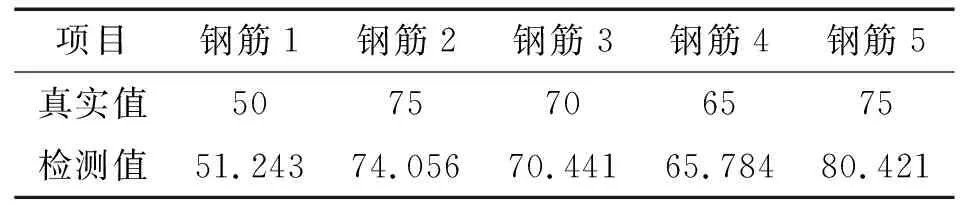
表2 保護層厚度預測結果的部分數據 mm

6 神經網絡結果分析

均方根誤差(RMSE)是反映神經網絡預測輸出精度的常見衡量指標，均方根誤差越小，預測輸出和實際輸出越吻合，其計算公式為

(5)

式中：RMSE為均方根誤差；Xobs,i為預測輸出；Xmodel,i為期望輸出。

試驗裝置測得保護層厚度的預測均方根誤差約為1.38，其誤差范圍在-3 ～5 mm之間(見圖14)。鋼筋直徑預測均方根誤差約為0.90，其誤差范圍約在-2.5～1.5 mm之間(見圖15)。考慮到課題需同時兼顧混凝土保護層厚度的預測與直徑的預測，且受限于目前樣本量較小(在大數據量訓練時，可進一步提高檢測精度)，以及實驗室測量儀器精度誤差等原因，故該測量精度可接受。

圖14 保護層厚度預測誤差

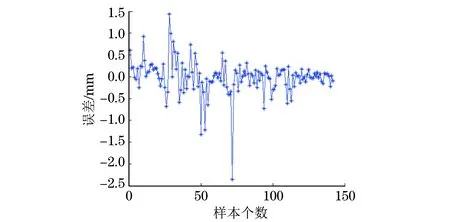
圖15 鋼筋直徑預測誤差

7 結語

基于脈沖渦流陣列理論，設計了一種多線圈結構裝置。通過軟件仿真，得出鋼筋的位置、直徑和保護層厚度均對檢測線圈中的脈沖渦流響應信號有影響，并通過試驗，驗證了仿真結果的正確性。試驗中采集不同位置、不同保護層厚度、不同直徑的鋼筋數據，采用建立并訓練神經網絡的方式獲得數學模型，彌補了目前同類型產品不能準確定位缺陷，以及無法對鋼筋直徑進行有效檢測的不足，對脈沖渦流檢測相關儀器的研制具有指導意義。