伯特蘭悖論解析

杜國平

(中國社會科學院 哲學研究所， 北京 100732)

伯特蘭悖論自提出以來，受到了人們廣泛的關注。本文不擬對相關研究進行綜述和評論，而只是從問題本身出發，使用邏輯方法來分析問題本身的推理結構，并對悖論問題產生的根源進行純粹理論的闡述，以期澄清某些哲學論爭。

一、伯特蘭悖論概述

伯特蘭悖論是由法國數學家約瑟·路易斯·弗朗索瓦·伯特蘭(Joseph Louis Fran?ois Bertrand)于1889年提出的一個概率悖論[1]。該悖論的基本結構是：

對于問題“圓內任意一條弦，其弦長長于該圓內接等邊三角形邊長的概率是多少？”伯特蘭給出了3個不一致的答案[2]。

第1種解答：考察從圓上任意一點A出發的那些弦(見圖1)。以A為一個頂點作圓內接等邊三角形ABC。如果弦的另一端落在∠DAB或者∠EAC的區域內(包括B、C兩點)，如弦AA1，則弦長并非長于該圓內接等邊三角形的邊長；如果弦的另一端落在∠BAC的區域內(不包括B、C兩點)，如弦AA2，則弦長長于該圓內接等邊三角形的邊長。反之亦然。因為△ABC是等邊三角形，∠BAC等于60°，所以弦長長于該圓內接等邊三角形邊長的概率是：

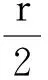
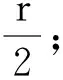
伯特蘭悖論的基本結構是：考慮弦長長于圓內接等邊三角形邊長的概率，根據無差別原則，分別得出了3個不同的結論，而這3個結論是不一致的。

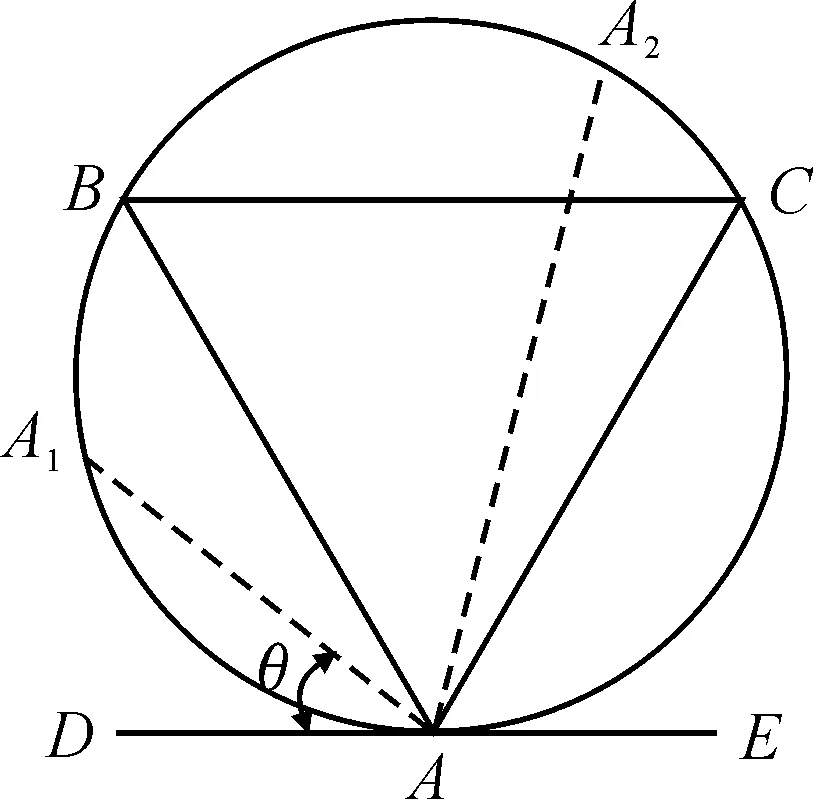
圖1

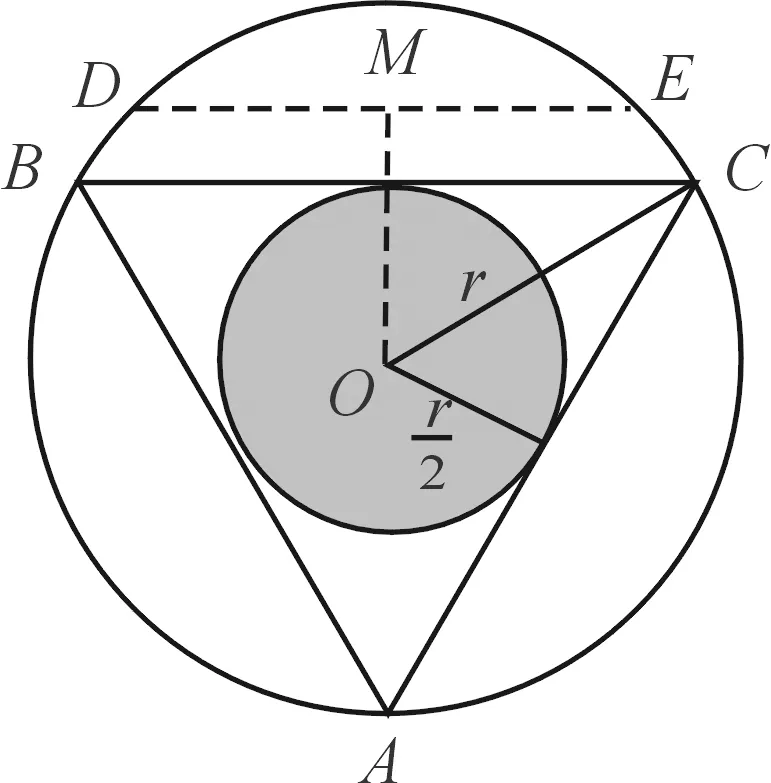
圖2

圖3

伯特蘭悖論所直接拷問的是主觀概率的合理性問題。具體地說，它拷問的是主觀概率無差別原則的合理性。無差別原則(the principle of indifference)指的是：對于某一條件下的若干種可能性，如果沒有證據證明其中的某一種可能性比其他的可能性更大或者更小，那么我們賦予這些可能性以相同的概率[3]。伯特蘭悖論的發現和提出，對使用無差別原則來確定主觀概率的方法構成了一個極其嚴重的挑戰。

二、伯特蘭悖論的拓展示例

為了進一步凸顯伯特蘭悖論的特性，我們可以對伯特蘭悖論加以更進一步的引申。

伯特蘭悖論中提出的問題是：“在一個圓內任意拉一條弦，這條弦長于這個圓內接等邊三角形邊長的概率P(c)是多少？”對于這一問題，除了上述3種解答之外，我們還可以給出其他幾種解答。

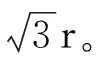
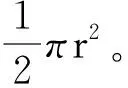
第5種解答，雖然角度與第4種解答有所不同，但是其結果是相同的。

類似地亦可考慮由弧AB形成的扇形面積的情況。

后面將進一步表明，按照上述思路，對于這一問題，任意值的概率都是可以給出的。

三、弦長與其相關變量之間的多項式關系

圖4

1.弦AB的長度x與∠DAB度數θ之間的關系見圖4。

不難看出，弦AB的長度x與∠DAB度數θ之間存在如下關系：

2.弦AB的長度x與以O為圓心、以弦中點到圓心距離為半徑的圓面積S1之間的關系為：

3.弦AB的長度x與弦中點到圓心距離y之間的關系為：

4.弦AB的長度x與弦AB和弧AB(較短的一段弧)圍成的封閉圖形面積S2之間的關系為：

5.弦AB的長度x與弦AB和弧AB(較長的一段弧)圍成的封閉圖形面積S3之間的關系為：

四、多項式關系解析

如果我們將上述討論歸納到表1中，則不難看出其中的一般性問題。

表1 弦長與其相關變量之間的多項式關系

弦長相關變量關系多項式(f(x))f (0)f (3r)f (2r)特征區間概率xxx03r2r(3r,2r]2-32x∠DAB度數θ arcsinx2r060°90°(60°,90°]13x弦中點所在圓面積π(r2-x24)πr2πr240[0,πr24)14x弦中點到圓心距離r2-x24rr20[0,r2)12x弦和弧圍成的封閉圖形面積aecsinx2r180πr2-x2r2-x240πr23-3r24πr22(πr23-3r24, πr22]2π+336π

注：(1)特征區間指的是弦AB的長度x長于內接等邊三角形的邊長時，關系多項式(f(x))的值域; (2)概率指的是弦AB的長度x長于內接等邊三角形的邊長時，相關變量的概率，而不只是弦AB的長度x長于內接等邊三角形的邊長的概率

對于與弦長x相關的變量f(x)，按照悖論構造的思路，其時得到的弦AB的長度長于內接等邊三角形邊長的概率是：

由此我們不難得到這一問題的任意概率值。例如如果相關變量為：

實際上，如果希望得到的概率值為n，只需其相關變量f(x)滿足下列條件即可：

由此可見，伯特蘭悖論是由不同的相關變量造成的。伯特蘭在構造悖論的過程中，得出的不同概率只是不同的相關變量的概率，而不是弦長長于內接等邊三角形邊長的概率。

五、類伯特蘭悖論及其解釋

為了彰顯伯特蘭悖論的問題所在，可以構造如下的類伯特蘭悖論。

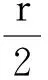
問：落在O1內的數字幣完全落在O2內的概率是多少？

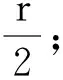
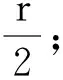
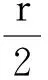
由1、2、3可知，上述思想實驗的結果形成了一個類伯特蘭悖論。

S=πx2

六、結論

由前述討論分析，我們可以得出如下結論：

因此由p得出矛盾，從而p不成立。這看似對無差別原則形成了質疑。

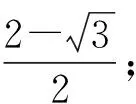
據此并不能由p得出矛盾。

因此，伯特蘭悖論并不是一個悖論，它對無差別原則也并不能構成質疑。

2.對于定義域為[0,m]的變量x，當考察其特征域[n,m]的概率時，我們只能根據變量及其特征域自身的情況，依據無差別原則來進行考察，而不應將其相關的函數所對應的特征域及其在值域中的概率來進行變換。這是因為變換所得到的概率只是相應的函數的概率，而可能不是自變量原初的概率了。根據無差別原則，變量x本身的概率是唯一的。同樣根據無差別原則，與變量相應的一個函數的概率也是唯一的；但是與變量相應的不同函數的概率可能是不同的，并且由于函數的不同，其各種值的概率都是可能的，具體概率值的多少是由函數的性質決定的[4]。

3.伯特蘭悖論存在概念混淆的邏輯錯誤。其中，混淆了變量本身的概率和變量相應的函數的概率。

4.邏輯分析有助于厘清概念、明確判斷，并進而分析推理結構、消解悖論。