淺談原創(chuàng)試題對課堂教學(xué)的作用

安徽 蔣玉芳 張 威

原創(chuàng)試題與課堂教學(xué)其實是相輔相成的.從課堂的學(xué)生探究活動中、從課堂教學(xué)里的“失敗處”、從學(xué)生巧妙的回答中都可以獲取原創(chuàng)試題的素材.同樣原創(chuàng)試題對課堂教學(xué)也有著非常重要的作用.因為不同層次的學(xué)生、不同階段的學(xué)生所需求試題的難度是不同的.每個學(xué)生都有適合自己的試卷、習(xí)題，當(dāng)學(xué)生與題搭配成功時，那么此題將使學(xué)生的學(xué)習(xí)效果達到最大化.所以筆者認為在平時的教學(xué)中，教師應(yīng)該多一些原創(chuàng)題，這樣才能使得學(xué)生和題搭配成功，這樣的課堂才會更高效.那么原創(chuàng)題對課堂教學(xué)到底有哪些具體的作用呢？以下是筆者的個人感受.

一、鞏固新知，激發(fā)學(xué)生學(xué)習(xí)的興趣

一線教師都知道，在講授新知時，需要尋找典型例題對新知進行詮釋，而往往教輔或教材上的例題或習(xí)題并不適合自己所教授的學(xué)生，此時需要一道既能讓學(xué)生鞏固新知，又能適合當(dāng)前學(xué)生難易梯度的典型例題.那么什么樣的試題才算是一道典型例題呢？一道典型例題應(yīng)該不是所有學(xué)生都難以“下咽”的苦果，恰好相反，應(yīng)該是所有學(xué)生“品嘗”時感覺有話可說、有話要說的“菜肴”.典型例題不僅要能鞏固新知，同時也要能增強學(xué)生的學(xué)習(xí)自信心，激發(fā)學(xué)生的學(xué)習(xí)興趣.這就需要教師根據(jù)自己學(xué)生的實際情況命制試題.

例如，教師在講解函數(shù)f(x)=Asin(ωx+φ)+b(A,ω>0,

φ,b∈R)的圖象和性質(zhì)時，有些基礎(chǔ)弱的學(xué)生對如何求A,ω,φ,b的值掌握得不好.特別對代入特殊點求φ時，為什么要強調(diào)最好代最值點，而不是零點百思不得其解.此時就需要一道適合他們且有針對性的題目來鞏固，同時激發(fā)他們的學(xué)習(xí)興趣.這時教師可以原創(chuàng)一道.

( )

【命題意圖】此題以生活中的實際物體為模型，極大地激發(fā)了學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣.從能力角度來看，此題不僅培養(yǎng)了學(xué)生閱讀理解能力，而且也培養(yǎng)了學(xué)生數(shù)據(jù)處理和計算能力.從知識層面來看，此題突出了教師的實際意圖，同樣更好地詮釋了A,ω,φ,b的實際意義.

【原創(chuàng)例題2】已知函數(shù)f(x)=2sin(2x+φ)(-π<φ<π)的部分圖象如圖所示，則φ=________.

【命題意圖】此原創(chuàng)題的圖象和以往的陳題圖象差別很大，其用意就是“引導(dǎo)”學(xué)生代零點求φ，讓學(xué)生“真正地”犯一次錯.此題不僅培養(yǎng)了學(xué)生的數(shù)形結(jié)合思想，而且也培養(yǎng)了學(xué)生轉(zhuǎn)化與化歸的數(shù)學(xué)思想.

【點評】此時有的學(xué)生不去考慮增根問題，那么就錯了.若有學(xué)生想到增根問題，又要花時間去排除增根.那么通過代入最值點，是否就不會出現(xiàn)增根呢？請看下面【正解】.

二、突破教學(xué)重難點，使課堂教學(xué)更高效

教師在講授新課時，會發(fā)現(xiàn)有些重難點僅靠對概念的細化講解，達不到預(yù)想的效果，此時需要配備例題進行具體化，讓學(xué)生由淺入深，但是如果配備的例題不得當(dāng)，沒有充分考慮到學(xué)生的認知能力，學(xué)生的理解和掌握依然會遇到困難.而教師在充分了解當(dāng)前學(xué)生實際水平的情況下，命制的例題就再合適不過了.同時作為命題者，在講解此題時必能更透徹，因為他比別人更理解此題的本質(zhì)，以及思考的方向.如：幾何體的外接球問題一直是高考的重點和難點，而學(xué)生在求幾何體的外接球半徑時，往往會“有話說，但又說不到點子上”.如筆者設(shè)置的如下原創(chuàng)題.

筆者知道如果把這樣一道題“甩出去”，估計很多學(xué)生都無法做出.于是筆者進行如下設(shè)置.

(Ⅰ)請過BD中點作出二面角A-BD-C的平面角，并說明理由；

(Ⅱ)分別確定△ABD，△BCD的外接圓圓心O1,O2位置；

(Ⅲ)作出三棱錐A—BCD的外接球球心O，并說明理由；

(Ⅳ)求出三棱錐A—BCD的外接球半徑.

【命題意圖】進行這樣的原創(chuàng)設(shè)置，不僅充分展現(xiàn)了題目的逐層遞進，而且更讓學(xué)生在由淺入深，輕松的氛圍中掌握知識.在能力層面上，培養(yǎng)了學(xué)生空間想象能力和數(shù)據(jù)處理能力以及應(yīng)用意識.在知識層面上，考查了二面角的平面角定義，三棱錐的外接球含義.

【點評】本題是在任何教輔資料、各省模擬題、高考真題中都不會出現(xiàn)的，如果直接用【原創(chuàng)例題3】進行教學(xué)，雖然考查的內(nèi)容一樣，但是對難點、重點突破不了.而【原創(chuàng)例題4】能通過四問完美的突破難點、重點，而且讓學(xué)生真正掌握這一類題型的通法.

三、及時引導(dǎo)和糾正學(xué)生錯誤的思維過程

由于學(xué)生的思維不受課堂的制約，所以課堂教學(xué)設(shè)疑和提問的過程中，往往會出現(xiàn)意想不到的回答，但是正是這樣的回答恰好體現(xiàn)了學(xué)生思維過程的真實性.如果不能加以合理的引導(dǎo)和糾正，這種思維將會在學(xué)生腦海中根深蒂固.而此時需要教師的原創(chuàng)試題來“對癥下藥”，從而更好地引導(dǎo)和糾正這種錯誤的思維過程.如：在講授函數(shù)零點解答題時，學(xué)生由于受到小題數(shù)形結(jié)合的影響，常常用數(shù)形結(jié)合思想求解零點問題，為了引導(dǎo)和糾正這一問題，筆者命制了如下原創(chuàng)例題.

【原創(chuàng)例題5】已知函數(shù)f(x)=ex-2x-a(a∈R).

(Ⅰ)求函數(shù)f(x)的單調(diào)性；

(Ⅱ)討論函數(shù)f(x)零點個數(shù).

【分析】(Ⅰ)略解：f(x)在(-∞,ln2)上單調(diào)遞減，在(ln2,+∞)上單調(diào)遞增.

(Ⅱ)由于受到小題數(shù)形結(jié)合的影響，在學(xué)生中出現(xiàn)一種不規(guī)范的解答：

因為函數(shù)f(x)的零點個數(shù)即為方程ex-2x-a=0的實根個數(shù)，

即表示函數(shù)g(x)=ex-2x與y=a的交點個數(shù)，

由(Ⅰ)可知f(x)在(-∞,ln2)上單調(diào)遞減，在(ln2,+∞)上單調(diào)遞增，

且g(x)min=2-2ln2，如圖所示.

當(dāng)a<2(1-ln2)時，函數(shù)f(x)在R上無零點；當(dāng)a=2(1-ln2)時，函數(shù)f(x)在R上有1個零點；當(dāng)a>2(1-ln2)時，函數(shù)f(x)在R上有2個零點.

【點評】此題第二問，乍一看學(xué)生的解法，好像無懈可擊，其實此解法極其不規(guī)范，因為學(xué)生是用函數(shù)的性質(zhì)去畫函數(shù)的圖象，此時得到函數(shù)的圖象本身就是不嚴謹?shù)模钟煤瘮?shù)的圖象去解決函數(shù)的有關(guān)性質(zhì)問題，這就更不規(guī)范.在高考中作為解答題是要被扣很多分的.

【正解】因為函數(shù)f(x)的零點個數(shù)即為函數(shù)圖象與x軸交點的個數(shù)，

由(Ⅰ)可知f(x)在(-∞,ln2)上單調(diào)遞減，在(ln2,+∞)上單調(diào)遞增，

且f(x)min=2-2ln2-a，

當(dāng)a<2(1-ln2)時，f(x)>0恒成立，此時函數(shù)f(x)在R上無零點；

當(dāng)a=2(1-ln2)時，f(x)≥0恒成立，當(dāng)且僅當(dāng)x=ln2時取得等號.

此時函數(shù)f(x)在R上有1個零點；

當(dāng)a>2(1-ln2)>0時，則f(ln2)<0，

所以函數(shù)f(x)在(-∞,ln2)上有且只有1個零點；

又因為f[ln(3a+2)]=eln(3a+2)-2ln(3a+2)-a=2[a+1-ln(3a+2)]，

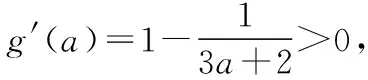
所以g(a)>g(0)=1-ln2>0，所以f[ln(3a+2)]>0，又因為ln(3a+2)>ln2，

即可得f(ln2)·f[ln(3a+2)]<0，又因為f(x)在(ln2,+∞)上單調(diào)遞增，

所以此時函數(shù)f(x)在(ln2,+∞)上有且只有1個零點；

故函數(shù)f(x)在R上有2個零點.

綜上所述,當(dāng)a<2(1-ln2)時，函數(shù)f(x)在R上無零點；當(dāng)a=2(1-ln2)時，函數(shù)f(x)在R上有1個零點；當(dāng)a>2(1-ln2)時，函數(shù)f(x)在R上有2個零點.

【點評】此解法完全符合高考標(biāo)準(zhǔn)答案的解法，完全糾正學(xué)生做任何題都想采用數(shù)形結(jié)合思想進行解題的套路，同時引導(dǎo)學(xué)生做解答題時，解題過程一定要規(guī)范.

當(dāng)筆者認為此題應(yīng)該告一段落時，在課下有個學(xué)生找到我，就此題提出了一些疑問：如果是客觀題時，用數(shù)形結(jié)合思想進行解題非常簡便，但是怎么就能確定函數(shù)的圖象在無限趨近-∞和+∞時，函數(shù)的圖象就一定趨近+∞呢？有沒有可能趨近某個特定的值呢？有沒有這樣的例題呢？就學(xué)生提出的這些疑問筆者在第二天的課堂上講解了如下原創(chuàng)例題.

【原創(chuàng)例題6】已知函數(shù)g(x)=2x+mex(m∈R)存在兩個不同零點，則m的取值范圍是________.

【命題意圖】主要考查學(xué)生的數(shù)形結(jié)合思想、數(shù)據(jù)處理能力、轉(zhuǎn)化與化歸思想.同時在知識上主要是考查函數(shù)零點、函數(shù)圖象等問題.

【分析】作為客觀題，可以進行如下思考：

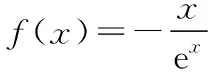
其實答案是錯的，原因是當(dāng)x趨近于+∞時，g(x)趨近于0，即函數(shù)的圖象為下圖：

【點評】通過此題的講解，能很大程度上引導(dǎo)學(xué)生解題時要有嚴謹?shù)膽B(tài)度.

四、提升學(xué)生分析問題和解決問題的能力

一線教師常常熱衷于數(shù)學(xué)例題的講解、解答示范和解題訓(xùn)練，但是教學(xué)效果往往出現(xiàn)低效現(xiàn)象——“聽得懂、想不到”的狀況，其原因在于學(xué)生沒有抓住或者深入挖掘此題的本質(zhì).而教師講解其個人命制的試題時，更容易讓學(xué)生理解命題意圖和題目本質(zhì).教學(xué)中充分結(jié)合學(xué)生的認知規(guī)律，設(shè)置不同梯度原創(chuàng)題，由具體到抽象，由易到難，形成知識的遷移，不斷提升分析和解決問題的能力.如：教師想讓學(xué)生掌握二次函數(shù)型函數(shù)零點問題，設(shè)置如下原創(chuàng)鞏固練習(xí)題.

【原創(chuàng)例題7】已知函數(shù)g(x)=8e(lnx)2-(2e+8)x|lnx|，f(x)=-2x2，則方程g(x)-f(x)=0的實根個數(shù)是________.

【分析】由方程g(x)-f(x)=0，學(xué)生很顯然能得到8e(lnx)2-(2e+8)x|lnx|+2x2=0，而對方程根的判斷，學(xué)生首先會想到能不能直接解方程，如果能解又該如何解呢？學(xué)生掌握的是一元一次方程、一元二次方程、指數(shù)方程、對數(shù)方程等解法，而對如此復(fù)雜的方程，又該如何解呢？那么此時學(xué)生就會思考原方程是不是可以進行變形轉(zhuǎn)化等，一步一步把學(xué)生推向正解的“彼岸”.

【原創(chuàng)例題8】已知函數(shù)g(x)=4e(lnx)2-(2em+4)x|lnx|+2mx2，則函數(shù)g(x)有5個不同的零點，則實數(shù)m的取值范圍是________.

【命題思路】重點考查學(xué)生數(shù)形結(jié)合思想，轉(zhuǎn)化與化歸思想，培養(yǎng)學(xué)生分析問題和解決問題的能力.在知識層面上，更好地體現(xiàn)函數(shù)圖象、函數(shù)零點的實際應(yīng)用.

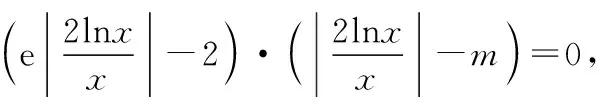
【點評】此題是在【原創(chuàng)例題7】的基礎(chǔ)上進行命制，充分展現(xiàn)了由易到難，形成知識的遷移，不斷地提升分析和解決問題的能力，同時進一步鞏固知識.也進一步說明只要真正理解題目的本質(zhì)，就能解決這一類型的題目，達到例題的真正典型作用.

五、有利于教師及時了解學(xué)生的學(xué)習(xí)情況和提升個人教學(xué)、解題的能力

教師給自己教授的學(xué)生命制試題時應(yīng)更注重鞏固目的、激勵目的和反饋目的.這樣才有利于幫助學(xué)生正確認識自我，有利于教師及時了解學(xué)生的學(xué)習(xí)情況，以便決定教學(xué)的起點與進度，決定教學(xué)內(nèi)容的深度與廣度.有利于教師改進教法，提高教學(xué)水平，進而提高教學(xué)質(zhì)量．同時教師在命制原創(chuàng)題時，都是經(jīng)過“選擇命題點—磨題—做題—修改—再磨題”的過程，而這個過程更是提升教師本人教學(xué)、解題能力的過程，只有不斷把這個過程延續(xù)下去，才能成為一名優(yōu)秀的教師.