薄壁硬殼式圓筒結構的屈曲分析

王驍峰，段 毅，袁銳之

(空間物理重點試驗室， 北京 100076)

硬殼結構是最簡單的薄壁結構[1]，圓柱筒殼由于特殊的幾何構型和優良的受力性能，被廣泛應用于船舶工程、導彈火箭外殼及航空航天等許多工程技術領域[2]，如火箭、導彈的儀器艙、貯箱、發動機燃燒室等。圓筒硬殼結構在火箭等飛行器的飛行過程中，飛行器艙段的薄壁圓筒殼受到軸向壓力往往會在強度破壞之前失穩(發生屈曲)，使飛行器的結構承載失效。均勻軸壓下圓柱薄殼的極限承載能力對初始幾何缺陷非常敏感。Tennyson[3]等人研究了局部軸對稱缺陷對圓柱薄殼屈曲性能的影響，指出局部缺陷會大大降低結構的承載性能。葉軍等的研究也表明[4]，環向初始缺陷是影響薄壁鋼桶臨界屈曲載荷的主要因素。

對于圓筒硬殼結構來說，由于加工工藝、加工誤差等原因，使得圓筒殼不可避免的存在幾何缺陷，即存在縱向和環向結構上的不對稱性，如焊縫、同軸度誤差、不圓度誤差以及局部凹凸不平等等，這種不對稱性導致臨界軸壓明顯降低。造成缺陷的原因還有存儲、運輸、安裝和使用等[5]。但加工誤差所造成的初始幾何缺陷是殼體承載能力下降的主要原因[6]。在進行殼體屈曲特性研究時，最為理想的情況是引入真實幾何缺陷，但是，由于殼體加工工藝不同，批次不同，產生的幾何缺陷也不同，即使同一批次產品的幾何缺陷也具有隨機性，這就需要通過大批量、相似殼體試驗，建立真實幾何缺陷的可靠性模型，往往費時費力，收效甚微[6]。因此，引入等效幾何缺陷的方法研究殼體屈曲特性就十分必要。Tennyson[3]研究局部軸對稱缺陷對鋼筒屈曲性能的影響時，發現即使只有一條軸對稱缺陷，也會使薄壁筒殼的屈曲臨界載荷有較大的降低，Koiter[7]首次研究了非完善殼體穩定性的一般準則，提出了“缺陷敏感度”的概念，揭示了屈曲的跳躍性與原始初始缺陷理論的相互關系。文獻[8]表明圓筒環向焊縫缺陷會導致最低的屈曲承載力，而缺陷最不利位置可通過無缺陷圓筒非線性屈曲模態確定[8]。歐洲法規EN1993-1-6(2007)[9]規定，幾何缺陷的形狀應取最差缺陷(即導致殼體屈曲載荷下降最快的缺陷)，在最差缺陷形狀未知的情況下，建議采用模態缺陷分析殼體的屈曲特性。

初始缺陷的形式一般分為特征值屈曲模態缺陷、環向焊縫缺陷、隨機缺陷、實測缺陷等[10]。對于結構的實際缺陷來說，在產品失效之前，無法預知缺陷的性質、位置和和缺陷程度，無法對后三種缺陷的屈曲問題進行前瞻性分析。工程上常常采用特征值屈曲模態缺陷進行分析，無需知道缺陷的性質、位置和和缺陷程度。對于殼體來說，只需給出殼體的線性特征值屈曲模態和一定百分比的殼體厚度作為初始幾何缺陷。對于網格加筋的圓筒結構、錐形圓筒結構等，求解殼體穩定性問題時，均可以當量成光壁圓筒結構[11]。本文研究表明，通過基于屈曲模態缺陷的非線性屈曲分析來求解圓筒結構的臨界失穩軸壓，用于工程設計是可行的。

1 非線性屈曲的描述

對于板、殼、桿、梁等結構，當其所受的外載荷達到一定值的時候，結構失穩，此時無需增大外載荷，甚至在外載荷減小的情況下，結構的變形繼續增大，即結構的剛度為零，甚至為負。隨著變形的增大，結構又開始恢復抵抗變形的能力，即結構發生了屈曲。第一次失穩發生前的過程稱為前屈曲，第一次失穩的后繼過程稱為后屈曲。

當結構處于理想狀態、無任何物理缺陷和幾何缺陷時，結構的彈性失穩表現為歧點(分岔點)失穩；對結構的屈曲分析可以用線性特征值描述，通過求解特征值可以確定結構的臨界失穩載荷。這個分析過程也是一個典型的前屈曲分析過程，如圖1中理想加載路徑所示。但實際結構不可能是理想結構，幾何不對稱因素(幾何缺陷)是不可避免的。結構的穩定性對初始幾何缺陷十分敏感，結構的失穩過程如圖1中所示非理想結構加載路徑。結構失穩的形式是駐點失穩，失穩的過程是一個幾何非線性過程，此時對屈曲過程的描述應采用非線性描述，由圖1可以看出，特征值屈曲的歧點所對應的臨界壓力值是非保守解，而結構的實際臨界壓力值應該是駐點所對應的臨界壓力值。

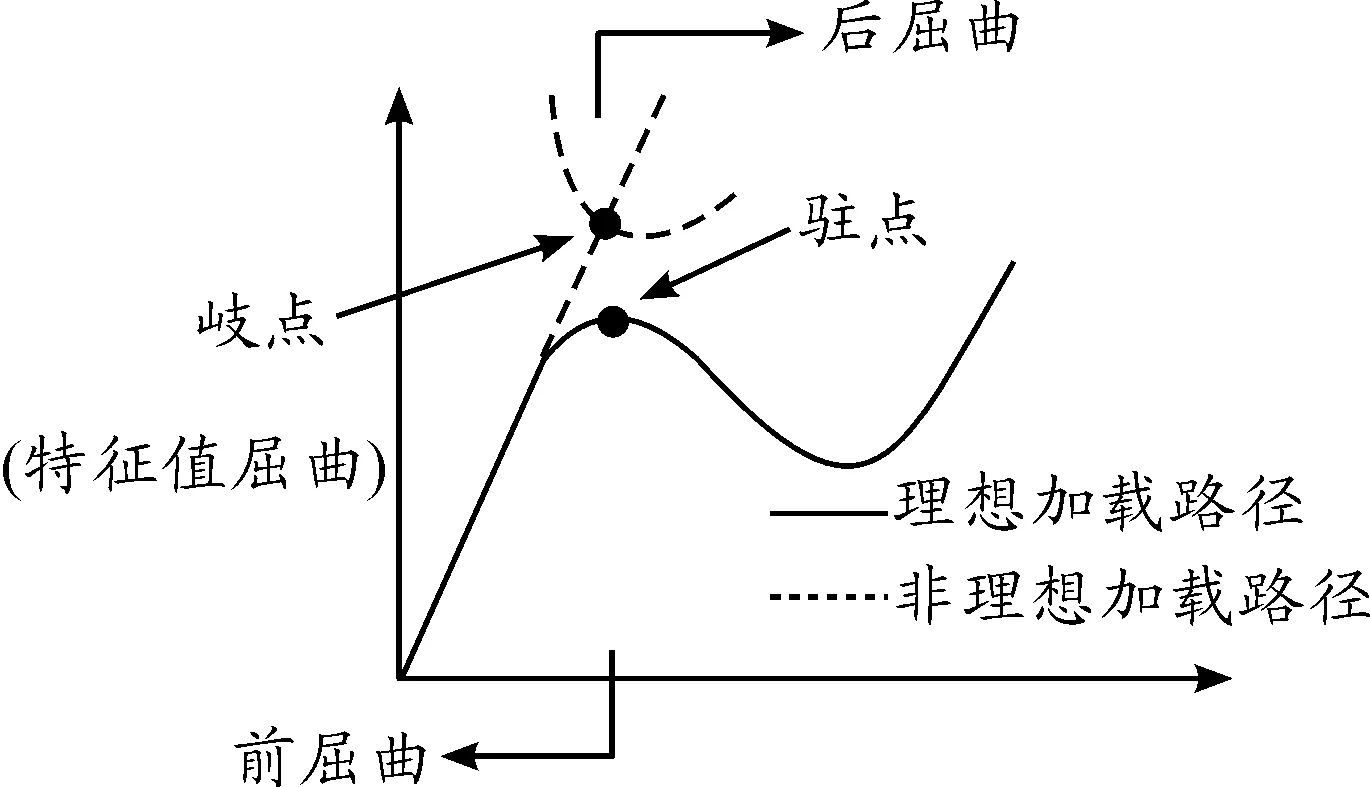
圖1 結構屈曲的載荷(F)-位移(u)示意圖

2 特征值屈曲

結構在外載荷作用下任意狀態時的增量平衡方程是

(1)

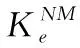
(2)

達到失穩狀態時，結構失去進一步抵抗變形的能力，此時應有ΔPN≈0，而增量平衡方程變為

(3)

因此，線性屈曲轉化為特征值問題。最小特征值λ代表了臨界載荷比例因子，特征向量ΔuM代表了失穩模態。

3 廣義弧長法求解非線性屈曲

非線性屈曲的求解一般采用廣義弧長法，即每一個增量步是弧長步而不是載荷步。在圖2所示的求解空間里，弧長法是借助一個弧面將載荷因子增量Δλ和位移增量ΔuN關聯起來。

其中，弧長由下式決定

(4)

圖2表示一個弧長步內的迭代求解過程；一個非線性問題的求解過程是由多個弧長步組成。

4 修正的Riks算法

4.1 初始載荷因子增量的求解

修正的Riks算法即修正的弧長法，其特點是用“平面”代替“弧面”，具有求解精度好、效率高等特點，為ABAQUS所采用。在多維求解空間里，修正的Riks法(Modified Riks algorithm)的求解過程如圖3所示。

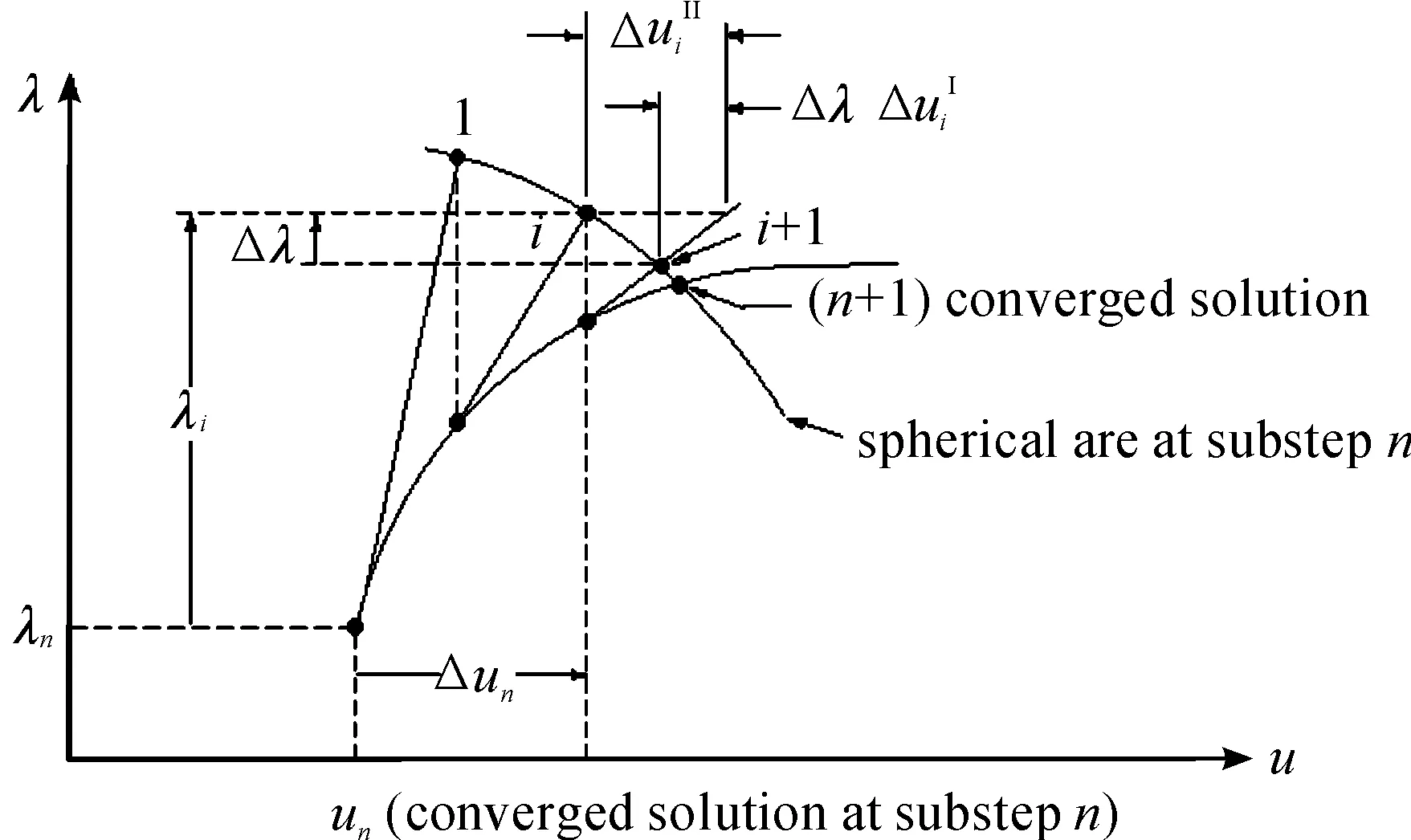
圖2 弧長法求解非線性屈曲

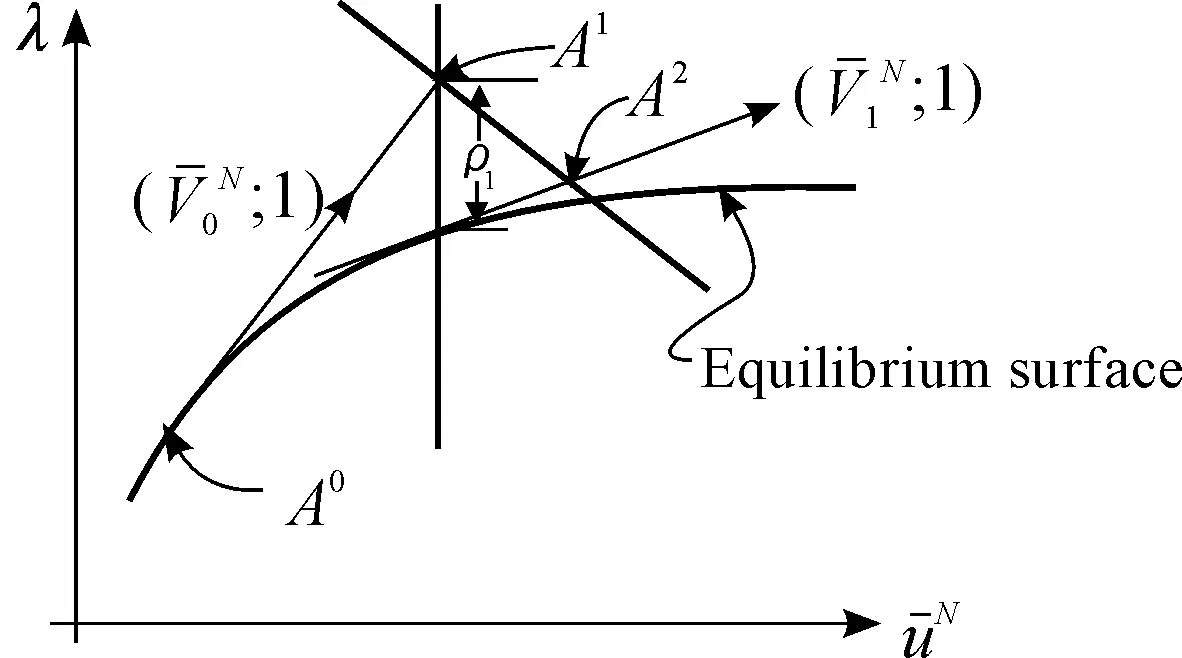
圖3 修正的Riks算法求解非線性屈曲

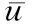
(5)

第一個弧長Δl的大小由用戶指定。則應有

(6)

(7)

從而

(8)

此處

(9)

求得Δλ0以后，開始進行如下過程的迭代。

載荷因子增量及位移增量初始化，有

Δλi=Δλ0

(10)

(11)

4.2 迭代過程

在第i個迭代步，形成節點應力矩陣IN，切線剛度矩陣KNM

(12)

(13)

其中βN是應變位移轉換矩陣。這樣，求解空間中的力和位移的預測點Ai所對應的狀態為

(14)

檢查迭代平衡

(15)

式(15)為解空間點Ai所對應的力和節點力產生的殘差力。若殘差力足夠小，達到收斂標準，則該弧長步的迭代收斂，下一個弧長步的迭代開始。若達不到收斂標準，則繼續迭代求解。

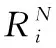
(16)

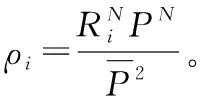
(17)

可求得：

(18)

這樣就確定了Ai+1的位置，其對應的狀態為

(19)

更新變量，返回到式(10)，準備下一個迭代：

(20)

Δλi+1=Δλi+μ

(21)

i=i+1

(22)

(23)

5 算例

長度L=600 mm，半徑R=300 mm，厚度t=2 mm，彈性模量E=70 000 MPa，泊松比μ=0.3的圓筒殼，底部簡支，自由端施加軸向壓力，分析軸壓穩定性。

5.1 根據工程計算公式求解

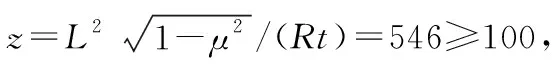
航天飛行器結構設計應用中，對大量圓柱殼體的軸壓穩定性試驗的數據進行統計，歸納出如圖4的設計曲線，即軸壓臨界應力系數k0～R/t曲線。根據圖4所示的曲線查取相應的k0，再根據公式σcr=k0Et/R進行計算。

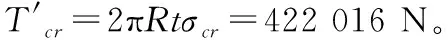
由圖4可以看出，根據設計曲線求得的臨界軸壓非常保守。

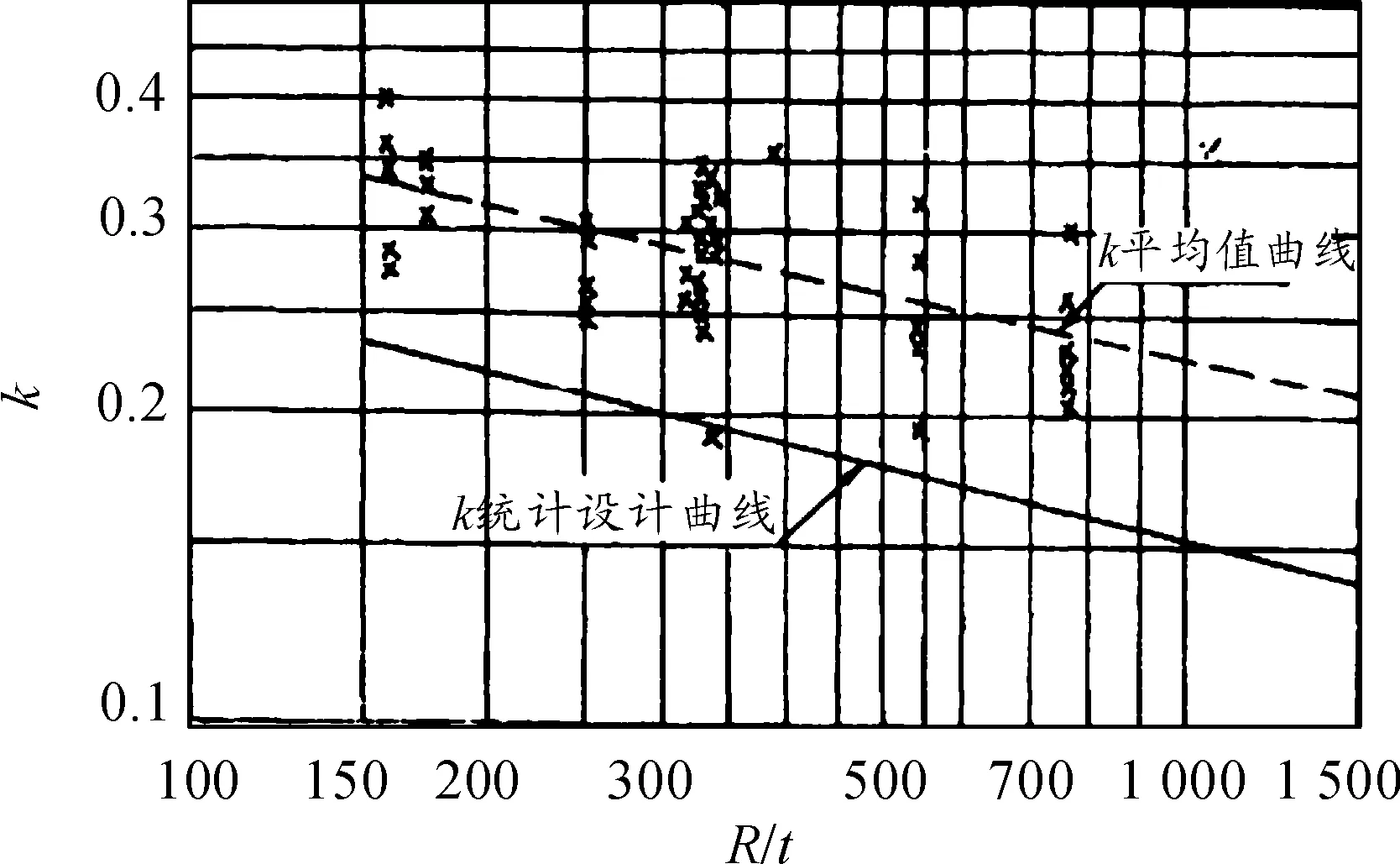
圖4 軸壓臨界應力系數k0～R/t曲線

5.2 有限元法

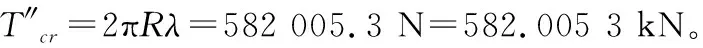
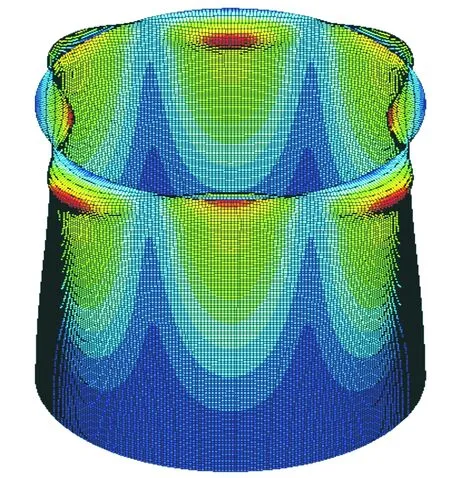
圖5 特征值屈曲模態

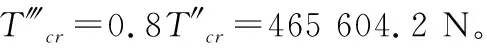
由計算分析看出，非線性屈曲的臨界應力T?明顯低于特征值屈曲求得的臨界應力T″，略高于經驗公式求得的臨界應力T′。非線性屈曲的臨界應力T?和經驗公式的臨界應力T′之比為T?/T′=1.1/1，二者比較接近。

改變圓筒殼的長度和厚度，同樣可以進行非線性屈曲的求解。幾種工況下有限元非線性屈曲分析求得的臨界軸壓和工程公式計算得到的臨界軸壓之比T?/T′如表1所示。由表1可見，有限元非線性屈曲的臨界軸壓計算結果和采用工程公式的計算結果吻合度較好。其中，t=3 mm時k0可取0.26。

圖6 非線性屈曲失穩變形

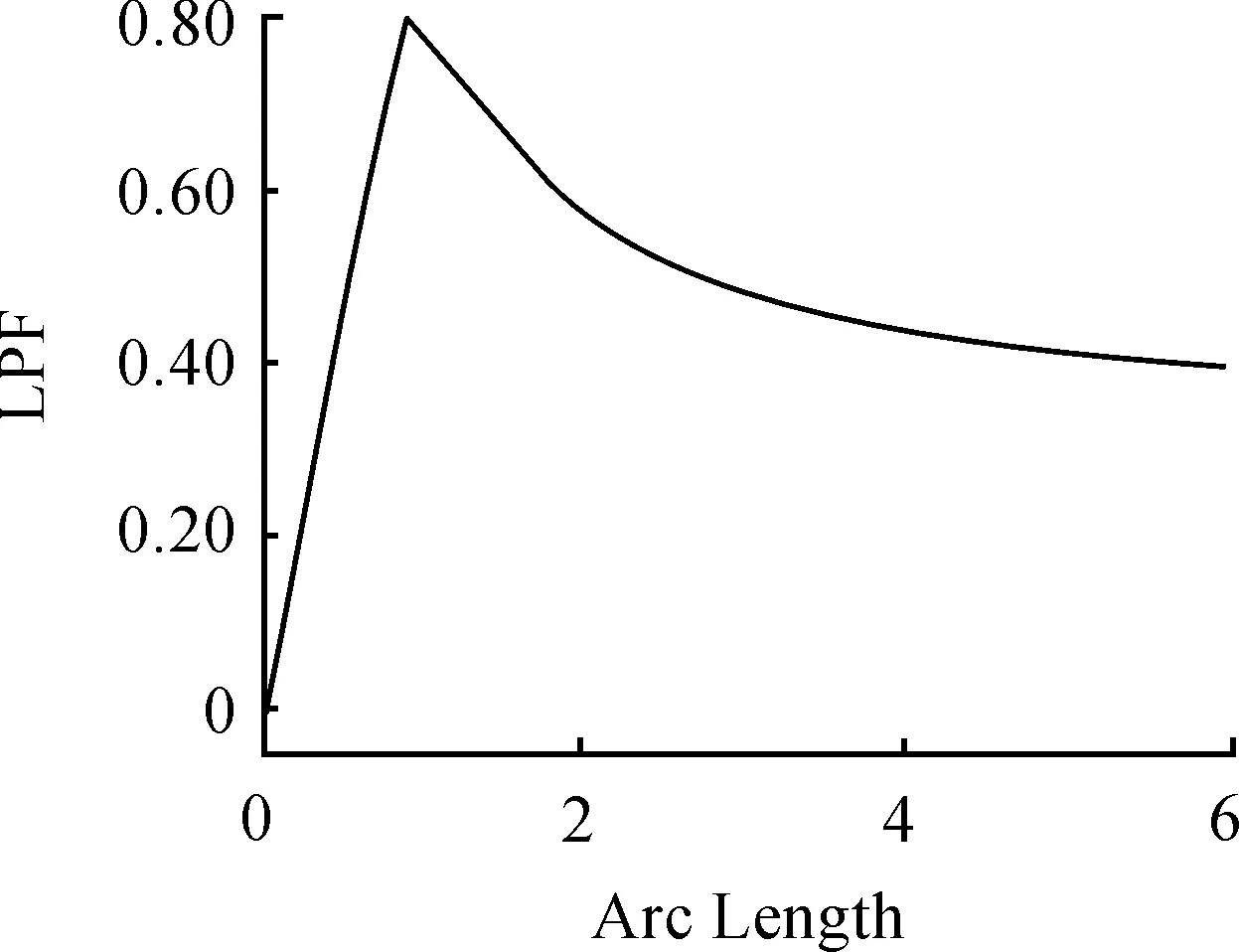
圖7 載荷比例因子和弧長的關系

L=600 mmL=900 mmL=1 200 mmt=2 mm1.1/11.1/11.05/1t=3 mm1.01/11.04/11.02/1

對應上述6種工況的線性特征值屈曲模態和非線性屈曲失穩變形圖如圖8～圖13所示。每個圖的左圖為線性屈曲模態示意圖，云圖為位移，右圖為非線性屈曲失穩示意圖，云圖為MISES應力。

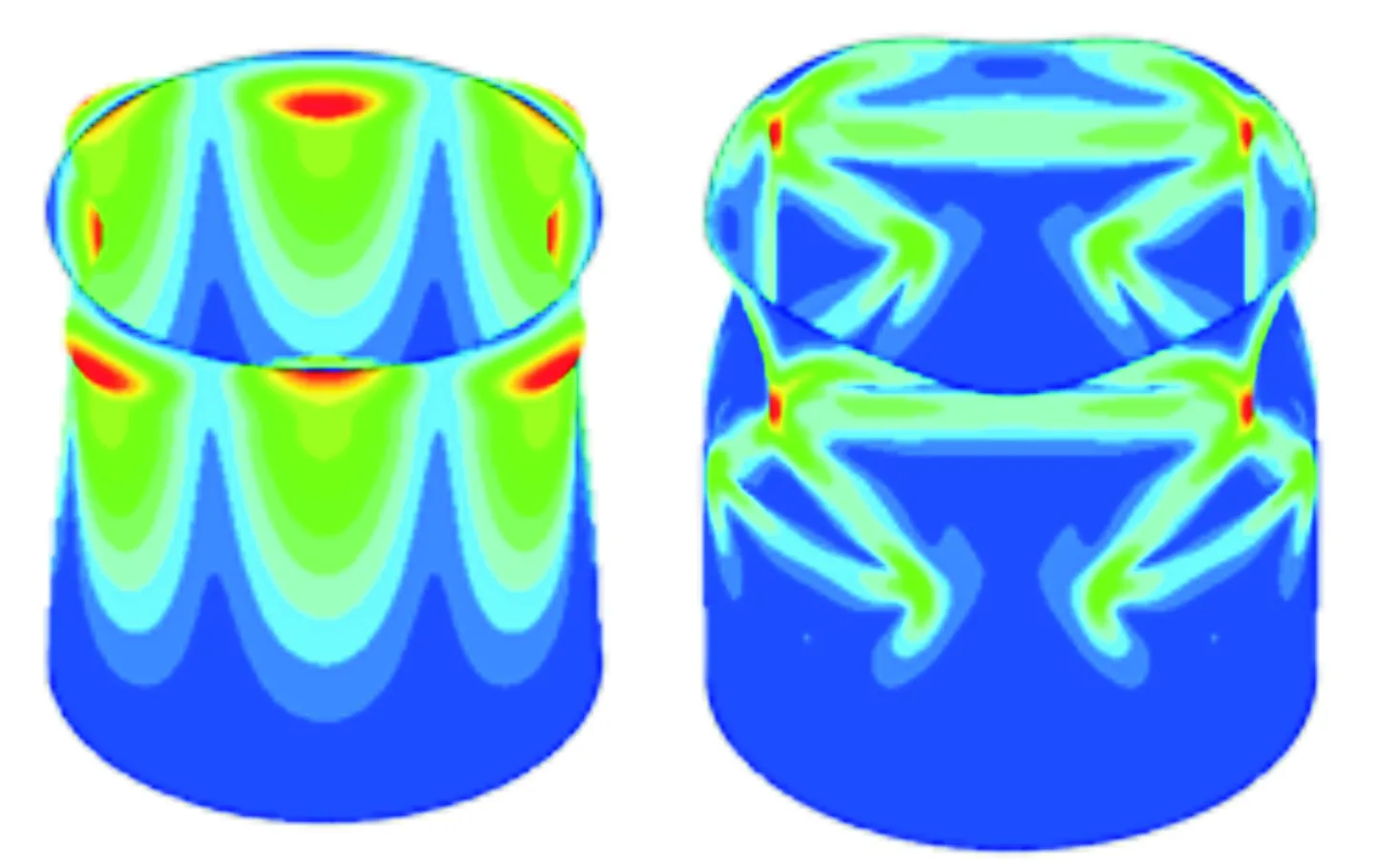
圖8 L=600 mm，t=2 mm時屈曲變形

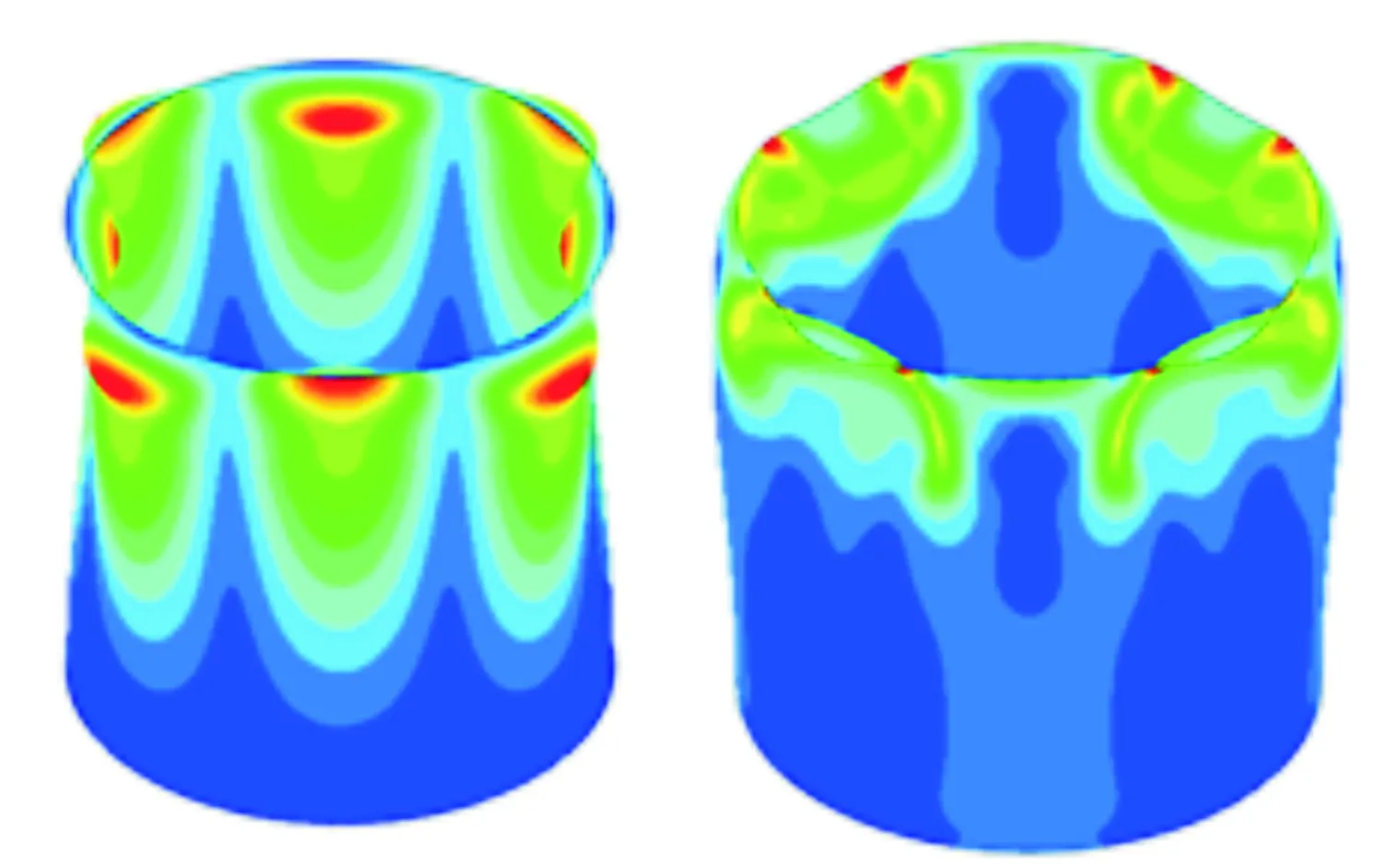
圖9 L=600 mm，t=3 mm時屈曲變形

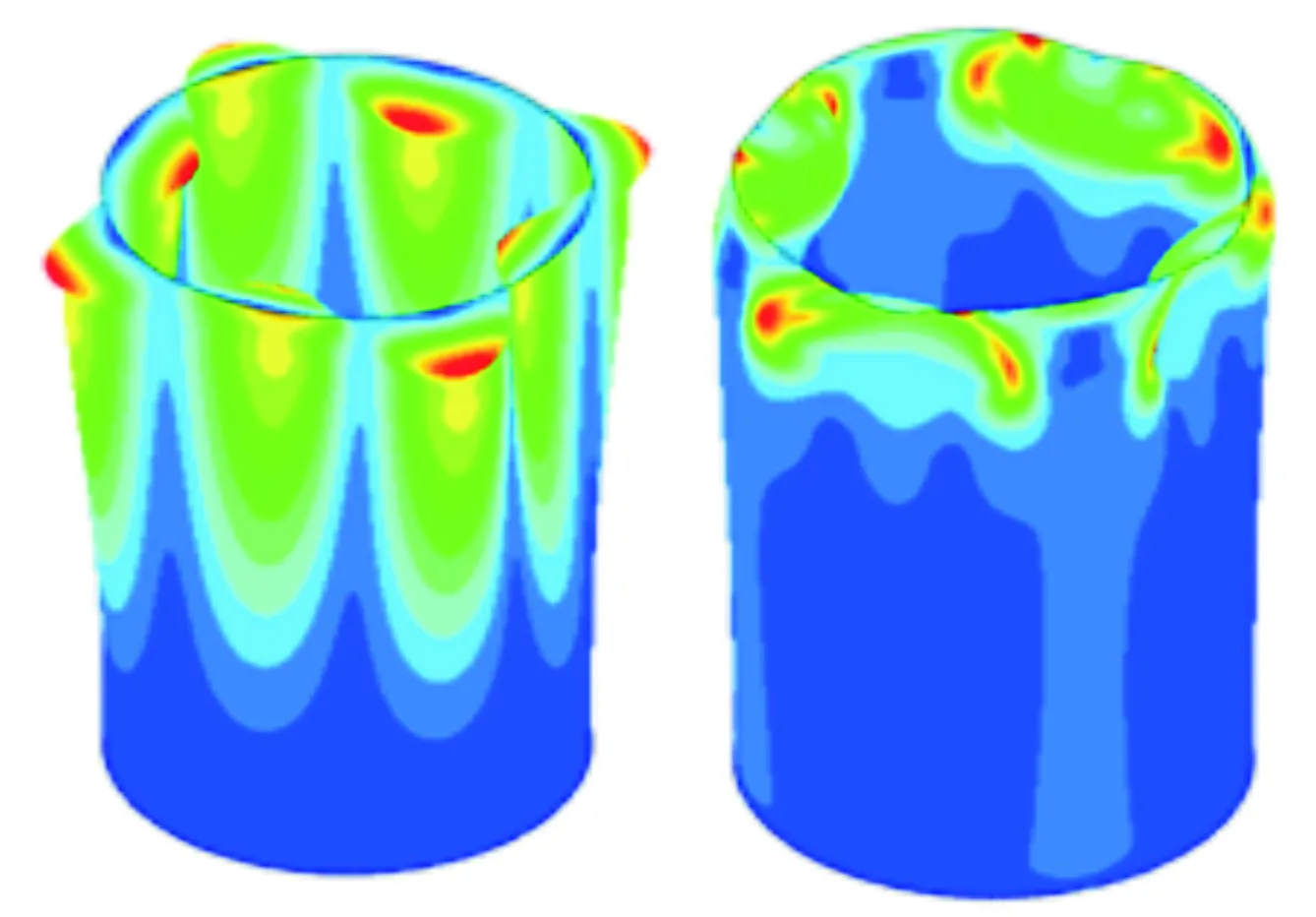
圖10 L=900 mm，t=2 mm時屈曲變形

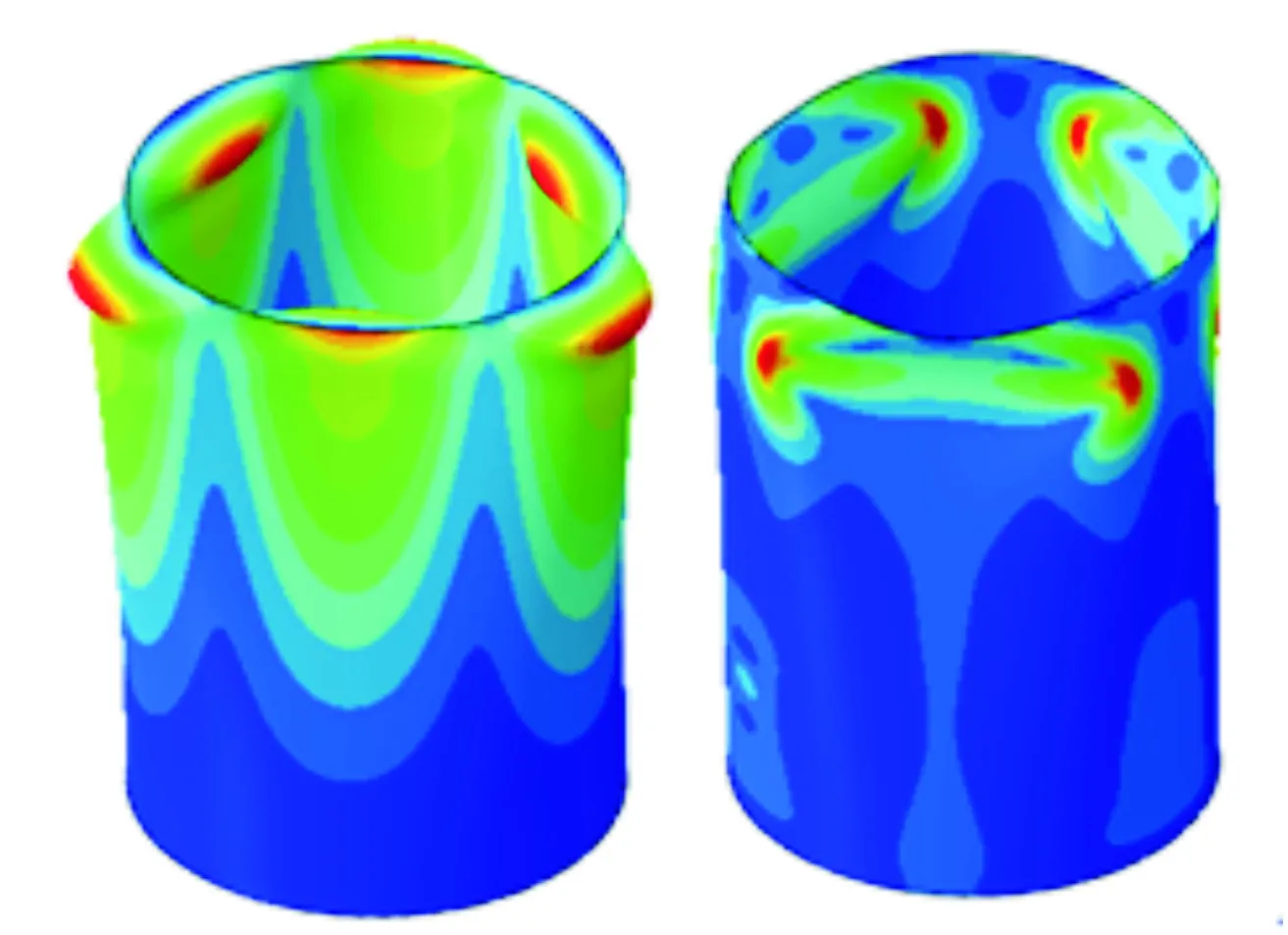
圖11 L=900 mm，t=3 mm時屈曲變形

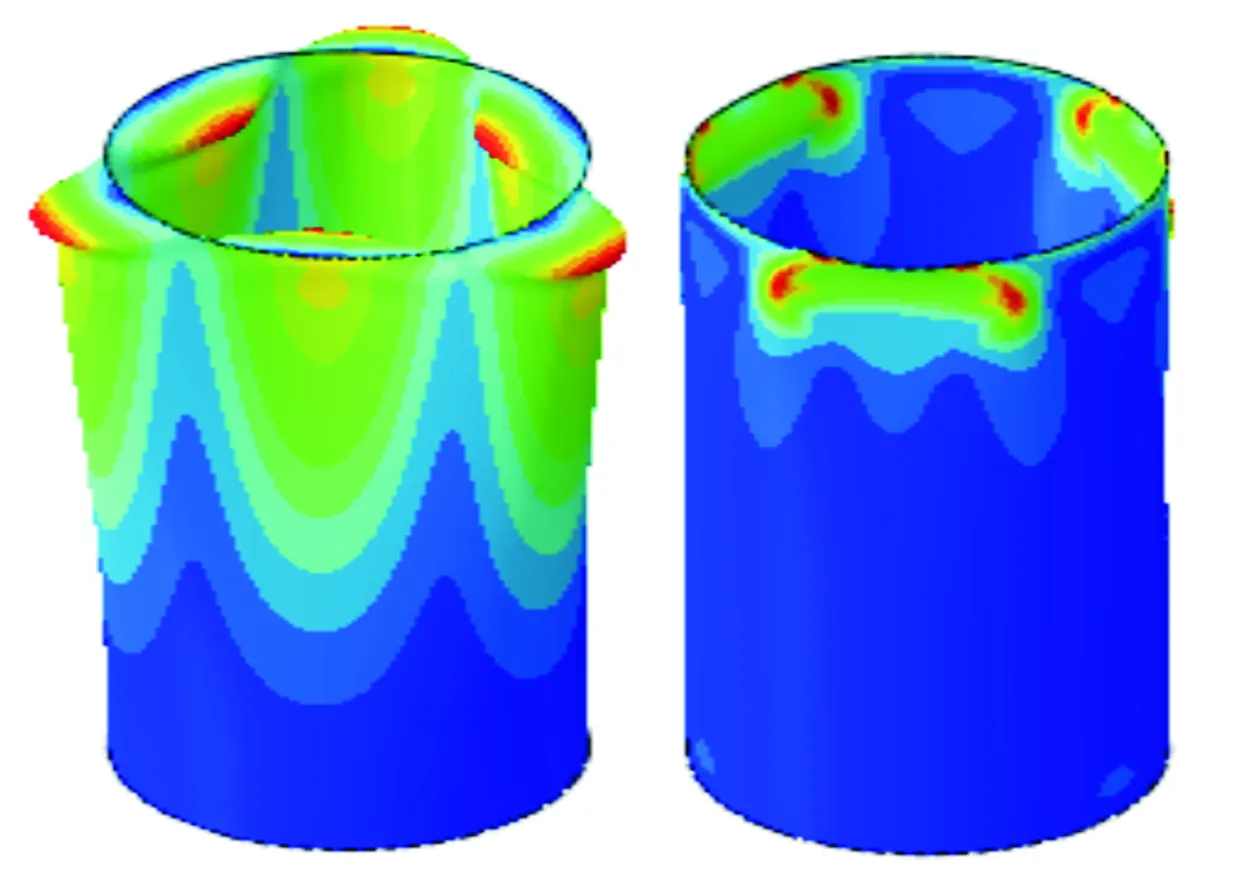
圖12 L=1 200 mm，t=2 mm時屈曲變形

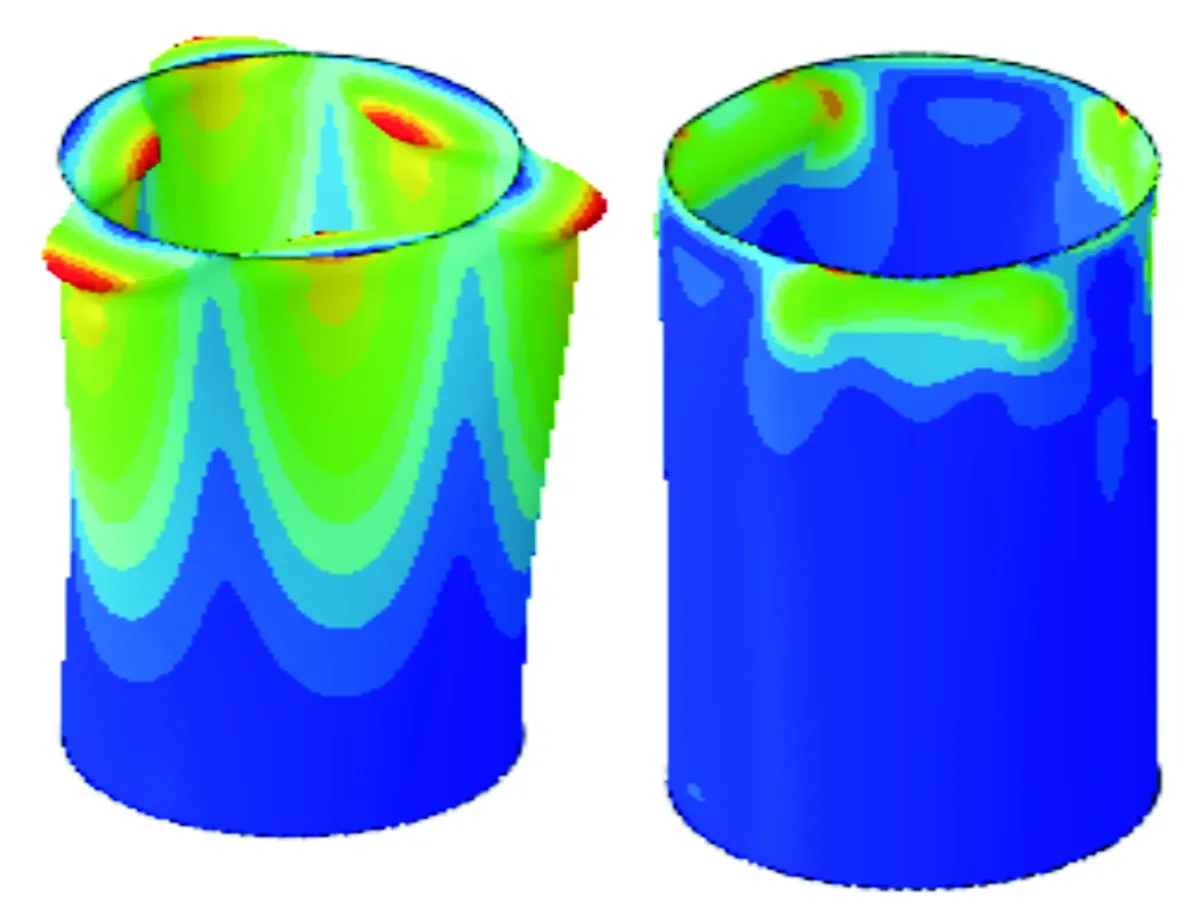
圖13 L=1 200 mm，t=3 mm時屈曲變形

6 結論

1) 采用特征值屈曲模態缺陷和修正的Riks算法，對薄壁圓筒進行了屈曲分析，并將分析結果和工程計算公式的分析結果進行了對比，二者具有一致性。

2) 有限元法對任意結構均能求解。對于無法用公式求得臨界軸壓的結構，采用基于特征值屈曲模態缺陷的弧長法進行非線性屈曲求解，可以得到合理的結果。

3) 采用特征值屈曲模態缺陷進行分析，不必事先知道缺陷的具體位置和缺陷的性質，在特征值屈曲的基礎上引入厚度的10%作為缺陷參數，采用弧長法進行非線性屈曲分析，可以滿足工程設計需要，尤其是在工程研制的方案階段，在沒有真實產品用來進行試驗的情況下，采用這種方法進行前瞻性的設計和分析，具有重要的意義。