一種基于自適應網格的PD雷達雜波譜仿真方法

劉廣君，吳元偉，王李波

(1.中國空空導彈研究院， 河南 洛陽 471009； 2.航空制導武器航空科技重點實驗室， 河南 洛陽 471009)

等距離線-多普勒線組成網格的雜波計算方法在20世紀60年代末形成[1-2]；1980年波音公司的Jao.J.K等提出了地平面下視條件下的網格積分的閉合解[3]；1990年，梁志恒等將這種方法引進國內的雜波計算中[4]。近些年，國內也出現一系列使用該方法進行雜波譜仿真的結果[5-7]。但是，這種網格劃分方法存在3個問題: ① 網格面積計算復雜。針對不同的9種情況，網格面積計算公式各不相同[4]，如果實時計算，復雜的計算占用大量時間，不能實現雜波的實時仿真。雖然可以將網格面積預先處理并存儲，但是針對不同的平臺運動和雷達指向，經過處理的網格面積仍然為近似值。② 該方法只有針對下視情況的公式推導。在目前情況下，在地面繞飛、超低空飛行等情況下，上視情況下雜波的影響不能忽略。③ 該方法未考慮同一個網格內天線增益和地面后向散射系數的變化，導致雜波譜計算精度低。在這種情況下，國內研究人員嘗試了等距離-等方位角[8]或者矩形網格[9]的方法避開網格面積計算復雜的問題。

本研究在考慮脈沖收發時序的情況下，基于自適應網格劃分方法，先利用脈沖收發時序將地面進行等距離-等方位角網格粗劃分，再利用網格特征參數對網格進行細劃分；之后根據坐標轉換得出面元對應的網格距離、網格面積、網格后向散射系數、網格天線增益、多普勒頻移等參數；最后利用統計方法得到雜波頻譜。

1 面雜波計算方法

1.1 雷達方程數字化

將雷達方程由積分形式變為差分形式[10]：

(1)

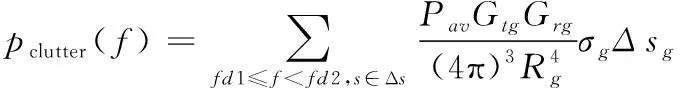
(2)

其中：pclutter、pt、λ、R分別為雜波功率、發射功率、雷達波長、面元-雷達距離；Gr、Gt為天線接收和發射增益；σ、ds分別為面元后向散射系數和面元面積，L為空間衰減；下標‘g’表示前述參數的網格單元值。

通過分別計算R、σ、ds、Gr、Gt來計算接收的雜波功率；通過對符合條件的面元的反射功率進行求和得到雜波功率譜。

面元-雷達距離和面元面積在網格劃分中得到，天線接收、發射增益和面元后向散射系數通過坐標轉換和天線方向圖、地面后向散射系數得到。

1.2 自適應網格劃分方法

為簡化計算，將發射脈沖視為點脈沖信號，地面網格回波在脈沖收發時序的位置可以簡單地用雷達-地面網格距離表示。

自適應雜波面元網格劃分分為兩個步驟：基于等距離-等方位角的初步網格劃分和基于網格特征點增益差異的網格加密。

首先，根據雷達的脈沖重復周期和各個接收門在脈沖重復周期內的位置，將地面劃分為一個個等距離環；同時，根據等方位角，將一個等距離環劃分為等大小的扇形區域。距離向對應著發射-接收距離門，故按照距離分辨率劃分。考慮到接收距離門在整個脈沖時序中的位置，距離向網格劃分中，只對接收門對應地面距離區間進行劃分(如圖1所示)。如果是中重頻，只對關心的接收距離門進行網格劃分。方位向網格按照方位角均勻劃分，圖2為網絡加密示意圖。

其次，判斷扇形區域的特征點參數的差異ΔGg(天線增益和地面后向散射系數)，如差異過閾值則將網格劃分為4份；重復此步驟直至扇形區域的特征點參數無明顯差異。

Gg=Gtg+Grg+σg

(3)

ΔGg=max(Gg)A,B,C,D,E-min(Gg)A,B,C,D,E

(4)

其中，Gtg、Grg、σg分別為網格點的天線發射增益、天線接收增益、地面后向散射系數。

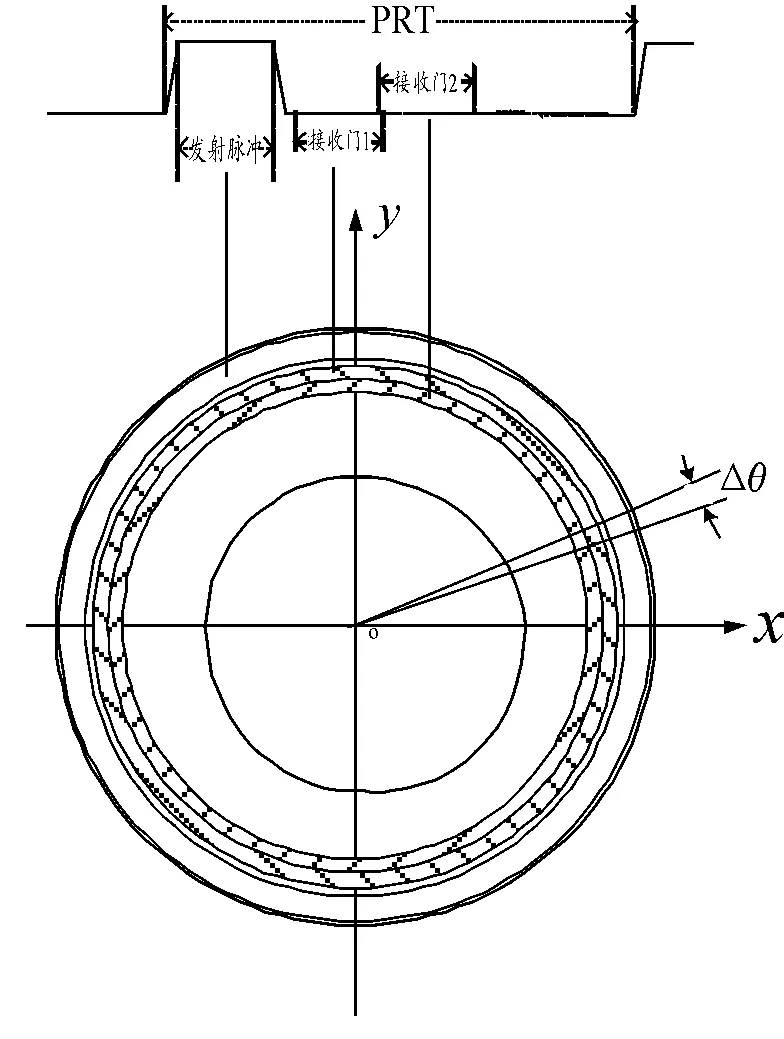
圖1 脈沖收發時序示意圖

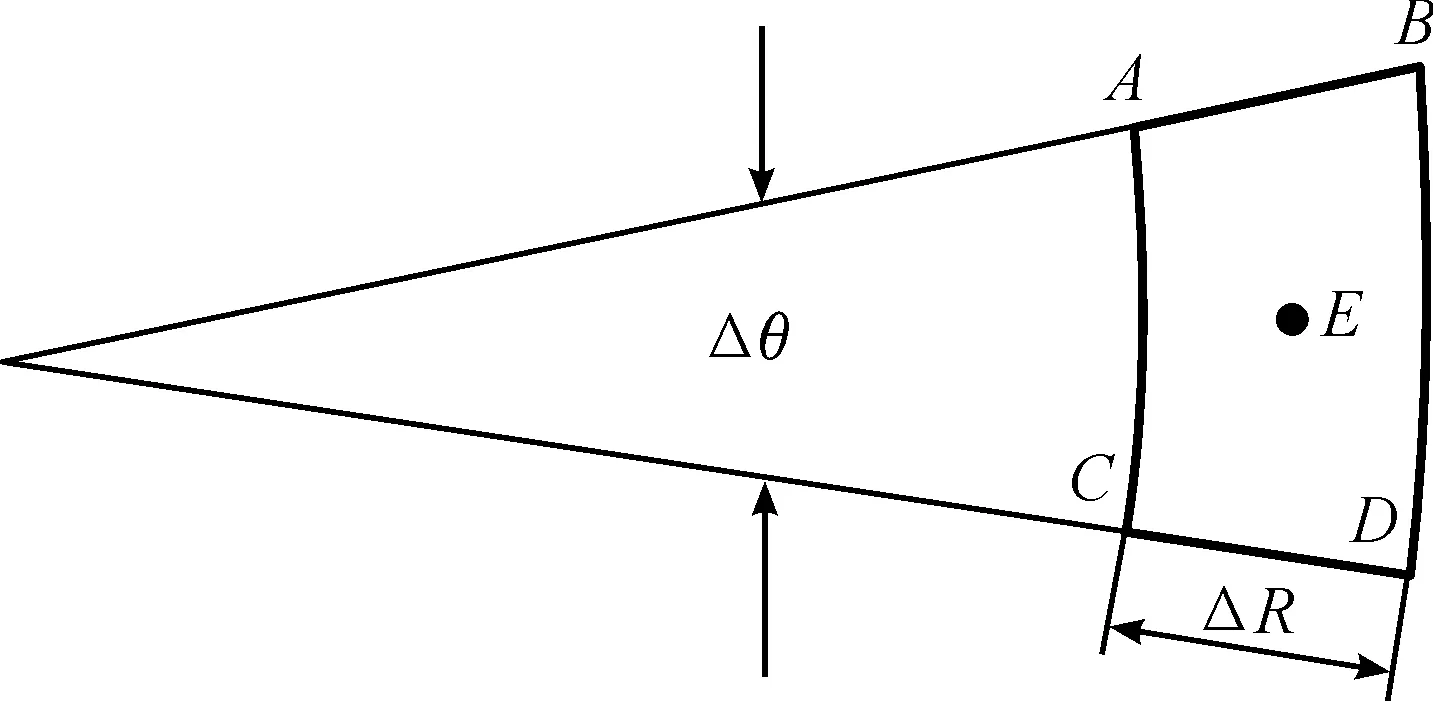
圖2 網格加密示意圖

1.3 雜波計算中的坐標轉換

雜波計算中，雷達平臺運動方向、夾具指向、天線指向的關系如圖3所示。

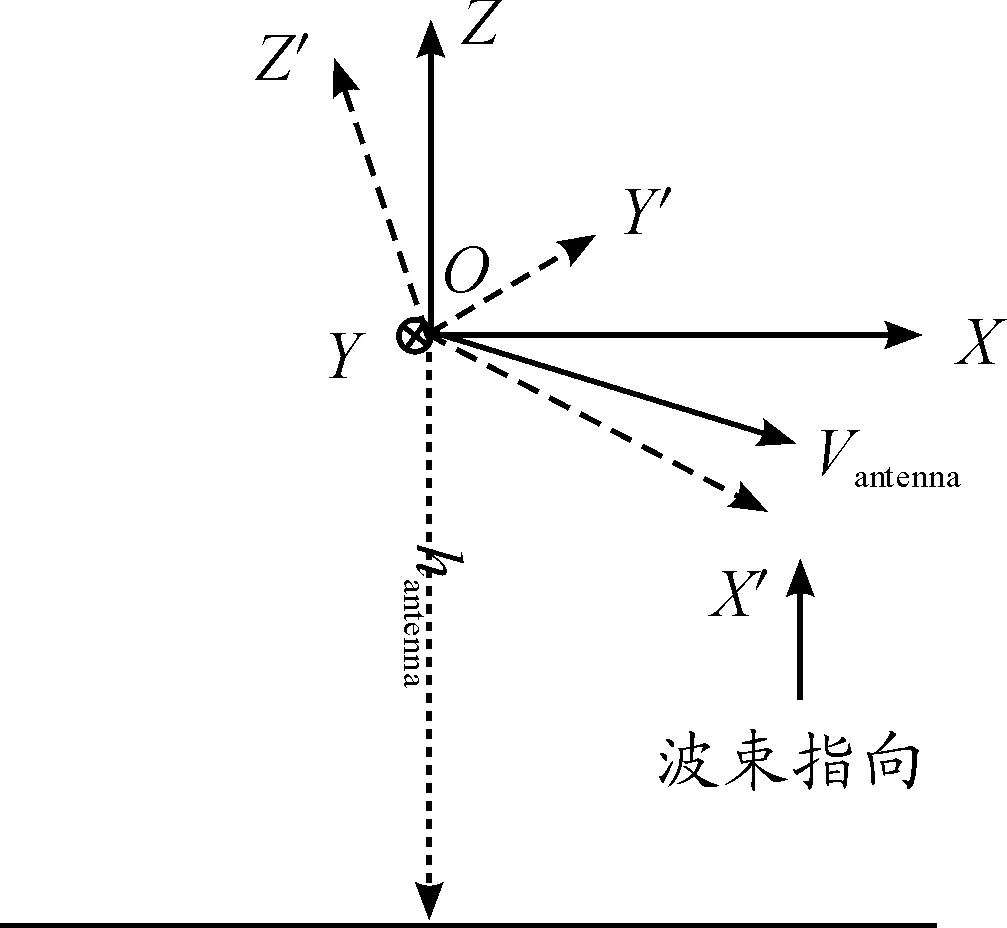
圖3 雷達平臺運動方向、夾具指向、天線指向關系

以雷達中心為原點建立慣性坐標系。慣性坐標系中，向上為z軸正向；在飛機速度方向和z軸確定的平面內、水平且和飛機速度夾角小于90°的方向為x軸，x、y、z成右手系。

假設地球半徑為Re，Rg為面元-雷達距離，雷達高度為h，Re≥Rg條件下，面元在慣性系中的坐標為(xg,yg,-hantenna)。

如果知道天線指向在慣性坐標系中的擦地角θ和方位角φ，就可以直接計算地面網格在天線坐標系中的位置，轉換坐標的方法如下：

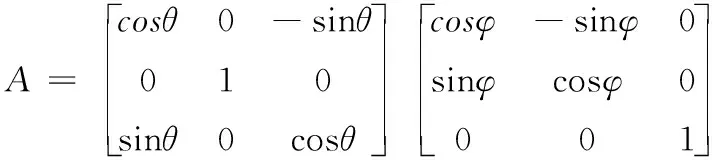
(5)

(6)

[φnew,θnew,rnew]=cart2sph(yg_antenna,zg_antenna,xg_antenna)

(7)

φnew、θnew分別為地面網格在天線坐標系中的方位角、和天線正前方的夾角。

1.4 網格參數計算

由1.3節得到φnew、θnew，結合三維天線方向圖即可得到網格的天線收發增益。

由于地面后向散射系數僅和擦地角和地貌相關，網格擦地角θg計算如下：

(8)

通過網格擦地角和地面后向散射系數隨擦地角變化的數據即可得到網格地面后向散射系數。

在等距離-等方位角網格劃分方法中，網格面積dsg的表達式為：

dsg=2RgΔR/Nφ

(9)

其中：Rg為面元-雷達距離；ΔR為距離向網格寬度；Nφ為方位向網格劃分份數。

網格多普勒頻移fd和雷達平臺速度大小、網格-雷達矢量和雷達平臺速度Vantenna方向夾角相關。

(10)

(11)

其中：c為光速；f為雷達頻率；fd為網格多普勒頻移。

1.5 雜波譜仿真

將網格參數的數據代入雷達方程，可以得到每個網格單元的雜波回波強度；再通過網格多普勒頻移，可以得到雜波的功率譜。仿真流程如圖4所示。

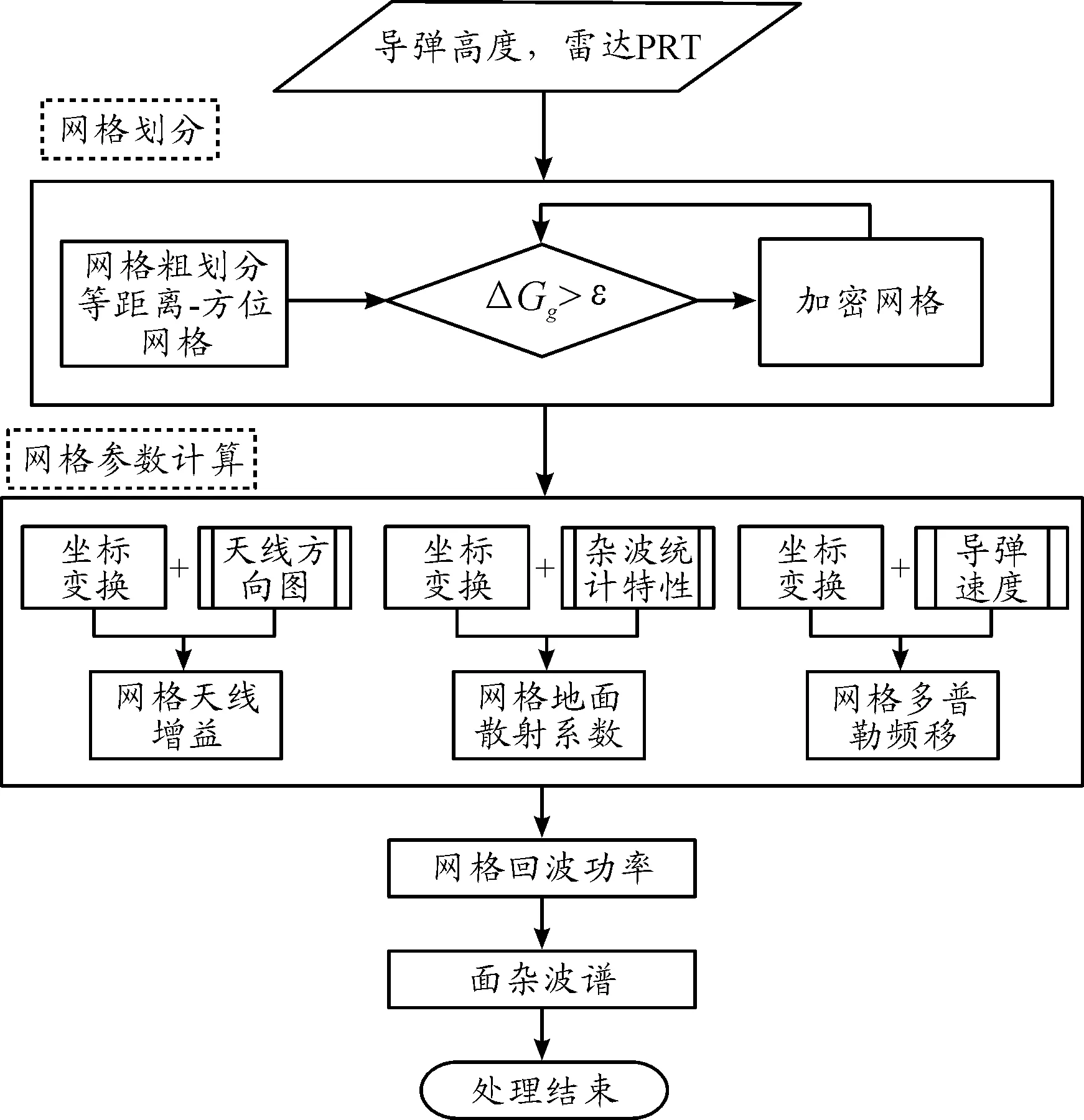
圖4 雜波仿真流程

2 雜波仿真結果

2.1 高重頻雜波仿真

高重頻雜波仿真條件如表1所示。

表1 高重頻仿真條件

得到雜波譜如圖5、圖6所示。隨著天線增益、雷達-地面相對姿態、地面后向散射系數的不同，雜波譜分為高度線雜波區域、旁瓣雜波區域，主雜波區域。且上視狀態下旁瓣雜波強度和下視狀態下旁瓣雜波強度基本相當，不能忽略。

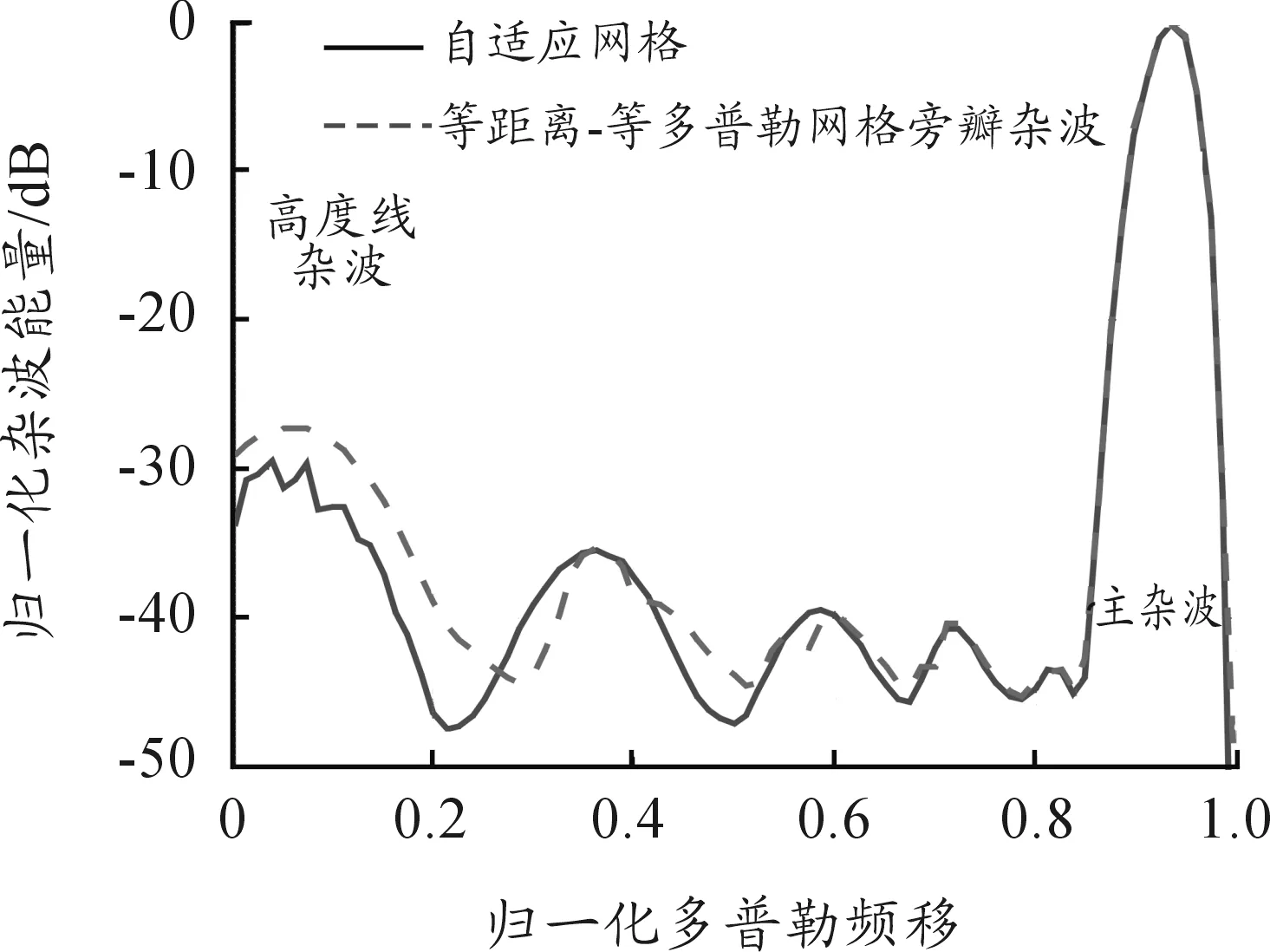
圖5 高重頻下視雜波譜

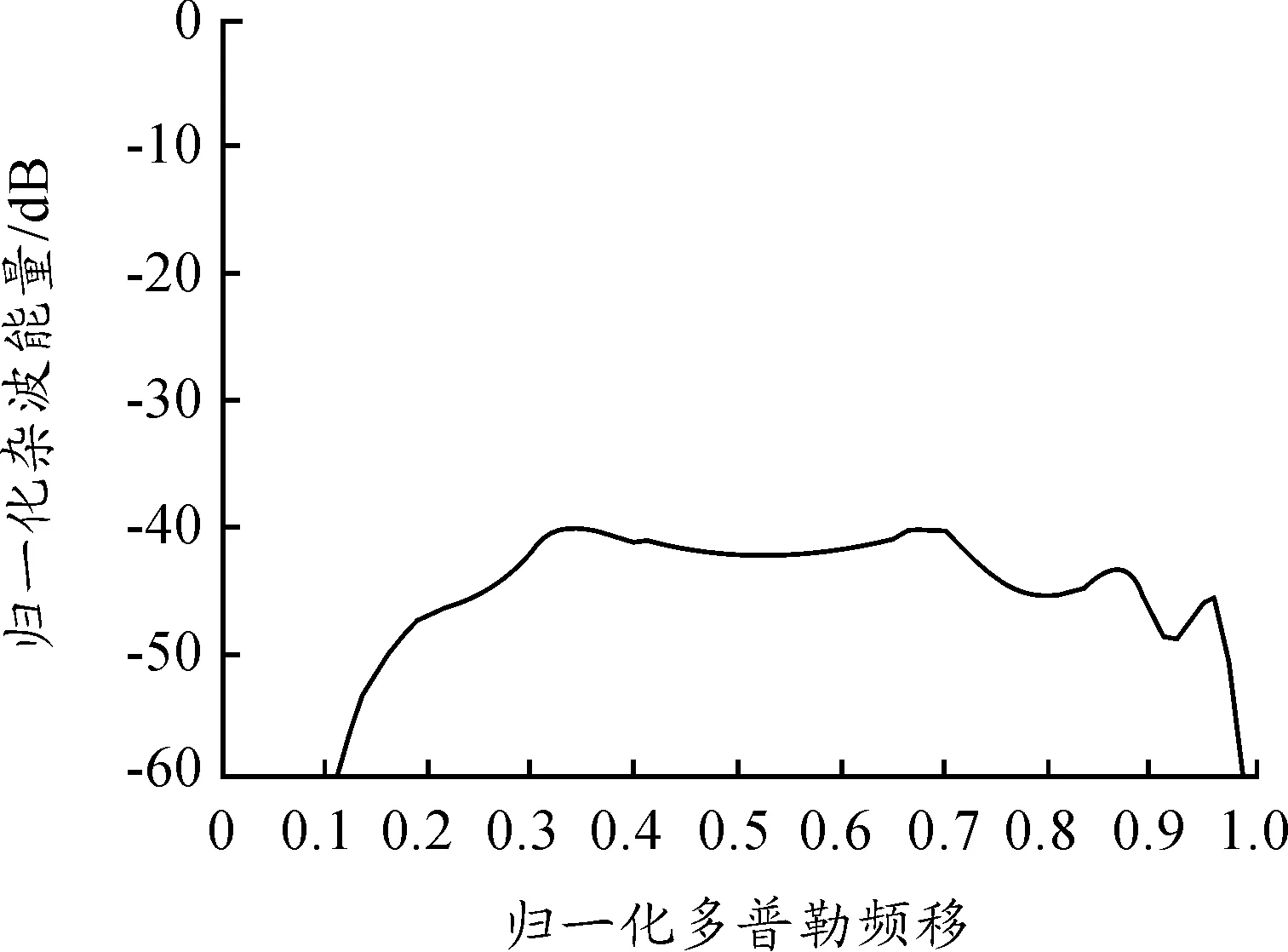
圖6 高重頻上視雜波譜

圖5展示了表1中高重頻下視條件下，基于自適應網格的仿真結果、基于等距離-等多普勒網格的仿真結果。基于等距離-等多普勒網格的仿真耗時309.4 s，網格面積計算花費了大部分計算時間；基于自適應網格的仿真耗時8.3 s，運行速度提高37倍。從結果對比上看，二者在主雜波區和近旁瓣雜波取差別小于1 dB；在中旁瓣雜波區差別約3 dB；在遠旁瓣雜波區和高度線雜波區差別約5 dB。

2.2 中重頻雜波仿真

中重頻雜波仿真條件如表2所示。

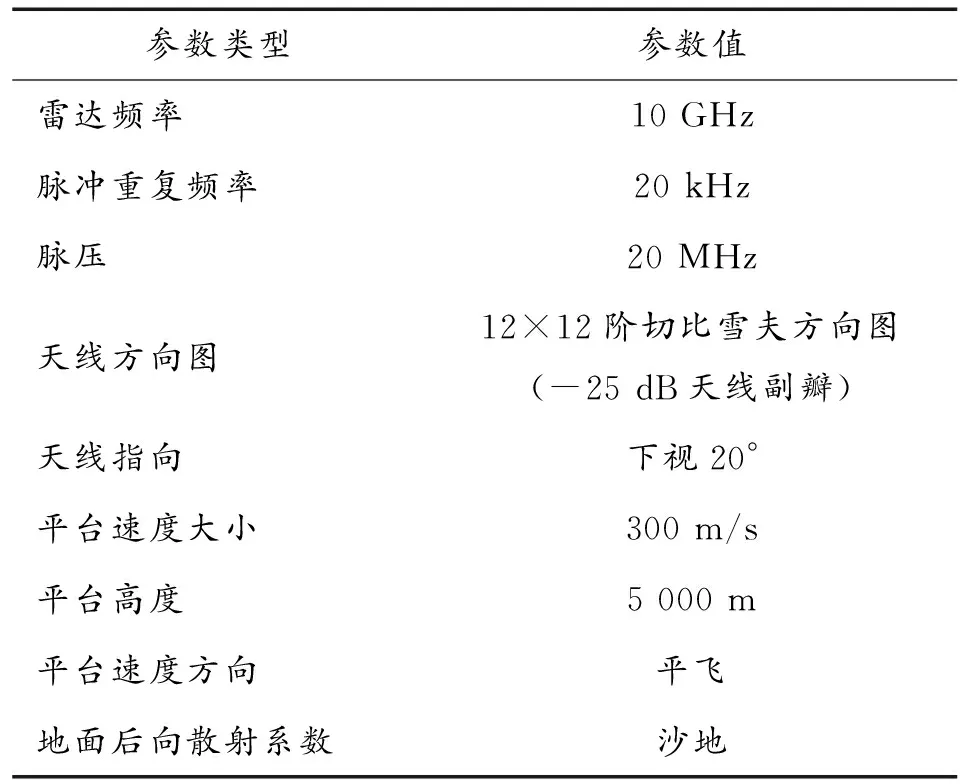
表2 中重頻仿真條件

得到雜波譜如圖7所示。隨著天線增益、雷達-地面相對姿態、地面后向散射系數的不同，雜波譜分為高度線雜波區域、旁瓣雜波區域，主雜波區域。

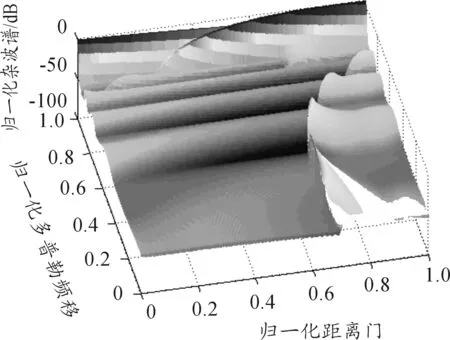
圖7 中重頻頻域雜波譜

3 結論

1) 本研究提出了一種基于坐標變換、等距離-等方位角的脈沖多普勒雷達地面雜波時頻域仿真方法。

2) 本方法避免了等距離-等多普勒劃分方法中復雜的面積計算，可以處理雷達上視、平視、下視情況下的雜波仿真。通過本方法得到的雜波信號，和經典算法基本一致，計算效率大大提高。