初始誤差和制導工具誤差的線性估計方法

李 冬,龔 磊

(中國人民解放軍92124部隊， 遼寧 大連 116023)

制導工具誤差是引起飛行器落點偏差的重要因素之一，飛行器精度評定通常將特殊軌跡分離出的制導工具誤差折算到最大射程軌跡上，進而獲得全程軌跡的落點精度[1-2]。與固定發射飛行器相比，動基座發射飛行器落點精度還會受到慣導系統初始定位誤差、調平對準誤差和初速測量誤差的影響，這些初始誤差與制導工具誤差耦合在一起，共同引起落點偏差。有研究表明，初始誤差帶來的落點偏差在量級上與制導工具誤差相當[3]。如何準確分離初始誤差和制導工具誤差是動基座發射飛行器精度評定亟需解決的重要問題。

許多學者開展了動基座發射飛行器誤差分離方法的研究。文獻[4]通過分析初始誤差對遙外差數據的影響，建立了估計初始誤差的線性模型，但沒有估計制導工具誤差。鄭小兵等[5]利用地面測試數據減小制導工具誤差對遙外差的影響，在此基礎上給出了一種利用飛行起始段的遙外差數據估算初始定位誤差的方法。張仲毅等[6]在分離初始誤差的線性模型中將定向誤差歸算為射擊方位角誤差和平臺初始失準角。胡正東等[7]建立了同時估計初始誤差和制導工具誤差的線性模型，楊華波等[8]通過仿真實驗對該模型的正確性進行了驗證，但實驗中考慮的制導工具誤差項數較少，當制導工具誤差中包含加速度計安裝誤差角時，該模型存在復共線性，無法給出誤差的準確估計值。

本文針對動基座發射飛行器的初始誤差和制導工具誤差的估計問題，分析了定向誤差與平臺初始失準角的轉換關系，采用線性化近似方法建立了同時估計初始誤差和制導工具誤差的線性模型，在此基礎上給出了誤差估計的Bayes方法，解決了線性模型的復共線性，通過仿真實驗檢驗了誤差估計的精度。

1 估計初始誤差和制導工具誤差的線性模型

動基座發射飛行器的制導控制需要慣導系統提供發射時刻的導航參數，這些參數包括定位參數(發射點的大地緯度B0、大地經度L0、大地高程H0)、定向參數(發射點的天文緯度BT、天文經度LT、天文射擊方位角AT)和初始速度參數V0=(vx0,vy0,vz0)T。把慣導系統的測量誤差以及調平對準誤差帶來的導航參數誤差稱為初始誤差，包括定位誤差(ΔB、ΔL、ΔH)、定向誤差(ΔBT、ΔLT、ΔAT)和初速誤差ΔV=(Δvx,Δvy,Δvz)T。本文需定義理論發射系、理論發射慣性系、真發射系、真發射慣性系、平臺坐標系等坐標系統。理論發射系是以導航定位參數(B0,L0,H0)確定原點并以導航定向參數(BT,LT,AT)確定3個坐標軸指向的發射系，真發射系是以真實定位參數(B0+ΔB,L0+ΔL,H0+ΔH)確定原點以真實定向參數(BT+ΔBT,LT+ΔLT,AT+ΔAT)確定坐標軸指向的發射系。在發射零時刻，與理論發射系重合的發射慣性系稱為理論發射慣性系，與真發射系重合的發射慣性系稱為真發射慣性系。平臺坐標系的原點取為真發射慣性系的原點，坐標軸與3個陀螺儀的敏感軸平行。

1.1 平臺初始失準角與定向誤差的轉換關系

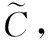
上式左右兩邊分別作關于(ΔBT,ΔLT,ΔAT)和(εpx,εpy,εpz)的泰勒展開，只保留一階項，可得平臺初始失準角與初始誤差的轉換關系式為

εp≈Γξ

(1)

其中

(2)

1.2 線性模型的建立

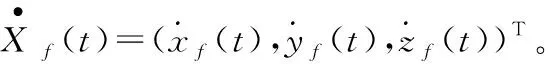
(3)

式(3)中：Φ(t)為理論發射系到理論發射慣性系的旋轉矩陣，Φ(t)=C-1Ω(t)C，Ω(t)=Rz(-ωt)，ω為地球自轉角速度，R0=C-1X0，X0為理論發射系原點的地心直角坐標

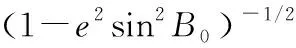
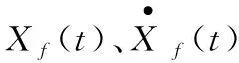
(4)

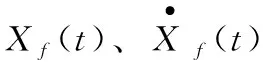
飛行器慣導平臺輸出的遙測數據為平臺坐標系下的視速度測量Wp(t)=(wpx(t),wpy(t),wpz(t))T，對其積分后可得平臺坐標系下的視位置數據Pp(t)=(ppx(t),ppy(t),ppz(t))T。Wp(t)、Pp(t)與Wr(t)、Pr(t)的偏差由制導工具誤差引起的，滿足如下關系[10]：

(5)

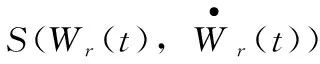
綜合式(4)和式(5)可得：

設采樣時刻為t1,t2,…,tn，令

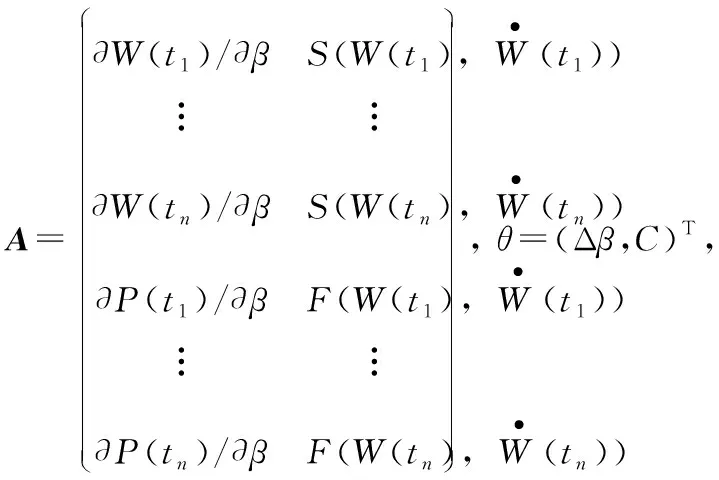
Y=Aθ+δ

(6)

在此稱A為環境函數矩陣。

1.3 環境函數矩陣的復共線性

將W(t)=(wx(t),wy(t),wz(t))T簡記為W=(wx,wy,wz)T，制導工具誤差中的平臺初始失準角εp=(εpx,εpy,εpz)T對應的視速度環境函數[10]為

(7)

定向誤差ξ=(ΔBT,ΔLT,ΔAT)T對應的視速度環境函數矩陣記為Sξ(t)，εp和ξ引起的視速度偏差是相同的，于是有

Sξ(t)ξ=Sε(t)εp

(8)

由式(1)和式(8)可得

Sξ(t)≈Sε(t)Γ

(9)

加速度計安裝誤差角α=(αxz,αxy,αyx,αyz,αzx,αzy)T[11]對應的視速度環境函數記為Sα(t)，有

(10)

由式(2)、式(7)、式(9)和式(10)可得

Sξ(t)≈Sα(t)H

其中

于是Sξ(t)和Sα(t)的列近似線性相關。同理可推導，ξ和α的視位置環境函數具有相同的線性關系。這樣，環境函數矩陣A關于ξ和α的列近似線性相關，具有很強的復共線性。而ξ和α對飛行器落點偏差的影響較大，不可忽略。

2 Bayes估計方法

對于模型式(6)，由于環境函數矩陣A關于ξ和α的列存在線性相關性，在沒有θ任何先驗信息的條件下無法唯一確定θ的估計值。在飛行器試驗前，通過地面測試得到制導工具誤差的先驗信息，這樣利用能夠融入先驗信息的Bayes極大后驗估計[12]可以獲得θ的最優估計，從而克服環境函數矩陣的復共線性。

假設模型(6)中誤差δ服從均值為零協方差矩陣為Pδ的高斯分布，且θ的先驗分布服從均值為θ0協方差矩陣為Pθ的高斯分布，則θ的Bayes極大后驗估計為

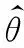
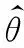
Pp(t)≈Φ(t)Px(t)Φ(t)T

δw(t)的協方差矩陣Pw(t)為

其中，

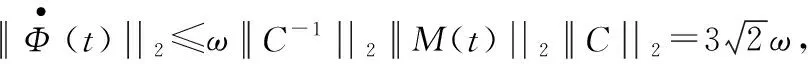
18ω2||Px(t)||2

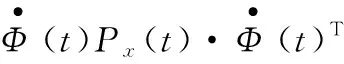
Pw(t)≈Φ(t)Pv(t)Φ(t)T

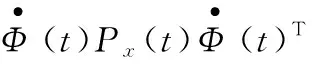
Pδ≈diag((Pw(t1),…,Pw(tn),Pp(t1),…,Pp(tn))

3 仿真實驗與結果分析

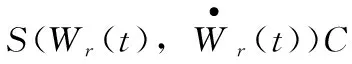
誤差比定義為：|估計值-真值|/真值，以誤差比小于等于0.4作為判斷估計好項的標準。表1給出了1 000次MC實驗制導工具誤差估計的平均誤差比，可以看出，Bayes估計方法有18個估計好的項，而主成分方法只有7個估計好的項。1 000次MC實驗初始誤差估計的均方根誤差如表2所示，可以看出，PCE方法對定向誤差的估計精度遠低于Bayes估計方法，PCE方法和Bayes估計方法對定位誤差和初速誤差的估計精度都很高，將初始定位誤差換算成距離度量單位，它們對定位誤差的估計精度分別為0.162 m和0.115 m。環境函數矩陣的復共線性導致PCE方法難以估準定向誤差，同時降低了制導工具誤差的估計精度，而Bayes方法利用了先驗信息，克服了環境函數矩陣的復共線性，估計結果的精度較高。

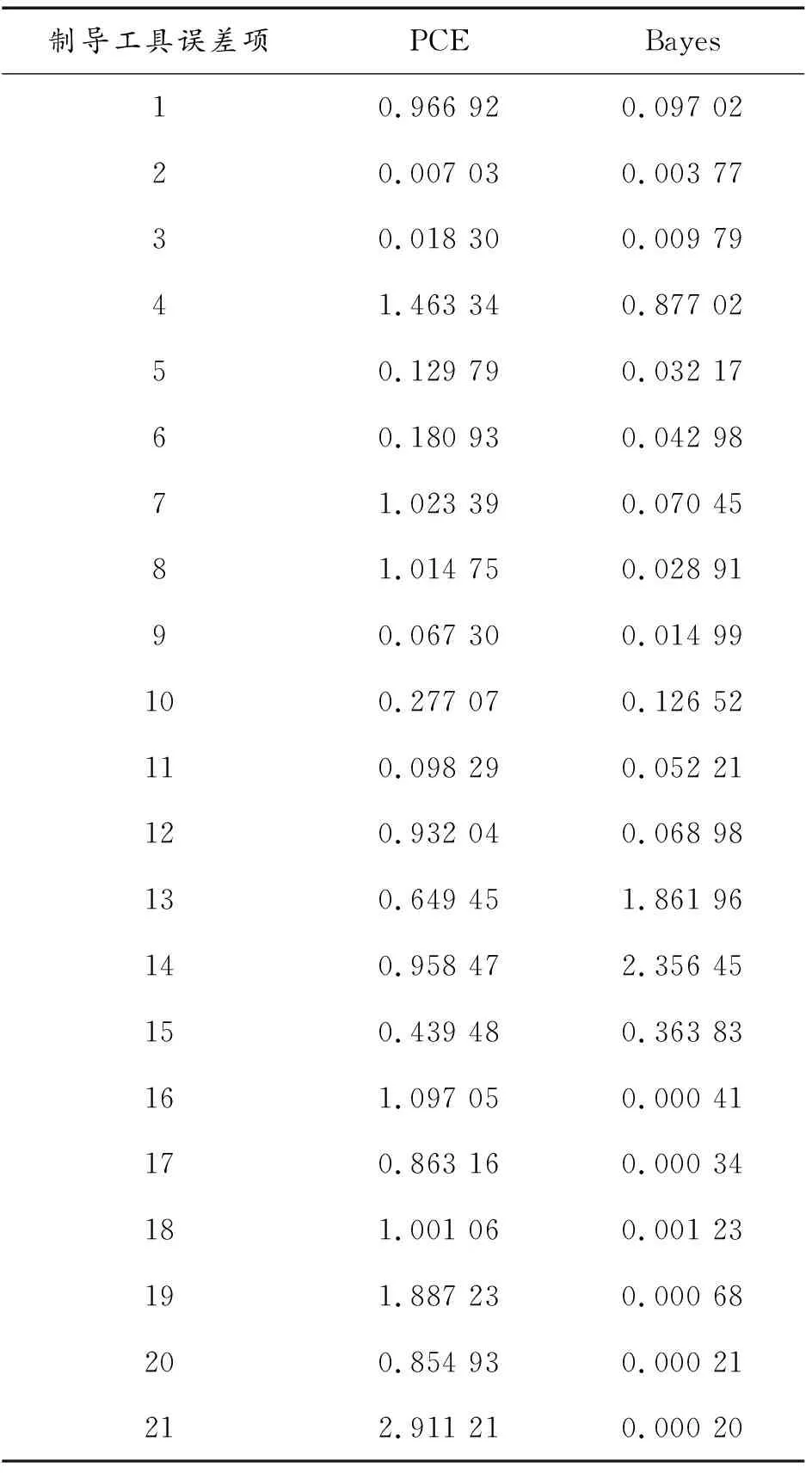
表1 1 000次MC實驗制導工具誤差估計的平均誤差比

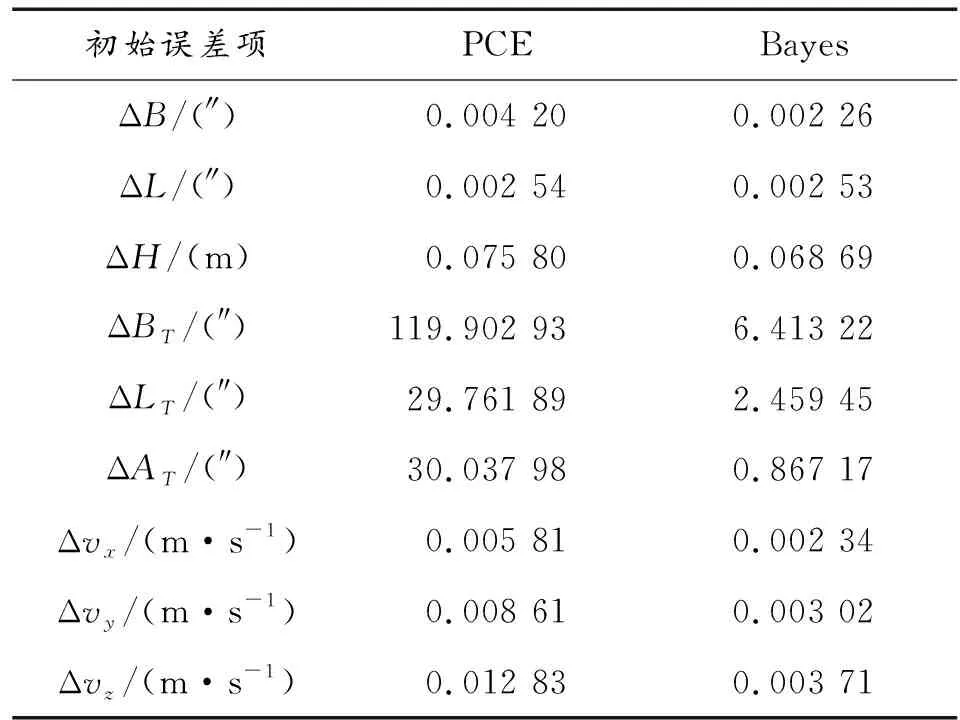
表2 1 000次MC實驗初始誤差估計的均方根誤差

4 結論

本文研究動基座發射飛行器的初始誤差和制導工具誤差的估計問題，采用線性化近似方法建立了同時估計初始誤差和制導工具誤差的線性模型，利用Bayes估計方法解決了環境函數矩陣的復共線性。仿真結果表明：該方法的估計精度優于PCE方法。本方法能夠為動基座發射飛行器的精度鑒定提供有力支撐。