艦載機牽引系統的動力學建模與仿真
范加利,朱興動,宋建華,王 正
(1.海軍航空大學青島校區, 山東 青島 260041; 2.海軍航空大學訓練部, 山東 煙臺 264001)
轉運作業是艦載機艦基保障的重要組成部分,在飛行甲板或機庫甲板,艦載機的轉運作業由牽引車頂推或牽引實現。目前,世界各國航母的艦載機轉運主要依靠有經驗的牽引車駕駛員操縱牽引車完成。隨著駐艦艦載機種類和數量的增加,牽引車操縱頻繁,這就對牽引的安全性和快速性提出了更高的要求。
為了便于后續開展艦載機牽引系統的路徑規劃和跟蹤方法的深入研究,本文針對牽引系統運動速度低、牽引車、艦載機和牽引桿之間的鉸接角較大,艦載機參數差異大,牽引系統同時存在完整約束和非完整約束等特點,基于物理特性和機械運動的基本概念,建立牽引系統通用模型。首先,以有桿牽引車組成的牽引系統為對象,根據非完整約束特性,引入廣義速度,建立系統的運動學模型,然后,通過適當地定義質量和角速度矩陣,采用經典的牛頓-歐拉方程描述系統動力學特性,模型推導中不需考慮兩個鉸接點處的力和力矩。最終獲得的模型可以作為使用無桿牽引車的艦載機牽引模型特例。
1 國內外研究現狀
艦載機調運是航母艦載機艦基保障的重要環節,它影響著艦載機的出動強度,對航空戰斗力生成具有重要作用。
近年來,國內外學者對艦載機調運問題進行了大量研究。從相關文獻報道看,大致分為艦載機牽引軌跡控制與牽引技術虛擬訓練[1-3]、艦載機艦面調運路徑規劃[4-7]以及艦載機調度[8]。這三個方面研究既有區別,又有聯系。艦載機調度問題是從最頂層規劃艦面保障資源,最優安排艦載機的布列、轉運、機務保障等各個環節。艦載機路徑規劃主要研究甲板環境下,如何移動艦載機達到時間和安全性最優,它是研究調度問題的基礎。艦載機牽引系統的路徑控制關注艦載機路徑的實現,它與路徑規劃問題相關。
本文的研究內容是艦載機路徑規劃與路徑跟蹤控制的基礎。關于艦載機牽引系統模型方面的研究,文獻[1-2]建立了艦載機牽引系統的側向運動模型,研究了牽引系統的行駛穩定性和自動轉向控制問題,文獻[4],在相關假設下,建立了牽引系統的運動學模型,研究了艦載機的避碰監視,文獻[5],基于艦載機的運動學模型,研究了艦載機甲板避碰路徑規劃。上述文獻中建立的艦載機牽引系統模型均具有一定的局限性。艦載機牽引系統屬于一類具有非完整約束特性的多體鉸接系統,系統動力學和運動學分析較為復雜,文獻[9-11]對該類系統進行了大量研究,取得可供借鑒的結論。
2 牽引系統建模
2.1 運動學模型
飛行甲板上,使用有桿牽引車牽引艦載機的示意圖如圖1。
取牽引車后軸中心坐標為(xt,yt),艦載機主輪中心坐標為(xa,ya),牽引桿與牽引車縱軸線間的夾角為β1,牽引桿與艦載機縱軸線間的夾角為β2,艦載機和牽引車的航向角分別為θa和θt,牽引車前輪轉角為δ,牽引車縱向速度為vt,lt為牽引車前后輪軸之間的軸距,lb為牽引桿長度,lt為艦載機前輪與主輪之間的距離,c1為牽引車后軸距牽引車尾鉤的距離。建模中做如下假設:
(1)整個牽引系統在甲板面做平面運動,且艦載機和牽引車各輪運動中均無滑動。
(2)牽引車和艦載機的運動和動態均關于各自的縱軸對稱。
(3)牽引系統中各機輪與甲板面的接觸連續,即作業過程中機輪均不離開甲板面。
(4)牽引車與牽引車和艦載機的鉸接點無摩擦。
(5)忽略甲板的復合運動對艦載機牽引系統的影響。
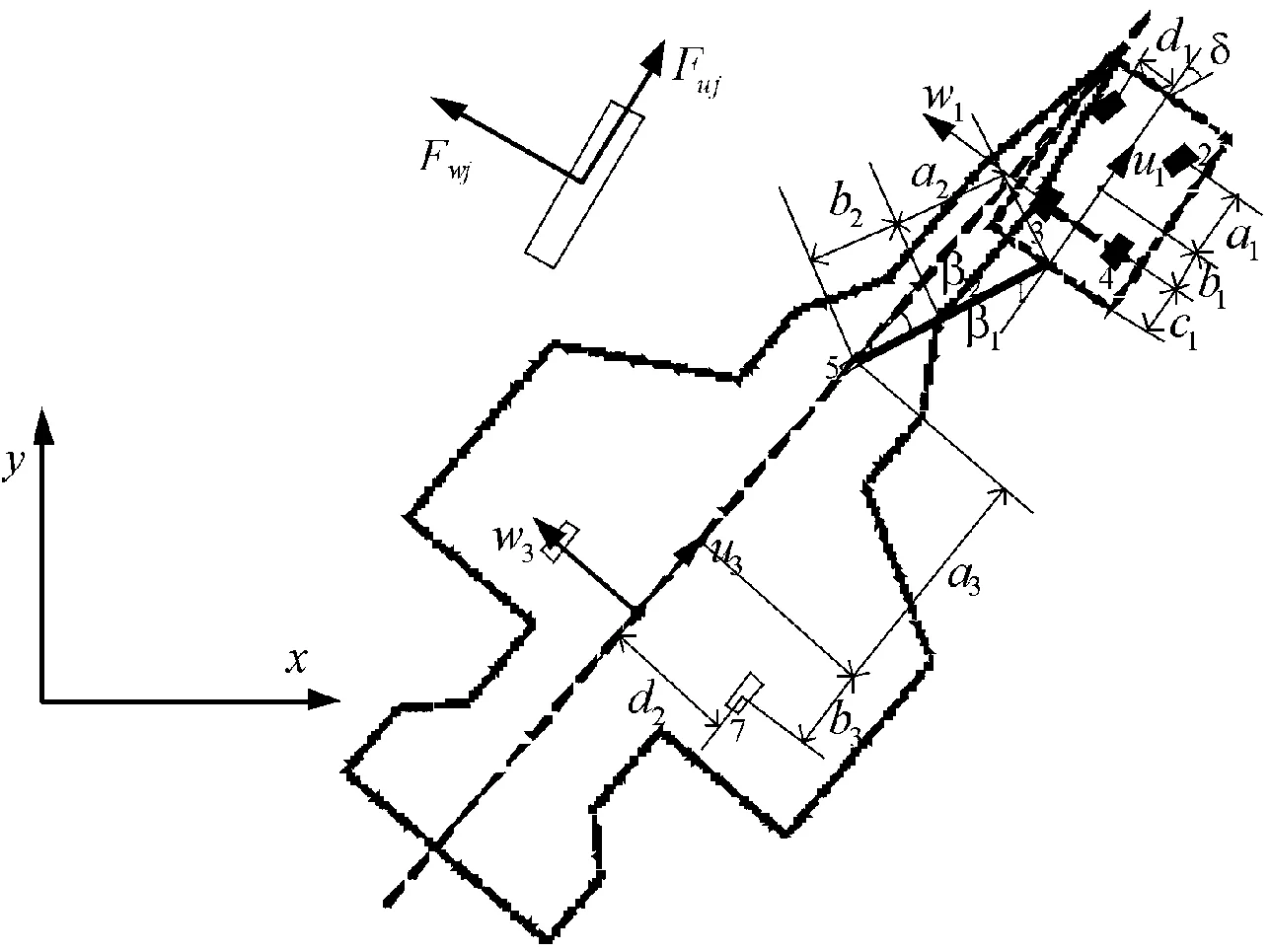
圖1 艦載機牽引示意圖
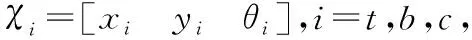
xa=xt-c1cosθt-lbcos(θt+β1)-lacos(θ+β1+β2)
ya=yt-c1sinθt-lbsin(θt+β1)-lasin(θ+β1+β2)
θa=θt+β1+β2
(1)
其中,lb=a2+b2,la=a3+b3。
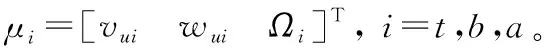
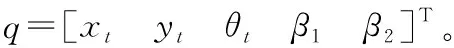
(2)
其中:
在假設式(3)條件下,根據系統的非完整約束特性,可定義標量廣義速度α=vut。建立系統的運動學模型為
(3)
其中:
考慮系統實際存在的機械約束,牽引車前輪轉角δ、牽引車縱軸與牽引桿之間的夾角β1以及牽引桿和艦載機縱軸之間的夾角β2均存在機械約束,即:
|β1|≤β1max,|β2|≤β2max
(4)
|δ|≤δmax
(5)
2.2 動力學模型
根據式(2)和式(3),速度向量μ和廣義速度的關系即:
μ=Jh(q)Jnh(q,δ)α=J(q,δ)α
(6)
其中J(q,δ)為:
(7)
定義牽引系統中每一部分的擴展質量矩陣為Mi=diag(mi,mi,Ji),i=t,b,a,定義M=diag(Mt,Mb,Ma),其中mi是第i個部分的質量,Ji每一部分相對于各自重心的轉動慣量(在平面內繞各自縱軸旋轉),類似地,定義擴展的角速度矩陣:
且W=diag(Wt,Wb,Wa)。
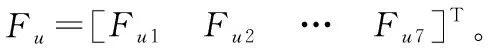
Fui=μaNi
(8)
μa是滾動摩擦因數,Ni是個輪胎承受的垂直載荷。
主動力和力矩向量見式(9)。
(9)
利用上述表達式,可計算慣性力、向心力和哥氏力分別為:
D(q,δ)=JT(q,δ)MJ(q,δ)
(10)
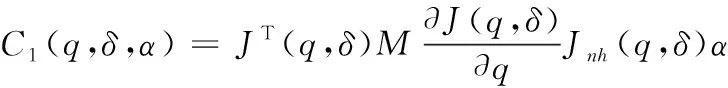
(11)
(12)
只考慮縱向速度的系統動力學模型為
JT(q,δ)Γu(δ,β2,Fu)}
(13)
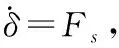
3 仿真研究
采用若干模擬設備,模擬艦載機、牽引車和牽引桿,模擬牽引車前輪轉向,后輪驅動。牽引系統中各參數取值如下,a1=1 m,b1=1.4 m,c1=1.2 m,a2=b2=2 m,a3=4 m,b3=2 m,d1=1.15 m,d2=2.4 m,mt=3×103kg,mb=150 kg,ma=2.4×104kg,Ja=2 364 kg·m2,Jt=35 720 kg·m2。機械約束取值為:β1max=1.2 rad,β2max=0.78 rad,δmax=0.3 rad。
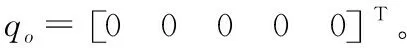
在Matlab環境下,基于文中建立運動學模型,研究牽引系統的運動學特性。牽引系統參數和初始位姿不變,對牽引車轉向角取為δ=0.1δmax時,分別仿真牽引和頂推作業的系統響應,結果如圖6~圖8所示,從圖中可以發現此時系統仍按圓弧路徑機動,但圓弧半徑明顯增多,頂推時,β1和β2仍很快達到飽和值。令δ=0,α=±1 m/s,在20 s時對β1角加入0.1 rad的擾動,仿真結果如圖9~圖13所示,從仿真結果可以看出,正向牽引時,系統能夠克服夾角擾動,這對應于實際系統中艦載機發生側向滑移的情形,而對于逆向頂推,存在擾動時系統立刻發散,呈現折疊效應。
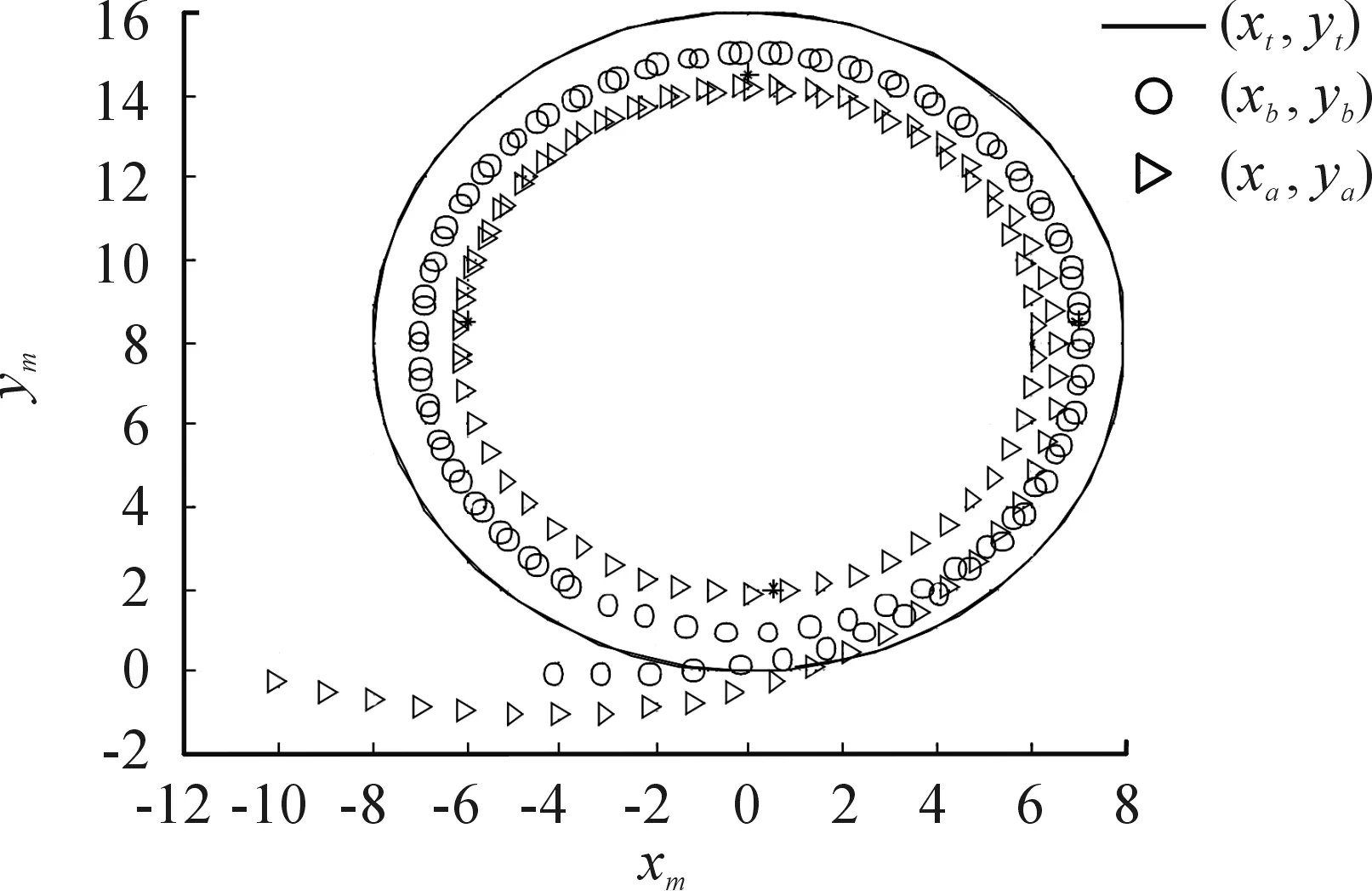
圖2 正向牽引位置曲線
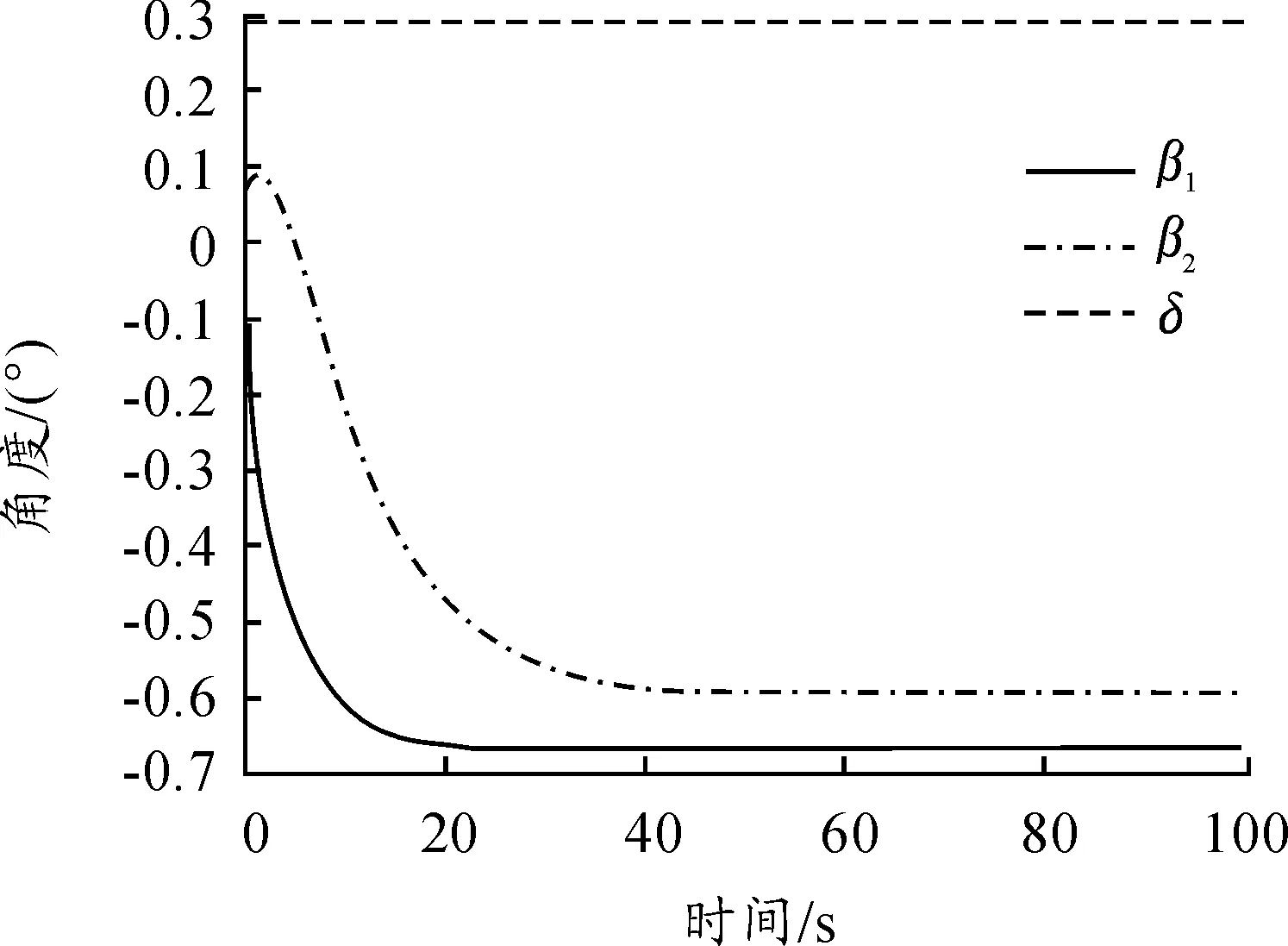
圖3 正向牽引角度響應曲線
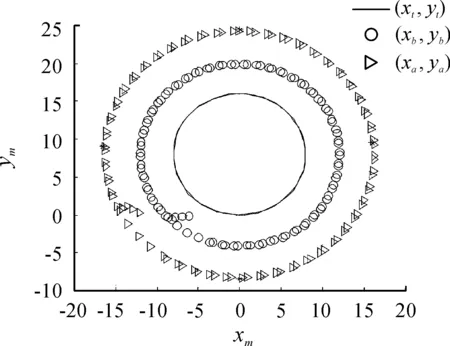
圖4 逆向頂推位置曲線
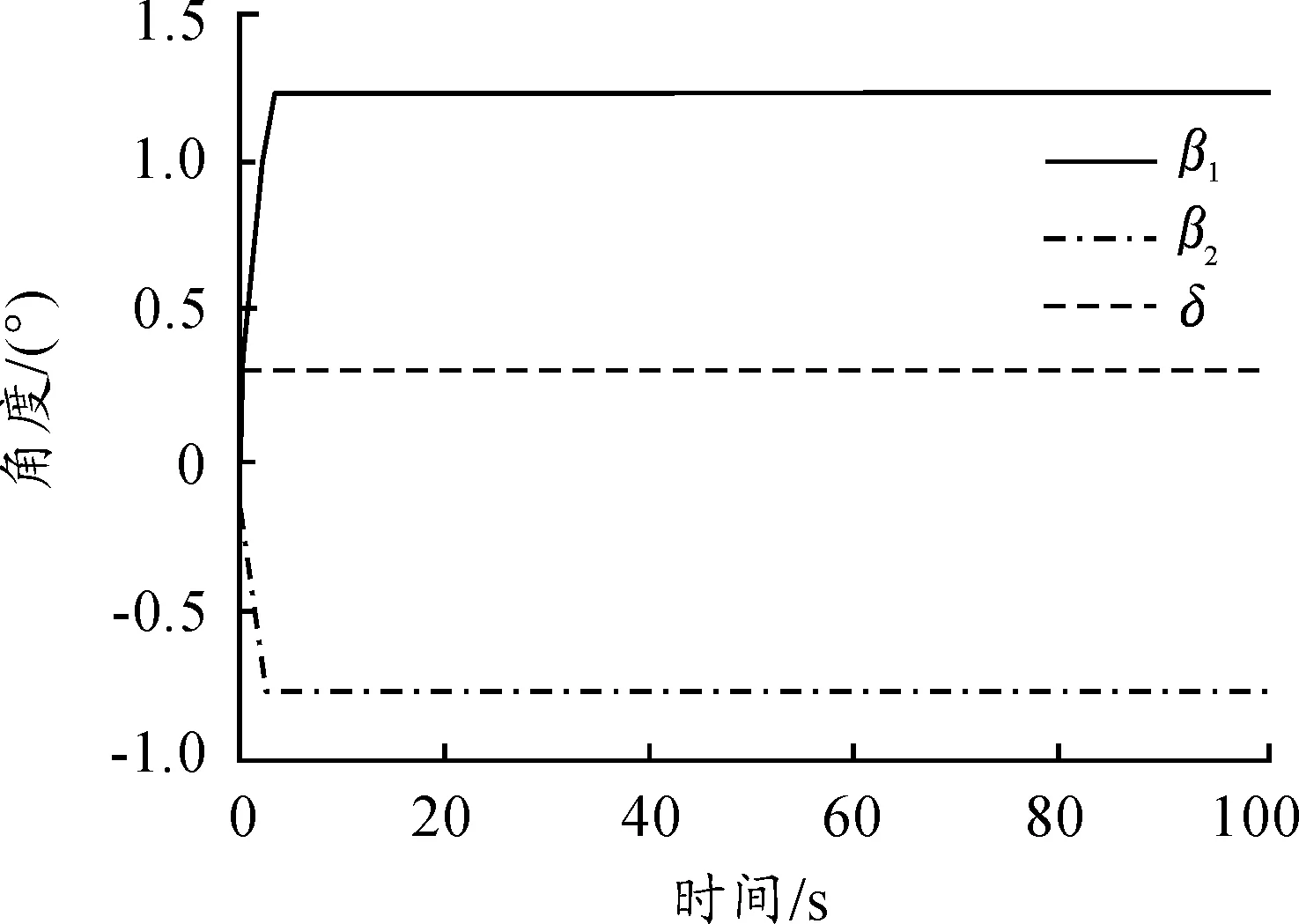
圖5 逆向頂推角度響應曲線
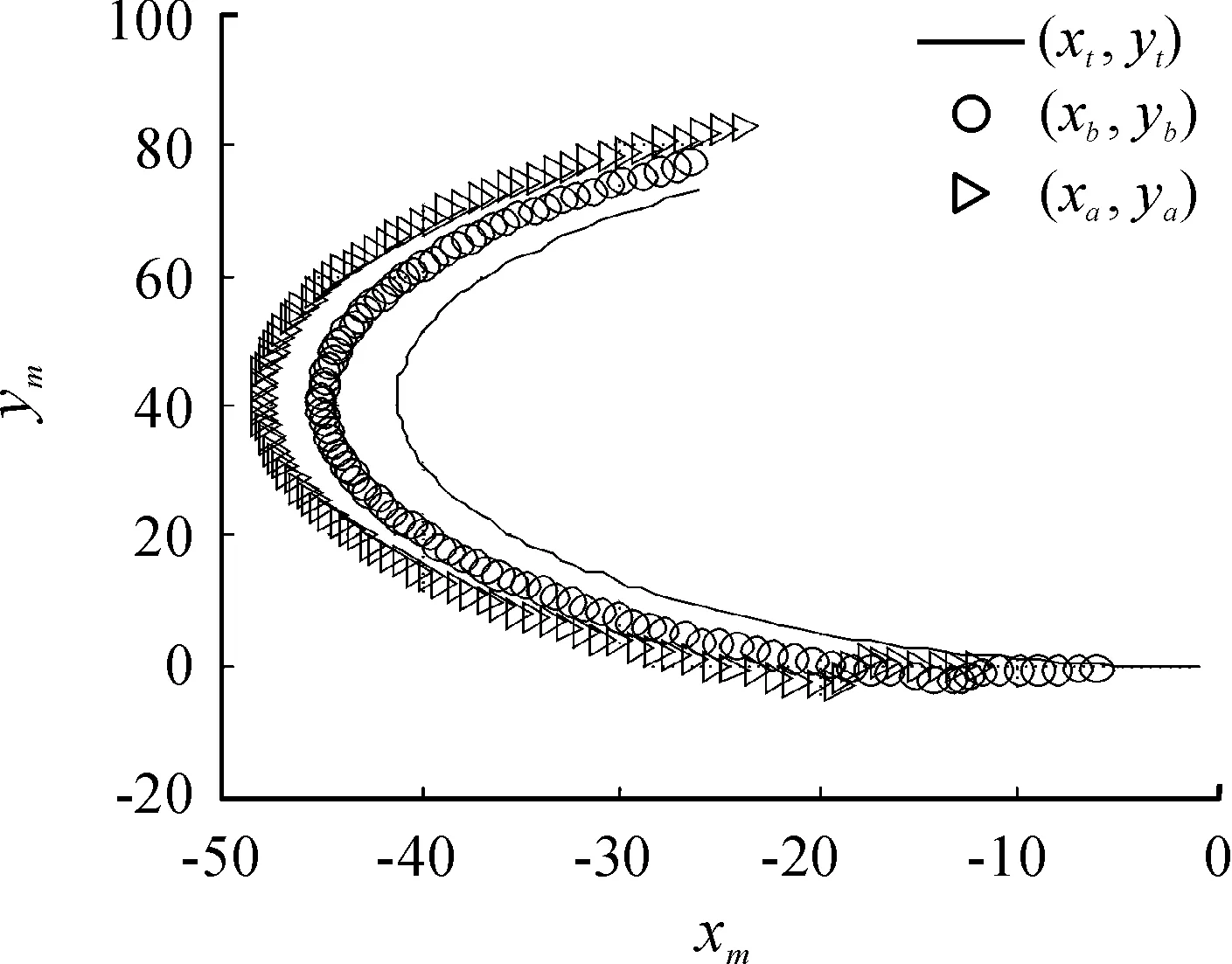
圖6 δ=0.1δmax逆向頂推位置響應
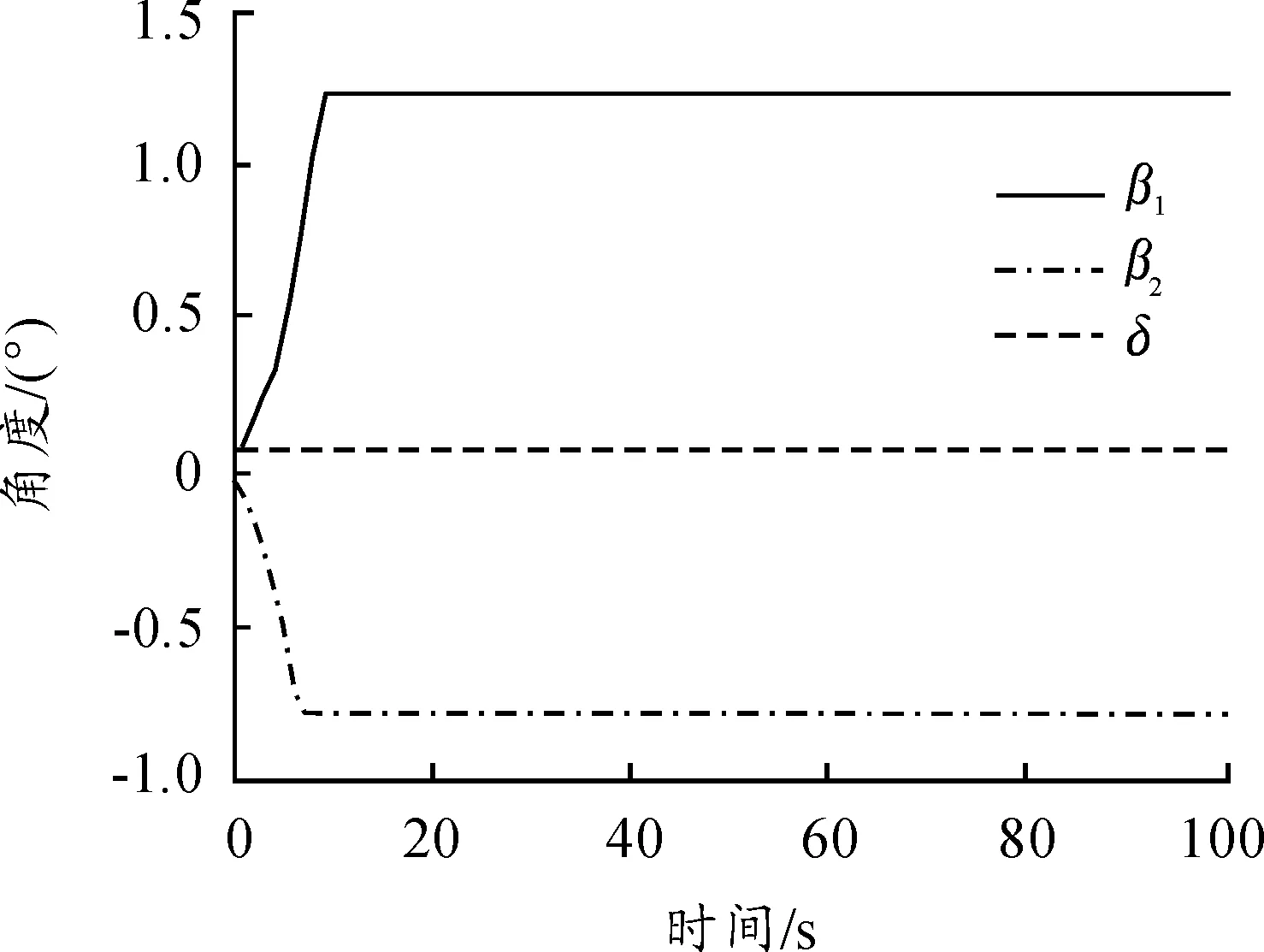
圖7 δ=0.1δmax逆向頂推角度響應
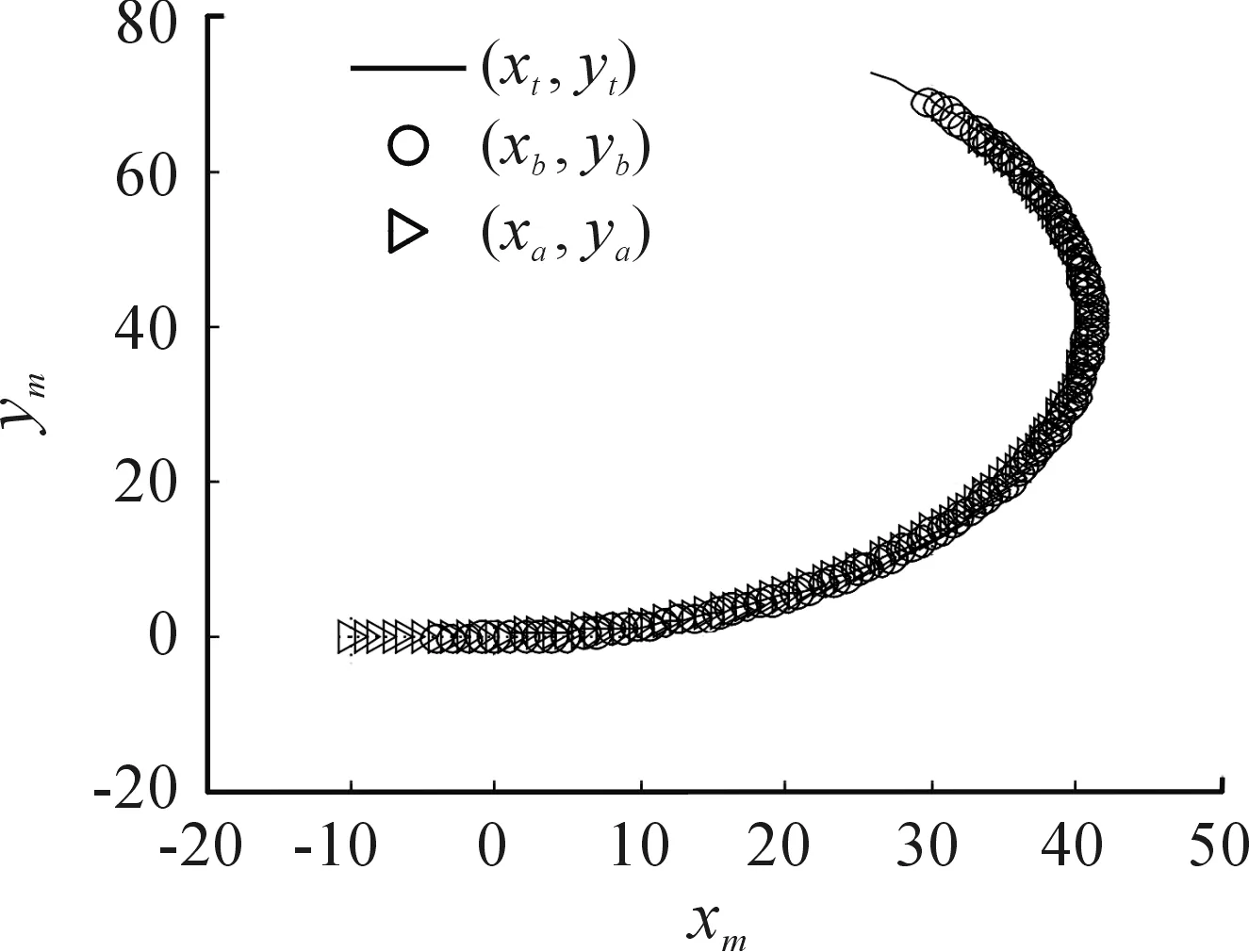
圖8 δ=0.1δmax牽引位置響應
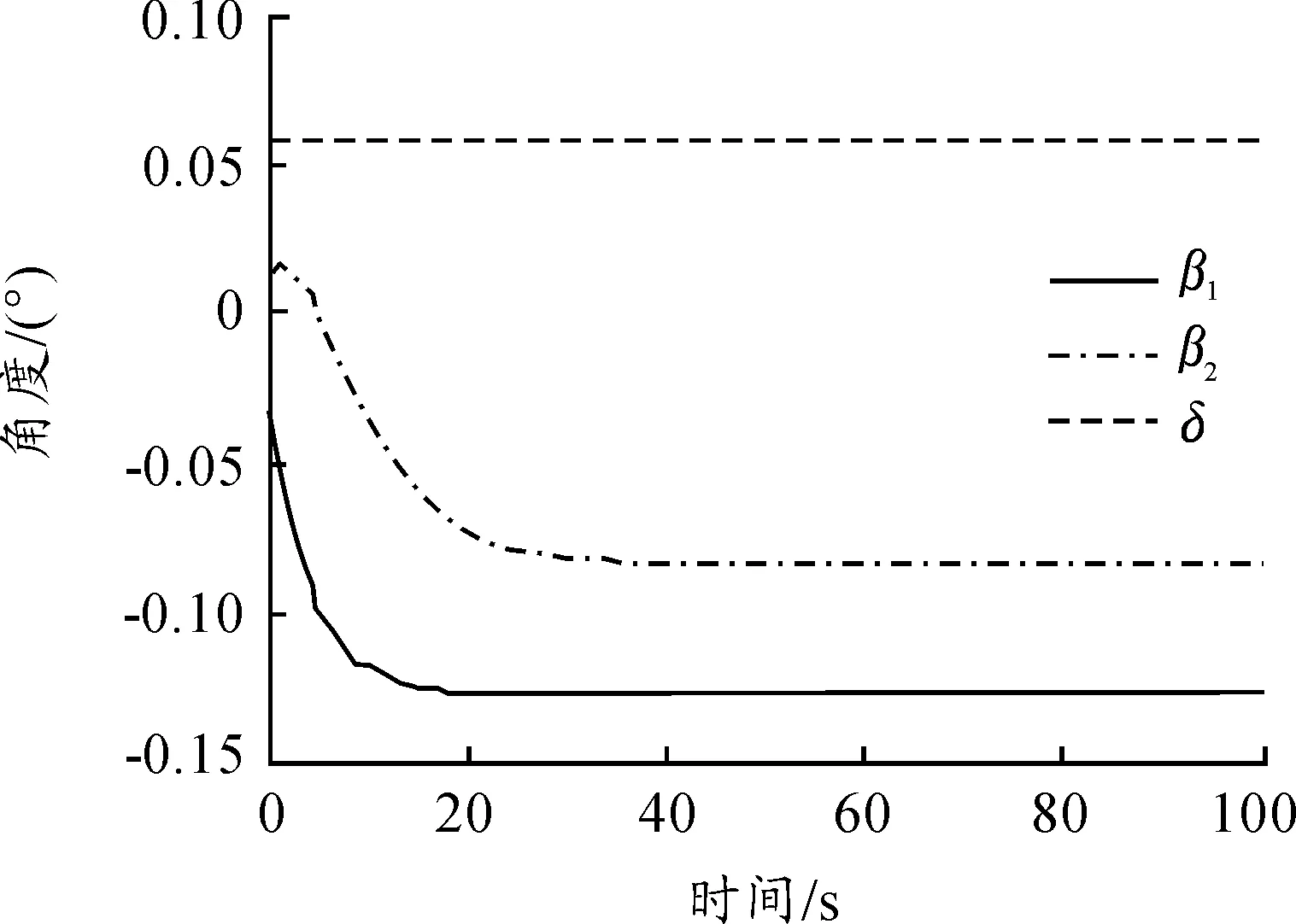
圖9 δ=0.1δmax牽引角度響應
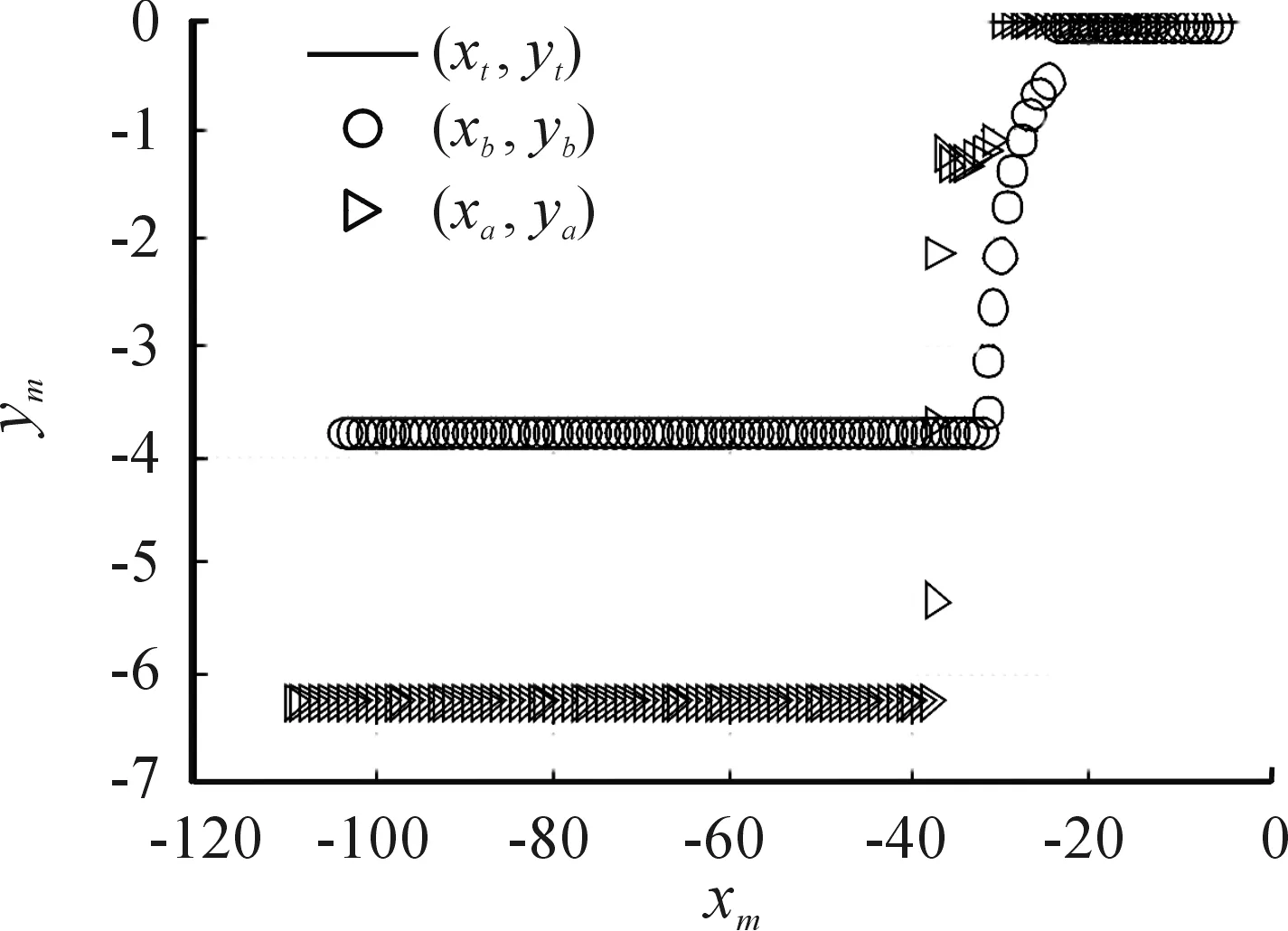
圖10 δ=0頂推加擾動位置響應
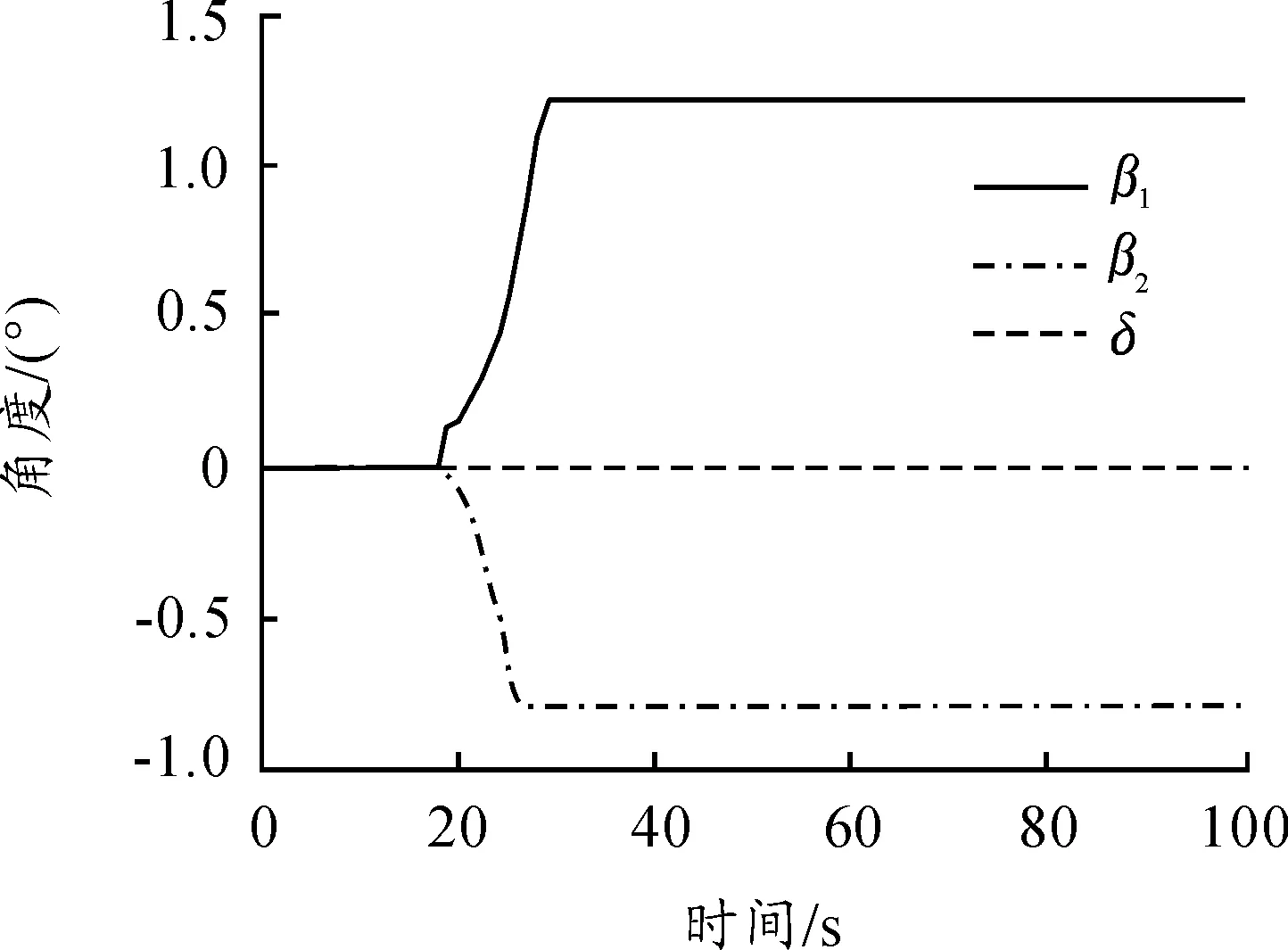
圖11 δ=0頂推加擾動角度響應
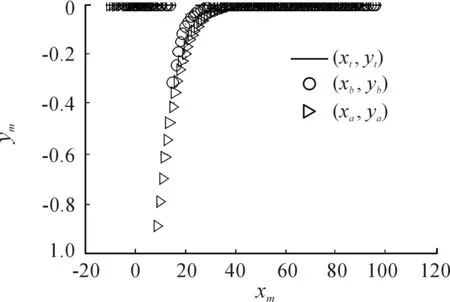
圖12 δ=0牽引加擾動位置響應
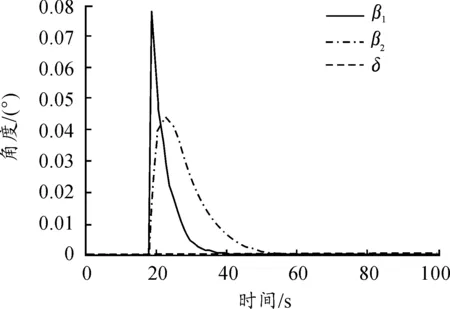
圖13 δ=0牽引加擾動角度響應
4 結論
1) 驗證了所建模型的正確性,該模型既適用于有桿牽引車牽引系統也適用于無桿牽引車構成的牽引系統建模。
2) 文中建立的模型適合用于艦載機牽引系統路徑規劃和路徑跟蹤的算法研究。艦載機牽引系統正向牽引時,系統處于穩定狀態,可克服擾動,而逆向頂推時,由于折疊效應的影響,系統不穩定,要求牽引車駕駛員在頂推作業時必須及時調整牽引車前輪輸入角,避免艦載機前輪長期處于極限轉彎狀態。

