葉片式渦流發(fā)生器對(duì)壓縮拐角流動(dòng)分離的控制

胡萬(wàn)林，于劍，劉宏康，趙淵，閻超

北京航空航天大學(xué) 航空科學(xué)與工程學(xué)院，北京 100083

在超聲速飛行器的內(nèi)外流動(dòng)中普遍存在著流動(dòng)分離的現(xiàn)象，包括激波誘導(dǎo)的邊界層分離、繞流引起的分離、尾跡區(qū)的分離等[1]。激波誘導(dǎo)的邊界層分離會(huì)造成較大的能量損失，增大阻力，并伴隨有非定常效應(yīng)[2]。對(duì)飛行器的穩(wěn)定性和操控性帶來(lái)影響，特殊區(qū)域的流動(dòng)分離再附還會(huì)引起嚴(yán)峻的局部氣動(dòng)加熱現(xiàn)象，對(duì)飛行器造成一定的危害。因此，對(duì)流動(dòng)分離進(jìn)行有效控制就具有非常實(shí)際的工程意義。

渦流發(fā)生器作為一種被動(dòng)控制技術(shù)，將動(dòng)量從外部高速流輸運(yùn)到邊界層內(nèi)，加強(qiáng)邊界層低速區(qū)的能量，增強(qiáng)邊界層抵抗逆壓梯度的能力[3]。按其尺寸可分為傳統(tǒng)渦流發(fā)生器(VGs，其高度h與邊界層的厚度δ之比h/δ～1)和微型渦流發(fā)生器(MVGs，h/δ在0.1～0.5之間，又被稱為低形阻渦流發(fā)生器[4])，因其結(jié)構(gòu)簡(jiǎn)單和經(jīng)濟(jì)性而被廣泛研究。1947年，Taylor[5]首次提出了渦流發(fā)生器的概念,隨后被廣泛應(yīng)用于航空領(lǐng)域，延遲邊界層分離[6]，提升機(jī)翼的升阻力特性[7-10]，降低機(jī)體后的阻力[11]等。Brown等[12]于1967年，研究了渦流發(fā)生器對(duì)于亞聲速擴(kuò)壓管邊界層分離的控制效果，發(fā)現(xiàn)用特制的渦流發(fā)生器能減小壓力損失并使得流場(chǎng)均勻。然而傳統(tǒng)的渦流發(fā)生器形阻較大，其實(shí)用性為人所質(zhì)疑。微渦流發(fā)生器于20世紀(jì)70年代開(kāi)始為人們所研究，Kuethe[13]用波浪形的微型渦流發(fā)生器控制尾跡區(qū)的流動(dòng)，減小了其聲學(xué)上的擾動(dòng)。Ashill等[14]于2001年結(jié)合試驗(yàn)與理論研究了微型渦流發(fā)生器尾跡區(qū)的流動(dòng)結(jié)構(gòu)，并應(yīng)用于跨聲速機(jī)翼的流動(dòng)，達(dá)到了增升減阻的目的。Anderson等[15]于2006年對(duì)微三角楔的形狀進(jìn)行優(yōu)化研究，提出了一套優(yōu)化尺寸。基于Ashill、Anderson等的微三角楔形渦流發(fā)生器，張慶虎[1]于2013年試驗(yàn)研究了這兩種渦流發(fā)生器對(duì)于4種邊界層分離的控制效果，精細(xì)顯示了其流場(chǎng)結(jié)構(gòu)，并分析其時(shí)間演化特性。2016年Schreyer等[16]用試驗(yàn)和大渦模擬(LES)數(shù)值方法研究了微斜楔渦流發(fā)生器誘導(dǎo)的流向渦對(duì)于壓縮拐角分離區(qū)的激波邊界層干擾的影響。

近年來(lái)，微型渦流發(fā)生器以其低形阻、經(jīng)濟(jì)等特性，成為眾多科研工作者們研究的熱點(diǎn)[17-18]。雖然前人對(duì)于渦流發(fā)生器的相關(guān)研究較為充分，其應(yīng)用也逐步成熟，然而，有關(guān)利用葉片式渦流發(fā)生器控制壓縮拐角處的邊界層分離方面的研究較少，其控制機(jī)制與性能尚不明確。因此，本文運(yùn)用數(shù)值模擬的方法研究超聲速壓縮拐角引起的激波邊界層干擾現(xiàn)象，并分析梯形葉片式渦流發(fā)生器的幾何參數(shù)對(duì)其控制效果的影響。

1 物理模型

葉片式渦流發(fā)生器放置位置如圖1所示，其后緣距平板前緣400 mm，距拐角處100 mm，無(wú)控制時(shí)當(dāng)?shù)剡吔鐚雍穸圈?7.5 mm。其擺放方式，主要分為相向旋轉(zhuǎn)(Counter-rotating,Ct)和同向旋轉(zhuǎn)(Co-rotating,Co)，如圖2和圖3所示。各渦流發(fā)生器的幾何參數(shù)見(jiàn)表1，尺寸標(biāo)注如圖4所示。表1中Ct1～Ct7為相向旋轉(zhuǎn)計(jì)算實(shí)例，Co1為同向旋轉(zhuǎn)計(jì)算實(shí)例。渦流發(fā)生器后緣高度為h，底邊長(zhǎng)度為e，葉片厚度為d,前緣后掠角度β=30°，渦流發(fā)生器與來(lái)流方向夾角α=23°，相向旋轉(zhuǎn)時(shí)角度相反，同向旋轉(zhuǎn)葉片后緣間距為λ，相向旋轉(zhuǎn)葉片后緣間距為η，沿展向布置葉片的對(duì)數(shù)為n，沿展向布置多個(gè)渦流發(fā)生器用于模擬葉片間的相互作用。

圖5為渦流發(fā)生器局部壁面及對(duì)稱面網(wǎng)格。采用多塊對(duì)接結(jié)構(gòu)網(wǎng)格，網(wǎng)格總量在1 000～2 500萬(wàn)之間。入口、出口及頂部為遠(yuǎn)場(chǎng)邊界，兩側(cè)面為對(duì)稱邊界。

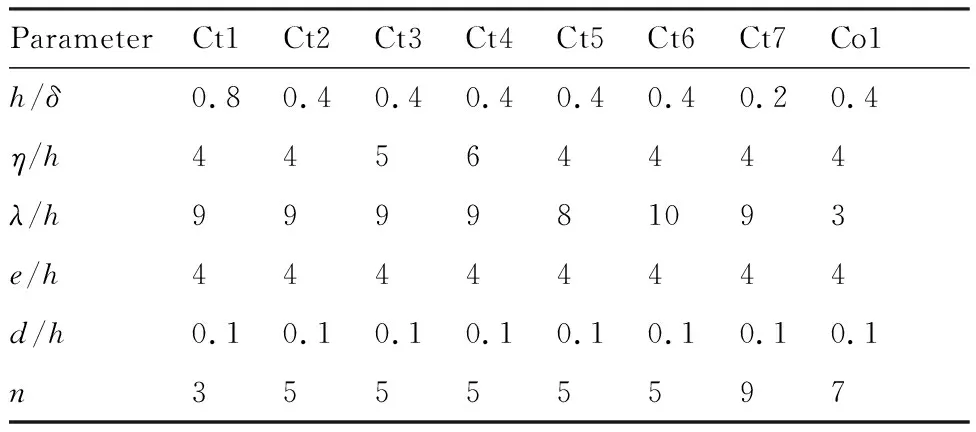
ParameterCt1Ct2Ct3Ct4Ct5Ct6Ct7Co1h/δ0.80.40.40.40.40.40.20.4η/h44564444λ/h999981093e/h44444444d/h0.10.10.10.10.10.10.10.1n35555597

2 湍流模型驗(yàn)證

本文采用定常狀態(tài)計(jì)算，模擬渦流發(fā)生器對(duì)24°壓縮拐角邊界層分離的流動(dòng)控制作用。本質(zhì)上，帶有葉片式渦流發(fā)生器的壓縮拐角的流動(dòng)是非定常的，但是模擬葉片式渦流發(fā)生器幾何參數(shù)對(duì)于其控制作用的影響，側(cè)重于反應(yīng)宏觀上的統(tǒng)計(jì)規(guī)律，利用定常的雷諾平均Navier-Stokes(RANS)方法是合適的。基于本文CFD求解器，趙瑞和閻超[19]分別采用了Spalart-Allmaras(S-A)湍流模型、k-ω兩方程模型、Shear Stress Transport(SST)湍流模型對(duì)超聲速壓縮拐角進(jìn)行了數(shù)值模擬，并與試驗(yàn)[20]對(duì)比。結(jié)果表明，對(duì)于24°壓縮拐角，S-A與SST模型分離區(qū)物面壓力預(yù)測(cè)結(jié)果偏大,而k-ω計(jì)算結(jié)果偏小，S-A與SST模型預(yù)測(cè)分離點(diǎn)提前,再附點(diǎn)滯后,分離區(qū)過(guò)大,而k-ω模型雖然預(yù)測(cè)分離點(diǎn)與再附點(diǎn)均稍有滯后,但預(yù)測(cè)的分離區(qū)大小較為準(zhǔn)確，對(duì)于本文的研究較合適。本文數(shù)值模擬的來(lái)流條件見(jiàn)表2，表中Ma∞、p∞、T∞分別為來(lái)流參數(shù)馬赫數(shù)、密度、壓力和溫度，Re為單位雷諾數(shù)。

表2 來(lái)流條件Table 2 Freestream conditions

3 相向旋轉(zhuǎn)葉片式渦流發(fā)生器的控制效果

3.1 空間流動(dòng)結(jié)構(gòu)

圖 6為安裝h=0.4δ的相向旋轉(zhuǎn)式VGs后，壁面壓力(p)分布及其空間流線(馬赫數(shù)Ma著色)。氣流流過(guò)VGs葉片后，卷起一對(duì)方向相反的流向渦，增大了主流與邊界層的動(dòng)量輸運(yùn)；在相鄰兩對(duì)VGs中間處，氣流平直流過(guò)，并未有分離渦產(chǎn)生。

圖 7給出了不同站位處(x-x1=h、5h、10h、15h，x為流向坐標(biāo)，x1為VGs后緣處的坐標(biāo))流向無(wú)量綱渦量(ωxh/u0,ωx為x方向的渦量，u0為來(lái)流速度)分布，圖中實(shí)線為流線，虛線為無(wú)控制時(shí)當(dāng)?shù)剡吔鐚铀谖恢谩Ｔ赩Gs后流向渦強(qiáng)度逐漸衰減，但渦核位置貼近壁面，在法向上并未有明顯上升，流向渦主要在邊界層內(nèi)，對(duì)主流的影響不大。

本文求流向渦環(huán)量采用Q準(zhǔn)則[21]，如式(1)所示，提取Q=0時(shí)的輪廓線作為渦核區(qū)域的邊界，并沿邊界進(jìn)行曲線積分求得環(huán)量Г,如式(2)所示，用來(lái)流速度u0和VGs后緣高度h進(jìn)行無(wú)量綱化。

(1)

(2)

式中：Ω和S分別為速度梯度的反對(duì)稱與對(duì)稱張量；Г為環(huán)量大小；u、v、w分別為x、y、z方向的速度；l為旋渦邊界曲線。

圖 8給出了無(wú)控制和有控制時(shí)壁面摩擦力系數(shù)(Cf)分布云圖，無(wú)控制時(shí)上游分離點(diǎn)及下游再附點(diǎn)距轉(zhuǎn)折處長(zhǎng)度分別為L(zhǎng)s=19.10 mm和Lr=11.07 mm。安裝0.4δ高度的MVGs后，在其尾部分離再附區(qū)顯著減小，而在相鄰兩對(duì)MVGs中的尾部分離再附區(qū)反而有所增加，為綜合考量VGs對(duì)于邊界層分離的控制作用，求分離區(qū)長(zhǎng)度的平均值可得Ls=14.47 mm、Lr=3.73 mm，對(duì)比無(wú)控制的結(jié)果，Ls約減小24.24%，Lr約減小66.31%，總長(zhǎng)度L約減小了39.68%。文中有控制時(shí)所述分離區(qū)長(zhǎng)度均指平均長(zhǎng)度。

3.2 壁面壓力分布曲線及速度型曲線

圖 9給出了無(wú)控制時(shí)壓縮拐角對(duì)稱面處及安裝相向旋轉(zhuǎn)VGs后特征位置處(相向旋轉(zhuǎn)葉片中心線A、葉片后緣B、相鄰兩對(duì)葉片中心線C)壁面無(wú)量綱壓力分布，圖中x0為拐角處坐標(biāo)。可看出，無(wú)控制時(shí)(對(duì)應(yīng)圖中Clean)，斜坡產(chǎn)生的高壓力通過(guò)邊界層傳遞到上游，使得在拐角前壓力有所升高。安裝VGs后，減弱了轉(zhuǎn)角處的分離，使得在轉(zhuǎn)折點(diǎn)前壁面壓力緩慢增大，在轉(zhuǎn)折點(diǎn)附近較原始?jí)毫Φ停谵D(zhuǎn)折點(diǎn)后，B、C處壁面壓力恢復(fù)到未安裝VGs之前的壓力值，而A處由于流向渦的再附使得壁面壓力明顯增大。

圖10給出了x=-4δ(分離區(qū)前)截面處沿壁面法向(y方向)的速度型曲線。可看出，過(guò)A處的速度型最飽滿，在y<0.5δ時(shí)，邊界層內(nèi)的速度大于無(wú)控制時(shí)的速度；過(guò)B處及C處的速度型曲線不及無(wú)控制時(shí)飽滿，過(guò)B處，在y很小時(shí)，邊界層內(nèi)的速度略大于無(wú)控制時(shí)的速度，而過(guò)C處，邊界層內(nèi)存在著回流。

3.3 對(duì)分離區(qū)流動(dòng)結(jié)構(gòu)的控制效果

4 渦流發(fā)生器幾何參數(shù)的影響

圖12給出了無(wú)控制和有控制時(shí)分離再附區(qū)無(wú)量綱平均長(zhǎng)度(L/δ)的柱狀圖。無(wú)控制時(shí)分離區(qū)長(zhǎng)度L約為3.9δ，其中Ls約為2.5δ，Lr約為1.4δ。計(jì)算結(jié)果表明，各渦流發(fā)生器均能控制壓縮拐角處的分離區(qū)，且Lr減小幅度更大。圖 13給出了無(wú)控制和有控制時(shí)阻力系數(shù)(CD)的大小，安裝VGs后系統(tǒng)的阻力均有些許增大。

圖 14給出了各不同參數(shù)影響下的壁面無(wú)量綱壓力分布以及不同流向位置處(x-x1=h、5h、10h、15h、20h)的無(wú)量綱環(huán)量大小，R1、R2分別表示中心線一側(cè)第1個(gè)和第2個(gè)渦旋。對(duì)于壁面壓力分布，不同幾何參數(shù)的影響主要體現(xiàn)于分離區(qū)內(nèi)。對(duì)于各葉片尾跡區(qū)無(wú)量綱環(huán)量分布，其規(guī)律與Hunt等[22]結(jié)論相似，沿流向逐漸減小，且趨于平緩。

對(duì)比不同擺放方式的VGs (Ct2、Co1)的控制效果。圖12表明，對(duì)于兩種擺放方式的VGs，分離再附區(qū)總長(zhǎng)度L相當(dāng)，但同向旋轉(zhuǎn)方式，分離點(diǎn)距轉(zhuǎn)折點(diǎn)的距離Ls較小，可知同向旋轉(zhuǎn)方式的VGs利于減小Ls的大小，相向旋轉(zhuǎn)方式的VGs利于減小Lr的大小。同時(shí)，圖13表明同向旋轉(zhuǎn)方式的系統(tǒng)阻力更小。對(duì)比壁面壓力分布規(guī)律，在轉(zhuǎn)折點(diǎn)前，同向旋轉(zhuǎn)VGs壁面壓力略低于相向旋轉(zhuǎn)VGs，改善了分離區(qū)的壓力分布。過(guò)中心線A處，相向旋轉(zhuǎn)VGs的壁面壓力出現(xiàn)一個(gè)峰值，而同向旋轉(zhuǎn)的VGs壁面壓力則緩慢增大無(wú)明顯峰值。對(duì)比其尾跡區(qū)流向渦環(huán)量的大小，相向旋轉(zhuǎn)的VGs，各葉片后渦強(qiáng)度相當(dāng)，而同向旋轉(zhuǎn)葉片R1處比R2處略小，在遠(yuǎn)離VGs的后方差值越大，且同向旋轉(zhuǎn)葉片環(huán)量較相向旋轉(zhuǎn)的略大，如圖 14(a)所示。

對(duì)比不同高度(h)VGs (Ct1、Ct2和Ct7)的控制效果。圖 12表明，h越大Ls、Lr減小幅度均越大。圖13表明，系統(tǒng)的阻力在h=0.4δ時(shí)最小，h=0.2δ較h=0.4δ系統(tǒng)阻力增大的更多，經(jīng)分析認(rèn)為可能是所用VGs的數(shù)目更多所致。在分離區(qū)內(nèi)，較高的VGs能有效減小邊界層內(nèi)壓力的前傳，h=0.8δ時(shí)，在拐角下游過(guò)中心線A處壁面壓力的峰值越高，而h=0.2δ時(shí)，過(guò)中心線A、C處壁面壓力分布相當(dāng)且無(wú)明顯峰值出現(xiàn)。流向渦無(wú)量綱環(huán)量也隨著h的增大而增大，相較其他因素其幅度變化也最大，如圖 14(b)所示。

對(duì)比不同相向旋轉(zhuǎn)葉片間距(η)VGs (Ct2、Ct3和Ct4) 的控制效果。圖12表明，η越大Ls減小幅度越大，Lr減小幅度反而越小，總長(zhǎng)度L減小幅度越大。控制效果較好的是η=6h，Ls減小了42.04%，Lr減小了65.49%，L減小了50.65%。圖13表明，系統(tǒng)阻力隨η的增大而增大。增大η，壁面壓力在轉(zhuǎn)折點(diǎn)前略減小，轉(zhuǎn)折點(diǎn)后略增大，減小了邊界層內(nèi)壓力的前傳，改善了分離區(qū)的壓力分布，同時(shí)流向渦無(wú)量綱環(huán)量也隨之增大，η=6h時(shí)，Г增幅略大，原因可能是減小了流向渦對(duì)間的干擾，如圖 14(c)所示。

對(duì)比不同同向旋轉(zhuǎn)葉片間距(λ)的VGs (Ct2、Ct5和Ct6)的控制效果。圖 12表明，λ越大，Ls和Lr減小幅度均越小。控制效果較好的VGs排列是λ=8h，Ls減小率可達(dá)43.04%，Lr減小率可達(dá)70.55%，總長(zhǎng)度減小了53.13%。圖13表明，系統(tǒng)阻力隨λ的增大而減小。增大λ，壁面壓力在轉(zhuǎn)折點(diǎn)前略增大，轉(zhuǎn)折點(diǎn)后略減小，不利于改善分離區(qū)的壓力分布，同時(shí)流向渦無(wú)量綱環(huán)量也隨之減小，但減幅不明顯，如圖 14(d)所示。

5 結(jié) 論

本文采用數(shù)值模擬的方法，研究了梯形葉片式渦流發(fā)生器對(duì)超聲速壓縮拐角邊界層分離控制的效果。從分離區(qū)平均長(zhǎng)度和系統(tǒng)阻力的變化著手，結(jié)合壁面壓力分布及流向渦環(huán)量的大小，客觀評(píng)價(jià)了渦流發(fā)生器的擺放方式及葉片的幾何參數(shù)對(duì)于邊界層分離控制效果的影響規(guī)律，結(jié)論如下：

1) 葉片式渦流發(fā)生器將轉(zhuǎn)角處的二維分離轉(zhuǎn)變?yōu)槿S的分離流動(dòng)，降低了分離區(qū)內(nèi)壁面壓力，同時(shí)減小了分離區(qū)長(zhǎng)度。

2) 在上游葉片式渦流發(fā)生器作用下，流向渦是直接影響拐角處邊界層分離的原因，流向渦強(qiáng)度越大控制效果越好。高度對(duì)葉片式渦流發(fā)生器誘發(fā)的流向渦強(qiáng)度起主要作用，異向與同向葉片間距的影響較小。

3) 相對(duì)于相向旋轉(zhuǎn)方式，同向旋轉(zhuǎn)葉片式渦流發(fā)生器減小了邊界層內(nèi)壓力的前傳，更利于改善分離區(qū)內(nèi)的壓力分布，分離區(qū)總長(zhǎng)度的減小量與相向旋轉(zhuǎn)方式相當(dāng)，但分離點(diǎn)距轉(zhuǎn)折處平均長(zhǎng)度更短。系統(tǒng)的阻力增量也較相向旋轉(zhuǎn)方式的小。

4) 對(duì)于相向旋轉(zhuǎn)葉片式渦流發(fā)生器，后緣高度越高，分離區(qū)長(zhǎng)度越小，后緣高度h=0.4δ時(shí)系統(tǒng)阻力增量最小；相向旋轉(zhuǎn)葉片間距越大，分離區(qū)總長(zhǎng)度越小，系統(tǒng)阻力增量越大；同向旋轉(zhuǎn)葉片間距越大，分離區(qū)總長(zhǎng)度越大，系統(tǒng)阻力增量越小。