基于混沌Gyrator變換與壓縮感知的光學圖像加密算法
(陜西機電職業(yè)技術學院,陜西 寶雞 721001)
0 引言
隨著各國之間的交流日益頻繁,信息安全已成為當前各國的關注焦點,特別是隨著計算機科學技術與互聯(lián)網技術的快速發(fā)展,使得信息被竊取變得越來越容易[1]。而數(shù)字圖像含有很多用戶想要表達的隱秘信息,是當前用戶進行交流的常用介質[2]。但是,當圖像在開放的互聯(lián)網中傳輸時,易被未知攻擊干擾,導致圖像內容被外泄,帶給用戶諸多安全隱患[3]。為了防止數(shù)字圖像信息在互聯(lián)網中遭遇攻擊,保證其真實性,研究人員提出了圖像加密技術,根據(jù)當前的研究成果可知,圖像加密方法主要集中為2類較,一種是基于混沌理論的加密技術[4-6],另外一個是利用光學理論來加密[7-8]。如李春虎等人[4]為了擴大加密算法的密鑰空間,設計了基于斜帳篷混沌映射和Arnold變換的圖像加密方案,首先根據(jù)明文生成密鑰,然后利用斜帳篷混沌映射和Arnold變換對圖像進行加密,該算法引入混沌映射大大增加了密鑰空間,使密文隨機性和抗攻擊性更強。呂群等人[5]為了解決現(xiàn)有的一些圖像加密算法中,存在無法抵御選擇明文攻擊以及加密程度低、效率低等問題,設計了基于混沌系統(tǒng)和動態(tài)S-盒的圖像加密算法,依靠圖像本身進行二維映射變換來改變像素點的位置,完成圖像的置亂,并根據(jù)混沌序列對置亂后的圖像進行分組,再聯(lián)合S盒,完成圖像的擴散。Ye等人[6]為了增強密文的安全性與抵御攻擊能力,通過聯(lián)合波線置換和塊擴散方法,提出了一種新的魯棒加密方案,根據(jù)波浪特性,設計了波線置換技術,并通過二維 Arnold變換,從多個不同的方向來完成像素的置亂,并基于Arnold變換的輸出序列,設計一種新的像素擴散函數(shù),實現(xiàn)置亂圖像的加密,實驗結果驗證了其算法的安全性。雖然基于混沌理論的加密算法能夠改善密文的安全性,在互聯(lián)網中抵御一定的攻擊能力,但是,不管是低維的混沌映射,還是高維的混沌系統(tǒng),二者均存在迭代周期性,使得密文的安全性不佳[7]。
為了克服基于混沌理論的加密方案存在的不足,學者們又提出了光學加密方法,如肖寧等人[1]為了消除密文的輪廓顯示問題,設計了基于圓諧分量展開與Gyrator變換域相位檢索的光學圖像加密算法,基于離軸圓諧分量展開機制,將Gyrator變換頻譜分割為零階圓諧分量與非零階圓諧分量,并利用球面相位因子來調制零階圓諧分量,輸出加密密文,隨后,引入迭代相位檢索Gyrator變換算法,對非零階圓諧分量完成編碼,輸出最終的密文,實驗結果驗證了其算法的合理性。楊建新等人[7]為了解決當前基于干涉原理的光學圖像加密算法因存在輪廓顯現(xiàn)導致其安全性不高的問題,設計了雙光束疊加與差異模的光學圖像加密算法,基于Gyrator變換,將明文變成一個Gyrator頻域的復雜函數(shù),隨后引入矢量分解方法,將Gyrator頻域復雜函數(shù)進行差異分解,輸出幅度與相位不均等的2個矢量成分,利用2個相位掩碼對矢量成分進行調制,將其從頻域變?yōu)榭沼?將其相位部分視為私密,而幅度部分視為最終加密密文。Wang等人[8]為了增強密文的安全性,消除對稱加密方法的不足,提出了基于改進的幅度-相位恢復機制的非對稱光學圖像加密技術,通過利用不同的初始條件迭代Logistic映射,輸出2個混沌掩碼,將二者作為公共密鑰,隨后,對幅度-相位檢索方法進行改進,完成圖像的加密,獲取一個實值密文,便于存儲與管理,測試數(shù)據(jù)表明了其加密方法的可靠性。
但是,上述光學加密技術均忽略了明文自身的特性,使其低于明文攻擊能力不佳,對此,本文基于混沌Gyrator變換與壓縮感知的光學圖像加密算法。為了增強算法與明文的聯(lián)系,本文利用明文像素來迭代Logistic映射,利用其輸出的混沌序列來生成壓縮感知的測量矩陣;同時,為了降低密文的數(shù)據(jù)容量,引入壓縮感知理論,對明文進行數(shù)據(jù)降維處理,得到一個緊湊的中間密文;最后,根據(jù)明文像素迭代logistic映射的數(shù)組來計算Gyrator變換的旋轉角度,并結合隨機相位掩碼,利用Gyrator變換方法對中間密文完成光學調制,得到最終密文。租后,測試了所提光學加密技術的安全性。
1 壓縮感知[9-10]
隨著信息時代的到來,人們對信息需求量越來越大,使得信號采樣率、傳輸和存儲實現(xiàn)的壓力越來越大[9]。而壓縮感知CS(Compressed Sensing)在采樣方面有獨特的優(yōu)勢,它可以利用比Nyquist采樣理論更少的樣本來重建信號。為了確保重建成功,信號應該是稀疏的或可壓縮的[10],對于一維信號x∈RN,其可以表示為:
(1)
其中:ξ代表N×1維向量的加權系數(shù);φ是一個正交變換矩陣;φi是φ的正交基。
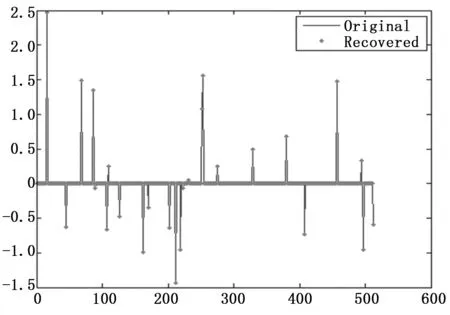
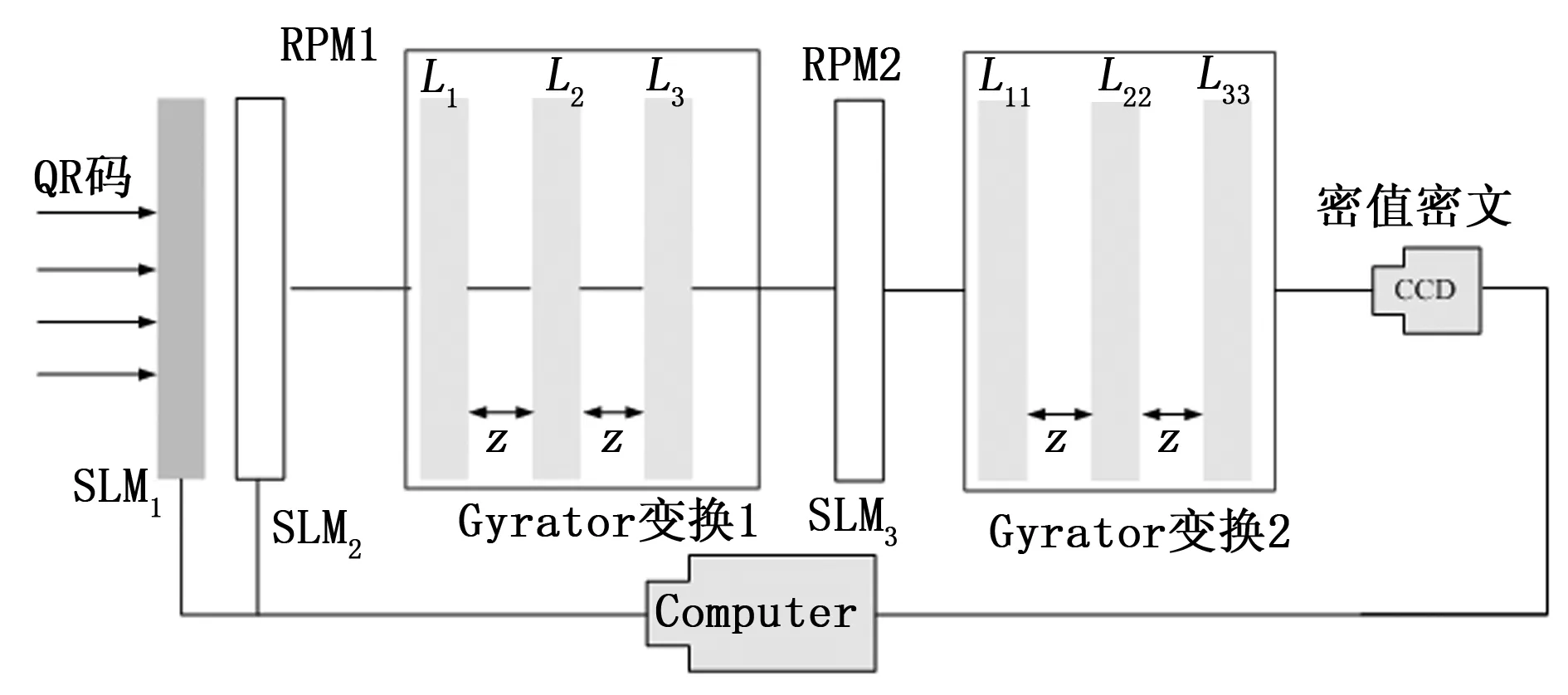
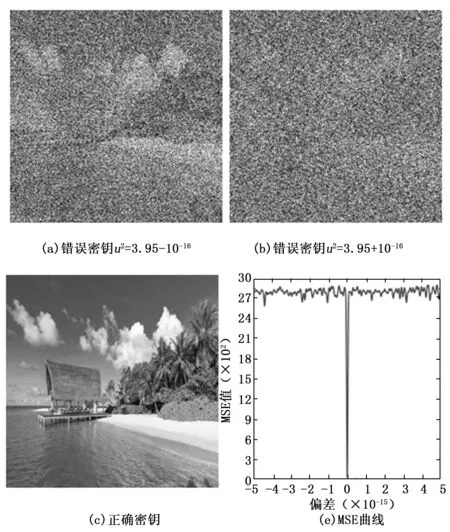
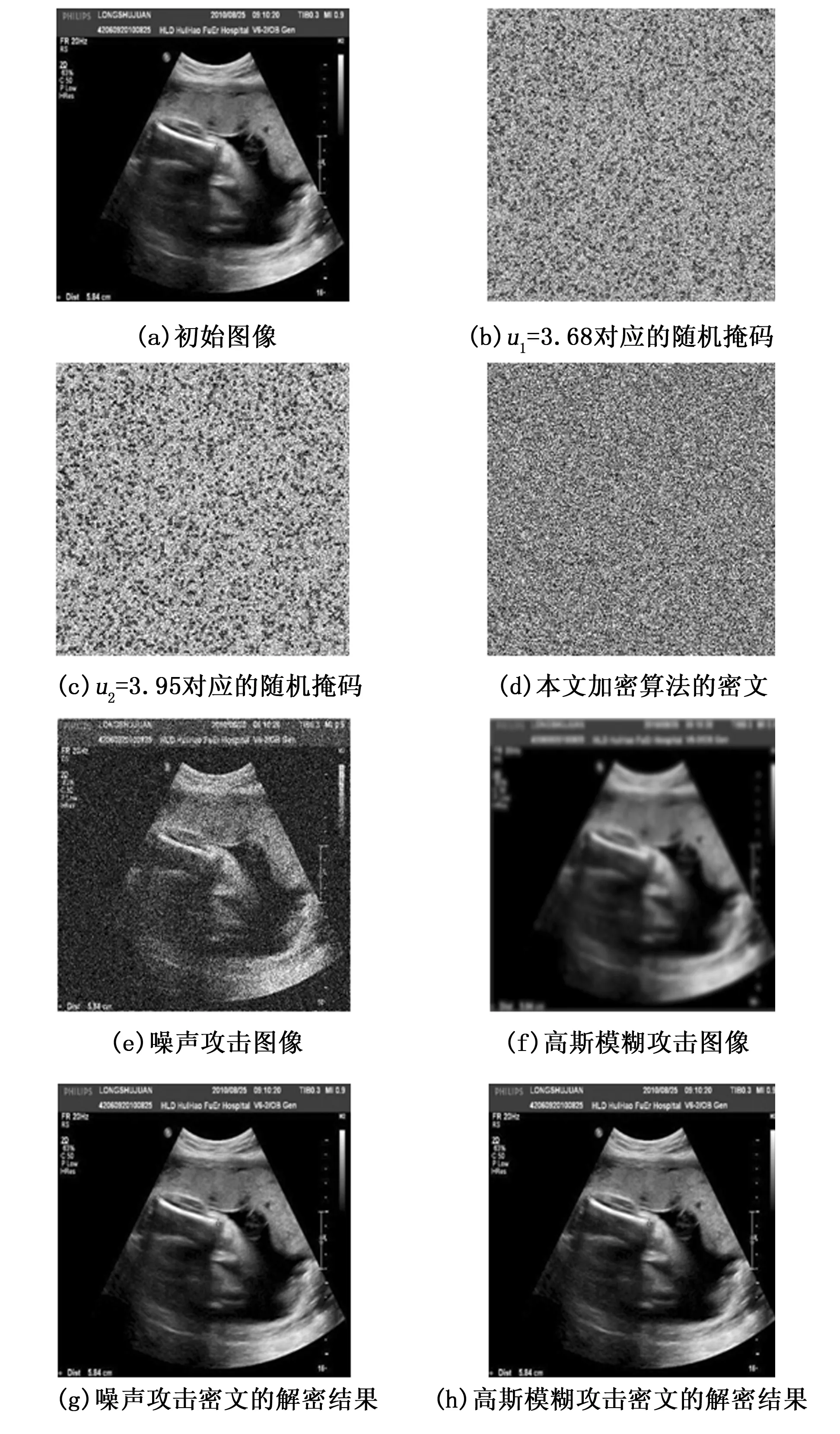
在式(1)中,若ξ只存在K(K< y=φφξ=Θξ (2) 其中:φ是一個M×N維的測量矩陣,它與φ無關。 為了正確恢復ξ,重構矩陣Θ應滿足K的嚴格等距性質: (3) 其中:δK∈[0 1]是等距常量。 最后,通過求解以下非凸優(yōu)化問題,可以以較高的概率恢復原始信號: (4) 取信號商都512,稀疏度為25%,測量長度為5×5,且頻域稀疏為零時,信號的重構效果見圖1。依圖可知,CS的信號恢復準確度較為理想,與初始信號曲線的擬合度較高。 圖1 CS的信號恢復測試 積分變換[1]由于其含有變換參數(shù),可以被視為加密鑰,有效擴大密鑰空間,在圖像加密中得到廣泛應用。若變換角度為α,則圖像fi(xi,yi)的Gyrator變換為[1]: O(x0,y0)=Gα[fi(xi,yi)](x0,y0)= (5) 式中,gα()是Gyrator變換算子;(x,y)為輸入坐標;(u,v)為輸出坐標;o(x,y)是復雜場函數(shù)。 另外,gα()的逆變換|o0|為: g-α(o(x,y))=g2π-α(o(x,y)) (6) (7) 初始圖像經過P1與GT系統(tǒng)后,輸出的編碼結果在P2中: ?o(x,y)exp (8) 其中:λ是光波波長。 圖2 Gyrator變換的光學系統(tǒng) 所提的基于混沌Gyrator變換與壓縮感知的光學圖像加密算法主要包括3個過程:(1)利用Logistic映射來形成測量矩陣;(2)基于壓縮感知的明文預處理;(3)基于混沌Gyrator變換的圖像加密。具體過程如下: 1)令初始明文圖像為f(x,y),其尺寸為h×l;隨后,引入Logistic映射,對其迭代,以形成隨機序列x={x1,x2,...xh×l}: xn+1=μxn(1-xn) (9) 其中:μ∈[0,4]是混沌行為控制參數(shù);xn∈[0,1]、x0分別是輸出值與初始值。 為了增強密文的抗明文攻擊能力,本文利用明文像素來計算Logistic映射的x0: (10) 其中:T是明文的像素數(shù)量。 2)根據(jù)x0與μ1,對式(9)完成迭代,形成隨機序列x={x1,x2,...xh×l}。并將x={x1,x2,...xh×l}排列為一個矩陣,將其作為測量矩陣φ: (11) 3)根據(jù)式(11)的測量矩陣φ,基于“1壓縮感知”,對圖像f(x,y)進行壓縮,獲取預處理圖像fCS(x,y); (12) (13) 6)根據(jù)參數(shù)α1,α2,以及混沌掩碼RPM1、RPM2,根據(jù)圖3所示的光電混合裝置,對預處理圖像fCS(x,y)完成2級Gyrator變換,輸出密文C(x′,y′): C(x′,y′)=Gα1{Gα2{fCS(x,y)×RPM1}×RPM2} (14) 圖3 所提算法的光電混合結構 為了測試本文加密方法的安全性與抗明文攻擊能力,借助Matlab 6.5軟件完成實驗,同時,將當前較為先進的光學加密方案作為對照組:文獻[1]與文獻[7],以突出所提技術的優(yōu)勢。進行實驗的參數(shù)為:光學波長λ=623.8 nm,混沌參數(shù)u1=3.68,u2=3.95,焦距z=0.5 m。 將圖4(a)視為本次實驗的對象,其尺寸為256×256,隨后,基于所提技術、文獻[1]以及文獻[7]對其完成光學加密,結果見圖4(b)~4(e)。依據(jù)測試結果可知,文獻[1]的輸出結果與所提算法、文獻[7]不同,其輸出2個密文,而本文算法與文獻[7]均為一個密文;而且三種技術的加密效果都比較好,明文信息得到了很好的隱藏,非法用戶難以從中直接獲取相關線索。 主觀評估難以具體量化三者的優(yōu)劣,為此,本文引入信息熵值[1]來評估,測試數(shù)據(jù)見表1。根據(jù)表中數(shù)據(jù)可知,文獻[1]的密熵值最高,分別為7.995 2、7.996 7,而本文算法密文熵值略低于文獻[1],約為7.996 1,文獻[7]的密文熵值最低,約為7.993 7。原因是文獻[1]利用了離軸圓諧分量展開機制將Gyrator變換頻譜分割為零階、非零階圓諧分量,并利用球面相位因子,對零階圓諧分量進行調制,形成相應的密文,充分破壞了加密系統(tǒng)的線性關系,將兩個密文分發(fā)給兩個不同的用戶,使其安全性最高。而本文算法則是利用明文像素來計算Gyrator變換的旋轉角度以及相應的相位掩碼,對明文進行二級Gyrator變換加密,顯著增強了密文與明文的關系,充分消除了加密系統(tǒng)的線性特征,使其具備較高的安全性。而文獻[7]則是利用矢量分解方法將Gyrtor頻譜分割為兩個不同的成分,通過2個相位掩碼對矢量成分進行調制,從而完成加密,雖然矢量分解能夠破壞系統(tǒng)的線性關系,但是其結果僅保留在一個純POS掩碼中,使其安全性較低。 圖4 不同算法的光學加密結果 表1 密文熵值的測試果 選擇明文攻擊是是當前互聯(lián)網中較為常見的攻擊類型,對密文安全威脅較大,因此,優(yōu)異的加密技術應可充分抵御選擇明文攻擊[2]。根據(jù)當前的研究成果可知,NPCR、UACI曲線[2]是衡量加密技術的抗選擇明文攻擊能力的經典指標。由文獻[2]可知,NPCR,UACI函數(shù)為: (15) (16) (17) 式中,W,H分別是初始圖像的高度與寬度;I,I′分別代表兩個明文經加密處理后的兩個密文,且這兩個明文都只存在一個相異灰度值[2]。 以圖4(a)為對象,將其 (126, 12)處的像素值212改為21,剩余像素不變,并通過本文算法,文獻[1]和文獻[7]對篡改前后的明文完成加密,根據(jù)式(15)~ 式(16),形成3種方案的NPCR、UACI曲線,結果見圖5。按照輸出的測試數(shù)據(jù)可知,本文光學加密算法的的抗明文攻擊能力最強,其穩(wěn)定的密文NPCR、UACI值都是最大的,分別為99.81%, 35.79%,而文獻[1]、文獻[7]兩種技術的抗選擇明文攻擊能力較弱,對應的NPCR、UACI值均要小于本文算法。主要是因為本文光學加密過程均與明文緊密相連,使其對于不同的初始圖像,會得到不同的加密密鑰,導致其難以獲取正確密鑰,無法對密文進行破譯,本文方案利用初始圖像的像素來迭代Logistic映射,根據(jù)去輸出的隨機序列來壓縮初始圖像,已經計算二級Gyrator變換的兩個旋轉角度,當攻擊者利用其它圖像來攻擊時,因著明文的不同,使得攻擊者得到的密鑰均為錯誤的。而文獻[1]、文獻[7]兩種技術的加密過程均沒有考慮明文自身特性,使其加密密鑰對明文不敏感。 圖5 三種算法的抗選擇明文攻擊能力測試 良好的加密算法應滿足嚴格的“雪崩效應”,即使密鑰發(fā)生極其微小的變化,攻擊者也是無法得到正確的解密圖像[1]。對此,本文驗證了混沌控制參數(shù)u2=3.95的敏感性,通過一個偏差Δt=10-16對u2=3.95進行修改,形成兩個錯誤的密鑰u2=3.95-10-16和u2=3.95+10-16,剩余的密鑰均不變。再借助正確密鑰以及兩組錯誤密鑰來復原圖4(b),輸出結果和對應的MSE曲線如圖6所示。根據(jù)測試數(shù)據(jù)可知,即使u2=3.95發(fā)生了10-16這樣極其微小的修改,仍然是不能對密文進行破譯。只有當密鑰沒有偏差時,才能正確破譯密文,此時的MSE曲線出現(xiàn)突變,其值接近零。這說明所提光學加密技術具備強烈的密鑰敏感性。 圖6 所提算法的密鑰敏感性測試 醫(yī)學圖像對于醫(yī)生判斷病情至關重要,若圖像在網絡傳輸中遭受攻擊,則會嚴重影響圖像的質量,對于病情的判斷不利。為此,本文以B超圖像為例,其尺寸為256×256,見圖7(a);根據(jù)式(10)可計算初值x0=0.65;設置u1=3.68,u2=3.95,根據(jù)算法過程,可得到Gyrator變換的兩個旋轉角度α1=0.51°,α2=0.63°。依據(jù)式(13),得到的兩個隨機掩碼分別見圖7(b)和圖7(c)。再設置光學變換參數(shù):光學波長λ=623.8 nm,混沌參數(shù)u1=3.68,u2=3.95,焦距z=0.5 m。根據(jù)式(14),獲取相應的密文,見圖7(d)。 若圖7(a)在網絡中遭遇噪聲與模糊攻擊,見圖7(e)和圖7(f),嚴重降低了圖像質量,給醫(yī)生的準確判斷病情帶來不利影響。但是,若本文算法的密文遇到噪聲與模糊攻擊后,根據(jù)所以算法的密鑰,對其復原,結果見圖7(g)和圖7(h)。由圖可知,所提算法充分混淆了醫(yī)學圖像信息,即使其在網絡中遇到噪聲與模糊攻擊,其影響的也只是加密密文而已,只要用戶利用正確的密鑰對其解密,既可獲得清晰完整的圖像。 圖7 所提算法的實際應用測試 為了提高加密算法對初始明文的敏感性,增強密文的抗選擇明文攻擊能力,本文設計了混沌Gyrator變換耦合壓縮感知的光學圖像加密算法。通過明文像素來迭代Logistic映射,利用其輸出的混沌序列來生成壓縮感知的測量矩陣;并根據(jù)測量矩陣,利用壓縮感知技術對明文進行預處理,增強算法與明文的關系,有效降低密文的數(shù)據(jù)容量;最后,利用兩個不同的隨機序列來計算Gyrator變換的兩個旋轉角度,結合相位掩碼,對預處理結果完成二級光學調制,完成圖像的加密。所提算法不僅有效破壞了整個密文的線性特性,而且對明文十分敏感。測試結果驗證了所提光學加密技術的安全性。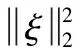
2 Gyrator變換
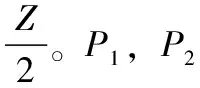
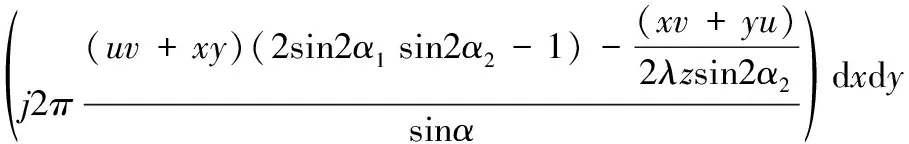
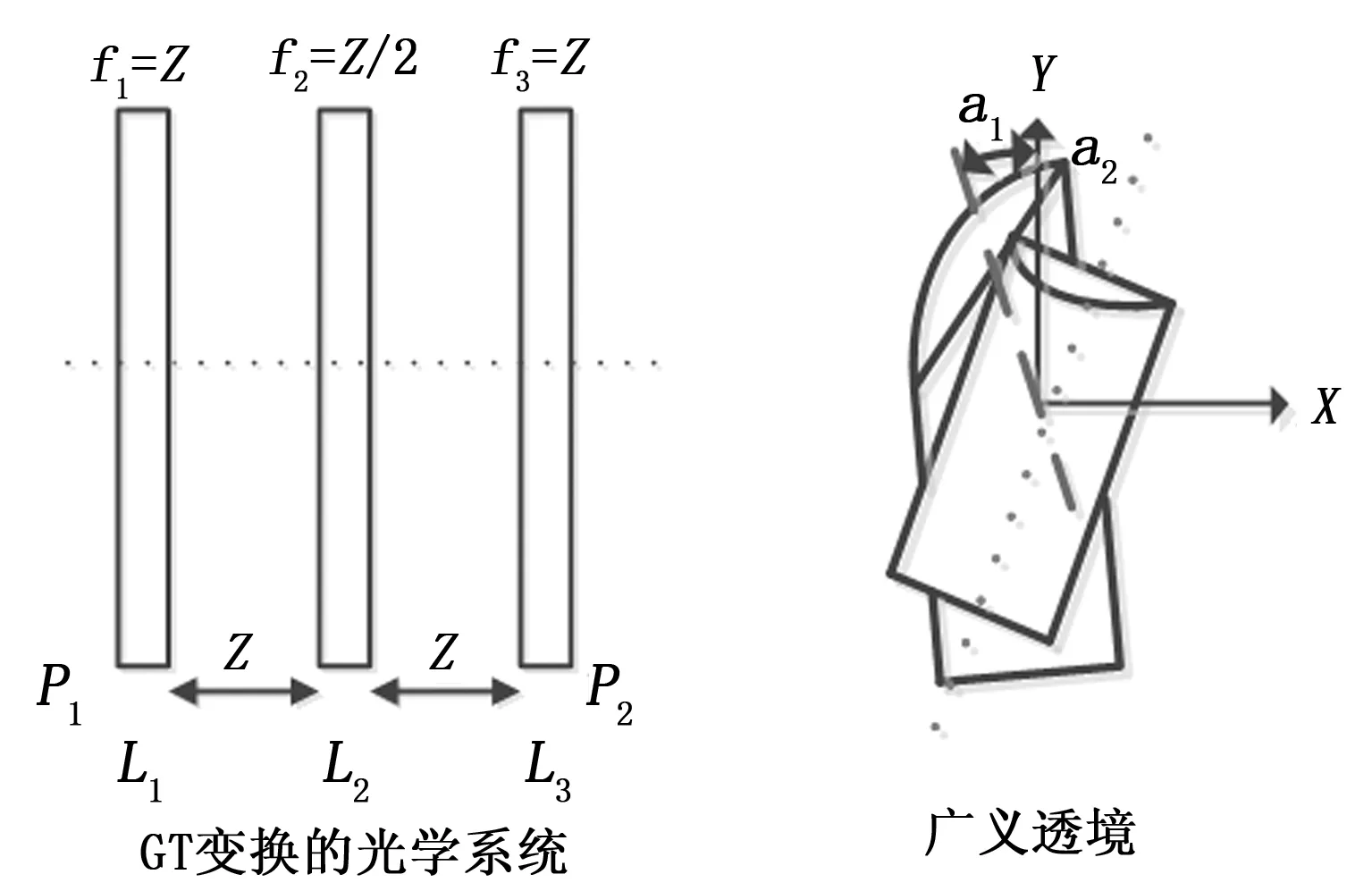
3 本文光學圖像加密算法
4 實驗結果與分析
4.1 光學圖像加密效果


4.2 抗選擇明文攻擊能力測試
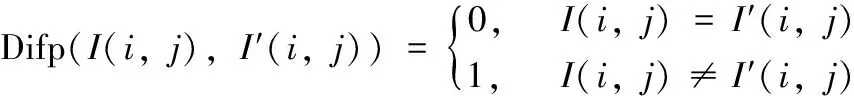
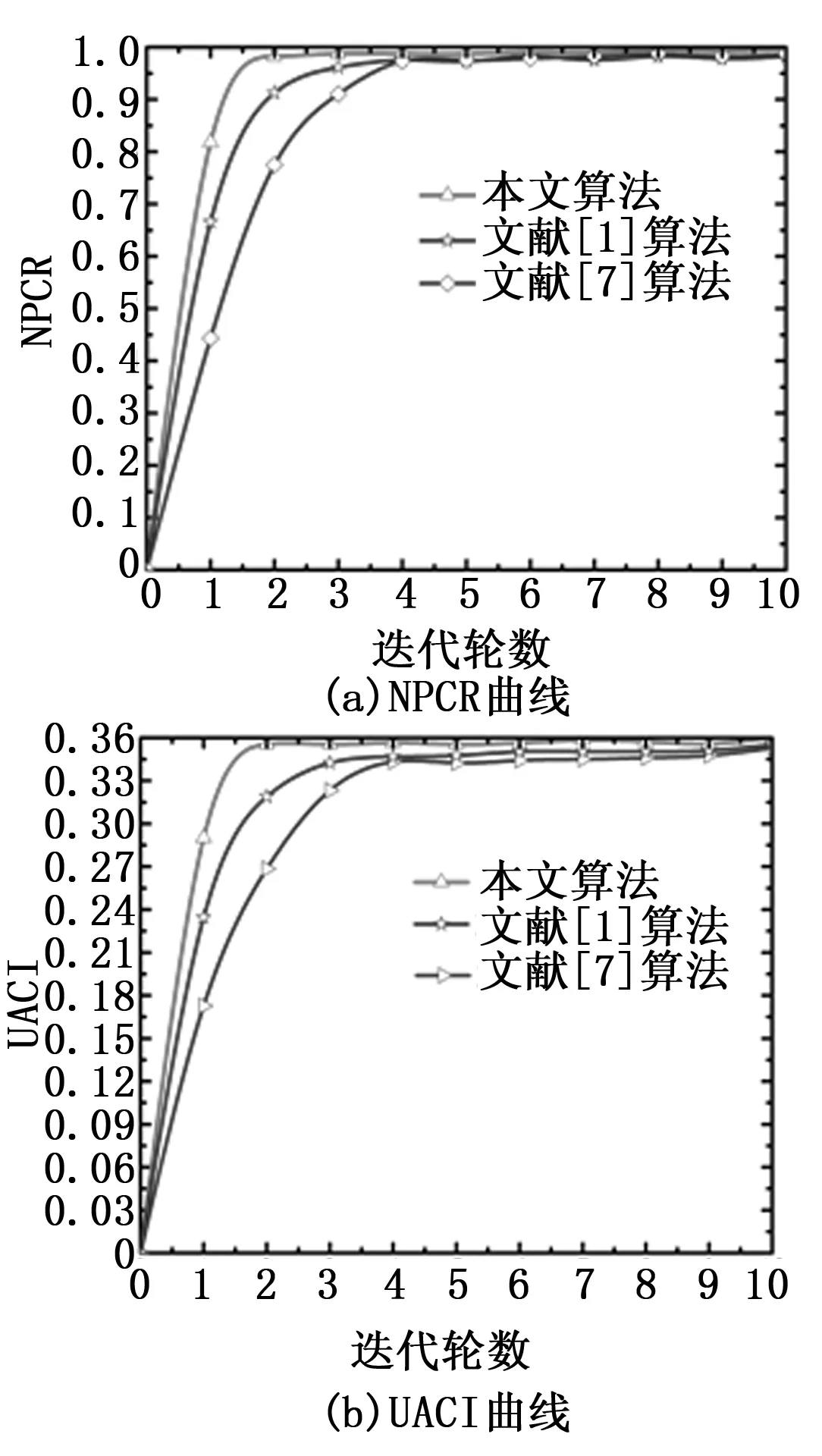
4.3 密鑰敏感性測試
4.4 加密算法的實際應用
5 結論

