基于KPCA-DFNN海洋微生物發酵過程軟測量建模

，，，

(1.蘇州工業園區職業技術學院，江蘇 蘇州 215123；2.江蘇大學 電氣信息工程學院，江蘇 鎮江 212013)

0 引言

海洋微生物作為微生物的一類，因其生存的海洋具有特殊的環境，故其所產生的酶與其他微生物所產生的酶相比具有更加獨特的性質，如耐低溫，耐堿性，PH作用范圍寬等，這使得海洋微生物在食品加工、酶工業、添加劑和醫藥等發酵行業具有極大的開發潛力和應用前景[1-5]。在海洋微生物發酵過程中，為保證發酵產物的品質和質量，需要實時檢測一系列生物參數，尤其是基質濃度、菌體濃度及產物濃度(酶活)。當前，在線測量儀器僅能檢測發酵過程中某些物理和化學參數，還沒有成熟實用的儀器來測量這些關鍵生物參數[6-8]。在此背景下，許多關于微生物發酵過程中生物參數的軟測量方法應運而生，其中，基于神經網絡[9]的預測方法成為軟測量領域的研究熱點。然而，對于海洋微生物發酵過程這一類十分復雜的非線性系統來說，如果沒有先驗知識，就盲目應用神經網絡方法，關鍵生物參數的測量問題就不能很好的解決。為此，文中將核主元分析法(Kernel Principal Component Analysis，KPCA)[10-12]和動態模糊神經網絡(Dynamic Fuzzy Neural Network，D-FNN)[13-15]相結合，提出了一種基于KPCA-DFNN的軟測量方法。

以典型的海洋微生物-海洋蛋白酶發酵過程為研究對象，首先，確定基質濃度、菌體濃度、相對酶活(能夠更好地描述酶活的變化趨勢)這三個參量為軟測量模型的輸出變量，環境變量為模型的初始輸入變量。然后，利用KPCA對輸入變量進行數據壓縮和信息抽取，將所提取的主元作為DFNN的輸入，以上三個變量作為DFNN的輸出，建立了基于KPCA-DFNN的海洋蛋白酶發酵過程生物參量軟測量模型。仿真結果表明，該模型較基于DFNN和PCA- DFNN建模具有學習速度快、預測精度高等優勢，有益于海洋蛋白酶的高效、高質量生產。

1 核主元分析與動態模糊神經網絡的原理

1.1 核主元分析

核主元分析是主元分析法(Principal Component Analysis，PCA)的非線性推廣，其具體算法如下：

給定n個樣本，樣本集X={x1,x2,…,xn}，xk∈Rm，由非線性函數φ(·)將輸入數據從原空間映射到高維特征空間F，F中的樣本記為φ(xk)，且滿足：

(1)

在F空間中樣本的協方差矩陣C為

(2)

對C進行特征值分解

λV=CV

(3)

式中，V是與λ對應的特征向量，特征值λ≥0。將(3)式的兩邊左乘以核樣本φ(xk)：

λφ(xk)·V=φ(xk)·CV，k=1,2,…,n

(4)

解方程可得與非零特征值對應的特征向量V。其解一定處于φ(x1),φ(x2),···,φ(xn)張成的空間中，所以V可以表示為：

(5)

其中，

φ(x)=[φ(x1),φ(x2),…,φ(xn)]，α表示a1,…,an中的一個列向量。

引入核函數：

Kij=K(xi,xj)=[φ(xi),φ(xj)],i,j=1,2,…,n

(6)

nλα=Kα

(7)

歸一化特征向量V，即(V,V)=1，即可得樣本x在特征空間中的第k(k=1,2,…,n)個主元分量tk(x)：

(8)

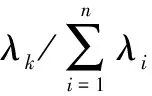
(9)

式(9)表示前p個λk的和與總和比值大于E，通常選取E>85%。

(10)

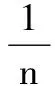
1.2 動態模糊神經網絡

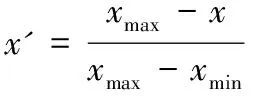
第1層：輸入層，每個節點代表一個輸入變量。

第2層：隸屬函數層，每個節點代表一個隸屬函數，該隸屬函數可用式(11)表示：

(11)

其中，i=1,2,…,r,j=1,2,…,u，r是輸入變量數，u是隸屬函數的數量，即系統的總規則數，cij和σj分別是xi的第j個高斯隸屬函數的中心和寬度，xmin是xi的第j個高斯隸屬函數。

第3層：T-范數層，每個節點代表一個可能的模糊規則中的IF-部分，即該層的節點數反映了模糊規則數。第j個規則Rj的輸出為：

(12)

其中：j=1,2,…,u，X=(x1,x2,...,xr)∈Rr，Cj=(c1j,...,crj)∈Rr是第j個RBF單元的中心。

第4層：歸一化層，這些節點被稱為N節點。其數目等于模糊規則的節點數。第j個節點Nj的輸出為：

(13)

第5層：輸出層，每個節點代表一個輸出量，此輸出是所有輸入信號的疊加：

(14)

式中，wk是THEN-部分或者稱為第k個規則的連接權，wk=ak0+ak1x1+…akrxr,k=1,2,…u，y是變量的輸出。

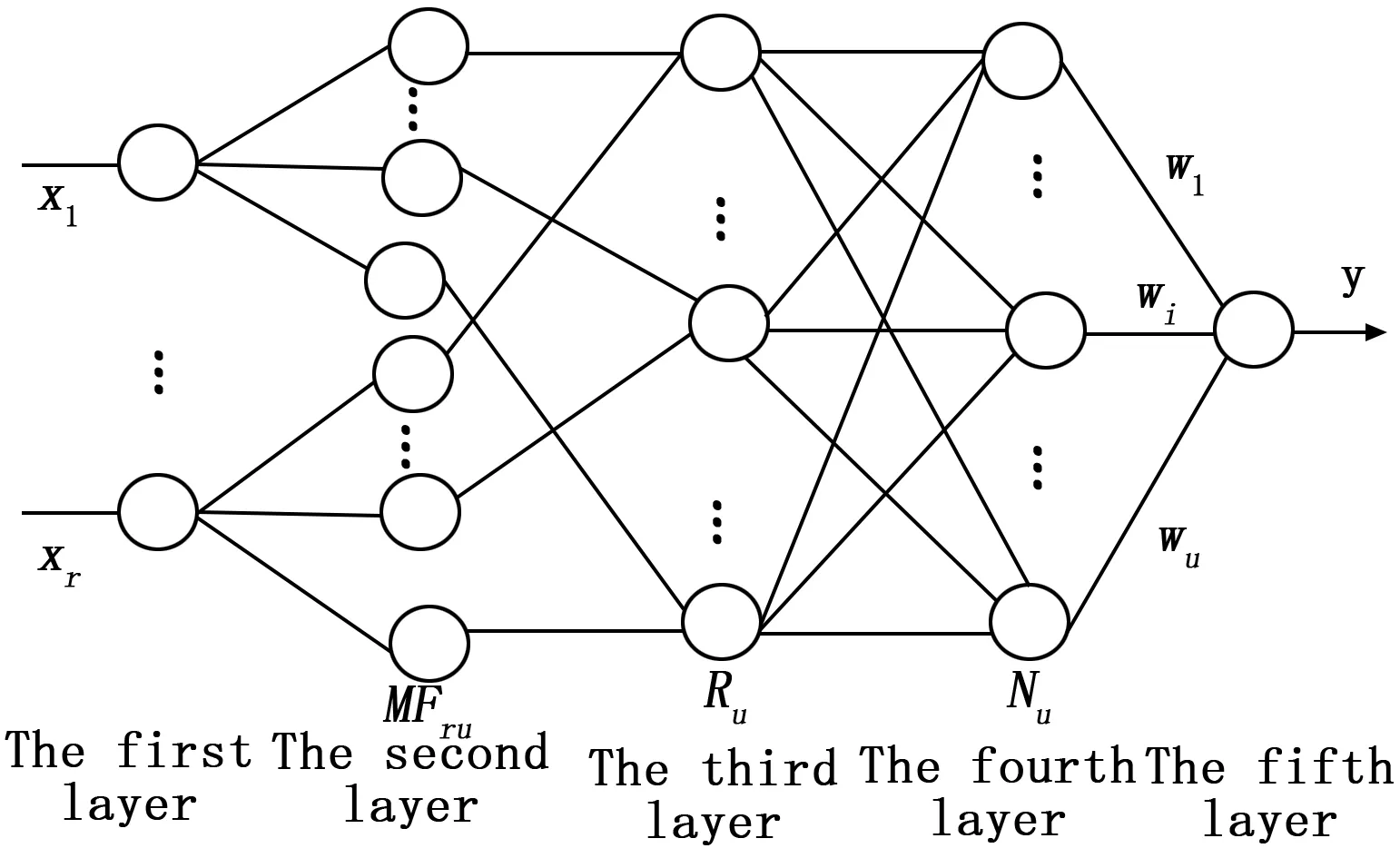
圖1 DFNN的結構圖

2 KPCA-DFNN模型的構建與驗證

2.1 模型的構建

基質濃度S、菌體濃度X、相對酶活P對海洋蛋白酶發酵過程的優化控制非常重要，因此，選擇這三個變量作為KPCA-DFNN軟測量模型的輸出變量。通過分析海洋蛋白酶發酵機理并結合發酵過程的實驗數據，選取了10個影響生物參數S、X、P的主要因素作為初始樣本變量，分別是：時間t、溫度T、攪拌速度r、溶解氧濃度DO、空氣流量l、pH值、CO2濃度、基質進給速率u、發酵罐壓力p、反應器體積v。

采集了10批發酵數據，前9批作為模型的訓練樣本集，第10批作為模型的測試樣本集，由于采集到的樣本數據變化范圍較大，如果直接使用原始測量數據進行計算，不僅會夸大量綱數據的作用，而且還可能導致信息丟失或引起數值計算的不穩定。需要對樣本數據進行歸一化處理。公式如下：

(15)

式中：xmax為樣本數據的最大值，xmin為樣本數據的最小值，x為原始樣本數據，x′為歸一化后的數據。歸一化后樣本數據在[0，1]之間。

根據核主元分析法和動態模糊神經網絡的基本原理，構建了基于KPCA-DFNN的海洋蛋白酶發酵過程生物參量的軟測量模型，建模過程如圖2所示。建模步驟如下。

步驟1：根據建模對象選取適當的輸入輸出樣本數據。

步驟2：利用式(15)對輸入輸出數據進行預處理。

步驟3：根據KPCA算法對輸入變量進行數據壓縮和信息抽取，消除輸入變量之間的相關性，進行特征選取。文中按累積方差百分比大于95% ，KPCA選定了2 個特征主元，PCA選定了6個特征主元。

步驟4：將提取非線性主元作為DFNN的輸入，X、S、P作為模型的輸出變量，利用訓練樣本集對DFNN模型進行訓練，選取最佳模型構建參數。

步驟5：利用測試樣本集對建好的KPCA-DFNN軟測量模型進行驗證。

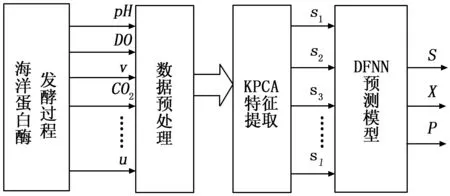
圖2 海洋蛋白酶發酵過程預測模型框圖

2.2 模型驗證

用測試樣本集對建好的KPCA-DFNN模型進行仿真驗證。仿真結果如圖3、圖4和表2所示。

圖3顯示出了海洋蛋白酶發酵過程X、S、P的離線化驗值(真實值)和軟測量值(預測值)對比結果。

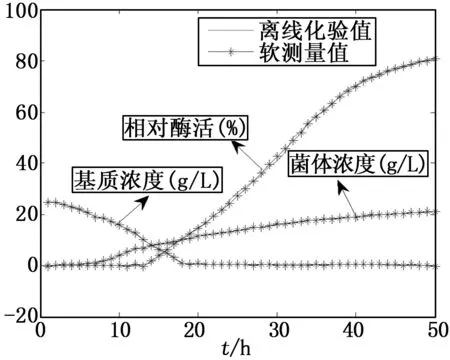
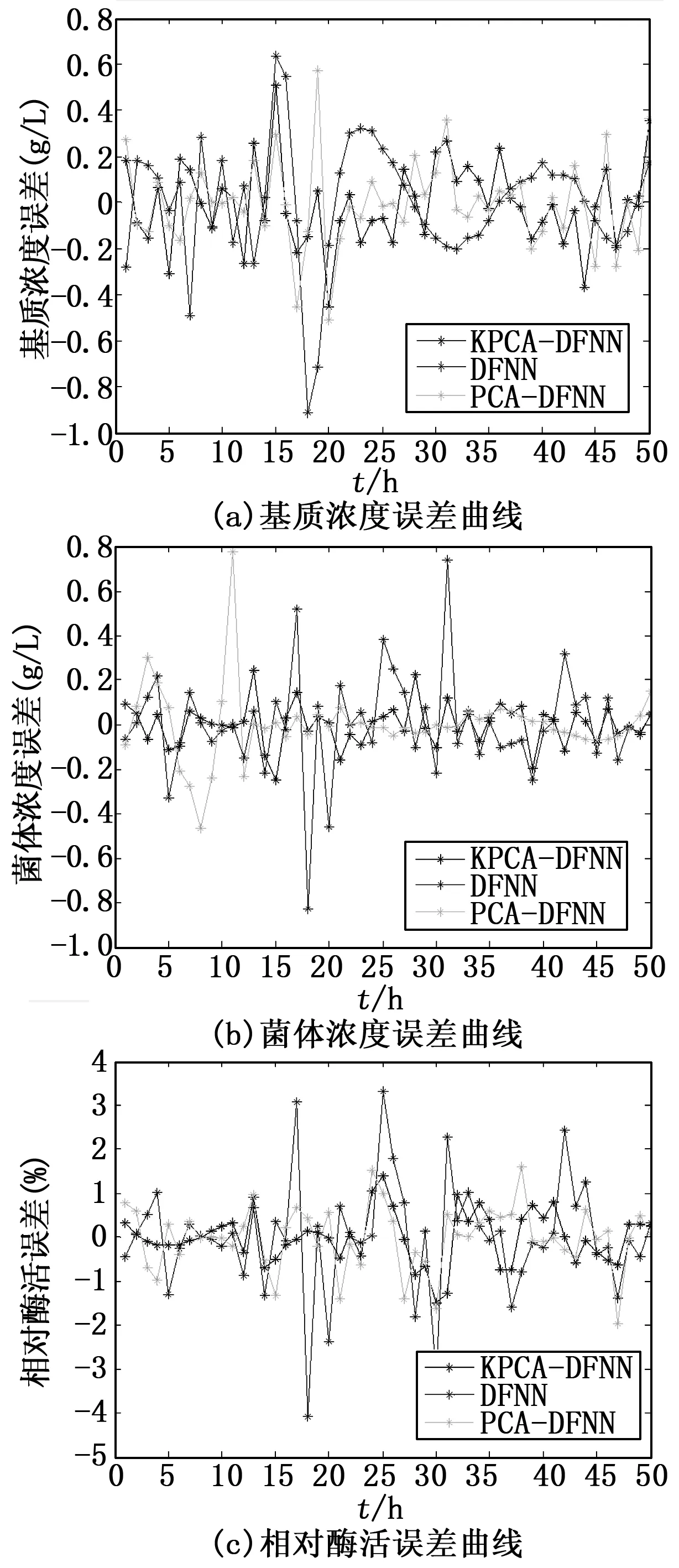
圖3 KPCA-DFNN生物參量預測曲線

圖4 DFNN、PCA-DFNN、KPCA-DFNN生物參量預測值誤差曲線

雖然試驗過程中采集到的樣本值分散性很大和重復性很小，但從圖3中可以看出，對于X、S、P，基于KPCA-DFNN的軟測量模型，輸出的軟測量值都能夠很好的追蹤離線化驗值，這說明，KPCA-DFNN具有較好的逼近能力。

采用均方根誤差(RMSE)和平均絕對誤差(MAD)更直觀的反映DFNN、PCA-DFNN、KPCA-DFNN建模方式的預測效果，如表1所示。

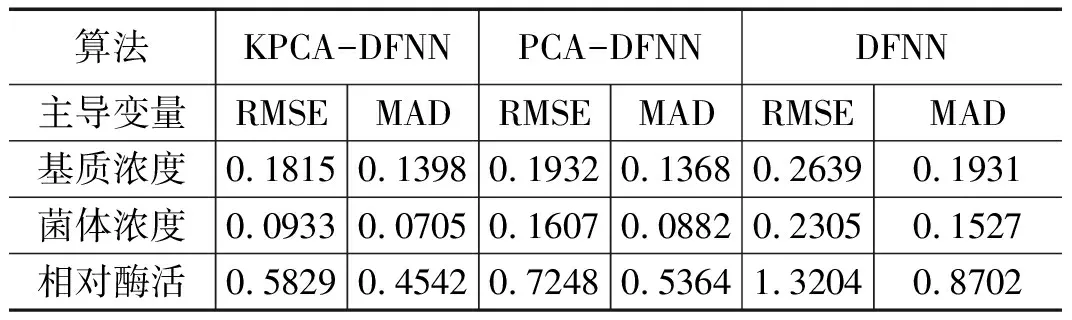
表1 DFNN、PCA-DFNN、KPCA-DFNN預測值誤差對比

(16)

(17)

其中:n是數據對的數目，t(i)和y(i)是第i個期望輸出與實際輸出。

另外，為了更清晰地描述DFNN、PCA-DFNN、KPCA-DFNN的預測能力，圖4中給出了這三種建模方法預測誤差。

從表1和圖4中可以看出，基于KPCA-DFNN的建模所得到基質濃度、菌體濃度和相對酶活的預測誤差要比DFNN和PCA-DFNN小得多，這進一步表明，即使在同樣的訓練數據和測試數據的條件下，KPCA-DFNN的預測效果比DFNN和PCA-DFNN好。既基于KPCA-DFNN在發酵樣本預測中具有顯著的作用。

3 結論

為解決海洋微生物發酵過程中生物參量難以實時在線測量的問題，文中以海洋蛋白酶發酵過程為例，將核主元分析法(KPCA)與動態模糊神經網絡(DFNN)相結合，提出一種基于KPCA-DFNN的建模方法。首先確定了X、S、P作為海洋蛋白酶預測模型的輸出變量，同時，通過對海洋蛋白酶發酵過程進行機理分析，選定了10個影響輸出變量的環境變量作為KPCA-DFNN模型的輸入變量。用訓練樣本集對這些變量進行預處理后，按照累積方差百分比大于95%，KPCA提取了2 個特征主元。根據DFNN算法對提取后的數據進行學習訓練，建立了基于KPCA-DFNN的海洋蛋白酶發酵過程生物參量的軟測量模型，用測試樣本集對模型進行仿真驗證，試驗結果表明與DFNN、PCA-DFNN建模方法相比，所建立的KPCA-DFNN模型具有良好的預測精度，所得生物參量預測值的最大RMSE為0.582 9，最大MAD為0.454 2，滿足發酵過程中生物參量的在線測量要求。