基于熵權Vague 集的多目標決策方法

趙慶慶，黃天民

(西南交通大學數學學院，成都611756)

(*通信作者電子郵箱Zhaoqingswjtu@163．com)

0 引言

1965年，Zadeh［1］首次提出了模糊集的概念，并在管理決策領域［2－3］、軍事運籌學領域［4］、人工智能領域［5］等取得重大進展。1993年，Gau等［6］提出了Vague集理論，它是模糊集的推廣形式，Vague集同時表示了支持和反對的證據以及未知程度，比模糊集向決策者提供了更多的信息。Chen等［7］將Vague集應用于多目標決策問題，通過定義一類計分函數或者加權計分函數得到決策結果，Hong等［8］以及李凡等［9］分別對文獻［7］方法進行分析，針對不足之處給出修改形式。劉華文［10］在此工作的基礎上，提出包含決策者猶豫度的計分函數與加權計分函數，并給出一種距離目標選擇方法。然而在實際操作中，精確地表示一個元素屬于某個集合的程度很難實現，把隸屬程度用區間數表示有更大的靈活性，周珍等［11］和王會英等［12］等利用區間值Vague集對Vague集作了進一步拓展并將其應用于多目標決策領域。

目前的研究成果均在集中Vague集的運算法則、Vague集的相似性度量、方案的優選準則等理論或方法方面，關于目標的Vague值，即隸屬度、非隸屬度和猶豫度的計算沒有相應的研究。王玨等［13］通過設定滿意度下界和不不滿意度上界計算方案的支持目標集，反對目標集和中立目標集確定方案的Vague估計值，最后利用評價函數進行排序，但這種方法主觀性較強并且評價函數單一，當支持目標集和反對目標集相同時無法得出最優方案。為了改進目標權重的主觀任意性，許多學者基于信息熵的理論研究問題，按照熵的思想，人們在決策中獲得的信息的多少和質量是決定決策精度和可靠性的因素之一，所以熵在應用于案例的效果評價時是一個很理想的尺度，適用于確定權重的過程。戴厚平［14］對屬性信息完全未知且屬性值為區間直覺模糊數的多屬性決策問題進行了研究，提出基于信息熵的區間直覺模糊多屬性決策方法。黃松等［15］利用熵權系數法計算權重，并通過專家給出每個目標的滿意度下界和不滿意度上界得出各個目標的平均滿意度下界和不滿度上界，若用此方法對目標過多的方案排序，會增加專家的工作量，降低決策效率。熵權法計算出的目標權重具有客觀性，但是研究者在利用熵權法進行多目標決策時，往往只考慮客觀權重，忽略了人的主觀偏好。

基于以上的問題，本文重新定義了評價函數，并綜合考慮客觀權重和主觀權重得到各個目標的權重向量區間，通過計算方案的支持目標集和反對目標集得到方案的Vague估計值，最后利用新的評價函數進行排序。另外還將該方法與文獻［13］方法作了比較，表明該方法更為合理和有效。

1 預備知識

假設有n個備選方案，m個目標，n個備選方案對m個目標的指標值構成決策矩陣

表示成矩陣的形式為:

多目標決策的一般模型可描述:

其中fij表示方案xj的第i個目標值。

首先將決策矩陣F轉化為目標優屬度矩陣，通常采用如下方法確定目標的優屬度μij:

對于效益型指標(目標值越大越好)

對于成本型指標(目標值越小越好)

對于效益型目標(目標值越接近某一固定值越好)

2 確定各目標的權重向量區間

2．1 熵權法確定目標的客觀權重

熵是系統無序程度的一種度量，目前熵值的表示方法也有很多，一種是基于概率的表示，系統可能處于N種不同的狀態，每種狀態出現的概率為pi(i=1，2，…，N)，則評價該系統的熵可定義為:

或者利用三角函數定義直覺模糊熵，它主要考慮隸屬度與非隸屬度的偏差，設Y是一個論域，且

為X上的直覺模糊集，則xi的熵值定義為:

其中πA(x)=1－uA(x)－vA(x)。

因為要定義各個目標的客觀權重，根據目標的確定性和便于歸一化處理的特點，采用基于概率的方法確定目標的熵值。

定義1［14］第i個目標的熵值表示為:

熵是信息論中衡量不確定性的指標，信息量的分布越趨于一致，不確定性越大，則當μij/μi的值完全相等時，熵Ei的值達到最大:max Ei=ln m。容易看出:目標的信息熵越小，表明目標值的變異程度越大，提供的信息量越大，則其權重也應越大;反之，目標的信息熵越大，表明目標的變異程度越小，提供的信息量越小，則其權重也應越小。

定義2［14］差異程度越大的目標越重要，則可將目標的熵值取補后歸一化處理得到目標i的客觀權重:

各目標的客觀權重向量

2．2 確定目標的權重向量區間

對于綜合考慮客觀權重和主觀權重，人們往往采取線性加權法，這樣會丟失掉一些有用信息，針對這一缺陷本文重新定義了權重區間的概念。

定義3 已知由熵權法得到的客觀權重向量w'=(w1'，w2'，…，wm')，由專家確定的主觀向量 w″=(w1″，w2″，…，wm″)，目標的權重向量區間定義為:

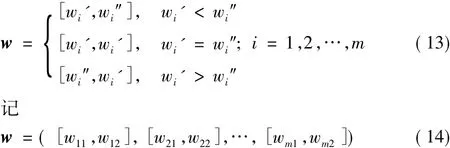
3 Vague估計值和評價函數的確定

3．1 計算方案的Vague估計值

定義 4［13］設 f(x)=(f1(x)，f2(x)，…，fm(x))Τ表示m個目標的向量。

1)令λU是決策者能夠接受的滿意度下界，若μij＞λU，則稱第j個方案支持第i個目標;

2)令λL是決策者能夠接受的不滿意度上界，若μij＜λL，則稱第j個方案反對第i個目標;

3)若λL≤μij≤λU，則稱第j個方案對第i個目標保持中立。

定義 5［13］

1)Fj=為第j個方案的支持目標集;i=1，2，…，m;j=1，2，…，n。

2)Aj=為第j個方案的反對目標集;i=1，2，…，m;j=1，2，…，n。

3)Nj=為第j個方案的中立目標集;i=1，2，…，m;j=1，2，…，n。

一般的，支持目標集中包含的目標越多越好。下面我們利用Vague集的相關理論進行Vague估計。

定義6 設權重區間

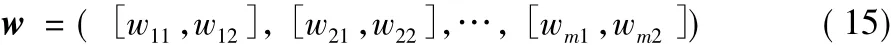
對方案xj∈X，它在m個目標上滿足決策者要求的程度用Vague值V(xj)表示，即V(xj)=［t(xj)，1－f(xj)］，其中:

并且 i=1，2，…，m;j=1，2，…n。

3．2 評價函數的確定

定義7 設V(xj)是一個區間Vague值，V(xj)表示為:

定義評價函數s(xj)為:

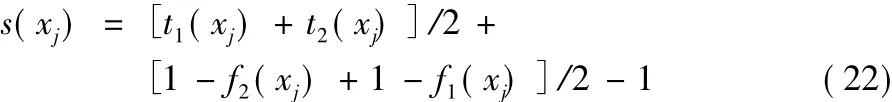
容易看出，s(xj)∈［－1，1］。由上述定義可知，s(xj)的值越大，方案越滿足決策者的要求，進而可以選出最優方案。

3．3 基于熵權Vague集的多目標決策算法

基于對上述理論和方法的分析，下面本文給出基于熵權Vague集的多目標決策方法的具體步驟:

步驟1 將決策矩陣轉化為目標優屬度矩陣;

步驟2 綜合熵權法求得的客觀權重和專家決定的主觀權重轉化為權重向量區間;

步驟3 根據定義求出每個方案的Vague估計值;

步驟4 利用評價函數對所有方案排序并選出最優方案。

4 算例

本文采用文獻［17］的最佳防御要點選擇問題，該問題中有5 個方案，6 個目標，即 X=(x1，x2，x3，x4，x5)，f=(f1，f2，f3，f4，f5，f6)，其中f1為成本型目標，f2為固定性目標，其余均為效益型目標，經過軍事專家和指揮員評判，確定各個目標的權重向量為 w″=(0．24，0．18，0．18，0．12，0．12，0．16)，且決策矩陣如下:

步驟1 將決策矩陣F轉化為目標優屬度矩陣μ為:

步驟2 求出每個目標的權重向量區間。

由熵權法求得每個目標的熵值為:

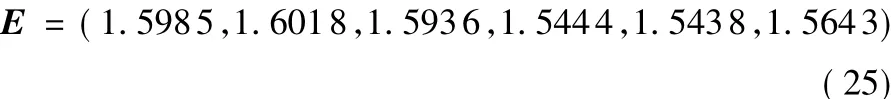
歸一化處理得到各個目標的客觀權重:

根據定義每個目標的權重向量區間為w:

步驟3 求出每個方案的Vague估計值

取 λL=0．75，λU=0．75，則各個方案的支持目標集、反對目標集和中立目標集分別為:

根據定義得到5個方案的Vague估計值:

步驟4 分別計算5個方案的評價函數值

s(x1)=0．011，s(x2)=0．524，s(x3)=0．011，s(x4)=0．643，s(x5)= － 0．194; 則得排序結果為 x4> x2> {x1，x3}>x5，最優方案為x4．按照文獻［13］的排序方法，當λL=0．5;λU=0．75 時得到的排序結果為{x2，x4} > {x1，x3} >x5，并沒有選出最優方案，顯然本文的排序方法更加有效。

容易看出，當λL、λU取不同的值時排序結果不同，表1為不同的λL、λU的排序結果，表2為文獻［13］的排序結果。

表1 本文方案排序結果Tab．1 Ranking result of the proposed scheme

分析表1、表2 的排序結果，當 λL=0．57，λU=0．93 時，本文選出的最優方案為x4，文獻［13］的方法沒有選出最優方案，λL，λU取其他值時，兩種方法的排序結果相同，所以本文的排序方法是合理的并且更加有效;文獻［16］提出一種決策方法，并且計算了 λL=0．57，λU=0．90 時的決策結果，得到的排序方案為x2> x4> x5> x3> x1，當 λL=0．57，λU=0．90時，本文決策方法的排序結果為x4>x2>x1>x3>x5，顯然取 λL=0．57，λU=0．90 時，方案 x4更符合要求，取其他值時兩種方法的決策結果相同，驗證了文中方法更優;文獻［17］是傳統的決策方法，文中方法包含了文獻［17］的方法，當取 λL=0．46，λU=0．93 時，得到的排序結果為 x2> x4>x3>x1>x5，此時的排序結果與文獻［17］的極大極小法相同，決策者持悲觀態度;當取 λL=0．00，λU=0．36 時，得到的排序結果與文獻［17］的極大極大法相同，決策者持樂觀態度。

表2 文獻［13］中方案排序結果Tab．2 Raking result of the scheme in［13］

5 結語

本文提出一種基于熵權Vague集的多目標決策方法，提出權重區間的概念并且重新定義了評價函數，通過計算方案的支持目標集和反對目標集得出方案的Vague估計值，從而實現對方案的排序。本文方法可以兼顧決策者的主觀偏好和客觀信息，使決策結果接近實際情況。并且此決策方法它蘊含了極大極小法和極大極大法，有效避免了目標權重的主觀任意性問題，計算實例表明了此方法的可行性和有效性。但是確定滿意度的上、下界時具有隨機性和任意性，所以滿意度上下界取值問題仍待進一步研究。