例析背景下的解析幾何問題

廣東

劉光明

(作者單位：廣東省汕尾市華南師范大學附屬中學汕尾學校)

廣東

劉光明

一、離心率問題

離心率問題是高考解析幾何中的常見問題，其核心是尋找a與c之間的關系，通常都是根據已知條件構造方程或分別求出a，c的值.

二、直線問題

直線問題無非就是直線斜率或者直線方程的求解，在解析幾何中直線作為與曲線相交的主要角色，常常設直線的點斜式或者斜截式，當然通過幾何圖形分析直線斜率也不失為一種高明之選.

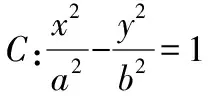
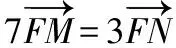
【例題3】(2009·全國卷Ⅱ理·9)已知直線y=k(x+2)(k>0)與拋物線C:y2=8x相交于A,B兩點，F為C的焦點，若|FA|=2|FB|，則k=

( )

【點評】與拋物線焦點相關問題，利用拋物線的定義，借助幾何圖形分析，將數形結合思想融入解題之中.

三、軌跡問題

處理軌跡方程問題常見的方法有直接法、定義法、相關點法、待定系數法等，在解析幾何中軌跡方程作為后續問題的基礎，正確求解方程有著至關重要的作用.

四、弦長問題

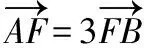
五、取值范圍與最值問題

取值范圍問題在考試中難度要求都不低，首先要將要求范圍的代數表達式求解出來，然后借助不等式或者函數的值域處理，當然特殊值或者特殊圖形對于范圍估計也有一定的幫助. 解析幾何中，圖形上的動點設置條件確定某字母的取值范圍.

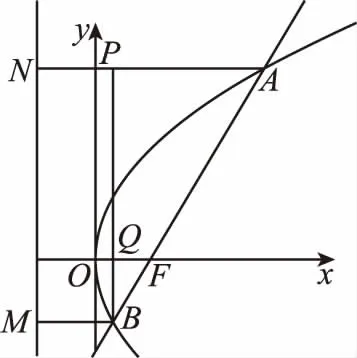
【例題7】(2016·四川卷理·8)設O為坐標原點，P是以F為焦點的拋物線y2=2px(p>0)上任意一點，M是線段PF上的點，且|PM|=2|MF|，則直線OM的斜率的最大值為

( )

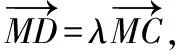
從上述例題的闡述中，可以得到以下幾點啟示：(1)在解析幾何的教學中，需要重視各種曲線的定義辨析，舍得花時間與學生一起認真審題，逐條“翻譯”題中的每一句話，讓學生清晰地知道解析幾何分析的大致程序；(2)關注解析幾何中“設而不求”和“幾何關系”兩種意識的培養，加強學生運算能力的引導，教師多示范性地演示計算詳情，培養學生良好的計算習慣；(3)關注刪除幾何證明選講后引起的蝴蝶效應，解析幾何實質也是幾何的一份子，利用幾何圖形分析數學問題是數形結合思想的完美呈現，有助于提升學生直觀想象素養.

(作者單位：廣東省汕尾市華南師范大學附屬中學汕尾學校)