“不等式解法及其應(yīng)用”復(fù)習(xí)策略探究

甘肅

董 強

(作者單位：甘肅省隴南市西和縣第一中學(xué))

“不等式解法及其應(yīng)用”復(fù)習(xí)策略探究

甘肅

董 強

不等式是刻畫現(xiàn)實世界中不等關(guān)系的重要數(shù)學(xué)模型，是進一步學(xué)習(xí)數(shù)學(xué)和解決其他數(shù)學(xué)問題的基礎(chǔ)和有利工具.現(xiàn)行各版本高中教材中，除選修4—5“不等式選講”外，只在必修5第三章“不等式”與選修1—2(文)、選修2—2(理)第二章“推理與證明”中涉及不等式相關(guān)內(nèi)容.縱觀近幾年高考試題對解不等式問題的考查，主要涉及指數(shù)不等式、對數(shù)不等式、絕對值不等式、分式不等式、一元二次不等式等，且多與函數(shù)、數(shù)列、圓錐曲線、概率、向量等綜合考查，解題時從函數(shù)性質(zhì)，如函數(shù)的單調(diào)性、奇偶性及3個二次關(guān)系等入手，便可找到問題的突破口，從而快速解題.

一、巧用不等式的性質(zhì)轉(zhuǎn)化求解

不等式的性質(zhì)是求解不等式的重要方法之一，將一些待求解的不等式通過不等式的性質(zhì)轉(zhuǎn)化為一元二次不等式、分式型不等式、絕對值不等式等常見類型進行求解往往是解不等式的重要途徑.

(一)一元二次不等式的解法

【例1】(2015·江蘇卷·7)不等式2x2-x<4的解集為________.

【答案】(-1，2).

評注：首先將指數(shù)式化為一元二次不等式x2-x-2<0，再求解.一元二次不等式、一元二次方程以及所對應(yīng)的二次函數(shù)關(guān)系密切，即一元二次方程的兩個根(Δ≥0)正好是所對應(yīng)二次函數(shù)圖象與x軸交點的橫坐標(biāo)，也恰是一元二次不等式解集的“分界點”.所以求解一元二次不等式一般要與一元二次方程和二次函數(shù)的圖象緊密關(guān)聯(lián)，首先對不等式進行變形，將不等號一端二次項系數(shù)化為大于0，另一端為0，即化為ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0)的形式，再計算相應(yīng)的判別式Δ，當(dāng)Δ≥0時，求出相應(yīng)的一元二次方程的根，最后根據(jù)對應(yīng)的二次函數(shù)的圖象，寫出一元二次不等式的解集，當(dāng)Δ<0時，結(jié)合二次函數(shù)圖象寫出所對應(yīng)一元二次不等式的解集．

(二)分式型不等式的解法

( )

【答案】A.

評注：分式型不等式求解時首先應(yīng)通過移項將右邊化為0，再根據(jù)符號法則“同號得正，異號得負(fù)”的原則進行分類討論，將分式型不等式化歸為整式型不等式(組)進行求解，注意轉(zhuǎn)化過程的等價變形，對小于等于及大于等于0型的分式不等式在變形為整式不等式后，應(yīng)去掉使得分母等于0的值．含有兩個因式的分式型不等式都可以化歸為一元二次不等式進行求解，對于含有多個因式的分式型不等式求解時還可以使用“穿針引線”的方法.

(三)絕對值不等式的解法

絕對值不等式是高考的重難點之一,求解此類題目的關(guān)鍵在于如何去掉絕對值符號,進而轉(zhuǎn)化為常見不等式,簡化運算.

【例3】(2016·全國卷Ⅰ理·24)已知函數(shù)f(x)=|x+1|-|2x-3|.

(Ⅰ)在圖中畫出y=f(x)的圖象；

(Ⅱ)求不等式|f(x)|>1的解集.

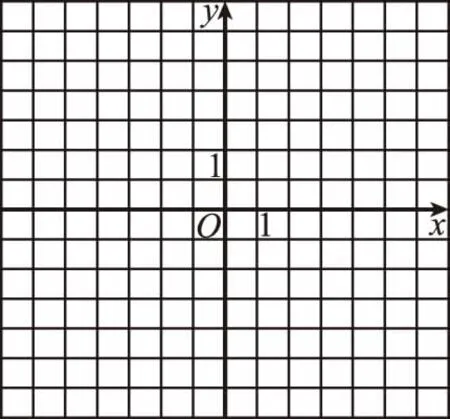
評注：對含有絕對值的不等式的求解一般采用零點分段討論法，單絕對值一般分兩類去絕對值，雙絕對值一般分三類去絕對值，求解形如|x-a|±|x-b|≥c的不等式時先求兩個絕對值的“零點”，再劃分區(qū)間，分類去絕對值符號，分別解去掉絕對值后的不等式，最后對三類結(jié)果求并集，即為原不等式的解集，應(yīng)特別注意區(qū)間的端點值.另外，對含有絕對值的不等式求解時，還可以利用絕對值的幾何意義，由于|x-a|+|x-b|與|x-a|-|x-b|分別表示數(shù)軸上與x對應(yīng)的點到與a，b對應(yīng)的點的距離之和與距離之差，因此對形如|x-a|±|x-b|c(c>0)的不等式，利用絕對值的幾何意義求解更直觀.如本題也可以先畫出y=|f(x)|的圖象以及直線x=1，然后根據(jù)圖象寫出解集.

二、利用函數(shù)的性質(zhì)求解不等式

(一)利用函數(shù)的單調(diào)性

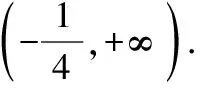
評注：可以采用分段函數(shù)分類討論的思想，結(jié)合函數(shù)的單調(diào)性求解不等式，單調(diào)性是函數(shù)的重要性質(zhì)之一，和不等式的關(guān)系極其緊密，充分利用函數(shù)的單調(diào)性解不等式是數(shù)學(xué)核心素養(yǎng)的重要體現(xiàn).

(二)利用函數(shù)奇偶性求解不等式

【例5】(2010·課程標(biāo)準(zhǔn)卷理·8)設(shè)偶函數(shù)f(x)滿足f(x)=x3-8(x≥0)，則{x|f(x-2)>0}=

( )

A.{x|x<-2或x>4} B.{x|x<0或x>4}

C.{x|x<0或x>6} D.{x|x<-2或x>2}

【答案】B.

評注：根據(jù)偶函數(shù)的性質(zhì)，結(jié)合函數(shù)的圖象，將不等式的求解轉(zhuǎn)化為函數(shù)零點的求解問題，通過數(shù)形結(jié)合，直觀地看出所要求解不等式的解集，這是利用函數(shù)的性質(zhì)求解不等式的巧妙之處.

三、不等式的基本應(yīng)用

(一)基本不等式在解決實際問題時的應(yīng)用

【例6】(2017·江蘇卷·10)某公司一年購買某種貨物600噸，每次購買x噸，運費為6萬元/次，一年的總存儲費用為4x萬元，要使一年的總運費與總存儲費用之和最小，則x的值是________.

【答案】30.

(二)不等式在線性規(guī)劃中的應(yīng)用

【例7】(2016·全國卷Ⅰ·文理16)某高科技企業(yè)生產(chǎn)產(chǎn)品A和產(chǎn)品B需要甲、乙兩種新型材料.生產(chǎn)一件產(chǎn)品A需要甲材料1.5 kg，乙材料1 kg，用5個工時；生產(chǎn)一件產(chǎn)品B需要甲材料0.5 kg，乙材料0.3 kg，用3個工時. 生產(chǎn)一件產(chǎn)品A的利潤為2 100元，生產(chǎn)一件產(chǎn)品B的利潤為900元.該企業(yè)現(xiàn)有甲材料150 kg，乙材料90 kg，則在不超過600個工時的條件下，生產(chǎn)產(chǎn)品A、產(chǎn)品B的利潤之和的最大值為________元.

【答案】216 000.

評注：利潤最大、效益最高、材料最省、花費最少等實際問題往往涉及線性規(guī)劃的知識，線性規(guī)劃是每年高考必考的內(nèi)容，多以選填題的形式出現(xiàn)，基本題型有給出約束條件求目標(biāo)函數(shù)的最值，通過目標(biāo)函數(shù)的最值確定相應(yīng)參數(shù)的值，通過實際問題背景蘊含線性規(guī)劃知識等.線性規(guī)劃一般有縱截距、斜率、兩點間的距離、點到直線的距離等命題視角,解決此類問題常利用數(shù)形結(jié)合的思想.本題先將實際問題轉(zhuǎn)化為線性規(guī)劃問題，再利用線性規(guī)劃的知識進行求解.

(三)三角形不等式的應(yīng)用

評注：絕對值三角不等式在求解雙絕對值不等式的最值問題時具有快速、簡潔的特征，尤其是向量形式的三角不等式更具明顯的幾何意義，即“三角形的兩邊之和大于第三邊，兩邊之差小于第三邊”.

四、有關(guān)不等式復(fù)習(xí)策略的教學(xué)建議

(一)立足課本，強化基礎(chǔ)

“立足課本”是“不等式”教與學(xué)的歸宿，重新解讀教材，激活已學(xué)知識，清晰課本中各概念的內(nèi)涵與外延，注重課本知識的內(nèi)在聯(lián)系，傳承教材結(jié)論，總結(jié)思想方法，將課本中的有關(guān)不等式的性質(zhì)的來龍去脈、各種變式熟練掌握，強化不等式學(xué)習(xí)的理論基礎(chǔ)，能夠根據(jù)不等式的相關(guān)性質(zhì)進行不等式的求解、探索與證明，這是不等式學(xué)習(xí)必須注意的一個方面.

(二)瞄準(zhǔn)高考，注重通法

高考試題中有關(guān)不等式的求解類題目都是一些比較重要的、常規(guī)的不等式，對這些不等式的求解必須要注重通性通法，如上述的一元二次不等式、分式型不等式、絕對值不等式等的求解，都有著一般的“套路”，這些通法的學(xué)習(xí)是不等式求解中非常關(guān)鍵的環(huán)節(jié). 通性、通法是解決不等式相關(guān)問題的根本方法，不偏、不難、不怪，而運用函數(shù)的性質(zhì)解不等式等是區(qū)分學(xué)生是否具有較好數(shù)學(xué)素養(yǎng)的重要指標(biāo).

(三)巧妙轉(zhuǎn)化，融會貫通

含參數(shù)問題，不等式恒成立問題，與數(shù)列、函數(shù)結(jié)合的不等式問題常常出現(xiàn)在高考的壓軸題中，是區(qū)分學(xué)生是否能得高分的重要部分，對這些試題中不等式的求解一定要審時度勢，審題時把題目中的疑點、難點、關(guān)鍵點找出來，當(dāng)解題遇到障礙時，利用其他知識將不等式的求解問題巧妙轉(zhuǎn)化，做到不同知識點的融會貫通，如構(gòu)造函數(shù)、分離參數(shù)等可以將不等式求解轉(zhuǎn)化為函數(shù)，利用函數(shù)的相關(guān)性質(zhì)、函數(shù)的圖象等巧妙解題.

(四)構(gòu)建模型，重視應(yīng)用

(作者單位：甘肅省隴南市西和縣第一中學(xué))