微分方程在動態目標檢測與跟蹤中的應用研究

梁哲銘

微分議程在許多領域都有重要應用，文章以導彈追擊動態目標為例，從最簡單的二維導彈追擊問題建立了常微分方程，可以得到導彈的軌跡方程，根據微分方程在Matlab中模擬可以得到導彈追擊圖，進而求得導彈擊中目標的。

當今社會，許多實際問題的處理，或者決策的產生，都越來越離不開高等數學知識的運用。微分是高等數學的重要內容，微分方程建立的模型在許多領域中占有著十分重要的地位。現代各學科各領域都與微分方程建模有著密切聯系，例如軍事、經濟金融、預測等方面。微分方程在軍事領域中可用于追蹤和檢測問題，把這些問題進行定量分析。

某軍一導彈基地發現正東方向1海里處海面上有一艘敵艦以速度向正北方向行駛。該基地立即發射導彈追擊敵艦，導彈速度是5，自動導航系統使導彈在任一時刻都能對準敵艦，求導彈運行的曲線方程，敵艦行駛多遠時，導彈將其擊中？

1模型建立

假設導彈基地在坐標原點建立直角坐標系，如圖1所示，敵艦在x軸上的A處。假設導彈在t時刻的位置是M（x，y），敵艦的位置是N，如圖1所示。

導彈的軌跡曲線為OP，因為導彈始終對準敵艦，直線MN是M點處的切線，即伺

2模型求解

假設t時刻敵艦和導彈的坐標是一樣為（x（t），Y（t））

（1）假設導彈的速度為w=5v，可得方程

（2）因為自動導航系統使導彈在任一時刻都能對準敵艦，所以導彈的速度平行于敵艦與導彈頭位置的差向量，可得導彈運動軌跡的參數方程為：

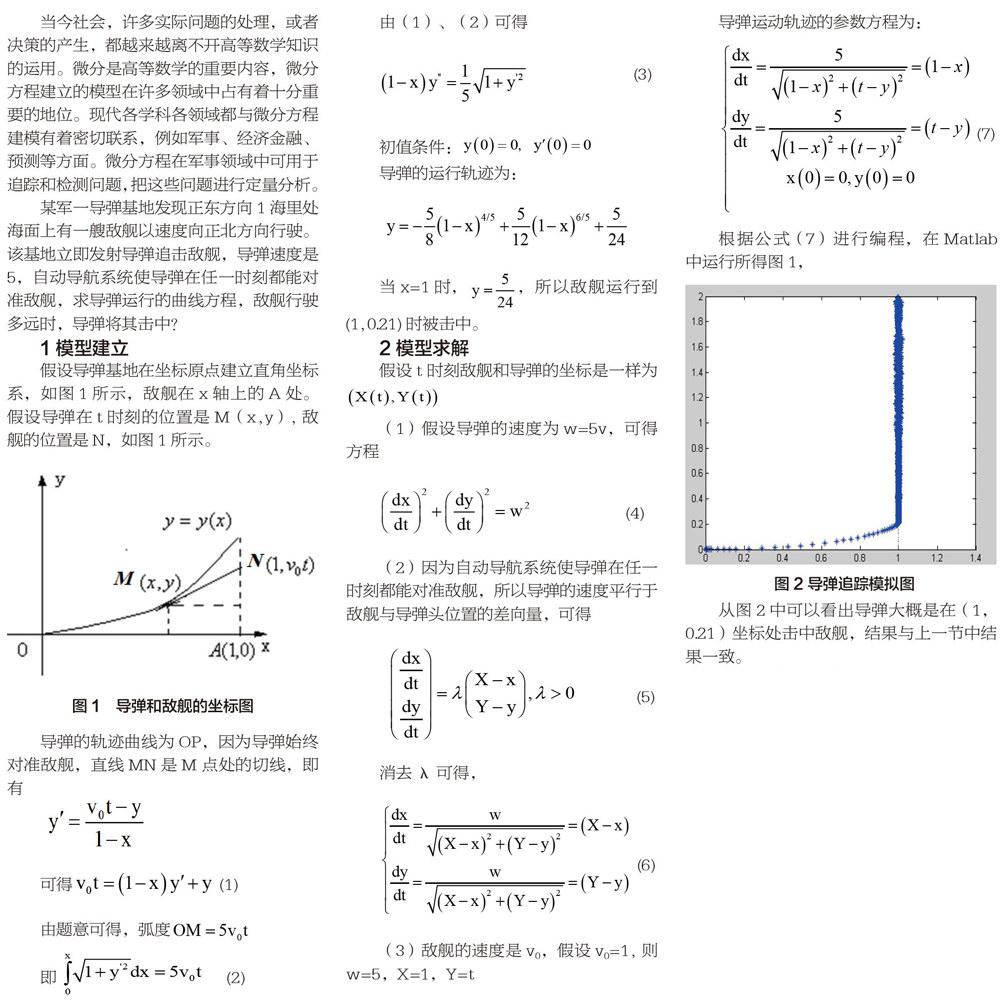
根據公式（7）進行編程，在Matlab中運行所得圖1，

從圖2中可以看出導彈大概是在（1，0.21）坐標處擊中敵艦，結果與上一節中結果一致。

3模型評價與不足

模型利用了均勻物體的質心就為該物體的形心這一的原理來建立模型并轉化為二維平面問題，使問題簡單明了，利用幾何中，曲線的相切性質列出常微分方程，再求解方程。但是在實際的軍事中，問題要復雜很多，并且是動態變化的，敵機不可能和地面一直保持相同的距離，敵機和導彈的長度的忽略會影響會使計算結果有偏差，并且需要考慮風力、重力等影響因素，敵機在發現被跟蹤時肯定會加速，所以它的速度不可能是恒定不變的，這些問題在后期的研究中都是需要考慮的因素。