基于組合預測算法的光柵信號新細分方法研究*

陳自然,李 鋼,趙 建,田 偉(重慶理工大學機械檢測技術與裝備教育部工程研究中心,時柵傳感及先進檢測技術重慶市重點實驗室,重慶 400054)

機床工業是國民經濟的基礎產業,其發展水平是衡量國家工業化程度的重要標志。大力發展數控機床產業是國家工業化道路上的必經之路。數控機床作為現代先進制造的主流加工設備,已成為國際制造業和國防工業競爭的焦點。數控機床的不斷發展對機床關鍵功能部件提出了更高的要求。目前市場上主要采用光柵傳感器作為機床位置檢測與反饋部件,其測量精度直接關系系統主機性能[1-3]。

光柵測量的本質是對莫爾條紋的計數實現位移測量。柵距精度決定測量的精度,柵距的密度決定測量分辨力,要實現高精度高分辨力測量,就必須要求光柵柵距刻劃得又精又密。精密位移測量領域中往往要求在大量程范圍內實現高精度、高分辨力測量以解決宏觀結構下微細尺度的精密檢測與控制。如果通過減小柵距來提高測量分辨力,不僅加工難度大,在工藝上也不易實現。并且光學衍射極限制約了光柵制造工藝向刻劃密集方向的發展[4-5]。目前提高位移傳感器測量分辨力的主流技術就是引入信號輔助細分手段[6-8]。

根據細分原理的不同,可以將光柵信號的細分方法分為機械細分法、光學細分法、電子學細分法和微處理器細分法。其中光學細分法和機械細分法工藝復雜,成本較高,精度較低,因此應用范圍受到限制。而電子細分和微處理器細分所得到的細分信號能直接輸入到控制系統實現位置反饋,且原理簡單,因此得到廣泛的應用。按照對光柵輸出信號細分參數的不同,可以將電子學細分法分為幅值型細分法[9-10]、相位型細分法[11]和鎖相倍頻細分法[12]等。微處理器細分法主要是以處理器為硬件,采用智能算法實現光柵信號細分[13-16]。受光柵光源準直性、光柵刻劃誤差、機械安裝誤差等因素影響,光柵輸出信號不是標準的正弦和正交信號,其中包含直流電平,兩路信號幅值不等,相位不正交及噪聲干擾等因素,這些將嚴重影響光柵細分精度。以上傳統光柵信號細分方法對傳感器輸出的原始信號波形質量要求較高。為了減少原始信號波形失真對光柵細分精度的影響,國內外學者在提高原始信號質量方面做了大量的誤差修正方面的研究[17-20]。這些工作復雜、難度大,效果也比較有限。

本文將光柵運動的空間位置和運動時間相關聯,充分利用光柵自身制造精度,研究一種光柵信號自適應細分方法及細分誤差修正算法,此細分方法與光柵輸出信號正弦性無關。

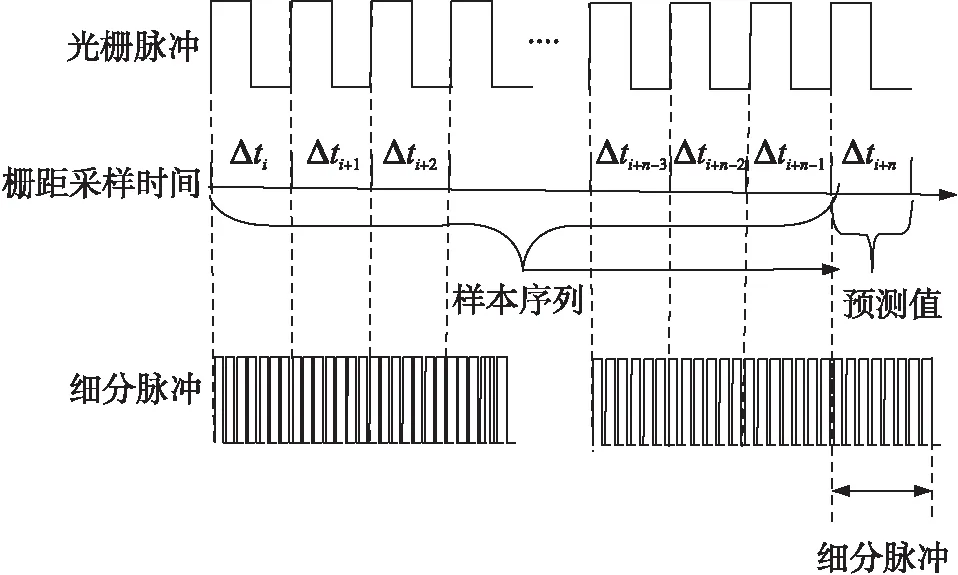
圖1 光柵細分原理

1 光柵信號細分原理

光柵在運動過程中,空間位置與運動時間互為映射,利用空間和時間的對應關系,提出一種利用時間基準測量空間的新方法。光柵運動單位柵距觸發輸出空間脈沖信號,通過采樣空間脈沖時間建立運動時間與運動空間之間的映射關系。如圖1所示,通過觸發生成的柵距采樣時間Δti,Δti+1,…Δti+n-1作為序列樣本,建立數學模型,預測光柵觸發當前柵距的采樣時間Δti+n。根據細分倍數,在采樣時間Δti+n內由微處理器采用脈寬調制技術(PWM)發出帶空間當量的細分脈沖,從而實現光柵信號細分。

2 光柵細分算法研究

由于光柵運動的隨機性,在不同的運動狀態中,光柵柵距采樣時間和空間映射關系也在動態變化,為了減小由于運動狀態改變帶來的信號細分誤差,針對不同運動狀態特性,研究采用指數平滑法和灰色算法相結合的組合式預測算法建模,提高光柵信號細分精度。

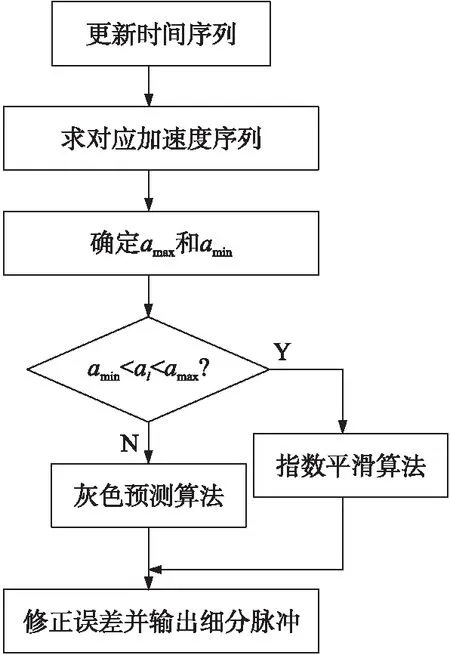
圖2 狀態判斷流程圖

2.1 光柵運動狀態判斷

單位柵距的位移是固定的Δs,處理器系統在單位柵距內采用ARM芯片中定時器的捕獲(Capture)單元測量光柵輸出信號的脈沖寬度,即實際單位柵距觸發的采樣時間,能夠采樣得到時間序列Δti,Δti+1,…Δti+n-1,由于機械系統具有慣性和二階動態特性,在單位微位移(柵距)范圍內可近似認為光柵運動滿足連續和平穩性要求,采用式(1)、式(2)可求出兩個相鄰單位柵距內的光柵運動加速度ai。

(1)

(2)

式中:vi和vi+1分別為第i和i+1個柵距的通過速度。利用式(1)、式(2)可以根據時間序列Δti,Δti+1,…Δti+n-1求出相對應加速度序列(并取絕對值)|ai|,|ai+1|,…|ai+n-2| 并求出加速度序列中的最大值amax與最小值amin。光柵運動狀態判斷流程圖如圖2所示。

當加速度的絕對值大于加速度序列中最大值amax或小于最小值amin,對應于變速狀態,否則認為光柵運動在平穩狀態。

2.2 指數平滑法

指數平滑法常應用于中短期的發展趨勢預測。光柵作平穩運動時,由于慣性的作用,光柵運動速度在單位柵距微位移中不會發生驟變,通過每一個柵距觸發的采樣時間相對穩定,因而采樣時間序列的態勢具有穩定性和規律性。當前柵距的采樣時間量與采樣時間樣本序列具有較強相關性。因此當光柵在平穩運動狀態時,可采用二次指數平滑法進行建模。

首先建立一次指數平滑模型如式(3)所示:

(3)

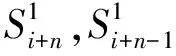
在一次指數平滑的基礎上在一次做平滑處理即得到二次指數平滑模型:

(4)

(5)

式中:

(6)

(7)

2.3 灰色算法

當光柵由平穩運動過渡到不平穩運動狀態時,在這個階段數據規律變化較劇烈,研究采用灰色預測算法,利用其在小樣本數據中具有較強魯棒性的特點,建立光柵柵距觸發采樣時間和運動空間的映射關系。

(8)

式中:時間序列Δt(0)為原始序列,進行一階累加得到一階累加序列(9):

(9)

構建灰色預測模型對應的微分方程為式(10):

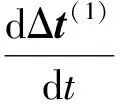
(10)

式中:β為發展灰數,μ為內生控制灰數。簡化模型為:

Y=Bα

(11)

(12)

利用最小二乘估計法得到;

(13)

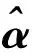
(14)

最后累減得到最后的預測值:

(15)

令k=i+n-1,則預測第i+n個柵距的通過時間為:

(16)

2.4 細分誤差修正模型

為了消除信號細分誤差累積,保證細分精度,研究預測的柵距觸發采樣時間與真實采樣時間值所構成的誤差序列樣本之間的相關性,采用馬爾科夫修正模型預測當前柵距的采樣時間誤差,從而修正上述預測算法所帶來的時間誤差對空間細分誤差的影響。

Pt+1=P0[P(1)]t+1

(17)

式(17)是馬爾科夫鏈預測模型,其中P0為初始時刻無條件的概率分布。Pt+1為t+1時刻的概率分布,P(1)為一步轉移概率矩陣:

(18)

式中:pij為從i狀態轉移到j狀態的概率。

根據時間預測算法得到的預測結果,計算出預測值與真實值之間的誤差,根據指數平滑法與灰色預測算法的特性將誤差劃分為不同的區間,并構建馬爾科夫預測模型,最后對誤差進行修正。當確定了當前誤差所處的狀態區域后,即可得到最后的修正值,最終得到修正后的第i+n個柵距的預測通過時間為Δt:

(19)

式中:δ為當前柵距觸發采樣時間誤差修正值。

3 細分實驗研究

為減少機械運動導致的機械振動和環境溫度變化給實驗帶來的影響,研究采用大理石平臺搭建所需的實驗系統,其中包含兩個用于比對實驗的HEIDENHAIN公司的36 000線精度為±1″圓光柵ROD880。兩個圓光柵采用高彈性聯軸節與數控轉臺同軸安裝。以可編程多軸控制器PMAC作為控制核心,采用Kollmorgen直驅電機作為運動部件驅動轉臺帶動兩個光柵同步運動。光柵1采用海德漢IBV660B細分盒進行400倍細分,細分后每個脈沖所代表的空間當量為0.09″,光柵2采用組合預測算法的細分方法,由于光柵柵距固定為36″,本實驗細分倍數為100,每個細分后脈沖所代表的空間當量為0.36″,細分脈沖采用脈寬調制(PWM)技術發送出去,其脈沖頻率和光柵運動速度成正比。將光柵通過海德漢IBV660B細分盒進行400倍細分的脈沖和采用組合預測算法細分的脈沖同步采集計數得到細分誤差。

圖3 光柵細分實驗系統

圖4 光柵細分實驗結構方框圖

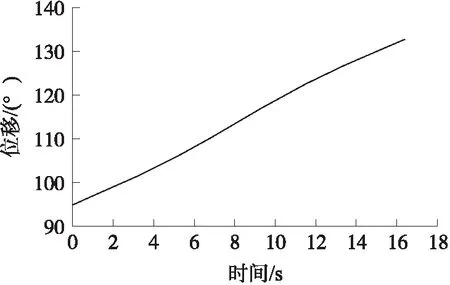
圖5 光柵運動時間-位移圖

為驗證本算法的可行性,圖5為光柵在數控轉臺驅動下角位移運動曲線圖,光柵從95.6°運動到132.8°歷時16.406 1 s,圖6是采用ARM芯片中定時器的捕獲(Capture)單元測量光柵輸出信號的脈沖寬度,即實際單位柵距觸發的采樣時間,運動過程分別是平穩運動和非平穩運動兩個狀態,具體包含低速近似勻速運動(2.0 °/s),勻加速運動,高速近似勻速運動(2.8 °/s),勻減速運動,低速近似勻速運動(2.0 °/s)。

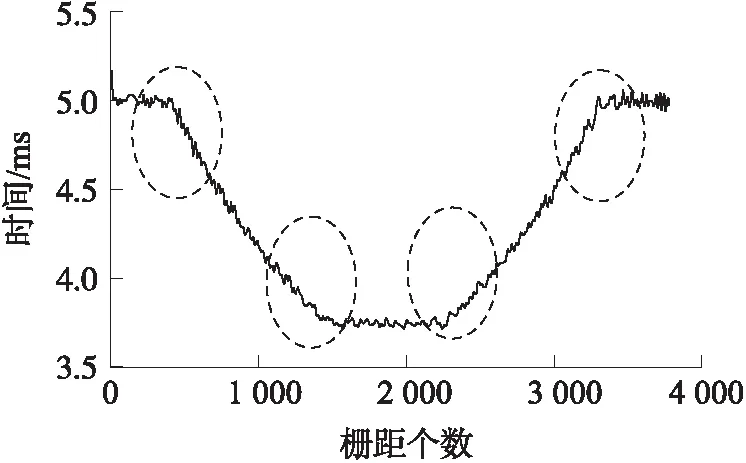
圖6 單位柵距運動采樣時間

本系統采用的是組合式的預測算法,當光柵作平穩運動(近似勻速、勻加速或減速)時,采用指數平滑法對經過當前柵距的采樣時間進行預測,當光柵在運動狀態發生改變時(近似勻速與變速運動來回切換的“臨界”狀態,如圖6中圓圈部分所示),采用的是灰色預測算法。

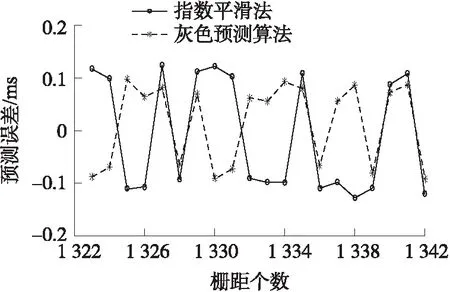
圖8 加速到高速近似勻速的預測采樣時間誤差對比圖

為了突出組合預測算法的有效性,做了3組對比實驗進行分析。第1組為不平穩狀態下的指數平滑法和灰色算法實驗數據精度比較,即圖6中圓圈部分所示的近似勻速與變速運動切換的“臨界”狀態條件下柵距觸發采樣時間的預測精度對比分析,具體數據如圖7～圖10所示。

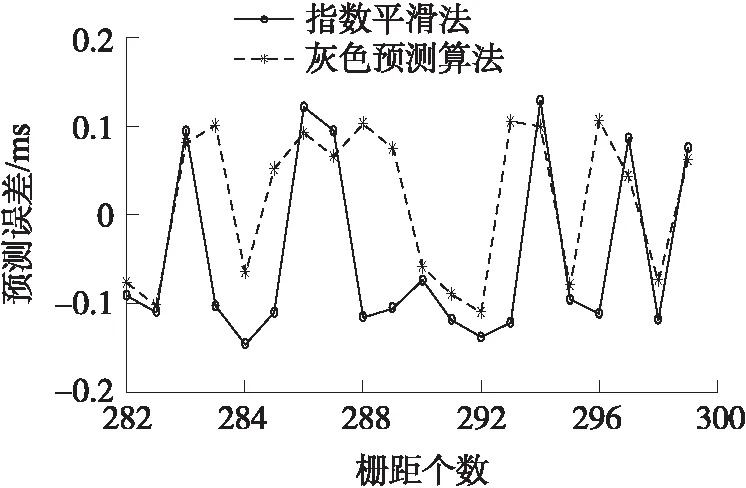
圖7 低速近似勻速到加速的預測采樣時間誤差對比圖

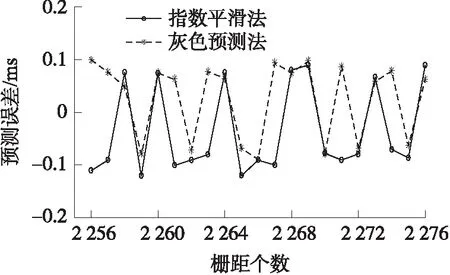
圖9 高速近似勻速到勻減速的預測采樣時間誤差對比圖

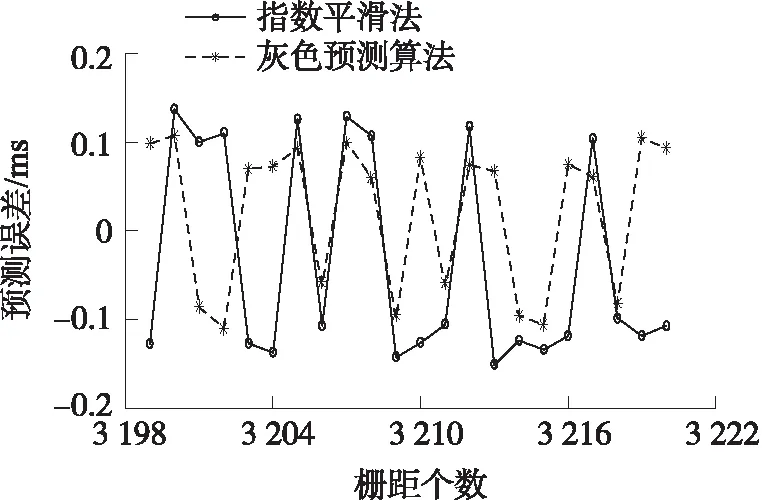
圖10 勻減速到低速近似勻速的預測采樣時間誤差對比圖

由圖7～圖10可知,在“臨界”狀態,灰色預測算法能夠將光柵柵距觸發采樣的時間誤差控制在±0.11 ms,對應的細分誤差為±0.75″,而采用指數平滑法只能將光柵柵距采樣時間誤差控制在±0.15 ms,對應的細分誤差為±1.01″。并且相較于指數平滑法,灰色預測算法在“臨界”區,預測誤差更加平穩。因此當光柵運動處于“臨界”狀態時采用灰色預測算法能夠減少預測誤差。

圖11 指數平滑法與組合式預測算法細分誤差對比圖

第2組實驗是采用指數平滑法、灰色算法與兩者相結合的組合預測算法對整個運動過程的光柵柵距采樣時間值進行預測分析,對比各細分誤差效果,實驗數據如圖11和圖12所示。灰色預測算法對應的采樣時間誤差±0.13 ms,對應的細分誤差為±0.92″,而采用指數平滑法對應的采樣時間誤差±0.17 ms,對應的細分誤差為±1.06″。相對于在光柵整個的運動過程中使用單一的預測算法,組合式的預測算法誤差較小為±0.12 ms,對應的細分誤差為±0.79″。

圖12 灰色算法與組合式預測算法細分誤差對比圖

第3組是采樣時間誤差修正前后的光柵信號細分誤差對比實驗。圖13是馬爾科夫修正前后的預測誤差對比圖,沒修正前采樣時間誤差為±0.12 ms,對應的細分誤差為±0.79″,修正后采樣時間誤差為0.081 ms,對應的細分誤差為±0.56″,馬爾科夫修正模型能夠對運動過程中的預測采樣時間誤差進行修正。

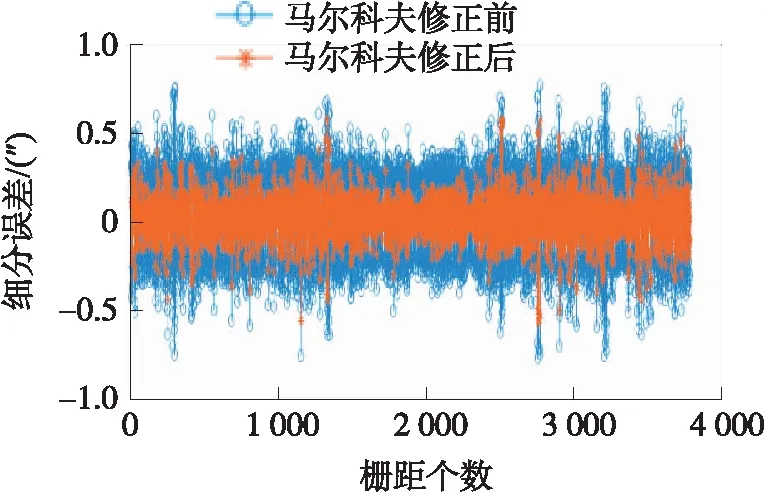
圖13 修正前后細分誤差對比圖

4 結論

①在分析不同運動狀態特性的基礎上,研究采用簡單迭代算法,充分利用指數平滑法的線性特征和灰色算法的魯棒性,綜合平衡算法的實時性和預測精度,提出一種光柵信號自適應細分新方法,實現光柵信號細分,盡量減小由于加速度波動給信號細分精度帶來的影響。

②為消除誤差累計,提高光柵信號細分精度,研究采用馬爾科夫修正模型處理預測值與真實值的誤差組成的誤差序列,通過分析樣本之間的相關性,預測當前柵距的采樣時間誤差,通過修正采樣時間值實現提高光柵信號細分精度的目的。

③本文充分利用運動時間和運動空間的映射關系,提出一種利用時間基準測量空間的新方法。此方法突破了傳統的光柵細分方法對光柵輸出信號波形質量高要求的局限,最大限度利用光柵自身制造精度,將傳統光柵信號對細分電路的硬件高要求用軟件算法來靈活處理,成本低,精度高,并可適用于磁柵、感應同步器等傳感器中,在精密測量領域具有重要通用性。