停機工況下風(fēng)電機組的載荷對比分析

文 | 王煜翔，田德，閆肖蒙，林俊杰，羅濤

（作者單位：華北電力大學(xué)可再生能源學(xué)院）

風(fēng)電機組運行在復(fù)雜的自然環(huán)境中，所受載荷情況非常復(fù)雜，載荷計算是風(fēng)電機組認證和設(shè)計中的首要問題，是結(jié)構(gòu)強度校核與部件選型的基礎(chǔ)。風(fēng)電機組廠家在機組設(shè)計過程中，如果設(shè)計載荷偏低，當(dāng)遇到極端風(fēng)況時，風(fēng)電機組輕則出現(xiàn)故障，重則發(fā)生機組倒塌事故，造成嚴(yán)重的經(jīng)濟損失；如果設(shè)計載荷偏高，對材料的性能要求過高，從而大幅度增加風(fēng)電機組的總體造價。因此，載荷計算在風(fēng)電機組設(shè)計中占著重要的地位。

目前，風(fēng)電機組載荷計算大部分采用國際通用標(biāo)準(zhǔn)——國際電工委員會2005年修訂的IEC 61400-1標(biāo)準(zhǔn)（以下簡稱IEC2005）。IEC2005標(biāo)準(zhǔn)有8種設(shè)計工況，包括：發(fā)電、發(fā)電兼故障、起動、正常關(guān)機、緊急關(guān)機、停機、停機兼故障以及運輸組裝維護與修理。其中，停機工況分為靜止和空轉(zhuǎn)兩種狀態(tài)，但是停機工況下的載荷設(shè)計是以靜止?fàn)顟B(tài)的載荷計算結(jié)果為依據(jù)，還是以空轉(zhuǎn)狀態(tài)下的載荷計算結(jié)果為依據(jù)，目前尚無定論。基于此，本文以1.5MW水平軸風(fēng)電機組為模型，對停機工況下的靜止和空轉(zhuǎn)狀態(tài)的載荷計算結(jié)果進行對比分析，得出停機工況下的載荷設(shè)計依據(jù)。

風(fēng)電機組模型參數(shù)

載荷計算采用1.5MW雙饋異步風(fēng)電機組模型，詳細參數(shù)如表1所示；機組安全等級 A。風(fēng)電機組安全等級基本參數(shù)如表2所示。

停機風(fēng)況介紹

根據(jù)IEC2005，停機工況分為兩種風(fēng)況，極端風(fēng)速模型（EWM）和正常湍流模型（NTM）。

一、極端風(fēng)速模型（EWM）

極端風(fēng)速模型應(yīng)是穩(wěn)態(tài)風(fēng)速模型或湍流風(fēng)速模型，該風(fēng)速模型是基于參考風(fēng)速Vref與恒定的湍流標(biāo)準(zhǔn)偏差σ1。

對于穩(wěn)態(tài)風(fēng)速模型，50年一遇和1年一遇的極大風(fēng)速Ve50和Ve1作為高度z的函數(shù)，應(yīng)采用公式（1）、公式（2）進行計算：

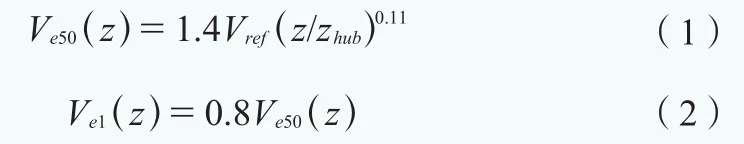
在穩(wěn)態(tài)極端風(fēng)速模型中，允許短時間內(nèi)與平均風(fēng)向有一定的偏離，應(yīng)假定恒定的偏航誤差在±15°范圍內(nèi)。

對于湍流極端風(fēng)速模型，50年和1年一遇的10min平均風(fēng)速是高度z的函數(shù)，應(yīng)采用公式（3）、公式（4）進行計算。

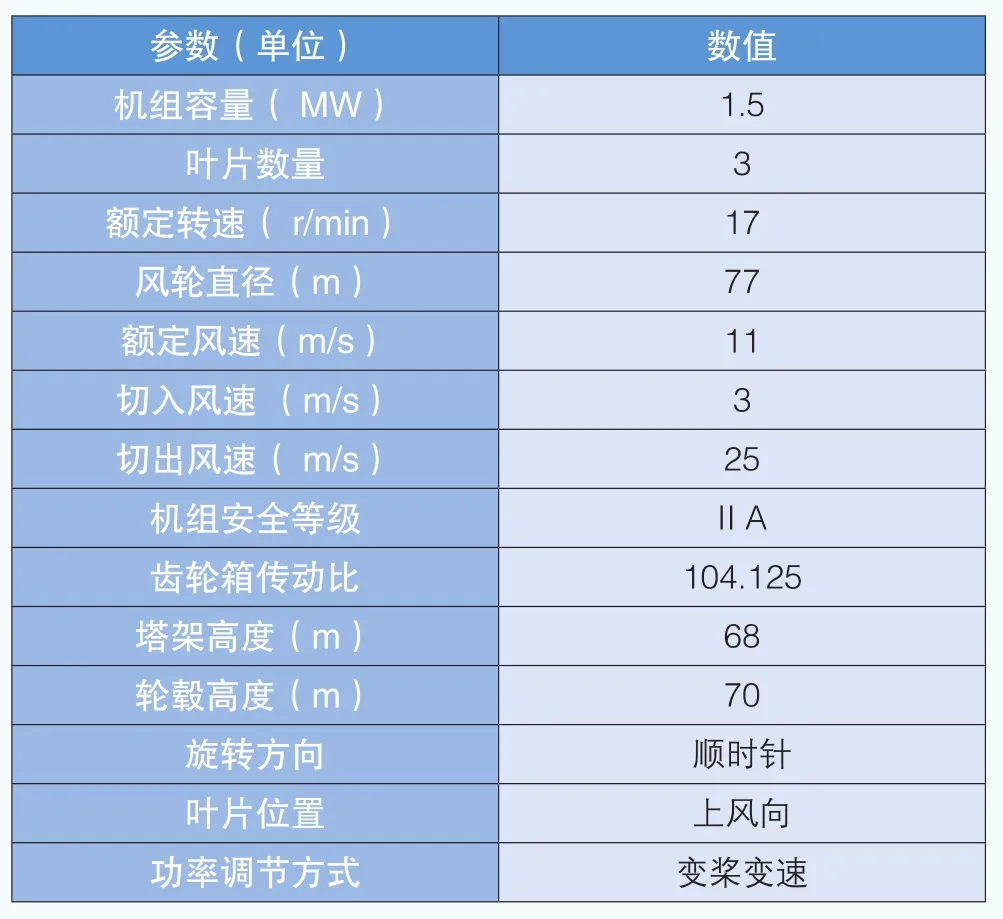
表1 風(fēng)電機組模型參數(shù)

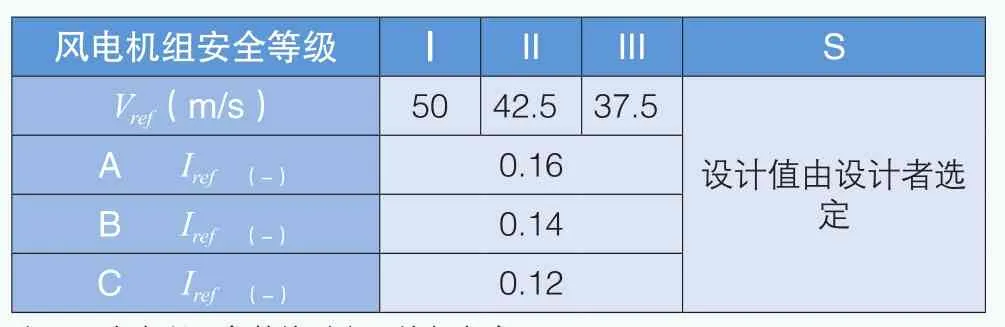
表2 風(fēng)電機組安全等級基本參數(shù)

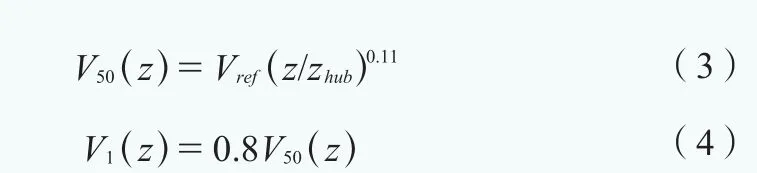
縱向湍流標(biāo)準(zhǔn)偏差為：

二、正常湍流模型（NTM）

對于正常湍流模型，輪轂高度處風(fēng)速的湍流標(biāo)準(zhǔn)偏差的代表值σ1應(yīng)由該風(fēng)速下湍流標(biāo)準(zhǔn)偏差分布的90%分位數(shù)確定。對于標(biāo)準(zhǔn)風(fēng)電機組等級，σ1采用公式（6）進行計算：

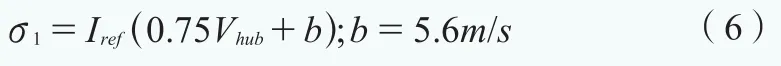
計算模型

在停機工況下，運用Kaimal和Mann湍流譜密度模型，分別對靜止和空轉(zhuǎn)兩種狀態(tài)的風(fēng)電機組進行載荷計算，對計算結(jié)果進行分析對比，得出結(jié)論。

Bladed湍流風(fēng)模型采用三種模型進行仿真，分別是Von Karman、Kaimal以及Mann模型。目前風(fēng)電機組設(shè)計要求IEC標(biāo)準(zhǔn)規(guī)定采用Kaimal譜和Mann均勻切變湍流模型，停止使用Von Karman湍流模型。同時研究文獻中表明，應(yīng)用Kaimal和Mann模型計算出的極限載荷和等效疲勞載荷相對于Von Karman更為保守。基于此，本文采用Kaimal和Mann湍流風(fēng)模型進行仿真計算。

一、Mann均勻切變湍流模型

Mann湍流譜密度模型定義了一個三維速度譜張量，與Von Karman模型稍微不同，假設(shè)該模型產(chǎn)生的隨機速度場以輪轂高度風(fēng)速流過風(fēng)電機組，某一點的速度分量譜可對譜張量進行積分計算，那么無量綱的單面譜公式為：

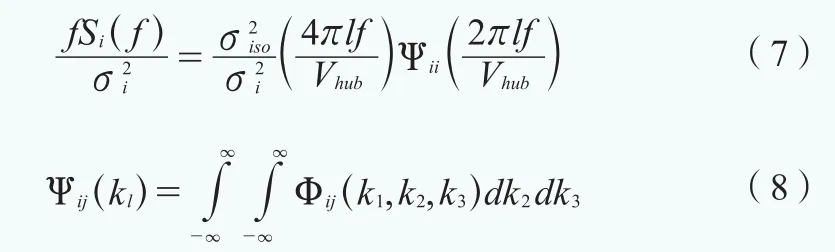
式中，f代表頻率，Hz；Si代表單邊速度分量譜；下標(biāo)i代表速度分量方向，1為縱向，2為橫向，3為豎向；、l分別代表無切變、各向同性方差和尺度參數(shù)；當(dāng)i＝j(luò)時，Ψij是一維的波數(shù)自譜密度；當(dāng)i≠j且分量方差為公式（9）時，Ψij為正交譜；Vhub表示輪轂高度處的風(fēng)速，下標(biāo)hub表示輪轂高度處的位置。

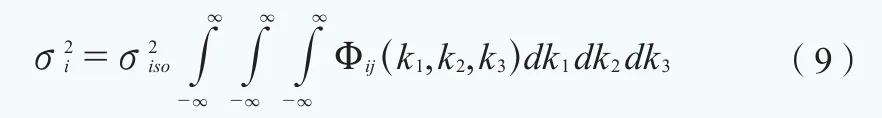
同樣，對于垂直于縱向的多個空間分離點，相關(guān)函數(shù)為：

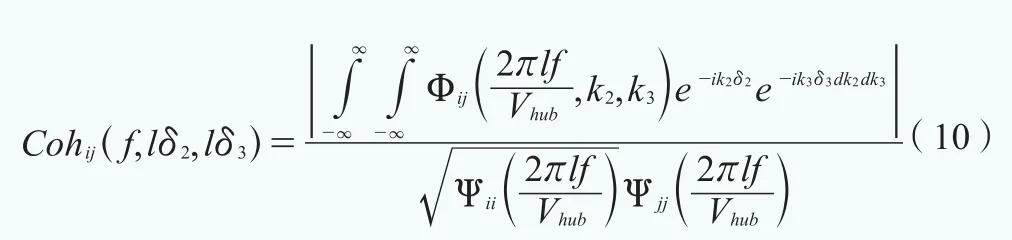
式中，Φij（k1，k2，k3）是三維無量綱速度譜張量；k1，k2，k3是3個分量方向的無量綱空間波數(shù)；δ2，δ3為無量綱空間分離的矢量分量。

二、Kaimal譜和指數(shù)相干模型

Kaimal譜和指數(shù)相干模型同樣定義了一個三維速度譜張量，模型中湍流分量方差率以及豎向速度分量的方程形式與Mann均勻切變湍流模型略有不同，Kaimal分量功率譜密度無量綱形式為：

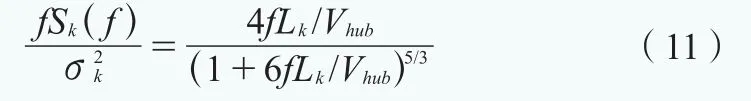
式中，f代表頻率，Hz；Sk代表單邊速度分量譜；下標(biāo)k代表速度分量方向，1為縱向，2為橫向，3為豎向；Lk代表速度分量積分尺度參數(shù)；σk代表速度分量標(biāo)準(zhǔn)偏差，其表達式為：

式中，σ1和Λ1分別是湍流標(biāo)準(zhǔn)偏差和尺度參數(shù)。無量綱互譜相干模型為：

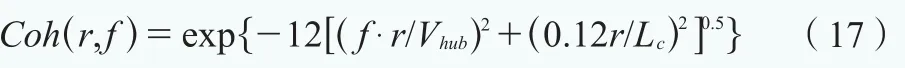
式中，r代表兩點之間分離矢量在垂直于平均風(fēng)向平面上的投影值；f代表頻率，Hz；Lc代表相干尺度參數(shù)，取8.1Λ1（Λ1為尺度參數(shù)）。

Kaimal與Mann模型的相關(guān)參數(shù)如表3、表4所示。

停機工況下的設(shè)計載荷狀態(tài)如表5所示，在DLC6.1、DLC6.2和DLC6.3設(shè)計狀態(tài)下，采用極端風(fēng)速模型；在DLC6.4設(shè)計狀態(tài)下，采用正常湍流模型。

計算結(jié)果與分析

在進行停機工況的載荷設(shè)計時，若設(shè)計載荷偏小，在風(fēng)電機組的實際運行中可能發(fā)生超載現(xiàn)象。在風(fēng)電機組實際運行過程中，對風(fēng)電機組進行載荷設(shè)計時，應(yīng)采取較大的載荷計算結(jié)果，這樣才能保證機組在實際條件下更加安全可靠的運行，預(yù)防飛輪、倒塔等事故的發(fā)生。

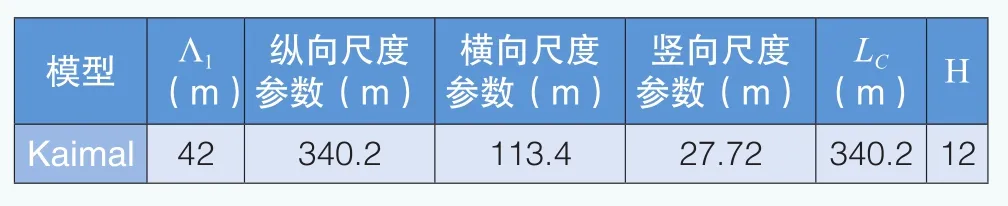
表3 Kaimal模型相關(guān)參數(shù)

表4 Mann模型相關(guān)參數(shù)

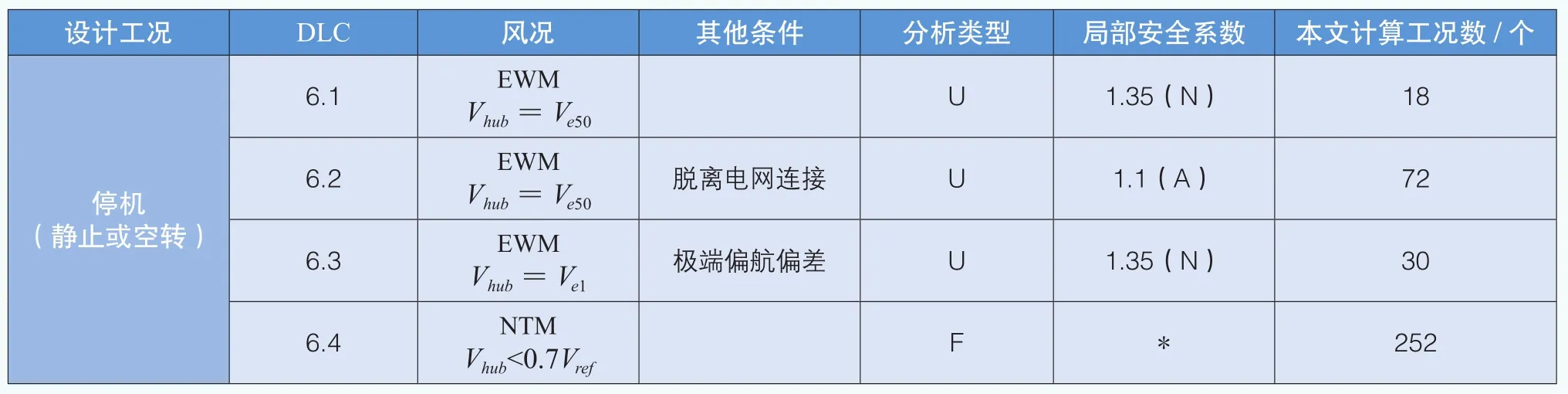
表5 停機工況設(shè)計載荷狀態(tài)

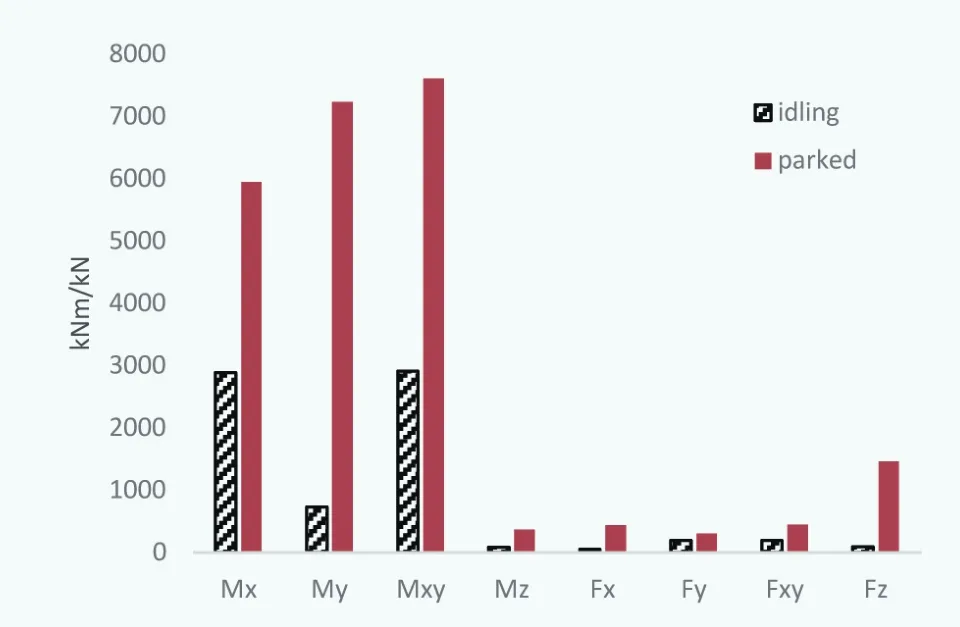
圖1 葉片根部極限載荷分量對比 （Kaimal模型）

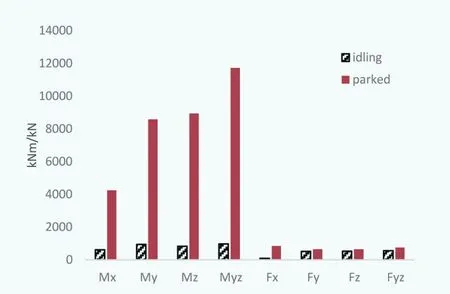
圖2 旋轉(zhuǎn)輪轂極限載荷分量對比（Kaimal模型）

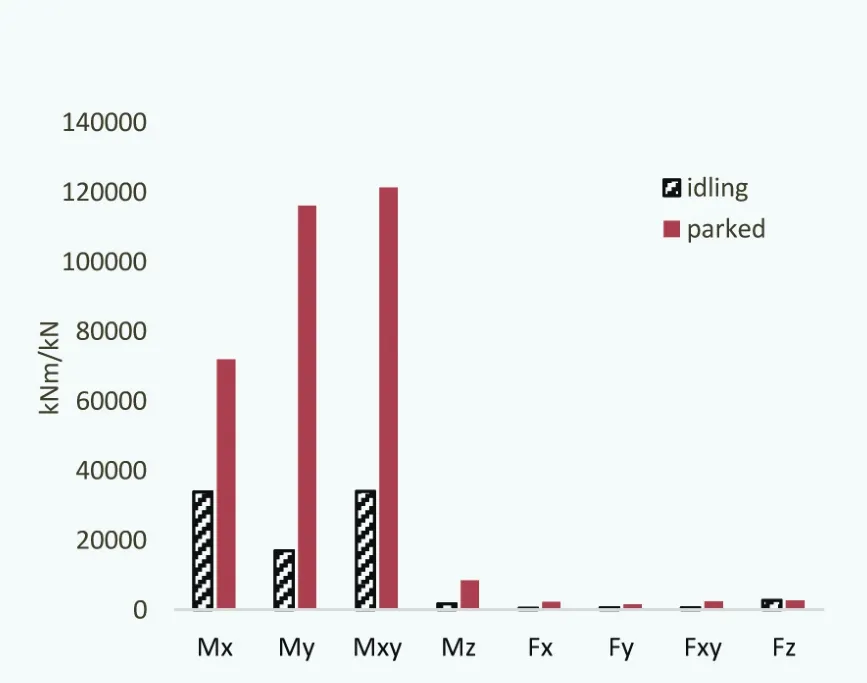
圖3 塔架底部極限載荷分量對比（Kaimal模型）

一、極限載荷對比分析

在Kaimal與Mann風(fēng)湍流模型下，通過對風(fēng)電機組關(guān)鍵位置處的的極限載荷計算，比較兩種模型下風(fēng)電機組關(guān)鍵位置處極限載荷的要求情況并加以分析。

（一）Kaimal模型停機工況極限載荷計算結(jié)果

在停機工況下，采用Kaimal模型對風(fēng)電機組葉片、輪轂、塔架等關(guān)鍵部位進行極限載荷計算，得出靜止和空轉(zhuǎn)狀態(tài)下的極限載荷分量計算結(jié)果，如圖1－圖3所示。在葉片根部、輪轂和塔架底部位置，靜止?fàn)顟B(tài)下的極限載荷分量明顯大于空轉(zhuǎn)狀態(tài)。

通過圖1可以看出，在葉片根部，靜止和空轉(zhuǎn)狀態(tài)極限載荷分量相差最小的為Fy，相差率（兩種狀態(tài)下同一極限載荷分量的差值與較小值之比）為60%；兩者極限載荷分量相差最大的為Fz，差值高于一個數(shù)量級。這是由于在空轉(zhuǎn)狀態(tài)下，極端風(fēng)況的風(fēng)載荷，一部分由葉片自身承受，一部分轉(zhuǎn)化為風(fēng)輪旋轉(zhuǎn)的動能；在靜止?fàn)顟B(tài)下，風(fēng)載荷全部由葉片自身承受，極限載荷分量較大。

通過圖2可以看出，在輪轂位置處，靜止?fàn)顟B(tài)下的極限載荷分量Mz、Myz比空轉(zhuǎn)狀態(tài)下大一個數(shù)量級。產(chǎn)生這種現(xiàn)象的原因與葉根相似，由于在空轉(zhuǎn)狀態(tài)下，極端風(fēng)況的風(fēng)載荷，一部分由輪轂自身承受，一部分轉(zhuǎn)化為旋轉(zhuǎn)的動能；在靜止?fàn)顟B(tài)下，風(fēng)載荷全部由輪轂部分承受，極限載荷分量較大。

通過圖3可以看出，在塔架底部的極限載荷分量中，兩種狀態(tài)下的Fz相差較小，其他極限載荷分量靜止?fàn)顟B(tài)均比空轉(zhuǎn)狀態(tài)大且差別明顯，兩種狀態(tài)下的My相差最大，該分量下靜止?fàn)顟B(tài)為空轉(zhuǎn)狀態(tài)的8倍。極限載荷分量Fz是由于在塔架坐標(biāo)系中，z方向為垂直方向，塔架底部在z方向承受的力Fz是風(fēng)電機組機艙以及塔架的重力，該力幾乎不受風(fēng)載荷的影響，因此極限載荷分量Fz相差很小。而在其他載荷分量處相差較大，是由于塔架底部承受的是機艙、葉片及塔架本身的力。在靜止?fàn)顟B(tài)下，葉片、輪轂等重要部件受力大于空轉(zhuǎn)狀態(tài)，因此，塔架底部在靜止?fàn)顟B(tài)下受力同樣大于空轉(zhuǎn)狀態(tài)。

綜上所述，在Kaimal模型停機工況下，在空轉(zhuǎn)狀態(tài)下計算得出的極限載荷分量相對較小，在靜止?fàn)顟B(tài)下計算得出的極限載荷分量較大。因此，在采用Kaimal模型時，停機工況下應(yīng)根據(jù)靜止?fàn)顟B(tài)的極限載荷計算結(jié)果，進行機組極限載荷設(shè)計。

（二）Mann模型停機工況極限載荷計算結(jié)果

在停機工況下，采用Mann模型對風(fēng)電機組葉片、輪轂、塔架等關(guān)鍵部位進行極限載荷計算，得出靜止和空轉(zhuǎn)狀態(tài)下的極限載荷分量計算結(jié)果，如圖4－圖6所示。在停機工況下，在葉片根部、輪轂和塔架底部位置，靜止?fàn)顟B(tài)下的極限載荷分量同樣大于空轉(zhuǎn)狀態(tài)下的極限載荷分量。與Kaimal模型相比，Mann模型下空轉(zhuǎn)與靜止?fàn)顟B(tài)時的極限載荷分量差距較小，其極限載荷分量差值小于一個數(shù)量級，這是由于Kaimal模型與Mann模型設(shè)置的參數(shù)不同。

通過圖4可以看出，在葉根位置，靜止與空轉(zhuǎn)狀態(tài)下的極限載荷分量Fy差距較小。這是由于在葉片坐標(biāo)系中，y方向垂直于風(fēng)速方向，受風(fēng)載荷的影響較小，因此兩種狀態(tài)下的極限載荷分量Fy差別不大。這種情況在Kaimal模型中的葉根極限載荷分量Fy中也有體現(xiàn)，產(chǎn)生這種情況的原因與Mann模型相同。

通過圖5、圖6可以看出，在輪轂和塔架底部位置處，Mann模型在靜止和空轉(zhuǎn)狀態(tài)下的極限載荷分量分布與Kaimal模型相似。

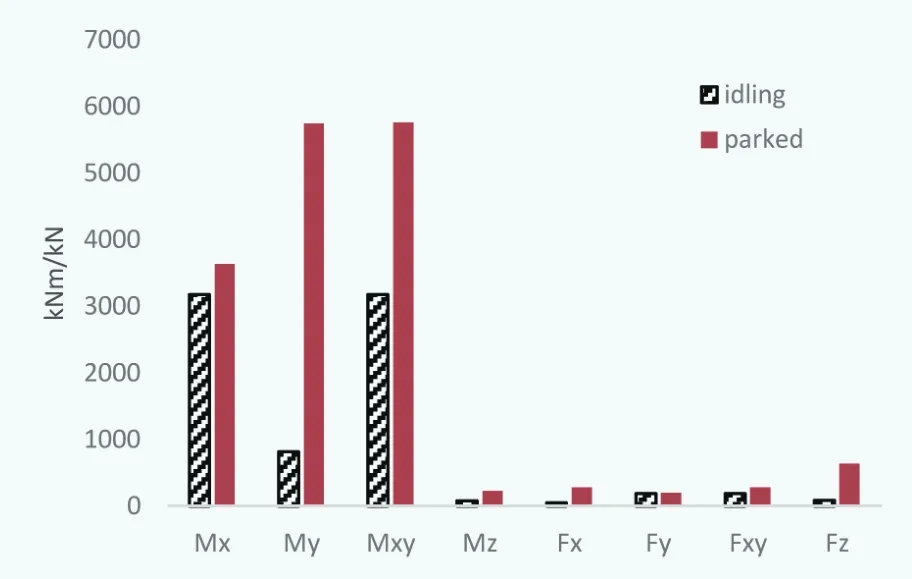
圖4 葉片根部極限載荷分量對比（Mann模型）

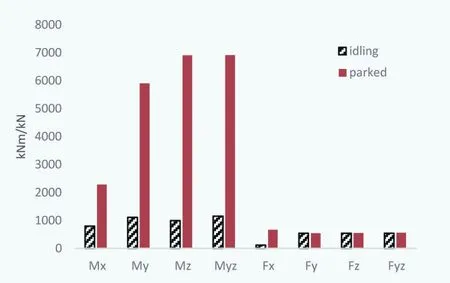
圖5 旋轉(zhuǎn)輪轂極限載荷分量對比（Mann模型）

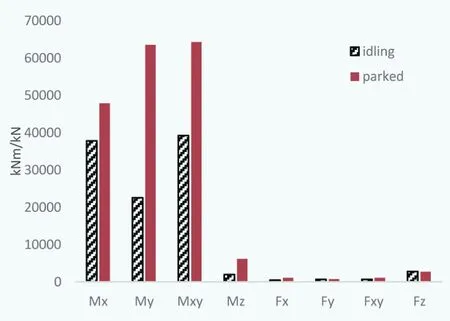
圖6 塔架底部極限載荷分量對比（Mann模型）

綜上所述，在Mann模型停機工況下，按照IEC2005標(biāo)準(zhǔn)得出的極限載荷計算對比結(jié)果與Kaimal模型相同，即在空轉(zhuǎn)狀態(tài)下的極限載荷分量較小，在靜止?fàn)顟B(tài)下的極限載

荷分量較大。因此，得出與Kaimal模型一致的結(jié)論，停機工況下應(yīng)根據(jù)靜止?fàn)顟B(tài)的極限載荷計算結(jié)果，進行機組極限載荷設(shè)計。

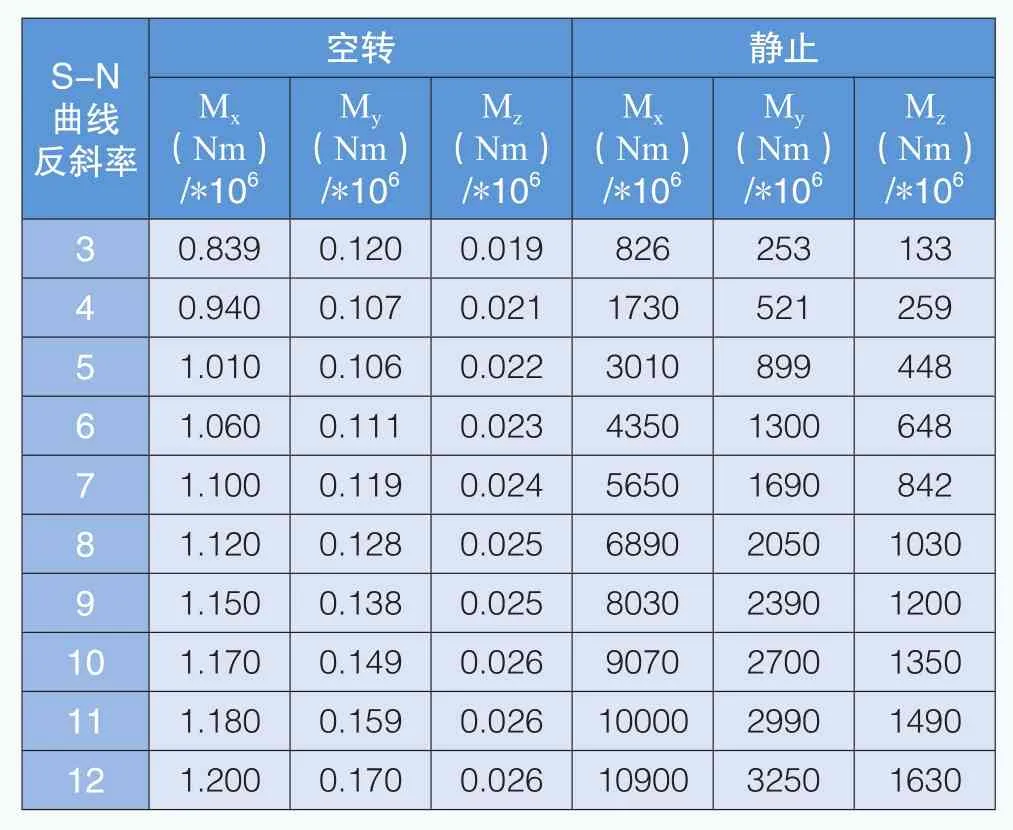
表6 葉片根部載荷分量對比（Kaimal模型）

表7 旋轉(zhuǎn)輪轂載荷分量對比（Kaimal模型）

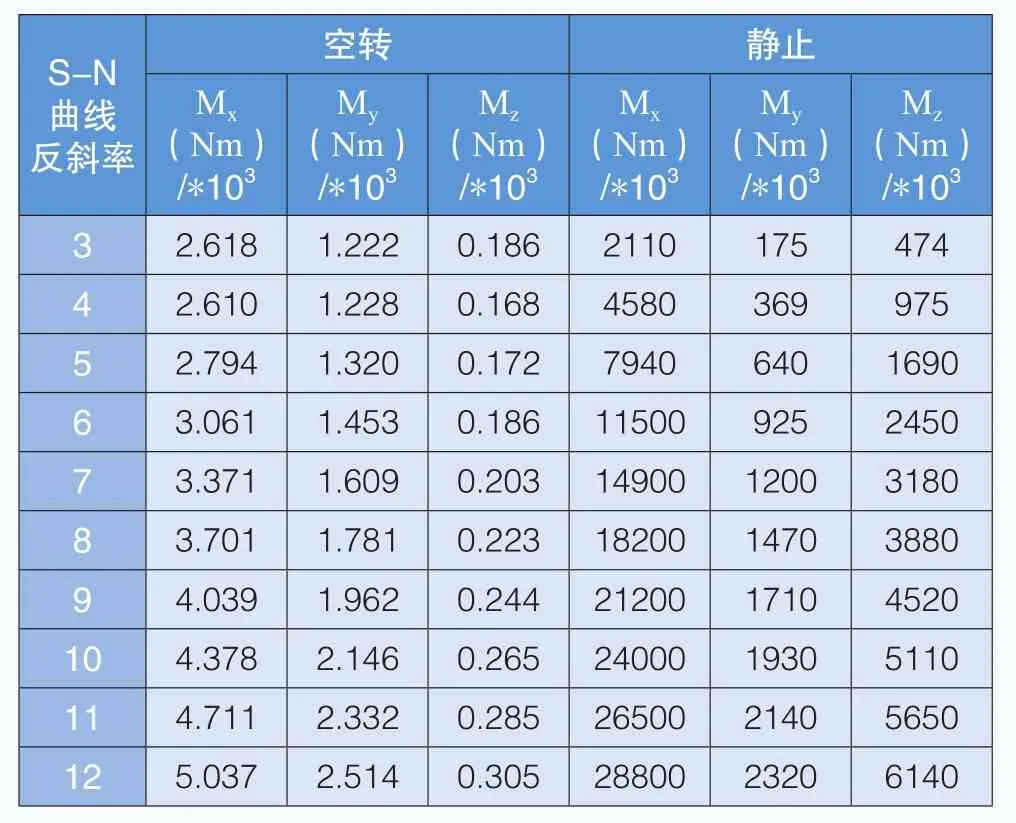
表8 塔架底部載荷分量對比（Kaimal模型）

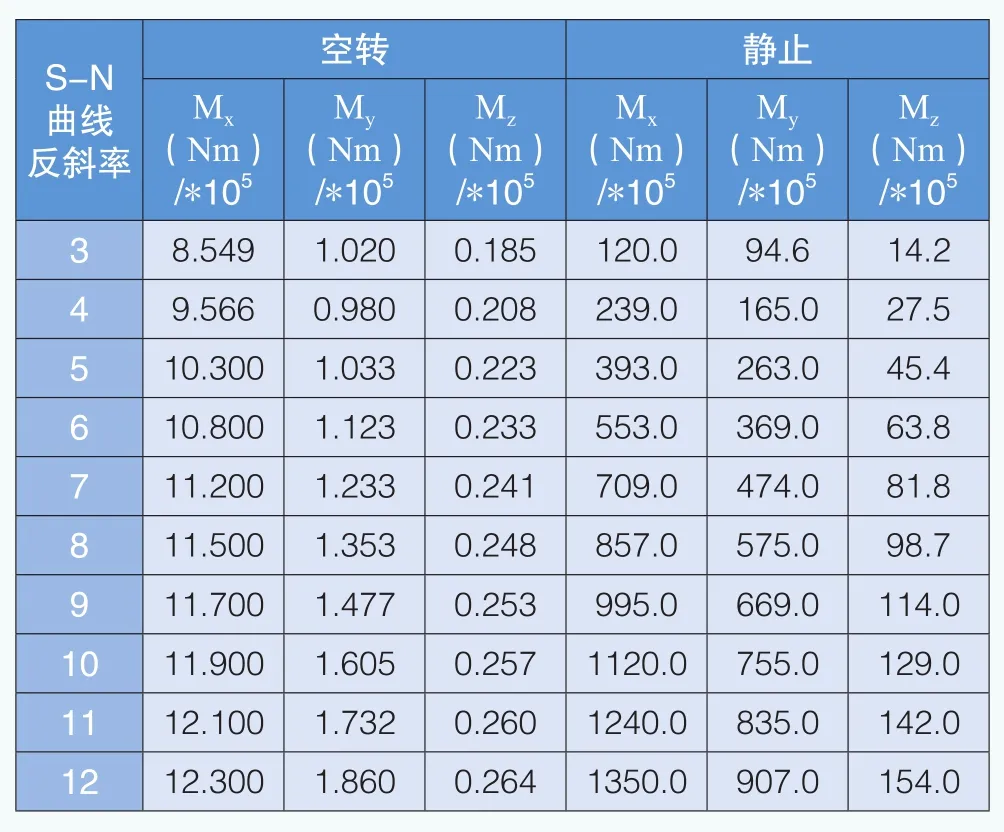
表9 葉片根部載荷分量對比（Mann模型）

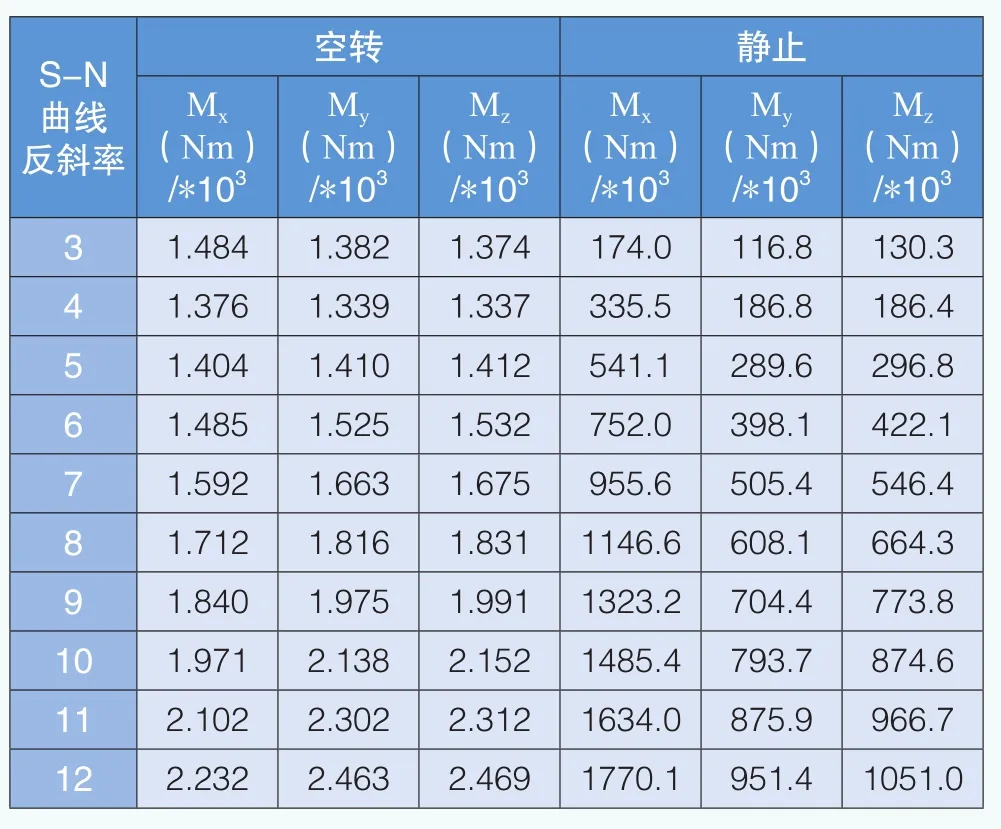
表10 旋轉(zhuǎn)輪轂載荷分量對比（Mann模型）

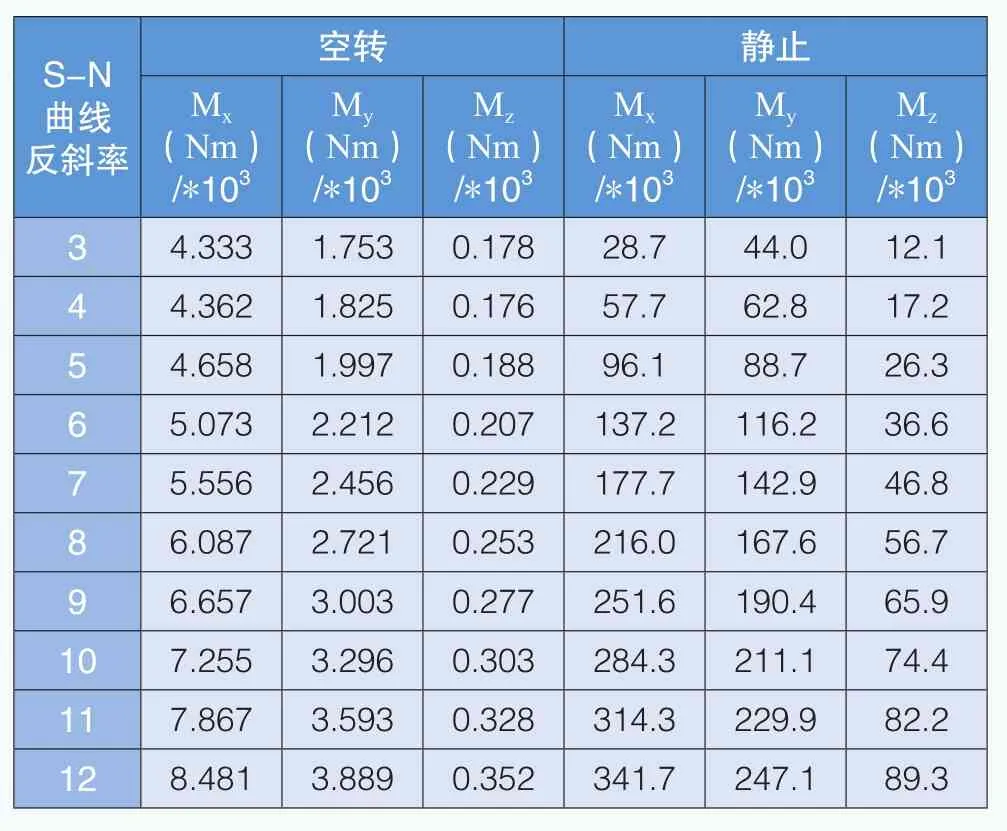
表11 塔架底部載荷分量對比（Mann模型）

（三）停機工況極限載荷設(shè)計選取

根據(jù)Kaimal模型和Mann模型極限載荷計算結(jié)果的對比分析，得出結(jié)論：在停機工況下，在葉片根部、輪轂和塔架底部位置，采用靜止?fàn)顟B(tài)計算得出的極限載荷分量較大，采用空轉(zhuǎn)狀態(tài)計算得出的極限載荷分量較小。因此，考慮到實際環(huán)境中的運行情況，應(yīng)以靜止?fàn)顟B(tài)下的極限載荷計算結(jié)果為依據(jù)進行極限載荷設(shè)計。

二、疲勞載荷對比分析

在Kaimal與Mann風(fēng)湍流模型下，通過對風(fēng)電機組關(guān)鍵位置處的等效疲勞載荷計算，比較兩種模型下風(fēng)電機組關(guān)鍵位置處等效疲勞載荷的要求情況并加以分析。

S-N曲線為疲勞壽命曲線，疲勞壽命是疲勞失效時所經(jīng)受的應(yīng)力或應(yīng)變的循環(huán)次數(shù)。不同的S-N曲線反斜率，如表中所示（數(shù)字3到12）分別代表風(fēng)電機組不同部件所用的材料。

（一）Kaimal模型停機工況疲勞載荷計算結(jié)果

在停機工況下，采用Kaimal模型、應(yīng)用雨流計數(shù)統(tǒng)計對風(fēng)電機組葉片、輪轂、塔架等關(guān)鍵部位進行疲勞載荷計算，得出靜止和空轉(zhuǎn)狀態(tài)下的等效疲勞載荷，如表6－表8所示。在葉片根部、輪轂和塔架底部位置，靜止和空轉(zhuǎn)狀態(tài)下的彎矩等效疲勞載荷差距較大。

在Kaimal模型下，二者最小的差距出現(xiàn)在表7， 即旋轉(zhuǎn)輪轂與固定輪轂的S-N曲線反斜率為3的位置，Mx相差454倍；最大的差距出現(xiàn)在表6， 即葉片根部的S-N曲線反斜率為12的位置，Mz相差62692倍。

綜上所述，在Kaimal模型停機工況下，采用靜止?fàn)顟B(tài)計算出的等效疲勞載荷遠遠大于空轉(zhuǎn)狀態(tài)。因此，停機工況下根據(jù)靜止?fàn)顟B(tài)的等效疲勞載荷計算結(jié)果，機組安全性更高。

（二）Mann模型停機工況疲勞載荷計算結(jié)果

在停機工況下，采用Mann模型、應(yīng)用雨流計數(shù)統(tǒng)計對風(fēng)電機組葉片、輪轂、塔架等關(guān)鍵部位進行疲勞載荷計算，得出靜止和空轉(zhuǎn)狀態(tài)下的等效疲勞載荷，如表9－表11所示。在葉片根部、輪轂和塔架底部位置，靜止和空轉(zhuǎn)狀態(tài)下的彎矩等效疲勞載荷差距也較大，但與Kaimal模型相比，差距相對較小。

在Mann模型下，二者最小的差距出現(xiàn)在表11，即塔架底部載荷S-N曲線反斜率為3的位置，Mx相差7倍；二者最大的差距出現(xiàn)在表10，即旋轉(zhuǎn)輪轂載荷S-N曲線反斜率為12的位置，Mx相差793倍。

綜上所述，在Mann模型停機工況下，靜止?fàn)顟B(tài)所計算出的等效疲勞載荷遠遠大于空轉(zhuǎn)狀態(tài)。因此，為保證風(fēng)電機組的載荷設(shè)計更加安全可靠，停機工況下應(yīng)根據(jù)靜止?fàn)顟B(tài)的等效疲勞載荷計算結(jié)果。

（三）停機工況疲勞載荷設(shè)計選取

根據(jù)Kaimal模型和Mann模型等效疲勞載荷計算結(jié)果的對比分析，得出結(jié)論：在停機工況下，在葉片根部、輪轂和塔架底部位置，采用靜止?fàn)顟B(tài)計算得出的等效疲勞載荷遠遠大于空轉(zhuǎn)狀態(tài)計算得出的等效疲勞載荷。因此，考慮到實際環(huán)境中的運行情況，應(yīng)以靜止?fàn)顟B(tài)下的等效疲勞載荷計算結(jié)果為依據(jù)進行疲勞載荷設(shè)計。

結(jié)論

基于IEC2005標(biāo)準(zhǔn)，以1.5MW雙饋異步風(fēng)電機組為研究對象，在停機工況下分別采用Kaimal和Mann湍流譜密度模型，對靜止?fàn)顟B(tài)和空轉(zhuǎn)狀態(tài)下的風(fēng)電機組進行載荷計算。根據(jù)Kaimal和Mann模型下兩種狀態(tài)的極限載荷和等效疲勞載荷計算結(jié)果，依據(jù)風(fēng)電機組設(shè)計載荷選取原則，判斷應(yīng)以哪一種狀態(tài)的載荷結(jié)果作為停機工況下的載荷設(shè)計依據(jù)，增強機組在極端風(fēng)況下的抗破壞能力，提高機組的設(shè)計可靠性。得出結(jié)論如下：

（1）在停機工況Kaimal模型和Mann模型下，在風(fēng)電機組葉片、輪轂、塔架等關(guān)鍵位置，采用靜止?fàn)顟B(tài)計算得出的極限載荷分量均比空轉(zhuǎn)狀態(tài)大，最大相差一個數(shù)量級，所以應(yīng)以靜止?fàn)顟B(tài)下的極限載荷計算結(jié)果為依據(jù)進行極限載荷設(shè)計。

（2）在停機工況Kaimal模型和Mann模型下，在風(fēng)電機組葉片、輪轂、塔架等關(guān)鍵位置，采用靜止?fàn)顟B(tài)計算得出的等效疲勞載荷遠遠大于空轉(zhuǎn)狀態(tài)，最大的差距為62692倍，所以應(yīng)以靜止?fàn)顟B(tài)下的等效疲勞載荷計算結(jié)果為依據(jù)進行疲勞載荷設(shè)計。

（3）在停機工況Kaimal模型和Mann模型下，在風(fēng)電機組關(guān)鍵位置，采用靜止?fàn)顟B(tài)計算得出的極限載荷和等效疲勞載荷均大于空轉(zhuǎn)狀態(tài)。綜合考慮極限載荷和等效疲勞載荷，在進行停機工況的載荷設(shè)計時，應(yīng)以靜止?fàn)顟B(tài)的載荷計算結(jié)果為依據(jù)。