復雜網絡聚類及其在神經網絡中的應用

文/高超

計算機網絡技術的出現，推動了人類社會文明的快速發展，大數據時代以指數增長的速度創造著越來越多的數據。在以數據庫為核心的信息技術背景下，聚類分析在數據挖掘中的使用，能夠有效加快對信息的定位，并且，結合神經網絡的發展需要，聚類分析法的應用范圍更加廣闊。

1　復雜網絡研究概述

所謂復雜網絡，是指具有一定組織性、吸引子、小世界、無標度中部分或全部性質的網絡，并在結構與形式方面存在較高的自相似性。這一概念早在上個世紀90年代就已經得到廣泛認同，計算機網絡技術的發展，驗證了復雜網絡中的節點度分布服從冪律分布的特點，并在此基礎上建立了無標度網絡模型。自此，關于復雜網絡結構的研究進入到新的技術領域。

關于復雜網絡的研究，我國雖然起步較晚，但是，憑借眾多研究人員的努力，我國復雜網絡研究的進展速度驚人，在相關領域的滲透速度令世界各國矚目。經過長期的研究發現，復雜網絡普遍具有的社團結構特征，以及與之相對應的社團結構算法，為復雜網絡聚類分析法的提出奠定了基礎。

2　人工神經網絡的研究現狀

互聯網技術的出現，重新定義了人類所了解的世界，與現實世界相似，互聯網創造了一個虛擬的世界，并且，在這一虛擬世界中，也要嚴格遵守相關“生存規則”。隨著互聯網技術在生物技術、人工智能等領域的不斷滲透，關于人工神經網絡的研究逐漸浮出水面。

早期人工神經網絡的發展受技術條件的限制，多停留在理論研究階段，直至1957年，ERosenblat所提出的感知器模型，為人工神經網絡技術的工程化應用創造了可能。在此之后，關于人工神經網絡的研究進入到了“黃金時期”，各種具有創新性的理論研究成果，為人工神經網絡的實踐應用提供了理論支撐，實驗室中的相關研究結果，同樣證明了這一技術的可行性。

3　幾種常見的復雜網絡聚類分析方法

在神經網絡技術實現過程中，所使用到的復雜網絡聚類分析法主要包括K-Lin算法、傳統譜平分法、分裂算法。

3.1　K-Lin算法

基于對貪婪算法的研究，B.W.kernighan和S.Lin提出了一個新的聚類算法“K-Lin算法”，該算法將已知網絡進行社團劃分，利用增益函數表達兩個大小已知社團內部變數與連接兩個社團變數的差值Q。通過對比Q值，其中Q值最大的劃分網絡就是最佳的社團結構，在不斷的試探過程中，得到最佳算法。

然而，K-Lin算法也存在的一定的缺陷，這就是必須事先知道兩個社團的大小，否則，計算結果將存在不確定性。正因為此，K-Lin算法不能夠應用于位置網絡大小的實際網絡之中。

3.2　傳統譜平分法

在計算機圖形分割的實現過程中，基于Laplace矩陣特征值的譜平分法得到了較為廣泛的應用，這是由于傳統譜平分法能夠嚴格執行數學理論的各項要求。基于Laplace矩陣特征值的譜平分法根據無向量圖G對應的對稱矩陣L的不同特征值與特征向量進行網絡區分，其復雜程度較高，其中主要運算內容是對特征矩陣向量的求解。

由于傳統譜平分法在使用過程中需要將網絡進行一定比例的劃分，因此，對復雜網絡的首次二分結果，將直接影響到今后網絡劃分的正確性，所以，采用傳統譜平分法存在一定的算法冗余情況，其效果也并不理想。

3.3　分裂算法

在實際使用過程中，分列算法則依據網絡節點對的相似程度對節點對的邊進行刪除，在這一行為的不斷重復過程中，整個復雜網絡也就被劃分成了多個社團。研究人員可以根據社團劃分的情況，隨時終止算法進程，以避免復雜網絡過度分割后的情況出現。如圖1所示，在水平虛線逐漸下移的過程中，復雜網絡中的社團個數不斷增加，當水平虛線移至最底端時，也就達到了這一復雜網絡的最小社團劃分單位。

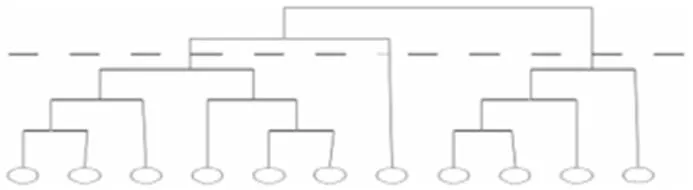
圖1：基于樹狀圖記錄算法的復雜網絡社團分割結果

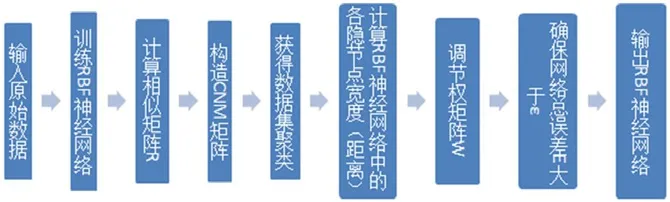
圖2：CNM聚類優化下的RBF神經網絡算法思想流程示意圖

4　基于CNM聚類優化的RBF神經網絡算法

由于RBF網絡中隱含基層函數的中心選取會對整體網絡的收斂特性造成一定的影響，同時也會降低網絡精度，這導致了RBF神經網絡所具有的優勢得不到有效發揮。然而，研究人員發現，在使用了CNM聚類算法的情況下，RBF神經網絡原本存在的問題得到了明顯改善，網絡質量、穩定性、精度均得到了不同程度的提高。

基于CNM聚類優化下的RBF神經網絡算法思想如圖2所示。

5　總結

在計算機網絡信息技術快速發展的今天，大數據技術的應用范圍不斷擴大，為實現對數據的有效管理和使用，則需要采用科學的復雜網絡聚類分析方法，對神經網絡進行優化，使其在實際應用中的范圍更加廣闊。