不確定非線性系統的事件驅動魯棒跟蹤控制

崔黎黎, 王曉薇, 吳　鵬, 王　利

(沈陽師范大學 科信軟件學院, 沈陽　110034)

在實際工業領域中,大多數被控對象具有高度非線性,很難獲得其精確的數學模型,這使得實際動態系統和系統的數學模型間普遍存在不確定性,從而導致系統的性能變差甚至不穩定,因此,控制器設計時魯棒性是研究者們所考慮的重點。非線性魯棒跟蹤控制研究如何設計控制器使系統在不確定性作用下能夠跟蹤一個給定的目標軌跡,一直是控制領域研究的一個重點內容。研究者們基于經典的控制理論,如變結構控制[1]、模型預測控制[2]、反演控制[3]、神經網絡控制[4]等,提出了各種魯棒跟蹤控制方法。然而,上述方法雖然實現了魯棒跟蹤,但大多數未考慮系統性能的優化。

近年來,自適應動態規劃方法(adaptive dynamic programming, ADP)由于具有自學習與優化能力,能夠有效解決動態規劃的“維數災”問題,現已成為了控制領域研究的熱點。 目前ADP理論在非線性系統的最優控制[5]、微分對策[6]、多智能體系統的最優控制[7]等方面已取得了許多重要的研究成果。在最優跟蹤控制方面,文獻[8]針對一類不確定連續非線性系統提出了基于評價網絡-控制網絡結構的神經網絡自適應魯棒器設計方法。文獻[9]基于ADP方法研究了一類不確定離散非線性系統的魯棒跟蹤控制問題。文獻[10]提出了一個在線策略增強學習算法,實現了一類未知非線性系統的H∞跟蹤控制。文獻[11]針對一類未知不確定性系統的跟蹤控制問題提出了一個數據驅動ADP算法。然而,上述控制器設計方法均未考慮網絡帶寬的限制,所設計的控制器是基于時間驅動的,采用實時更新的方式,因此網絡負荷和計算量較大,在實際應用中具有一定的局限性。據作者所知,目前基于ADP的不確定非線性系統的事件驅動魯棒跟蹤控制相關結果尚未見報道。

本文針對一類非線性系統提出一種基于事件驅動自適應動態規劃方法的魯棒跟蹤控制方案。首先,利用系統增廣技術將原系統轉化為由跟蹤誤差和目標軌跡表示的增廣系統,從而將原系統的魯棒跟蹤問題轉化為增廣系統的魯棒鎮定問題。為了處理不確定性的同時優化系統跟蹤性能,定義了一個新的性能指標函數,進一步將增廣系統的魯棒鎮定問題轉化為其標稱系統的最優控制問題,推導得出相應的HJB方程和最優控制策略,并在理論上證明了問題轉化的等價性。針對標稱系統,提出了一個事件驅動自適應動態規劃算法設計近似最優控制策略,值得指出的是該控制策略僅在事件觸發時刻更新,可大大減少網絡負載和計算量。利用Lyapunov穩定性理論嚴格證明了閉環系統的一致最終有界穩定性。仿真例子驗證了所提出的控制方案的有效性。

1　問題描述

考慮如下的不確定非線性系統:

(1)

其中:x(t)∈Rn為系統狀態;u(t)∈Rm為系統控制輸入;d(t)∈Rm為控制擾動。假設f(x(t))和g(x(t))滿足Lipschiz連續性條件,且系統在Ω∈Rn是強可控的。本文的控制目標是設計事件驅動魯棒跟蹤控制策略u(t),使得擾動存在時系統狀態x(t)能夠跟蹤給定的目標軌跡xd(t)。假設期望軌跡滿足如下的表達式

(2)

其中:xd(t)∈Rn為有界的期望軌跡;fd(xd(t))為Lipschiz連續函數,并滿足fd(0)=0。

定義如下的跟蹤誤差

ed=x(t)-xd(t)

(3)

利用式(1)～式(3)可得系統的跟蹤誤差動態方程為

(4)

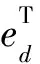
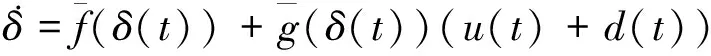
(5)

?t∈[tk,tk+1)

(6)

則當t=tk時,有ek(tk)=0。基于狀態采樣的事件驅動控制策略可表示如下

?t∈[tk,tk+1)

(7)

由式(7)可知事件驅動控制策略僅在事件觸發條件滿足時更新,而在2個相鄰的事件間則保持不變。控制輸入的連續性可由零階保持器保證。接下來,本文將針對增廣系統(5)在事件驅動控制框架下提出一個基于ADP方法的事件驅動魯棒控制策略,從而實現控制目標。

2　基于ADP的事件驅動魯棒控制

首先,通過定義一個新的性能指標函數,進一步將增廣系統的魯棒鎮定問題轉化為其標稱系統的最優控制問題,并在理論上證明問題轉化的等價性。接著,提出一個事件驅動ADP算法求解標稱系統的HJB方程,從而得到事件驅動最優控制策略。

不考慮輸入擾動,增廣系統(5)的標稱系統可以表示為

對標稱系統(5),定義一個新的性能指標函數如下:

其中:λ為衰減因子;Q和R為對稱正定常數矩陣。對上式求微分可得

(8)

定義Hamilton函數如下

H(δ,V(δ),u)=

(9)

最優性能指標函數V*(δ(t))定義如下:

(10)

根據Bellman最優控制原理可得,最優性能指標函數V*(δ(t))滿足如下的HJB方程:

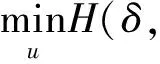
(11)

相應的最優控制策略u*(δ)為

(12)

將上式帶入式(11),可得HJB方程如下:

V*(δ)=0

(13)

定理1考慮標稱系統(6),定義性能指標函數為(7),控制策略為(12),假設跟蹤HJB方程(13)存在一個解V*(δ(t)),若不等式:

(14)

成立,則當λ=0時,閉環系統(5)漸近穩定。當λ≠0時,閉環系統(5)一致最終有界穩定。

證明選取最優性能指標函數V*(δ(t))為Lyapunov函數,對其求導可得

(15)

由HJB方程(11)可得

(16)

根據式(12)有

(17)

利用式(16)～式(17)可得

(18)

上式兩邊均乘以e-λt可得

(19)

進一步可得

(20)

對上式加減dT(t)Rd(t),并利用式(14)可得

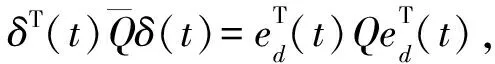
(22)

當λ≠0時,由上式可得

(23)

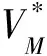
(24)

則可得閉環系統漸近穩定。證明完畢。

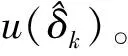
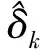
(25)

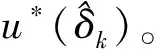
V*(δ)=W*Tσ(δ)+ε(δ)

(26)

(27)

根據式(25)和式(26)可得

(28)

(29)

將上式代入式(9)可得近似Hamilton函數:

(31)

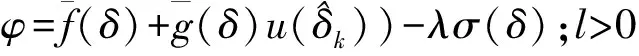
(32)

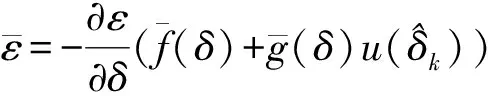
由式(6)和式(29)可得標稱系統閉環動態為

(33)

3　穩定性分析

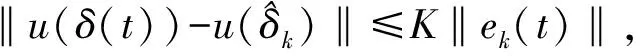
假設2g(x)有界,即‖g(x)‖≤gM,其中gM>0。

假設3評價網絡理想權值W,激活函數σ(·)及其導數σ(·),近似誤差ε及其導數ε均有界,即‖W‖≤WM,‖σ(·)‖≤σM,‖σ(·)‖≤σdM,‖ε‖≤εM,‖ε‖≤εdM,其中WM,σM,σdM,εM和εdM均為正常數。

定理2考慮系統(6),事件驅動控制策略為(29),評價網絡權值調節律為(31)。假設系統狀態滿足持續激勵條件,事件觸發條件為

(34)

其中α∈(0,1)。若評價網絡學習率l滿足如下不等式

(35)

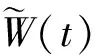
證明選取如下的Lyapunov函數

(36)

那么,當t∈[tk,tk+1)時,對Lyapunov函數(36)求導可得

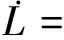
(37)

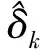
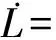
(38)

由HJB方程(13)可得

V*(δ)

(39)

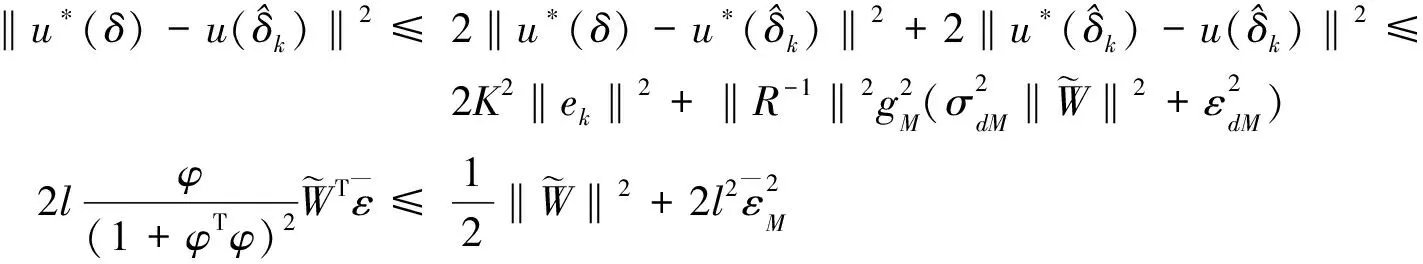
進一步可得

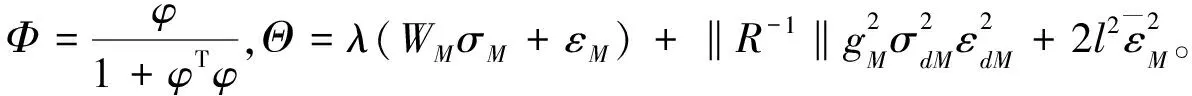
利用式(34)可得

(42)

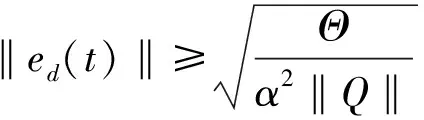
當t=tk時,對Lyapunov函數(36)求差分,

(43)

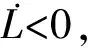
因此可得跟蹤誤差和神經網絡權值誤差均一致最終有界。證明完畢。

4　仿真例子

考慮如下的不確定非線性系統:

(44)

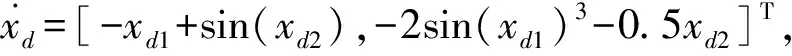
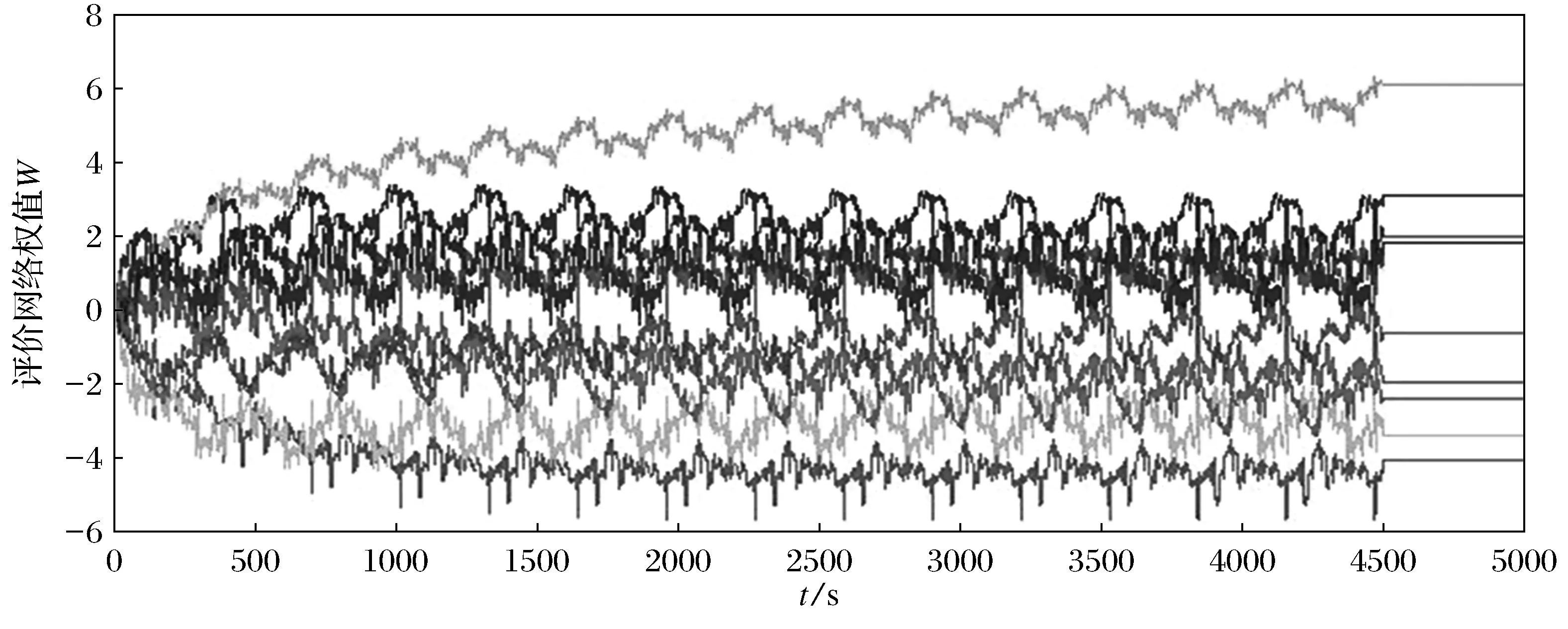
圖1　評價網絡的權值收斂軌跡Fig.1　Convergent trajectories of critic neural network weights

將所得到的事件驅動魯棒控制器作用到系統(44)上,跟蹤誤差軌跡如圖2所示,事件觸發條件ek及其上界eT的軌跡如圖3所示。本文提出的事件驅動的魯棒控制器僅需更新69次,而時間驅動的控制器則需更新500次,因此可減少86.2%的計算量。仿真結果證明了本文所提出方案的有效性。

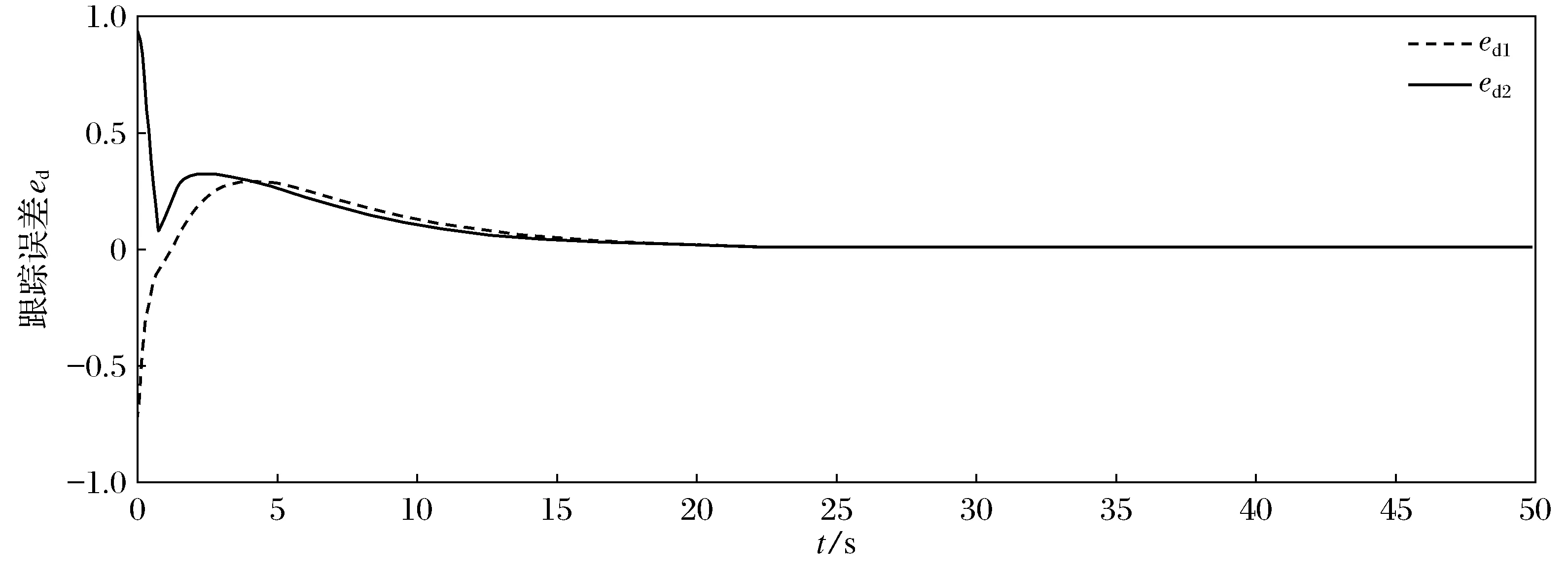
圖2　跟蹤誤差軌跡Fig.2　Trajectories of tracking error

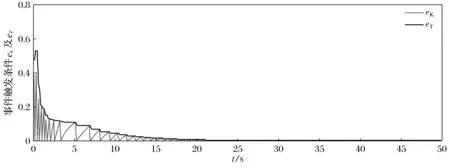
圖3　事件觸發條件軌跡Fig.3　Trajectories of event-triggered condition

5　結　　論

針對一類不確定非線性系統的魯棒跟蹤控制問題,本文利用增廣技術和引入新型性能指標函數將其轉化為標稱系統的最優控制問題,并結合事件驅動機制和ADP方法提出了一個事件驅動魯棒跟蹤控制方案,理論上證明了閉環系統的一致最終有界穩定性。仿真結果驗證了所提出方法的有效性。